第5章 特殊平行四边形 单元检测B卷(提升卷)(含解析)
文档属性
| 名称 | 第5章 特殊平行四边形 单元检测B卷(提升卷)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-17 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第5章 特殊平行四边形 单元检测B卷(提升卷)
、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.菱形的一条对角线与菱形的边相等,则它的较大的内角度数是( )
A.120° B.130° C.140° D.150°
2.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相垂直 C.对角线互相平分 D.对角线互相垂直且相等
3.如图,在正方形ABCD外侧,作等边△ADE,则∠CBE为( )
A.55° B.60° C.75° D.80°
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中不正确的是( )
A.①② B.②③ C.①③ D.②④
5.如图,矩形ABCD的对角线AC,BD相交于点O,BE⊥AC于点E,且AC=4CE,若OC=4,则矩形ABCD的面积为( )
A.12 B.20 C. D.
6.学习了正方形之后,王老师提出问题:要判断一个四边形是正方形,有哪些思路?
甲同学说:先判定四边形是菱形,再确定这个菱形对角线互相垂直;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;
丙同学说:判定四边形的对角线相等,并且互相垂直平分;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.
上述四名同学的说法中,正确的是( )
A.甲、乙 B.甲、丙 C.乙、丙、丁 D.甲、乙、丙、丁
7.在学校科技节活动中,聪聪用四根长度相同的木条制作了能够活动的菱形学具.他先活动学具成为图1所示菱形,并测得∠B=120°,接着活动学具成为图2所示正方形,并测得对角线AC=20cm,则图1中对角线AC的长为( )
A. B. C. D.
8.两张全等的矩形纸片ABCD、AECF按如图方式交叉叠放在一起.若AB=AF=2,AE=BC=8,则图中重叠(阴影)部分的面积为( )
A. B. C. D.9
9.如图,点E是正方形ABCD对角线BD上一点,点F在BC上且EF=EC,连接AE,AF,若∠ECF=α,∠AFB=β,则( )
A.β﹣α=15° B.α+β=135° C.2β﹣α=90° D.2α+β=180°
10.如图,在菱形纸片ABCD中,∠A=60°,将菱形纸片翻折,使点A落在CD的中点P处,折痕为MN,点M,N分别在边AB,AD上,则BM:AM的值为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
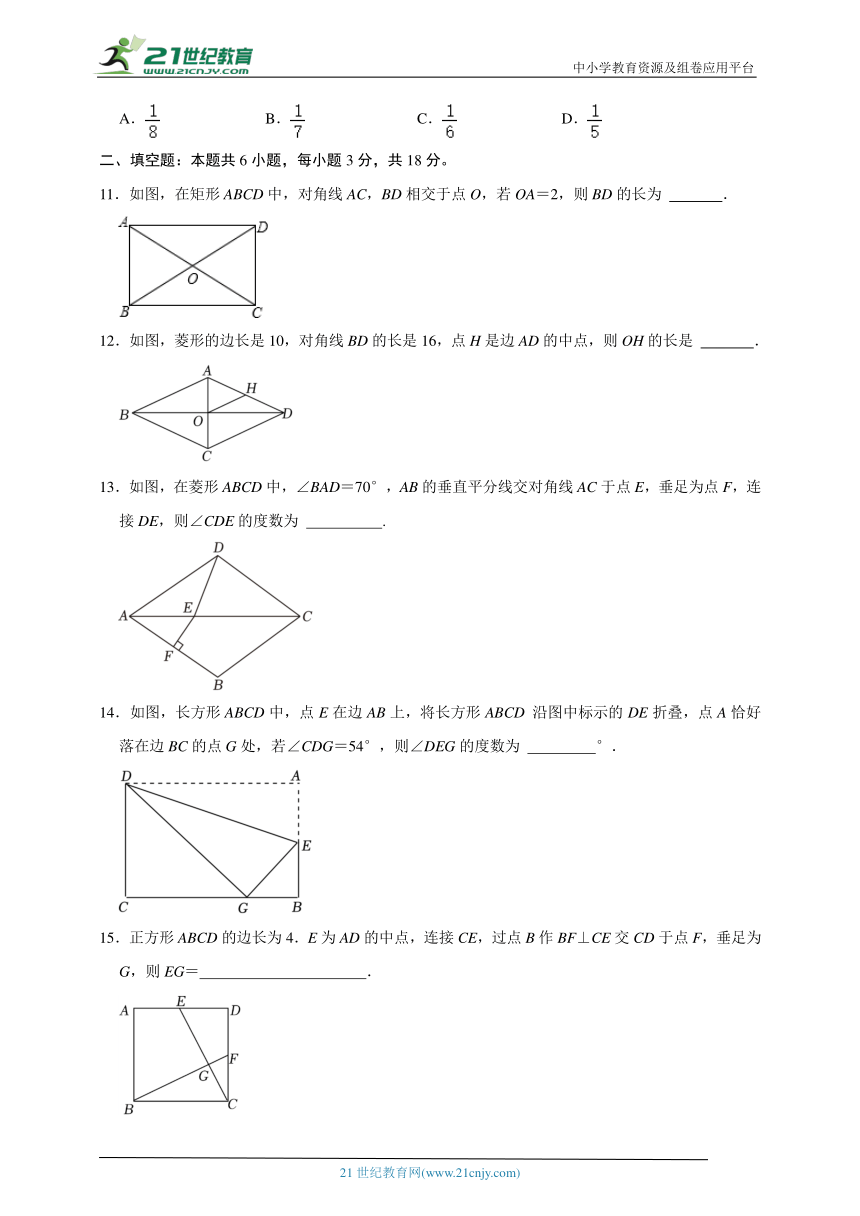
11.如图,在矩形ABCD中,对角线AC,BD相交于点O,若OA=2,则BD的长为 .
12.如图,菱形的边长是10,对角线BD的长是16,点H是边AD的中点,则OH的长是 .
13.如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点E,垂足为点F,连接DE,则∠CDE的度数为 .
14.如图,长方形ABCD中,点E在边AB上,将长方形ABCD 沿图中标示的DE折叠,点A恰好落在边BC的点G处,若∠CDG=54°,则∠DEG的度数为 °.
15.正方形ABCD的边长为4.E为AD的中点,连接CE,过点B作BF⊥CE交CD于点F,垂足为G,则EG= .
16.正方形ABCD的边长为3,点P、Q在正方形不同的边上与点A构成等腰三角形,若等腰△APQ的底边长为,则等腰△APQ的腰长是 .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,矩形ABCD的对角线AC,BD相交于点O,过点D作AC的平行线交BC的延长线于点E.
(1)求证:BD=DE;
(2)连接OE,若AB=2,BC=4,求OE的长.
18.已知:如图,在菱形ABCD中,过顶点D作DE⊥AB,DF⊥BC,垂足分别为E,F,连结EF.
(1)求证:△DEF为等腰三角形.
(2)若∠DEF=66°,求∠A的度数.
19.周末,小美和妈妈买回来一盏简单而精致的吊灯,其截面如图所示,四边形ABCD是一个菱形内框架,四边形AECF是其外部框架,且点E、B、D、F在同一直线上,BE=DF.
(1)求证:四边形外框AECF是菱形;
(2)若外框AECF的周长为80cm,EF=32cm,BE=7cm,求AB的长.
20.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AC=2AB时,四边形EGCF是矩形.
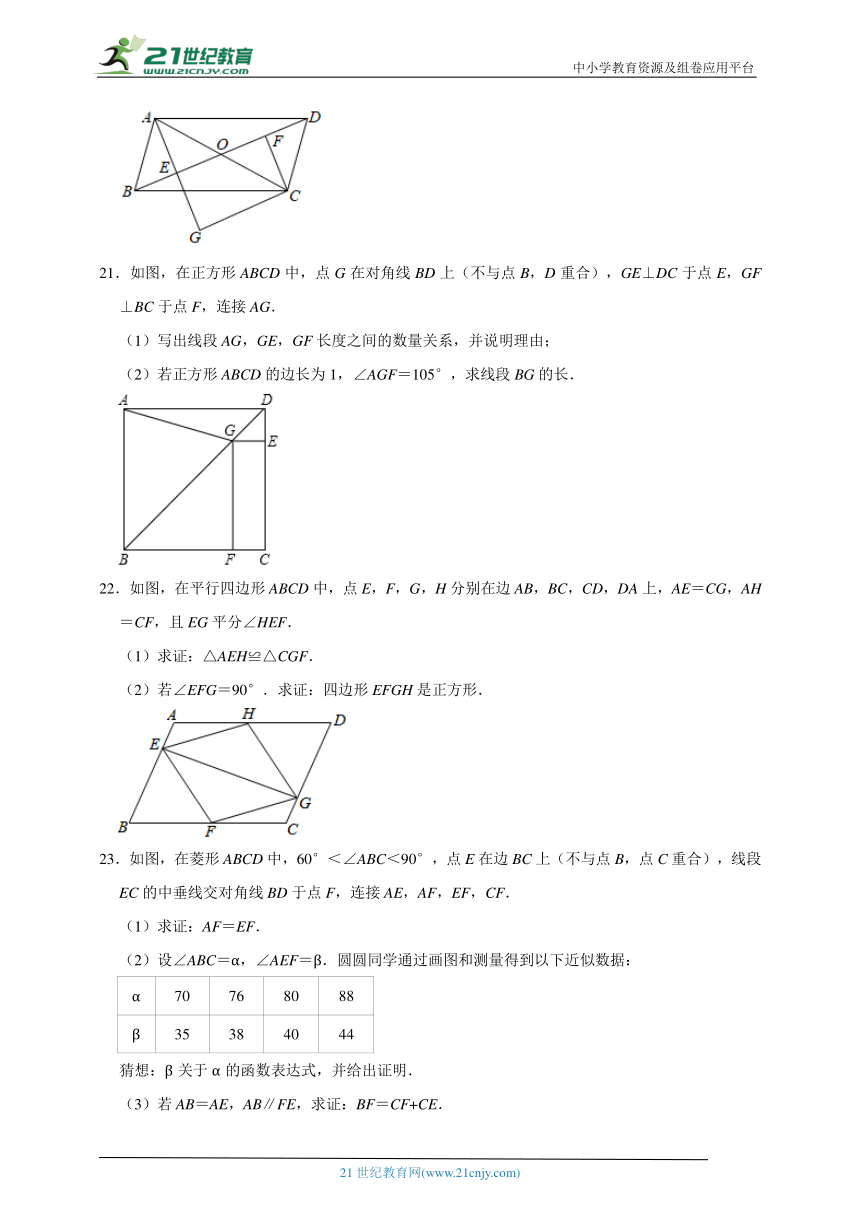
21.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
22.如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,且EG平分∠HEF.
(1)求证:△AEH≌△CGF.
(2)若∠EFG=90°.求证:四边形EFGH是正方形.
23.如图,在菱形ABCD中,60°<∠ABC<90°,点E在边BC上(不与点B,点C重合),线段EC的中垂线交对角线BD于点F,连接AE,AF,EF,CF.
(1)求证:AF=EF.
(2)设∠ABC=α,∠AEF=β.圆圆同学通过画图和测量得到以下近似数据:
α 70 76 80 88
β 35 38 40 44
猜想:β关于α的函数表达式,并给出证明.
(3)若AB=AE,AB∥FE,求证:BF=CF+CE.
24.在正方形ABCD中,点E在AD边上(不与点A,点D重合).连接BE,作AG⊥BE于点F,交CD边于点G,连接CF.
(1)求证:BE=AG.
(2)若点E是AD边的中点,AD=10.
①分别求AF,BF的长.
②求证:CB=CF.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.菱形的一条对角线与菱形的边相等,则它的较大的内角度数是( )
A.120° B.130° C.140° D.150°
【点拨】由已知可得该对角线与菱形的边长组成一个等边三角形,从而求得其一个内角为60°,则可得到较大的内角为120°.
【解析】解:因为菱形的一条对角线与边长相等,所以该对角线和菱形的两边组成的是等边三角形,可得该菱形较小内角的度数是60°,所以该菱形较大内角的度数是120°.
故选:A.
【点睛】此题主要考查菱形的性质及等边三角形的判定和性质的综合运用.
2.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相垂直 C.对角线互相平分 D.对角线互相垂直且相等
【点拨】矩形、菱形、正方形都是特殊的平行四边形,因而平行四边形的性质就是四个图形都具有的性质.
【解析】解:平行四边形的对角线互相平分,而对角线相等、平分一组对角、互相垂直不一定成立.
故平行四边形、矩形、菱形、正方形都具有的性质是:对角线互相平分.
故选:C.
【点睛】本题主要考查了正方形、矩形、菱形、平行四边形的性质,理解四个图形之间的关系是解题关键.
3.如图,在正方形ABCD外侧,作等边△ADE,则∠CBE为( )
A.55° B.60° C.75° D.80°
【点拨】先根据已知条件推出△BAE是等腰三角形,再根据等边对等角及三角形内角和定理即可求解.
【解析】解:∵在正方形ABCD外侧,作等边△ADE,
∴∠ABC=∠BAD=90°,∠DAE=60°,AB=AD=AE,
∴∠BAE=∠BAD+∠DAE=90°+60°=150°,
∴,
∴∠CBE=∠ABC﹣ABE=90°﹣15°=75°,
故选:C.
【点睛】本题考查正方形的性质,等边三角形的性质,等腰三角形的性质等,解题的关键是掌握相关知识的灵活运用.
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中不正确的是( )
A.①② B.②③ C.①③ D.②④
【点拨】要判定是正方形,则需判定它既是菱形又是矩形,据此解答.
【解析】解:A、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,
故本选项不符合题意;
B、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,
故本选项符合题意;
C、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,
故本选项不符合题意;
D、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,
故本选项不符合题意;
故选:B.
【点睛】本题考查了正方形的判定,掌握正方形的判定方法是解题的关键.
5.如图,矩形ABCD的对角线AC,BD相交于点O,BE⊥AC于点E,且AC=4CE,若OC=4,则矩形ABCD的面积为( )
A.12 B.20 C. D.
【点拨】根据矩形的性质得到BO=OD,AO=OC=4,BD=AC,求得OC=OB=4,根据勾股定理得到BE==,根据三角形的面积公式即可得到结论.
【解析】解:∵四边形ABCD是矩形,
∴BO=OD,AO=OC=4,BD=AC,
∴OC=OB=4,
∵AC=4CE,
∴OC=2CE,
∴OE=,
∵BE⊥AC,
∴BE==,
∴矩形ABCD的面积=2S△ABC=2×AC BE=2×=16.
故选:C.
【点睛】本题考查了矩形的性质,等边三角形的性质和判定,30°直角三角形性质等知识点,熟练掌握并运用等边三角形性质和判定并求出∠DBA=30°是本题解题的关键.
6.学习了正方形之后,王老师提出问题:要判断一个四边形是正方形,有哪些思路?
甲同学说:先判定四边形是菱形,再确定这个菱形对角线互相垂直;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;
丙同学说:判定四边形的对角线相等,并且互相垂直平分;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.
上述四名同学的说法中,正确的是( )
A.甲、乙 B.甲、丙 C.乙、丙、丁 D.甲、乙、丙、丁
【点拨】根据正方形的判定定理即可得到结论.
【解析】解:甲同学说:先判定四边形是菱形,再确定这个菱形对角线互相垂直,不能确定这个四边形是正方形;错误;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;正确;
丙同学说:判定四边形的对角线相等,并且互相垂直平分;正确;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等,正确;
故选:C.
【点睛】本题考查了正方形的判定定理,熟练掌握正方形的判定定理是解题的关键.
7.在学校科技节活动中,聪聪用四根长度相同的木条制作了能够活动的菱形学具.他先活动学具成为图1所示菱形,并测得∠B=120°,接着活动学具成为图2所示正方形,并测得对角线AC=20cm,则图1中对角线AC的长为( )
A. B. C. D.
【点拨】如图1中连接BD,AC,如图2中,连接AC.在图2中,利用勾股定理求出BC,在图1中,只要证明△ABC是等边三角形即可解决问题.
【解析】解:如图1中连接BD,AC,如图2中,连接AC.
在图2中,
∵四边形ABCD是正方形,
∴AB=BC,∠B=90°,
∵AC=20cm,AB2+BC2=AC2,
∴,
在图1中,∵四边形ABCD是菱形,∠B=120°,
∴AB∥DC,CD=BC,AC⊥BD,AO=CO,BO=DO,
∴∠C=60°,
∴△BCD是等边三角形,
∴,
∴,
∴,
∴,
故选:C.
【点睛】本题考查菱形的性质、正方形的性质、勾股定理等知识,解题的关键定灵活运用所学知识解决问题,属于中考常考题型.
8.两张全等的矩形纸片ABCD、AECF按如图方式交叉叠放在一起.若AB=AF=2,AE=BC=8,则图中重叠(阴影)部分的面积为( )
A. B. C. D.9
【点拨】先证四边形AGCH是平行四边形,再证△ABG≌△CEG(AAS),得AG=CG,则四边形AGCH是菱形,设AG=CG=x,则BG=BC﹣CG=8﹣x,然后在Rt△ABG中,由勾股定理得出方程,解方程得出CG的长,即可解决问题.
【解析】解:设BC交AE于G,AD交CF于H,如图所示:
∵四边形ABCD、四边形AECF是全等的矩形,
∴AB=CE,∠B=∠E=90°,AD∥BC,AE∥CF,
∴四边形AGCH是平行四边形,
在△ABG和△CEG中,
,
∴△ABG≌△CEG(AAS),
∴AG=CG,
∴四边形AGCH是菱形,
设AG=CG=x,则BG=BC﹣CG=8﹣x,
在Rt△ABG中,AB2+BG2=AG2,
∴22+(8﹣x)2=x2,
解得:x=,
∴CG=,
∴菱形AGCH的面积=CG×AB=×2=,
即图中重叠(阴影)部分的面积为,
故选:C.
【点睛】本题考查了菱形的判定与性质、矩形的性质、全等图形的性质、平行四边形的判定与性质、全等三角形的判定与性质、勾股定理等知识;熟练掌握菱形的判定与性质,由勾股定理求出CG的长是解题的关键.
9.如图,点E是正方形ABCD对角线BD上一点,点F在BC上且EF=EC,连接AE,AF,若∠ECF=α,∠AFB=β,则( )
A.β﹣α=15° B.α+β=135° C.2β﹣α=90° D.2α+β=180°
【点拨】根据正方形的性质得到AB=BC,∠ABE=∠CBE=45°,根据全等三角形的性质得到AE=CE,∠BCE=∠BAE=α,根据等腰三角形的性质得到∠EFC=∠ECF=α,求得∠AFE=180°﹣α﹣β,根据等腰三角形的性质列方程即可得到结论.
【解析】解:∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠CBE=45°,
∵BE=BE,
∴△ABE≌△CBE(SAS),
∴AE=CE,∠BCE=∠BAE=α,
∵EF=CE,
∴∠EFC=∠ECF=α,
∵∠AFB=β,
∴∠AFE=180°﹣α﹣β,
∵∠ABF=90°,
∴∠BAF=90°﹣β,
∵AE=CE,EF=CE,
∴AE=EF,
∴∠EAF=∠AFE,
∴α﹣(90°﹣β)=180°﹣α﹣β,
∴α+β=135°,
故选:B.
【点睛】本题考查了正方形的性质,全等三角形的判定和性质,等腰三角形的性质,三角形内角和定理,熟练掌握正方形的性质是解题的关键.
10.如图,在菱形纸片ABCD中,∠A=60°,将菱形纸片翻折,使点A落在CD的中点P处,折痕为MN,点M,N分别在边AB,AD上,则BM:AM的值为( )
A. B. C. D.
【点拨】由菱形的性质和等边三角形的性质,可得BP⊥CD,DP=a,∠DBP=30°,由勾股定理可求解.
【解析】解:如图,连接BD,BP,
设AB=2a,
∵四边形ABCD是菱形,∠A=60°,
∴AB=BC=2a=CD,∠A=∠C=60°,
∴△BCD是等边三角形,△ABD是等边三角形,
∵点P在CD的中点,
∴BP⊥CD,DP=a,∠DBP=30°,
∴BP=a,∠ABP=∠ABD+∠DBP=90°,
∵将菱形纸片翻折,
∴AM=MP,
∵MP2=MB2+BP2,
∴(2a﹣BM)2=MB2+3a2,
∴BM=a,
∴AM=a,
∴BM:AM=,
故选:B.
【点睛】本题考查了翻折变换,等边三角形的性质,菱形的性质,勾股定理,添加恰当的辅助线构造直角三角形是本题的关键.
二、填空题:本题共6小题,每小题3分,共18分。
11.如图,在矩形ABCD中,对角线AC,BD相交于点O,若OA=2,则BD的长为 4 .
【点拨】因为矩形的对角线相等且互相平分,已知OA=2,则AC=2OA=4,又BD=AC,故可求.
【解析】解:∵ABCD是矩形
∴OC=OA,BD=AC
又∵OA=2,
∴AC=OA+OC=2OA=4
∴BD=AC=4
故答案为:4.
【点睛】本题考查矩形的对角线相等的性质,属于矩形的基本性质,比较简单.
12.如图,菱形的边长是10,对角线BD的长是16,点H是边AD的中点,则OH的长是 5 .
【点拨】根据菱形的性质可得OB=OD,AO⊥BO,从而可判断OH是△ABD的中位线.
【解析】解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AO=OC,OB=OD,AO⊥BO,
∵AB=10,
又∵点H是AD中点,
∴OH是△DAB的中位线,
∴OH=AB=5.
故答案为:5.
【点睛】本题考查了菱形的性质及三角形的中位线定理,熟练掌握菱形四边相等、对角线互相垂直且平分的性质是解题关键.
13.如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点E,垂足为点F,连接DE,则∠CDE的度数为 75° .
【点拨】连接BE,根据菱形的对角线平分一组对角线可得∠BAC=35°,根据线段垂直平分线上的点到两端点的距离相等可得AE=BE,根据等边对等角可得∠ABE=∠BAC,再根据菱形的邻角互补求出∠ABC,然后求出∠CBE,最后根据菱形的对称性可得∠CDE=∠CBE.
【解析】解:如图,连接BE,
在菱形ABCD中,∠BAC=∠BAD=×70°=35°,
∵EF是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠BAC=35°,
∵菱形ABCD的对边AD∥BC,
∴∠ABC=180°﹣∠BAD=180°﹣70°=110°,
∴∠CBE=∠ABC﹣∠ABE=110°﹣35°=75°,
由菱形的对称性,∠CDE=∠CBE=75°.
故答案为:75°.
【点睛】本题考查了菱形的性质,线段垂直平分线上的点到两端点的距离相等的性质,等边对等角的性质,熟记各性质是解题的关键.
14.如图,长方形ABCD中,点E在边AB上,将长方形ABCD 沿图中标示的DE折叠,点A恰好落在边BC的点G处,若∠CDG=54°,则∠DEG的度数为 72 °.
【点拨】由矩形的性质得∠A=∠ADC=∠C=90°,AD∥BC,则∠ADG=∠CGD=90°﹣∠CDG=36°,由折叠得∠DGE=∠A=90°,∠GDE=∠ADE=∠ADG=18°,则∠DEG=90°﹣∠GDE=72°,于是得到问题的答案.
【解析】解:∵四边形ABCD是矩形,
∴∠A=∠ADC=∠C=90°,AD∥BC,
∵∠CDG=54°,
∴∠CGD=90°﹣∠CDG=90°﹣54°=36°,
∴∠ADG=∠CGD=36°,
∵将长方形ABCD 沿DE折叠,点A落在边BC的点G处,
∴∠DGE=∠A=90°,∠GDE=∠ADE=∠ADG=×36°=18°,
∴∠DEG=90°﹣∠GDE=90°﹣18°=72°,
故答案为:72.
【点睛】此题重点考查矩形的性质、轴对称的性质、平行线的性质、直角三角形的两个锐角互余等知识,求得∠ADG=∠CGD=36°是解题的关键.
15.正方形ABCD的边长为4.E为AD的中点,连接CE,过点B作BF⊥CE交CD于点F,垂足为G,则EG= .
【点拨】利用勾股定理可求BF的长,由面积法可求EG.
【解析】解:∵四边形ABCD是正方形,
∴AD=CD=BC,∠BCD=∠ADC=90°,
∴∠DCE+∠DEC=90°,
∵BF⊥CE,
∴∠DCE+∠CFB=90°,
∴∠BFC=∠DEC,
∴△BFC≌△CED(AAS),
∴DE=CF=2,CE=BF,
∴BF=,
∴CE=2,
∵S△BFC=×BC×CF=×BF×CG,
∴4×2=2CG,
∴CG=,
∴EG=,
故答案为:.
【点睛】考查了正方形的性质,全等三角形的判定和性质,勾股定理等知识,添加恰当辅助线构造全等三角形是解题的关键.
16.正方形ABCD的边长为3,点P、Q在正方形不同的边上与点A构成等腰三角形,若等腰△APQ的底边长为,则等腰△APQ的腰长是 2或或 .
【点拨】分三种情况进行讨论,当P、Q分别在AD、AB上,AP=AQ,当P、Q分别在CD、BD上,AP=AQ,当AP=PQ,点P在CD上,点Q在AB上,分别画出图形,根据正方形的性质和勾股定理进行求解即可.
【解析】解:当P、Q分别在AD、AB上,AP=AQ,△APQ为等腰直角三角形,如图所示:
∵,
∴;
当P、Q分别在CD、BD上,AP=AQ,如图所示:
∵四边形ABCD为正方形,
∴AB=AC=BD=CD=3,∠B=∠C=90°,
∴Rt△ABQ≌Rt△ACP,
∴BQ=CP,
∴BD﹣BQ=CD﹣CP,即DP=DQ,
∴△DPQ为等腰直角三角形,
∵,
∴,
∴BQ=3﹣2=1,
∴此时腰长为;
当AP=PQ,点P在CD上,点Q在AB上,过点P作PM⊥AB于点M,如图所示:
∵AP=PQ,PM⊥AB,,
∴,
∵∠AMP=∠CAM=∠C=90°,
∴四边形AMPC为矩形,
∴MP=AC=3,
∴.
综上分析可知:等腰△APQ的腰长是2或或.
故答案为:2或或.
【点睛】本题主要考查了等腰三角形的判定和性质,正方形的性质,勾股定理,矩形的判定和性质,解题的关键是数形结合,熟练掌握相关的判定和性质.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,矩形ABCD的对角线AC,BD相交于点O,过点D作AC的平行线交BC的延长线于点E.
(1)求证:BD=DE;
(2)连接OE,若AB=2,BC=4,求OE的长.
【点拨】(1)根据矩形的对角线相等可得AC=BD,对边平行可得AB∥CD,再求出四边形ABEC是平行四边形,根据平行四边形的对边相等可得AC=BE,从而得证;
(2)如图,过点O作OF⊥CD于点F,欲求OE,只需在直角△OEF中求得OF、FE的值即可.OF结合三角形中位线求得EF,结合矩形、平行四边形的性质以及勾股定理求得即可.
【解析】(1)证明:在矩形ABCD中,AD∥BC,AD=BC,
∴AD∥CE.
∵Ac∥DE.
∴四边形ACED是平行四边形.
∴AC=DE.
在矩形ABCD中,AC=BD,
∴BD=DE
(2)解:作OH⊥BE于H,如图.
在矩形ABCD中,AC=BD,且AC与BD交于点O,
∴OB=OC=OA.
∴BH=HC. ,
∵AB=2,BC=4,
∴OH=1,HC=2.
在平行四边形ACED中,AD=CE.
∴CE=BC=4.
∴HE=6.
在Rt△OHE中,OE=.
【点睛】本题考查了矩形的性质,平行四边形的判定与性质,熟记各性质并求出四边形ABEC是平行四边形是解题的关键.
18.已知:如图,在菱形ABCD中,过顶点D作DE⊥AB,DF⊥BC,垂足分别为E,F,连结EF.
(1)求证:△DEF为等腰三角形.
(2)若∠DEF=66°,求∠A的度数.
【点拨】(1)利用菱形的性质得到AD=CD,∠A=∠C,进而利用AAS证明两三角形全等,进而利用全等三角形的性质和等腰三角形的判定解答即可;
(2)求出∠DEF=∠DFE=66°,由菱形的性质可得出答案.
【解析】(1)证明:∵四边形ABCD是菱形,
∴AD=CD,∠A=∠C,
∵DE⊥BA,DF⊥CB,
∴∠AED=∠CFD=90°,
在△ADE和△CDF,
,
∴△ADE≌△CDF(AAS),
∴DE=DF,
∴△DEF是等腰三角形;
(2)解:∵DE=DF,
∴∠DEF=∠DFE=66°,
∴∠BEF=∠BFE=90°﹣66°=24°,
∴∠B=180°﹣24°﹣24°=132°,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠A=180°﹣∠B=48°.
【点睛】本题主要考查了菱形的性质以及全等三角形的判定与性质,解题的关键是掌握菱形的性质以及AAS证明两三角形全等,此题难度一般.
19.周末,小美和妈妈买回来一盏简单而精致的吊灯,其截面如图所示,四边形ABCD是一个菱形内框架,四边形AECF是其外部框架,且点E、B、D、F在同一直线上,BE=DF.
(1)求证:四边形外框AECF是菱形;
(2)若外框AECF的周长为80cm,EF=32cm,BE=7cm,求AB的长.
【点拨】(1)根据菱形的性质和全等三角形的判定和性质得出AE=AF=CE=CF,进而利用菱形的判定解答即可;
(2)根据菱形的性质和勾股定理得出AC,进而解答即可.
【解析】(1)证明:∵四边形ABCD是菱形,
∴AB=AD=BC=CD,∠ABD=∠CBD=∠ADB=∠CDB,
∴∠ABE=∠ADF,
在△ABE与△ADF中,
,
∴△ABE≌△ADF(SAS),
∴AE=AF,
同理可得:AE=CE=CF=AF,
∴四边形AECF是菱形;
(2)解:连接AC,交EF于点O,
∵四边形AECF是菱形,外框AECF的周长为80cm,
∴AE=20cm,EF⊥AC,OE=OF,
∵EF=32cm,BE=7cm,
∴OE=16cm,OB=16﹣7=9(cm),
∴OA=(cm),
∴AB=(cm).
【点睛】此题考查菱形的判定和性质,关键是根据四条边相等的四边形是菱形解答.
20.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AC=2AB时,四边形EGCF是矩形.
【点拨】(1)由平行四边形的性质得出AB=CD,AB∥CD,OB=OD,OA=OC,由平行线的性质得出∠ABE=∠CDF,证出BE=DF,由SAS证明△ABE≌△CDF即可;
(2)证出AB=OA,由等腰三角形的性质得出AG⊥OB,∠OEG=90°,同理:CF⊥OD,得出EG∥CF,由三角形中位线定理得出OE∥CG,EF∥CG,得出四边形EGCF是平行四边形,即可得出结论.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)证明:∵AC=2OA,AC=2AB,
∴AB=OA,
∵E是OB的中点,
∴AG⊥OB,
∴∠OEG=90°,
同理:CF⊥OD,
∴AG∥CF,
∴EG∥CF,
∵EG=AE,OA=OC,
∴OE是△ACG的中位线,
∴OE∥CG,
∴EF∥CG,
∴四边形EGCF是平行四边形,
∵∠OEG=90°,
∴四边形EGCF是矩形.
【点睛】本题考查了矩形的判定、平行四边形的性质和判定、全等三角形的判定、三角形中位线定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
21.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
【点拨】(1)结论:AG2=GE2+GF2.只要证明GA=GC,四边形EGFC是矩形,推出GE=CF,在Rt△GFC中,利用勾股定理即可证明;
(2)过点A作AH⊥BG,在Rt△ABH、Rt△AHG中,求出AH、HG即可解决问题.
【解析】解:(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2.
(2)过点A作AH⊥BG,
∵四边形ABCD是正方形,
∴∠ABD=∠GBF=45°,
∵GF⊥BC,
∴∠BGF=45°,
∵∠AGF=105°,
∴∠AGB=∠AGF﹣∠BGF=105°﹣45°=60°,
在Rt△ABH中,∵AB=1,
∴AH=BH=,
在Rt△AGH中,∵AH=,∠GAH=30°,
∴HG=AH tan30°=,
∴BG=BH+HG=+.
解法二:如图,过点B作BN⊥AG于N,在BN上截取BM,使得BM=AM,设AN=x.
∵∠AGF=105°,∠GBF=∠FGB=∠ABG=45°,
∴∠AGB=60°,∠GBN=30°,∠ABM=∠BAM=15°,
∴∠AMN=∠ABM+∠BAM=30°,
∴AM=BM=2x,MN=x,
在Rt△ABN中,则有1=x2+(2x+x)2,
解得x=,
∴BN=,
∴BG==.
【点睛】本题考查正方形的性质、矩形的判定和性质、勾股定理直角三角形30度的性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
22.如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,且EG平分∠HEF.
(1)求证:△AEH≌△CGF.
(2)若∠EFG=90°.求证:四边形EFGH是正方形.
【点拨】(1)根据全等三角形的判定定理SAS证得结论;
(2)先证明四边形EFGH是平行四边形,再证明有一组邻边相等,然后结合∠EFG=90°,即可证得该平行四边形是正方形.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴∠A=∠C.
在△AEH与△CGF中,
,
∴△AEH≌△CGF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠B=∠D.
∵AE=CG,AH=CF,
∴EB=DG,HD=BF.
∴△BEF≌△DGH(SAS),
∴EF=HG.
又∵△AEH≌△CGF,
∴EH=GF.
∴四边形HEFG为平行四边形.
∴EH∥FG,
∴∠HEG=∠FGE.
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠FGE=∠FEG,
∴EF=GF,
∴平行四边形EFGH是菱形,
又∵∠EFG=90°,
∴菱形EFGH是正方形.
∴四边形EFGH是正方形.
【点睛】本题考查了正方形的判定,判定一个四边形是正方形的方法有:
①先判定四边形是矩形,再判定这个矩形有一组邻边相等;
②先判定四边形是菱形,再判定这个菱形有一个角为直角.
③还可以先判定四边形是平行四边形,再用1或2进行判定.
也考查了平行四边形的性质,全等三角形的判定与性质,难度适中.
23.如图,在菱形ABCD中,60°<∠ABC<90°,点E在边BC上(不与点B,点C重合),线段EC的中垂线交对角线BD于点F,连接AE,AF,EF,CF.
(1)求证:AF=EF.
(2)设∠ABC=α,∠AEF=β.圆圆同学通过画图和测量得到以下近似数据:
α 70 76 80 88
β 35 38 40 44
猜想:β关于α的函数表达式,并给出证明.
(3)若AB=AE,AB∥FE,求证:BF=CF+CE.
【点拨】(1)根据菱形的性质证明△ABF≌△CBF(SAS),根据题意线段EC的中垂线交BD于点F,即可得证.
(2)利用全等三角形的性质得出∠BAF=∠BCF,根据平角的定义,即可得证.
(3)求出β的度数,进而证得BF=BC,BE=EF,即可得证.
【解析】(1)证明:∵菱形ABCD,
∵∠ABD=∠CBD,AB=CB,
∵BF=BF,
∴△ABF≌△CBF(SAS),
∴AF=CF,
又∵线段EC的中垂线交BD于点F,
∴EF=CF,
∴AF=FE.
(2)猜想:α=2β.
证明:因为△ABF≌△CBF,
∴∠BAF=∠BCF,
∵EF=CF,
∴∠FEC=∠ECF,
∵∠FEC+∠FEB=180°,
∴∠BAF+∠FEB=180°,
∴∠ABC+∠AFE=180°,
即∠AFE=180°﹣a,
∵AF=FE,
∴,
∴α=2β.
(3)∵AB=AE,
∴∠ABE=∠AEB=2β,
∵AB∥FE,
∴∠FEC=∠ABE=2β,
∴∠FEC=∠ABE=∠AEB=∠ECF=2β,
∵∠AEB+∠ECF+∠AEF=180°,
∴β=36°,
∴∠BFC=72°,∠BFE=36°,
∵∠BFC=∠BCF=72°,
∴BF=BC,
∵∠BFE=∠FBC=36°,
∴BE=EF,
∴BF=BC=BE+CE=CF+CE.
【点睛】本题考查了四边形的综合应用,解题的关键是掌握菱形的性质,全等三角形的性质与判定.
24.在正方形ABCD中,点E在AD边上(不与点A,点D重合).连接BE,作AG⊥BE于点F,交CD边于点G,连接CF.
(1)求证:BE=AG.
(2)若点E是AD边的中点,AD=10.
①分别求AF,BF的长.
②求证:CB=CF.
【点拨】(1)根据正方形的性质及垂线的性质得出∠ABE=∠DAG,然后利用ASA得出△ABE≌△DAG,即可得解;
(2)①利用勾股定理得出BE的长,再利用面积法求解,求解即可;
②过点C作CH⊥BF于点H,先得出∠ABF=∠BCH,∠BFA=∠CHB,再得出△ABF≌△BCH,最后利用FH=BF﹣BH求解即可.
【解析】(1)证明:∵四边形ABCD是正方形,
∴∠BAE=∠ADG=90°,AB=DA,
∴∠ABE+∠AEB=90°,
∵AG⊥BE,
∴∠AFE=90°,
∴∠DAG+∠AEB=90°,
∴∠ABE=∠DAG,
在△ABE和△DAG中,
,
∴△ABE≌△DAG(ASA),
∴BE=AG;
(2)①解:∵正方形ABCD是正方形,AD=10,
∴AB=BC=AD=10,
∴AE=AD==5,
在Rt△ABE中,由勾股定理可得:
BE=,
∵ BE AF= AB AE.
∴AF=2,BF==4,
∴AF的长为2,BF的长为4.
②如图,过点C作CH⊥BF于点H,则∠CHB=90°,
∵∠CHB=90°,
∴∠CBH+∠BCH=90°,
∵∠ABC=∠ABF+∠CBH=90°,
∴∠ABF=∠BCH,
∵∠BFA=90°,
∴∠BFA=∠CHB,
在△ABF和△BCH中,
,
∴△ABF≌△BCH(AAS),
∴AF=BH=2,
∵BF=4,
∴FH=BF﹣BH=4﹣2=2,
∴BH=FH=2,
∵CH⊥BF,
∴CH是线段BF的垂直平分线,
∴CB=CF.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,勾股定理的运用,正确作出辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第5章 特殊平行四边形 单元检测B卷(提升卷)
、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.菱形的一条对角线与菱形的边相等,则它的较大的内角度数是( )
A.120° B.130° C.140° D.150°
2.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相垂直 C.对角线互相平分 D.对角线互相垂直且相等
3.如图,在正方形ABCD外侧,作等边△ADE,则∠CBE为( )
A.55° B.60° C.75° D.80°
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中不正确的是( )
A.①② B.②③ C.①③ D.②④
5.如图,矩形ABCD的对角线AC,BD相交于点O,BE⊥AC于点E,且AC=4CE,若OC=4,则矩形ABCD的面积为( )
A.12 B.20 C. D.
6.学习了正方形之后,王老师提出问题:要判断一个四边形是正方形,有哪些思路?
甲同学说:先判定四边形是菱形,再确定这个菱形对角线互相垂直;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;
丙同学说:判定四边形的对角线相等,并且互相垂直平分;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.
上述四名同学的说法中,正确的是( )
A.甲、乙 B.甲、丙 C.乙、丙、丁 D.甲、乙、丙、丁
7.在学校科技节活动中,聪聪用四根长度相同的木条制作了能够活动的菱形学具.他先活动学具成为图1所示菱形,并测得∠B=120°,接着活动学具成为图2所示正方形,并测得对角线AC=20cm,则图1中对角线AC的长为( )
A. B. C. D.
8.两张全等的矩形纸片ABCD、AECF按如图方式交叉叠放在一起.若AB=AF=2,AE=BC=8,则图中重叠(阴影)部分的面积为( )
A. B. C. D.9
9.如图,点E是正方形ABCD对角线BD上一点,点F在BC上且EF=EC,连接AE,AF,若∠ECF=α,∠AFB=β,则( )
A.β﹣α=15° B.α+β=135° C.2β﹣α=90° D.2α+β=180°
10.如图,在菱形纸片ABCD中,∠A=60°,将菱形纸片翻折,使点A落在CD的中点P处,折痕为MN,点M,N分别在边AB,AD上,则BM:AM的值为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.如图,在矩形ABCD中,对角线AC,BD相交于点O,若OA=2,则BD的长为 .
12.如图,菱形的边长是10,对角线BD的长是16,点H是边AD的中点,则OH的长是 .
13.如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点E,垂足为点F,连接DE,则∠CDE的度数为 .
14.如图,长方形ABCD中,点E在边AB上,将长方形ABCD 沿图中标示的DE折叠,点A恰好落在边BC的点G处,若∠CDG=54°,则∠DEG的度数为 °.
15.正方形ABCD的边长为4.E为AD的中点,连接CE,过点B作BF⊥CE交CD于点F,垂足为G,则EG= .
16.正方形ABCD的边长为3,点P、Q在正方形不同的边上与点A构成等腰三角形,若等腰△APQ的底边长为,则等腰△APQ的腰长是 .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,矩形ABCD的对角线AC,BD相交于点O,过点D作AC的平行线交BC的延长线于点E.
(1)求证:BD=DE;
(2)连接OE,若AB=2,BC=4,求OE的长.
18.已知:如图,在菱形ABCD中,过顶点D作DE⊥AB,DF⊥BC,垂足分别为E,F,连结EF.
(1)求证:△DEF为等腰三角形.
(2)若∠DEF=66°,求∠A的度数.
19.周末,小美和妈妈买回来一盏简单而精致的吊灯,其截面如图所示,四边形ABCD是一个菱形内框架,四边形AECF是其外部框架,且点E、B、D、F在同一直线上,BE=DF.
(1)求证:四边形外框AECF是菱形;
(2)若外框AECF的周长为80cm,EF=32cm,BE=7cm,求AB的长.
20.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AC=2AB时,四边形EGCF是矩形.
21.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
22.如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,且EG平分∠HEF.
(1)求证:△AEH≌△CGF.
(2)若∠EFG=90°.求证:四边形EFGH是正方形.
23.如图,在菱形ABCD中,60°<∠ABC<90°,点E在边BC上(不与点B,点C重合),线段EC的中垂线交对角线BD于点F,连接AE,AF,EF,CF.
(1)求证:AF=EF.
(2)设∠ABC=α,∠AEF=β.圆圆同学通过画图和测量得到以下近似数据:
α 70 76 80 88
β 35 38 40 44
猜想:β关于α的函数表达式,并给出证明.
(3)若AB=AE,AB∥FE,求证:BF=CF+CE.
24.在正方形ABCD中,点E在AD边上(不与点A,点D重合).连接BE,作AG⊥BE于点F,交CD边于点G,连接CF.
(1)求证:BE=AG.
(2)若点E是AD边的中点,AD=10.
①分别求AF,BF的长.
②求证:CB=CF.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.菱形的一条对角线与菱形的边相等,则它的较大的内角度数是( )
A.120° B.130° C.140° D.150°
【点拨】由已知可得该对角线与菱形的边长组成一个等边三角形,从而求得其一个内角为60°,则可得到较大的内角为120°.
【解析】解:因为菱形的一条对角线与边长相等,所以该对角线和菱形的两边组成的是等边三角形,可得该菱形较小内角的度数是60°,所以该菱形较大内角的度数是120°.
故选:A.
【点睛】此题主要考查菱形的性质及等边三角形的判定和性质的综合运用.
2.平行四边形、矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相垂直 C.对角线互相平分 D.对角线互相垂直且相等
【点拨】矩形、菱形、正方形都是特殊的平行四边形,因而平行四边形的性质就是四个图形都具有的性质.
【解析】解:平行四边形的对角线互相平分,而对角线相等、平分一组对角、互相垂直不一定成立.
故平行四边形、矩形、菱形、正方形都具有的性质是:对角线互相平分.
故选:C.
【点睛】本题主要考查了正方形、矩形、菱形、平行四边形的性质,理解四个图形之间的关系是解题关键.
3.如图,在正方形ABCD外侧,作等边△ADE,则∠CBE为( )
A.55° B.60° C.75° D.80°
【点拨】先根据已知条件推出△BAE是等腰三角形,再根据等边对等角及三角形内角和定理即可求解.
【解析】解:∵在正方形ABCD外侧,作等边△ADE,
∴∠ABC=∠BAD=90°,∠DAE=60°,AB=AD=AE,
∴∠BAE=∠BAD+∠DAE=90°+60°=150°,
∴,
∴∠CBE=∠ABC﹣ABE=90°﹣15°=75°,
故选:C.
【点睛】本题考查正方形的性质,等边三角形的性质,等腰三角形的性质等,解题的关键是掌握相关知识的灵活运用.
4.已知四边形ABCD是平行四边形,再从①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中不正确的是( )
A.①② B.②③ C.①③ D.②④
【点拨】要判定是正方形,则需判定它既是菱形又是矩形,据此解答.
【解析】解:A、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,
故本选项不符合题意;
B、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,
故本选项符合题意;
C、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,
故本选项不符合题意;
D、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,
故本选项不符合题意;
故选:B.
【点睛】本题考查了正方形的判定,掌握正方形的判定方法是解题的关键.
5.如图,矩形ABCD的对角线AC,BD相交于点O,BE⊥AC于点E,且AC=4CE,若OC=4,则矩形ABCD的面积为( )
A.12 B.20 C. D.
【点拨】根据矩形的性质得到BO=OD,AO=OC=4,BD=AC,求得OC=OB=4,根据勾股定理得到BE==,根据三角形的面积公式即可得到结论.
【解析】解:∵四边形ABCD是矩形,
∴BO=OD,AO=OC=4,BD=AC,
∴OC=OB=4,
∵AC=4CE,
∴OC=2CE,
∴OE=,
∵BE⊥AC,
∴BE==,
∴矩形ABCD的面积=2S△ABC=2×AC BE=2×=16.
故选:C.
【点睛】本题考查了矩形的性质,等边三角形的性质和判定,30°直角三角形性质等知识点,熟练掌握并运用等边三角形性质和判定并求出∠DBA=30°是本题解题的关键.
6.学习了正方形之后,王老师提出问题:要判断一个四边形是正方形,有哪些思路?
甲同学说:先判定四边形是菱形,再确定这个菱形对角线互相垂直;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;
丙同学说:判定四边形的对角线相等,并且互相垂直平分;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.
上述四名同学的说法中,正确的是( )
A.甲、乙 B.甲、丙 C.乙、丙、丁 D.甲、乙、丙、丁
【点拨】根据正方形的判定定理即可得到结论.
【解析】解:甲同学说:先判定四边形是菱形,再确定这个菱形对角线互相垂直,不能确定这个四边形是正方形;错误;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;正确;
丙同学说:判定四边形的对角线相等,并且互相垂直平分;正确;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等,正确;
故选:C.
【点睛】本题考查了正方形的判定定理,熟练掌握正方形的判定定理是解题的关键.
7.在学校科技节活动中,聪聪用四根长度相同的木条制作了能够活动的菱形学具.他先活动学具成为图1所示菱形,并测得∠B=120°,接着活动学具成为图2所示正方形,并测得对角线AC=20cm,则图1中对角线AC的长为( )
A. B. C. D.
【点拨】如图1中连接BD,AC,如图2中,连接AC.在图2中,利用勾股定理求出BC,在图1中,只要证明△ABC是等边三角形即可解决问题.
【解析】解:如图1中连接BD,AC,如图2中,连接AC.
在图2中,
∵四边形ABCD是正方形,
∴AB=BC,∠B=90°,
∵AC=20cm,AB2+BC2=AC2,
∴,
在图1中,∵四边形ABCD是菱形,∠B=120°,
∴AB∥DC,CD=BC,AC⊥BD,AO=CO,BO=DO,
∴∠C=60°,
∴△BCD是等边三角形,
∴,
∴,
∴,
∴,
故选:C.
【点睛】本题考查菱形的性质、正方形的性质、勾股定理等知识,解题的关键定灵活运用所学知识解决问题,属于中考常考题型.
8.两张全等的矩形纸片ABCD、AECF按如图方式交叉叠放在一起.若AB=AF=2,AE=BC=8,则图中重叠(阴影)部分的面积为( )
A. B. C. D.9
【点拨】先证四边形AGCH是平行四边形,再证△ABG≌△CEG(AAS),得AG=CG,则四边形AGCH是菱形,设AG=CG=x,则BG=BC﹣CG=8﹣x,然后在Rt△ABG中,由勾股定理得出方程,解方程得出CG的长,即可解决问题.
【解析】解:设BC交AE于G,AD交CF于H,如图所示:
∵四边形ABCD、四边形AECF是全等的矩形,
∴AB=CE,∠B=∠E=90°,AD∥BC,AE∥CF,
∴四边形AGCH是平行四边形,
在△ABG和△CEG中,
,
∴△ABG≌△CEG(AAS),
∴AG=CG,
∴四边形AGCH是菱形,
设AG=CG=x,则BG=BC﹣CG=8﹣x,
在Rt△ABG中,AB2+BG2=AG2,
∴22+(8﹣x)2=x2,
解得:x=,
∴CG=,
∴菱形AGCH的面积=CG×AB=×2=,
即图中重叠(阴影)部分的面积为,
故选:C.
【点睛】本题考查了菱形的判定与性质、矩形的性质、全等图形的性质、平行四边形的判定与性质、全等三角形的判定与性质、勾股定理等知识;熟练掌握菱形的判定与性质,由勾股定理求出CG的长是解题的关键.
9.如图,点E是正方形ABCD对角线BD上一点,点F在BC上且EF=EC,连接AE,AF,若∠ECF=α,∠AFB=β,则( )
A.β﹣α=15° B.α+β=135° C.2β﹣α=90° D.2α+β=180°
【点拨】根据正方形的性质得到AB=BC,∠ABE=∠CBE=45°,根据全等三角形的性质得到AE=CE,∠BCE=∠BAE=α,根据等腰三角形的性质得到∠EFC=∠ECF=α,求得∠AFE=180°﹣α﹣β,根据等腰三角形的性质列方程即可得到结论.
【解析】解:∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠CBE=45°,
∵BE=BE,
∴△ABE≌△CBE(SAS),
∴AE=CE,∠BCE=∠BAE=α,
∵EF=CE,
∴∠EFC=∠ECF=α,
∵∠AFB=β,
∴∠AFE=180°﹣α﹣β,
∵∠ABF=90°,
∴∠BAF=90°﹣β,
∵AE=CE,EF=CE,
∴AE=EF,
∴∠EAF=∠AFE,
∴α﹣(90°﹣β)=180°﹣α﹣β,
∴α+β=135°,
故选:B.
【点睛】本题考查了正方形的性质,全等三角形的判定和性质,等腰三角形的性质,三角形内角和定理,熟练掌握正方形的性质是解题的关键.
10.如图,在菱形纸片ABCD中,∠A=60°,将菱形纸片翻折,使点A落在CD的中点P处,折痕为MN,点M,N分别在边AB,AD上,则BM:AM的值为( )
A. B. C. D.
【点拨】由菱形的性质和等边三角形的性质,可得BP⊥CD,DP=a,∠DBP=30°,由勾股定理可求解.
【解析】解:如图,连接BD,BP,
设AB=2a,
∵四边形ABCD是菱形,∠A=60°,
∴AB=BC=2a=CD,∠A=∠C=60°,
∴△BCD是等边三角形,△ABD是等边三角形,
∵点P在CD的中点,
∴BP⊥CD,DP=a,∠DBP=30°,
∴BP=a,∠ABP=∠ABD+∠DBP=90°,
∵将菱形纸片翻折,
∴AM=MP,
∵MP2=MB2+BP2,
∴(2a﹣BM)2=MB2+3a2,
∴BM=a,
∴AM=a,
∴BM:AM=,
故选:B.
【点睛】本题考查了翻折变换,等边三角形的性质,菱形的性质,勾股定理,添加恰当的辅助线构造直角三角形是本题的关键.
二、填空题:本题共6小题,每小题3分,共18分。
11.如图,在矩形ABCD中,对角线AC,BD相交于点O,若OA=2,则BD的长为 4 .
【点拨】因为矩形的对角线相等且互相平分,已知OA=2,则AC=2OA=4,又BD=AC,故可求.
【解析】解:∵ABCD是矩形
∴OC=OA,BD=AC
又∵OA=2,
∴AC=OA+OC=2OA=4
∴BD=AC=4
故答案为:4.
【点睛】本题考查矩形的对角线相等的性质,属于矩形的基本性质,比较简单.
12.如图,菱形的边长是10,对角线BD的长是16,点H是边AD的中点,则OH的长是 5 .
【点拨】根据菱形的性质可得OB=OD,AO⊥BO,从而可判断OH是△ABD的中位线.
【解析】解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AO=OC,OB=OD,AO⊥BO,
∵AB=10,
又∵点H是AD中点,
∴OH是△DAB的中位线,
∴OH=AB=5.
故答案为:5.
【点睛】本题考查了菱形的性质及三角形的中位线定理,熟练掌握菱形四边相等、对角线互相垂直且平分的性质是解题关键.
13.如图,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点E,垂足为点F,连接DE,则∠CDE的度数为 75° .
【点拨】连接BE,根据菱形的对角线平分一组对角线可得∠BAC=35°,根据线段垂直平分线上的点到两端点的距离相等可得AE=BE,根据等边对等角可得∠ABE=∠BAC,再根据菱形的邻角互补求出∠ABC,然后求出∠CBE,最后根据菱形的对称性可得∠CDE=∠CBE.
【解析】解:如图,连接BE,
在菱形ABCD中,∠BAC=∠BAD=×70°=35°,
∵EF是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠BAC=35°,
∵菱形ABCD的对边AD∥BC,
∴∠ABC=180°﹣∠BAD=180°﹣70°=110°,
∴∠CBE=∠ABC﹣∠ABE=110°﹣35°=75°,
由菱形的对称性,∠CDE=∠CBE=75°.
故答案为:75°.
【点睛】本题考查了菱形的性质,线段垂直平分线上的点到两端点的距离相等的性质,等边对等角的性质,熟记各性质是解题的关键.
14.如图,长方形ABCD中,点E在边AB上,将长方形ABCD 沿图中标示的DE折叠,点A恰好落在边BC的点G处,若∠CDG=54°,则∠DEG的度数为 72 °.
【点拨】由矩形的性质得∠A=∠ADC=∠C=90°,AD∥BC,则∠ADG=∠CGD=90°﹣∠CDG=36°,由折叠得∠DGE=∠A=90°,∠GDE=∠ADE=∠ADG=18°,则∠DEG=90°﹣∠GDE=72°,于是得到问题的答案.
【解析】解:∵四边形ABCD是矩形,
∴∠A=∠ADC=∠C=90°,AD∥BC,
∵∠CDG=54°,
∴∠CGD=90°﹣∠CDG=90°﹣54°=36°,
∴∠ADG=∠CGD=36°,
∵将长方形ABCD 沿DE折叠,点A落在边BC的点G处,
∴∠DGE=∠A=90°,∠GDE=∠ADE=∠ADG=×36°=18°,
∴∠DEG=90°﹣∠GDE=90°﹣18°=72°,
故答案为:72.
【点睛】此题重点考查矩形的性质、轴对称的性质、平行线的性质、直角三角形的两个锐角互余等知识,求得∠ADG=∠CGD=36°是解题的关键.
15.正方形ABCD的边长为4.E为AD的中点,连接CE,过点B作BF⊥CE交CD于点F,垂足为G,则EG= .
【点拨】利用勾股定理可求BF的长,由面积法可求EG.
【解析】解:∵四边形ABCD是正方形,
∴AD=CD=BC,∠BCD=∠ADC=90°,
∴∠DCE+∠DEC=90°,
∵BF⊥CE,
∴∠DCE+∠CFB=90°,
∴∠BFC=∠DEC,
∴△BFC≌△CED(AAS),
∴DE=CF=2,CE=BF,
∴BF=,
∴CE=2,
∵S△BFC=×BC×CF=×BF×CG,
∴4×2=2CG,
∴CG=,
∴EG=,
故答案为:.
【点睛】考查了正方形的性质,全等三角形的判定和性质,勾股定理等知识,添加恰当辅助线构造全等三角形是解题的关键.
16.正方形ABCD的边长为3,点P、Q在正方形不同的边上与点A构成等腰三角形,若等腰△APQ的底边长为,则等腰△APQ的腰长是 2或或 .
【点拨】分三种情况进行讨论,当P、Q分别在AD、AB上,AP=AQ,当P、Q分别在CD、BD上,AP=AQ,当AP=PQ,点P在CD上,点Q在AB上,分别画出图形,根据正方形的性质和勾股定理进行求解即可.
【解析】解:当P、Q分别在AD、AB上,AP=AQ,△APQ为等腰直角三角形,如图所示:
∵,
∴;
当P、Q分别在CD、BD上,AP=AQ,如图所示:
∵四边形ABCD为正方形,
∴AB=AC=BD=CD=3,∠B=∠C=90°,
∴Rt△ABQ≌Rt△ACP,
∴BQ=CP,
∴BD﹣BQ=CD﹣CP,即DP=DQ,
∴△DPQ为等腰直角三角形,
∵,
∴,
∴BQ=3﹣2=1,
∴此时腰长为;
当AP=PQ,点P在CD上,点Q在AB上,过点P作PM⊥AB于点M,如图所示:
∵AP=PQ,PM⊥AB,,
∴,
∵∠AMP=∠CAM=∠C=90°,
∴四边形AMPC为矩形,
∴MP=AC=3,
∴.
综上分析可知:等腰△APQ的腰长是2或或.
故答案为:2或或.
【点睛】本题主要考查了等腰三角形的判定和性质,正方形的性质,勾股定理,矩形的判定和性质,解题的关键是数形结合,熟练掌握相关的判定和性质.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,矩形ABCD的对角线AC,BD相交于点O,过点D作AC的平行线交BC的延长线于点E.
(1)求证:BD=DE;
(2)连接OE,若AB=2,BC=4,求OE的长.
【点拨】(1)根据矩形的对角线相等可得AC=BD,对边平行可得AB∥CD,再求出四边形ABEC是平行四边形,根据平行四边形的对边相等可得AC=BE,从而得证;
(2)如图,过点O作OF⊥CD于点F,欲求OE,只需在直角△OEF中求得OF、FE的值即可.OF结合三角形中位线求得EF,结合矩形、平行四边形的性质以及勾股定理求得即可.
【解析】(1)证明:在矩形ABCD中,AD∥BC,AD=BC,
∴AD∥CE.
∵Ac∥DE.
∴四边形ACED是平行四边形.
∴AC=DE.
在矩形ABCD中,AC=BD,
∴BD=DE
(2)解:作OH⊥BE于H,如图.
在矩形ABCD中,AC=BD,且AC与BD交于点O,
∴OB=OC=OA.
∴BH=HC. ,
∵AB=2,BC=4,
∴OH=1,HC=2.
在平行四边形ACED中,AD=CE.
∴CE=BC=4.
∴HE=6.
在Rt△OHE中,OE=.
【点睛】本题考查了矩形的性质,平行四边形的判定与性质,熟记各性质并求出四边形ABEC是平行四边形是解题的关键.
18.已知:如图,在菱形ABCD中,过顶点D作DE⊥AB,DF⊥BC,垂足分别为E,F,连结EF.
(1)求证:△DEF为等腰三角形.
(2)若∠DEF=66°,求∠A的度数.
【点拨】(1)利用菱形的性质得到AD=CD,∠A=∠C,进而利用AAS证明两三角形全等,进而利用全等三角形的性质和等腰三角形的判定解答即可;
(2)求出∠DEF=∠DFE=66°,由菱形的性质可得出答案.
【解析】(1)证明:∵四边形ABCD是菱形,
∴AD=CD,∠A=∠C,
∵DE⊥BA,DF⊥CB,
∴∠AED=∠CFD=90°,
在△ADE和△CDF,
,
∴△ADE≌△CDF(AAS),
∴DE=DF,
∴△DEF是等腰三角形;
(2)解:∵DE=DF,
∴∠DEF=∠DFE=66°,
∴∠BEF=∠BFE=90°﹣66°=24°,
∴∠B=180°﹣24°﹣24°=132°,
∵四边形ABCD是菱形,
∴AD∥BC,
∴∠A=180°﹣∠B=48°.
【点睛】本题主要考查了菱形的性质以及全等三角形的判定与性质,解题的关键是掌握菱形的性质以及AAS证明两三角形全等,此题难度一般.
19.周末,小美和妈妈买回来一盏简单而精致的吊灯,其截面如图所示,四边形ABCD是一个菱形内框架,四边形AECF是其外部框架,且点E、B、D、F在同一直线上,BE=DF.
(1)求证:四边形外框AECF是菱形;
(2)若外框AECF的周长为80cm,EF=32cm,BE=7cm,求AB的长.
【点拨】(1)根据菱形的性质和全等三角形的判定和性质得出AE=AF=CE=CF,进而利用菱形的判定解答即可;
(2)根据菱形的性质和勾股定理得出AC,进而解答即可.
【解析】(1)证明:∵四边形ABCD是菱形,
∴AB=AD=BC=CD,∠ABD=∠CBD=∠ADB=∠CDB,
∴∠ABE=∠ADF,
在△ABE与△ADF中,
,
∴△ABE≌△ADF(SAS),
∴AE=AF,
同理可得:AE=CE=CF=AF,
∴四边形AECF是菱形;
(2)解:连接AC,交EF于点O,
∵四边形AECF是菱形,外框AECF的周长为80cm,
∴AE=20cm,EF⊥AC,OE=OF,
∵EF=32cm,BE=7cm,
∴OE=16cm,OB=16﹣7=9(cm),
∴OA=(cm),
∴AB=(cm).
【点睛】此题考查菱形的判定和性质,关键是根据四条边相等的四边形是菱形解答.
20.如图,在平行四边形ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG=AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AC=2AB时,四边形EGCF是矩形.
【点拨】(1)由平行四边形的性质得出AB=CD,AB∥CD,OB=OD,OA=OC,由平行线的性质得出∠ABE=∠CDF,证出BE=DF,由SAS证明△ABE≌△CDF即可;
(2)证出AB=OA,由等腰三角形的性质得出AG⊥OB,∠OEG=90°,同理:CF⊥OD,得出EG∥CF,由三角形中位线定理得出OE∥CG,EF∥CG,得出四边形EGCF是平行四边形,即可得出结论.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,OA=OC,
∴∠ABE=∠CDF,
∵点E,F分别为OB,OD的中点,
∴BE=OB,DF=OD,
∴BE=DF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS);
(2)证明:∵AC=2OA,AC=2AB,
∴AB=OA,
∵E是OB的中点,
∴AG⊥OB,
∴∠OEG=90°,
同理:CF⊥OD,
∴AG∥CF,
∴EG∥CF,
∵EG=AE,OA=OC,
∴OE是△ACG的中位线,
∴OE∥CG,
∴EF∥CG,
∴四边形EGCF是平行四边形,
∵∠OEG=90°,
∴四边形EGCF是矩形.
【点睛】本题考查了矩形的判定、平行四边形的性质和判定、全等三角形的判定、三角形中位线定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
21.如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连接AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
【点拨】(1)结论:AG2=GE2+GF2.只要证明GA=GC,四边形EGFC是矩形,推出GE=CF,在Rt△GFC中,利用勾股定理即可证明;
(2)过点A作AH⊥BG,在Rt△ABH、Rt△AHG中,求出AH、HG即可解决问题.
【解析】解:(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2.
(2)过点A作AH⊥BG,
∵四边形ABCD是正方形,
∴∠ABD=∠GBF=45°,
∵GF⊥BC,
∴∠BGF=45°,
∵∠AGF=105°,
∴∠AGB=∠AGF﹣∠BGF=105°﹣45°=60°,
在Rt△ABH中,∵AB=1,
∴AH=BH=,
在Rt△AGH中,∵AH=,∠GAH=30°,
∴HG=AH tan30°=,
∴BG=BH+HG=+.
解法二:如图,过点B作BN⊥AG于N,在BN上截取BM,使得BM=AM,设AN=x.
∵∠AGF=105°,∠GBF=∠FGB=∠ABG=45°,
∴∠AGB=60°,∠GBN=30°,∠ABM=∠BAM=15°,
∴∠AMN=∠ABM+∠BAM=30°,
∴AM=BM=2x,MN=x,
在Rt△ABN中,则有1=x2+(2x+x)2,
解得x=,
∴BN=,
∴BG==.
【点睛】本题考查正方形的性质、矩形的判定和性质、勾股定理直角三角形30度的性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
22.如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,且EG平分∠HEF.
(1)求证:△AEH≌△CGF.
(2)若∠EFG=90°.求证:四边形EFGH是正方形.
【点拨】(1)根据全等三角形的判定定理SAS证得结论;
(2)先证明四边形EFGH是平行四边形,再证明有一组邻边相等,然后结合∠EFG=90°,即可证得该平行四边形是正方形.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴∠A=∠C.
在△AEH与△CGF中,
,
∴△AEH≌△CGF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠B=∠D.
∵AE=CG,AH=CF,
∴EB=DG,HD=BF.
∴△BEF≌△DGH(SAS),
∴EF=HG.
又∵△AEH≌△CGF,
∴EH=GF.
∴四边形HEFG为平行四边形.
∴EH∥FG,
∴∠HEG=∠FGE.
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠FGE=∠FEG,
∴EF=GF,
∴平行四边形EFGH是菱形,
又∵∠EFG=90°,
∴菱形EFGH是正方形.
∴四边形EFGH是正方形.
【点睛】本题考查了正方形的判定,判定一个四边形是正方形的方法有:
①先判定四边形是矩形,再判定这个矩形有一组邻边相等;
②先判定四边形是菱形,再判定这个菱形有一个角为直角.
③还可以先判定四边形是平行四边形,再用1或2进行判定.
也考查了平行四边形的性质,全等三角形的判定与性质,难度适中.
23.如图,在菱形ABCD中,60°<∠ABC<90°,点E在边BC上(不与点B,点C重合),线段EC的中垂线交对角线BD于点F,连接AE,AF,EF,CF.
(1)求证:AF=EF.
(2)设∠ABC=α,∠AEF=β.圆圆同学通过画图和测量得到以下近似数据:
α 70 76 80 88
β 35 38 40 44
猜想:β关于α的函数表达式,并给出证明.
(3)若AB=AE,AB∥FE,求证:BF=CF+CE.
【点拨】(1)根据菱形的性质证明△ABF≌△CBF(SAS),根据题意线段EC的中垂线交BD于点F,即可得证.
(2)利用全等三角形的性质得出∠BAF=∠BCF,根据平角的定义,即可得证.
(3)求出β的度数,进而证得BF=BC,BE=EF,即可得证.
【解析】(1)证明:∵菱形ABCD,
∵∠ABD=∠CBD,AB=CB,
∵BF=BF,
∴△ABF≌△CBF(SAS),
∴AF=CF,
又∵线段EC的中垂线交BD于点F,
∴EF=CF,
∴AF=FE.
(2)猜想:α=2β.
证明:因为△ABF≌△CBF,
∴∠BAF=∠BCF,
∵EF=CF,
∴∠FEC=∠ECF,
∵∠FEC+∠FEB=180°,
∴∠BAF+∠FEB=180°,
∴∠ABC+∠AFE=180°,
即∠AFE=180°﹣a,
∵AF=FE,
∴,
∴α=2β.
(3)∵AB=AE,
∴∠ABE=∠AEB=2β,
∵AB∥FE,
∴∠FEC=∠ABE=2β,
∴∠FEC=∠ABE=∠AEB=∠ECF=2β,
∵∠AEB+∠ECF+∠AEF=180°,
∴β=36°,
∴∠BFC=72°,∠BFE=36°,
∵∠BFC=∠BCF=72°,
∴BF=BC,
∵∠BFE=∠FBC=36°,
∴BE=EF,
∴BF=BC=BE+CE=CF+CE.
【点睛】本题考查了四边形的综合应用,解题的关键是掌握菱形的性质,全等三角形的性质与判定.
24.在正方形ABCD中,点E在AD边上(不与点A,点D重合).连接BE,作AG⊥BE于点F,交CD边于点G,连接CF.
(1)求证:BE=AG.
(2)若点E是AD边的中点,AD=10.
①分别求AF,BF的长.
②求证:CB=CF.
【点拨】(1)根据正方形的性质及垂线的性质得出∠ABE=∠DAG,然后利用ASA得出△ABE≌△DAG,即可得解;
(2)①利用勾股定理得出BE的长,再利用面积法求解,求解即可;
②过点C作CH⊥BF于点H,先得出∠ABF=∠BCH,∠BFA=∠CHB,再得出△ABF≌△BCH,最后利用FH=BF﹣BH求解即可.
【解析】(1)证明:∵四边形ABCD是正方形,
∴∠BAE=∠ADG=90°,AB=DA,
∴∠ABE+∠AEB=90°,
∵AG⊥BE,
∴∠AFE=90°,
∴∠DAG+∠AEB=90°,
∴∠ABE=∠DAG,
在△ABE和△DAG中,
,
∴△ABE≌△DAG(ASA),
∴BE=AG;
(2)①解:∵正方形ABCD是正方形,AD=10,
∴AB=BC=AD=10,
∴AE=AD==5,
在Rt△ABE中,由勾股定理可得:
BE=,
∵ BE AF= AB AE.
∴AF=2,BF==4,
∴AF的长为2,BF的长为4.
②如图,过点C作CH⊥BF于点H,则∠CHB=90°,
∵∠CHB=90°,
∴∠CBH+∠BCH=90°,
∵∠ABC=∠ABF+∠CBH=90°,
∴∠ABF=∠BCH,
∵∠BFA=90°,
∴∠BFA=∠CHB,
在△ABF和△BCH中,
,
∴△ABF≌△BCH(AAS),
∴AF=BH=2,
∵BF=4,
∴FH=BF﹣BH=4﹣2=2,
∴BH=FH=2,
∵CH⊥BF,
∴CH是线段BF的垂直平分线,
∴CB=CF.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,勾股定理的运用,正确作出辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
