浙教版九上第一章二次函数单元竞赛测试卷
文档属性
| 名称 | 浙教版九上第一章二次函数单元竞赛测试卷 |  | |
| 格式 | docx | ||
| 文件大小 | 615.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-21 19:43:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
二次函数单元竞赛测试卷
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 5分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、选择题
得分
1.已知,若关于x的方程的解为.关于x的方程的解为.则下列结论正确的是( )
A. B.
C. D.
2.已知ac≠0,若二次函数y1=ax2+bx+c的图象与x轴交于两个不同的点A(x1,0),B(x2,0),二次函数y2=cx2+bx+a的图象与x轴交于两个不同的点C(x3,0),D(x4,0),则( )
A.x1+x2+x3+x4=1 B.x1x2x3x4=1
C. D.
3.如图,抛物线经过点,.下列结论:①;②;③若抛物线上有点,,,则;④方程的解为,,其中正确的个数是( )
A.4 B.3 C.2 D.1
4.已知二次函数y=a(x+m﹣1)(x﹣m)(a≠0)的图象上有两点A(x1,y1)和B(x2,y2)(其中x1<x2),则( )
A.若a>0,当x1+x2<1时,a(y1﹣y2)<0
B.若a>0,当x1+x2<1时,a(y1﹣y2)>0
C.若a<0,当x1+x2>﹣1时,a(y1﹣y2)<0
D.若a<0,当x1+x2>﹣1时,a(y1﹣y2)>0
5.已知抛物线过点,且,则关于的一元二次方程的解为( )
A. B.
C. D.
6. 二次函数(m是常数).不论m为何值,该函数的图象与x轴( )
A.两个不同的交点 B.两个相同的交点
C.没有交点 D.无法判断
7.如图,已知抛物线与直线交于两点,则关于的不等式的解集是( )
A.或 B.或
C. D.
8.题目:“已知二次函数的图象与轴交于点,过点作直线平行于轴,将抛物线位于直线下方的部分翻折至直线上方,将这部分图象与拋物线剩余部分组成的新图象记为.若图象与轴有4个交点,求的取值范围.”对于其答案,甲答:,乙答:,丙答:,则正确的是( )
A.只有甲答的对 B.只有乙答的对
C.甲、丙答案合在一起才完整 D.乙、丙答案合在一起才完整
9.如图,二次函数及一次函数,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数,当直线与新图象有4个交点时,m的取值范围是( )
A. B. C. D.
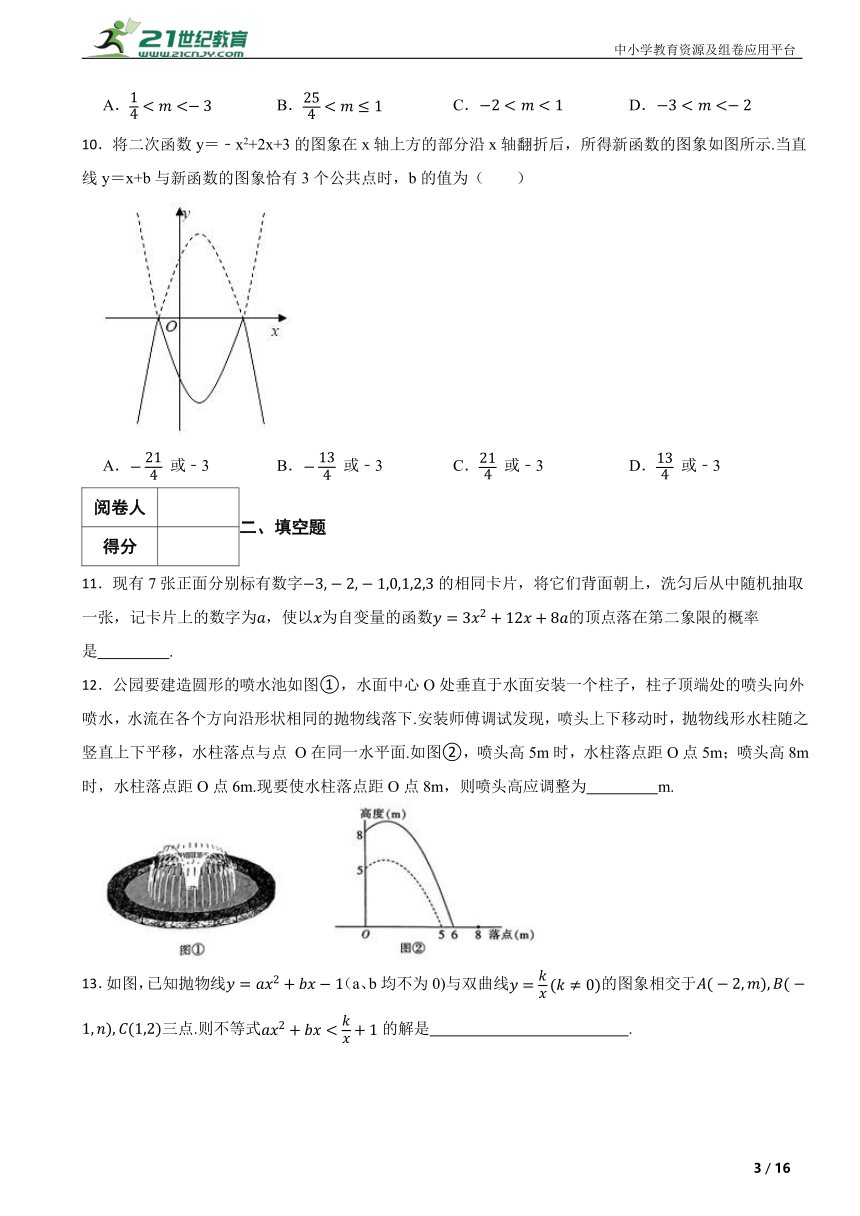
10.将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )
A. 或﹣3 B. 或﹣3 C. 或﹣3 D. 或﹣3
阅卷人 二、填空题
得分
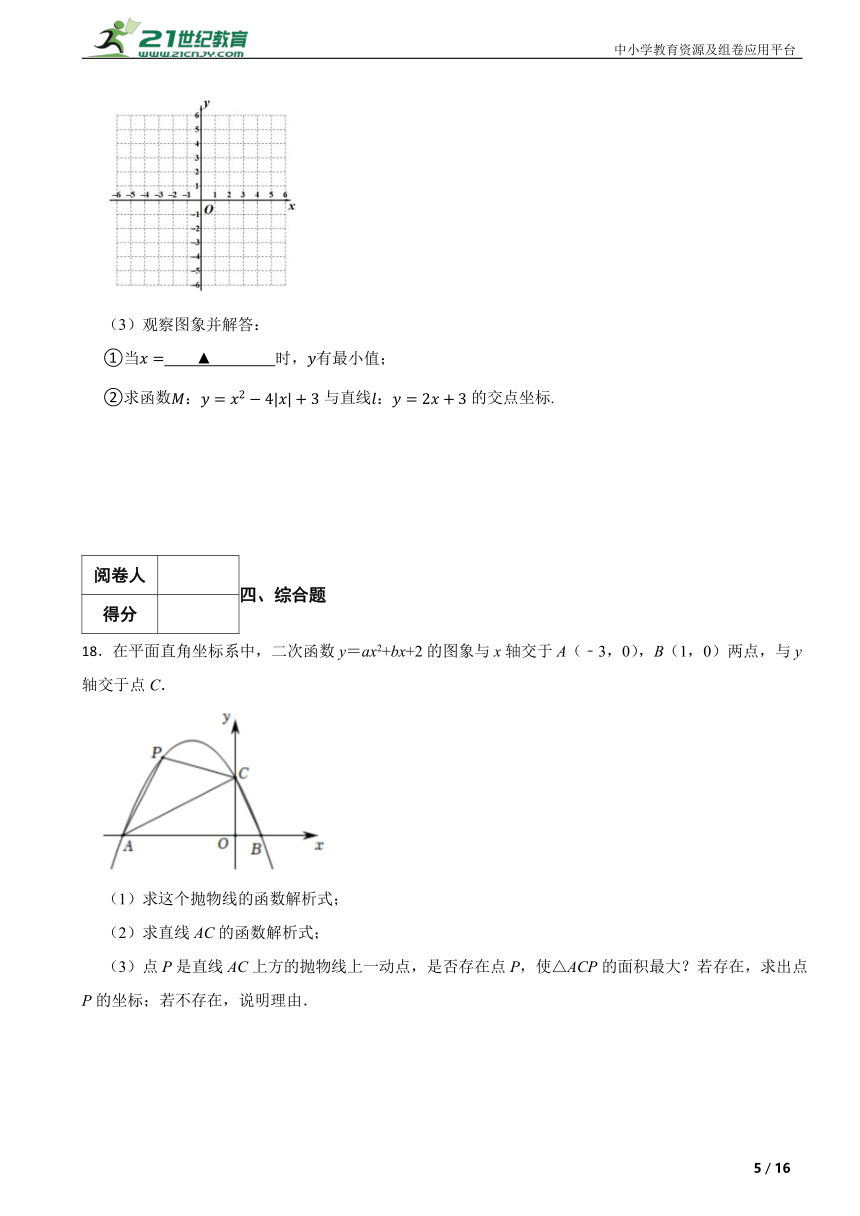
11.现有7张正面分别标有数字的相同卡片,将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为,使以为自变量的函数的顶点落在第二象限的概率是 .
12.公园要建造圆形的喷水池如图①,水面中心O处垂直于水面安装一个柱子,柱子顶端处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下.安装师傅调试发现,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点 O在同一水平面.如图②,喷头高5m时,水柱落点距O点5m;喷头高8m时,水柱落点距O点6m.现要使水柱落点距O点8m,则喷头高应调整为 m.
13.如图,已知抛物线(a、b均不为0)与双曲线的图象相交于三点.则不等式的解是 .
14.在平面直角坐标系中,为坐标原点,抛物线与轴交于点,过点作轴的平行线交抛物线于点,抛物线顶点为.若直线交直线于点,且,则的值为 .
15. 关于的二次函数,在时有最大值6,则 .
16.如图,抛物线与x轴交于A、B两点,与y轴交于C点,P为抛物线对称轴上动点,则取最小值时,点P坐标是 .
第Ⅱ卷 主观题
第Ⅱ卷的注释
阅卷人 三、作图题
得分
17.小明探究函数的图象和性质的过程如下,请按要求回答问题:
(1)列表:
-4 -3 -2 -1 0 1 2 3 4
0 -1 0 3 0 0 3
表格中, , .
(2)在如图所示的坐标系中进行描点,并画出函数的图象.
(3)观察图象并解答:
①当 ▲ 时,有最小值;
②求函数与直线的交点坐标.
阅卷人 四、综合题
得分
18.在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
(1)求这个抛物线的函数解析式;
(2)求直线AC的函数解析式;
(3)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由.
19.如图,在平面直角坐标系中,抛物线与x轴交于点,两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)点P是直线下方抛物线上一动点,过点P作轴交于点E,求的最大值及此时点P的坐标;
(3)将该抛物线沿x轴向右平移4个单位长度得到新抛物线,点N是原抛物线上一点,在新抛物线的对称轴上是否存在一点M,使得以B,C,N,M为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标,并选择一个你喜欢的点写出求解过程;若不存在,请说明理由.
20.根据以下素材,探索完成任务.
如何设计跳长绳方案
素材1 图1是集体跳长绳比赛,比赛时,各队跳绳10人,摇绳2人,共计12人.图2是绳甩到最高处时的示意图,可以近似的看作一条抛物线,正在甩绳的甲、乙两位队员拿绳的手间距6米,到地面的距离均为1米,绳子最高点距离地面2.5米.
素材2 某队跳绳成员有6名男生和4名女生,男生身高1.70米至1.80米,女生身高1.66米至1.68米.跳长绳比赛时,可以采用一路纵队或两路纵队并排的方式安排队员位置,但为了保证安全,人与人之间距离至少0.5米.
问题解决
任务1 确定长绳形状 在图2中建立合适的直角坐标系,并求出抛物线的函数表达式.
任务2 探究站队方式 当该队以一路纵队的方式跳绳时,绳子能否顺利的甩过所有队员的头顶?
任务3 拟定位置方案 为了更顺利的完成跳绳,现按中间高两边低的方式居中安排站位.请在你所建立的坐标系中,求出左边第一位跳绳队员横坐标的最大取值范围.
21.如图,在平面直角坐标系中,抛物线过点,且交轴于点,两点,交轴于点.
(1)求抛物线的表达式;
(2)点是直线上方抛物线上的一动点,过点作于点,过点作轴的平行线交直线于点.
①当点P运动到抛物线顶点时,求此时的面积.
②点在运动的过程中,是否存在周长的最大值,若存在,请求出周长的最大值及此时点的坐标;若不存在,请说明理由.
22.为了振兴乡村经济,增加村民收入,某村委会干部带领村民把一片坡地改造后种植了优质葡萄,今年正式上市销售,并在网上直播推销优质葡萄.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第天的售价为y元/千克,y关于x的函数解析式为且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售葡萄的成本是18元/千克,每天的利润是元.
(1) , ;
(2)销售优质葡萄第几天时,当天的利润最大?最大利润是多少?
23.如图,在平面直角坐标系中,抛物线 与x轴交于点,点,与y轴交于点.
(1)求抛物线的函数表达式;
(2)在对称轴上找一点Q,使的周长最小,求点Q的坐标;
(3)在(2)的条件下,点P是抛物线上的一点,当和面积相等时,请求出所有点P的坐标.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】D
10.【答案】A
11.【答案】
12.【答案】16
13.【答案】-2<x<-1或0<x<1
14.【答案】或
15.【答案】2或
16.【答案】
17.【答案】(1)3;-1
(2)解:如图所示:
(3)解:①;
②,
当时,联立方程组,解得或,
与的交点坐标为和;
当时,,解得或(舍去).
综上,与直线的交点坐标为,,
18.【答案】(1)解:将点A(﹣3,0),B(1,0)代入y=ax2+bx+2中,
∴,
解得.
∴y=﹣+2
(2)解:令x=0,则y=2,
∴C(0,2),
设直线AC的解析式为y=kx+c,
∴,
解得,
∴直线AC的函数解析式为y=x+2
(3)解:存在点P,使△ACP的面积最大,
如图,过点P作PG∥y轴交AC于点G,
设P(t,),则G(t,+2),
∴PG=,
∴S△ACP=
∵点P是直线AC上方,
∴﹣3<t<0,
∴当时,S有最大值,
此时P
19.【答案】(1)解:将,代入,
∴,
解得:,
∴抛物线的函数表达式为;
(2)解:当时,,
∴,
设直线的解析式为,
∴,
解得:,
∴,
设,则,
∴,
当时,有最大值,此时;
(3)解:存在点M,使得以B,C,N,M为顶点的四边形是平行四边形,理由如下:
由题意可得,平移后的抛物线解析式为,
∴抛物线的对称轴为直线,
设,,
当为平行四边形的对称轴时,,,
解得,,
∴;
当为平行四边形的对角线时,,,
解得,,
∴;
当为平行四边形的对角线时,,,
解得,,
∴;
综上所述:M点坐标为或或.
20.【答案】解:任务一:
以左边摇绳人与地面的交点为原点,地面所在直线为 轴,建立直角坐标系,如图:
由已知可得, , 在抛物线上,且抛物线顶点的纵坐标为 ,
设抛物线解析式为 ,
∴ ,
解得 ,
∴抛物线的函数解析式为 ;
任务二:
∵ ,
∴抛物线的对称轴为直线 ,
名同学,以直线 为对称轴,分布在对称轴两侧,男同学站中间,女同学站两边,对称轴左侧的 位男同学所在位置横坐标分布是 , 和 ,
当 时, ,
∴绳子能顺利的甩过男队员的头顶,
同理当 时, ,
∴绳子不能顺利的甩过女队员的头顶;
∴绳子不能顺利的甩过所有队员的头顶;
任务三:
两路并排,一排 人,
当 时, ,
解得 或 ,
但第一位跳绳队员横坐标需不大于 (否则第二、三位队员的间距不够 米)
∴ .
21.【答案】(1)解:由题意得:,
解得:,
则抛物线的表达式为:;
(2)解:①令,
解得或3,即点,
令,则,即点,
直线的表达式为:,
,
,
,
点是抛物线的顶点,
点,
轴,
点的横坐标为
点,
,
,
,,
,
,
,
的面积为1.
②存在,设点,则点,
则,
,抛物线开口向下,
当时,最大,为:,
,
∴,
当最大时,即时,最大
,
,
周长的最大值为,
此时点的坐标为:.
22.【答案】(1);25
(2)解:由(1)知第天的销售量为千克.
当时,
,
当时,取得最大值,最大值为968.
当时,.
,随的增大而增大,
.
,当时,.
答:销售优质葡萄第18天时,当天的利润最大,最大利润是968元.
23.【答案】(1)解:∵抛物线与x轴交于点,点,与y轴交于点,
∴,
∴,
∴抛物线解析式为;
(2)解:如图,连接交对称轴于点Q,
∵抛物线解析式为,
∴抛物线的对称轴为直线,
∵点A,B关于对称轴对称,
∴,
∴,
∴当C,B,Q三点共线时,的周长最小,
∵,,
设直线的解析式为,
∴,
∴
∴直线的解析式为,
在中,当时,,
∴;
(3)解:同理可求出直线的解析式,
过点C作的平行线,交抛物线于点,
同理可求出直线的解析式为,
联立,解得或(舍去),
∴;
∵直线与y轴的交点为,点到的距离为2个单位,根据平行线间间距相等可知将直线向上平移2个单位,得到直线,其与抛物线的两个交点也符合题意,
联立,解得或
同理可得,,
综上所述:点P的坐标为,,.
1 / 1
二次函数单元竞赛测试卷
注意事项:
1、填写答题卡的内容用2B铅笔填写
2、提前 5分钟收取答题卡
第Ⅰ卷 客观题
第Ⅰ卷的注释
阅卷人 一、选择题
得分
1.已知,若关于x的方程的解为.关于x的方程的解为.则下列结论正确的是( )
A. B.
C. D.
2.已知ac≠0,若二次函数y1=ax2+bx+c的图象与x轴交于两个不同的点A(x1,0),B(x2,0),二次函数y2=cx2+bx+a的图象与x轴交于两个不同的点C(x3,0),D(x4,0),则( )
A.x1+x2+x3+x4=1 B.x1x2x3x4=1
C. D.
3.如图,抛物线经过点,.下列结论:①;②;③若抛物线上有点,,,则;④方程的解为,,其中正确的个数是( )
A.4 B.3 C.2 D.1
4.已知二次函数y=a(x+m﹣1)(x﹣m)(a≠0)的图象上有两点A(x1,y1)和B(x2,y2)(其中x1<x2),则( )
A.若a>0,当x1+x2<1时,a(y1﹣y2)<0
B.若a>0,当x1+x2<1时,a(y1﹣y2)>0
C.若a<0,当x1+x2>﹣1时,a(y1﹣y2)<0
D.若a<0,当x1+x2>﹣1时,a(y1﹣y2)>0
5.已知抛物线过点,且,则关于的一元二次方程的解为( )
A. B.
C. D.
6. 二次函数(m是常数).不论m为何值,该函数的图象与x轴( )
A.两个不同的交点 B.两个相同的交点
C.没有交点 D.无法判断
7.如图,已知抛物线与直线交于两点,则关于的不等式的解集是( )
A.或 B.或
C. D.
8.题目:“已知二次函数的图象与轴交于点,过点作直线平行于轴,将抛物线位于直线下方的部分翻折至直线上方,将这部分图象与拋物线剩余部分组成的新图象记为.若图象与轴有4个交点,求的取值范围.”对于其答案,甲答:,乙答:,丙答:,则正确的是( )
A.只有甲答的对 B.只有乙答的对
C.甲、丙答案合在一起才完整 D.乙、丙答案合在一起才完整
9.如图,二次函数及一次函数,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新函数,当直线与新图象有4个交点时,m的取值范围是( )
A. B. C. D.
10.将二次函数y=﹣x2+2x+3的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线y=x+b与新函数的图象恰有3个公共点时,b的值为( )
A. 或﹣3 B. 或﹣3 C. 或﹣3 D. 或﹣3
阅卷人 二、填空题
得分
11.现有7张正面分别标有数字的相同卡片,将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为,使以为自变量的函数的顶点落在第二象限的概率是 .
12.公园要建造圆形的喷水池如图①,水面中心O处垂直于水面安装一个柱子,柱子顶端处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下.安装师傅调试发现,喷头上下移动时,抛物线形水柱随之竖直上下平移,水柱落点与点 O在同一水平面.如图②,喷头高5m时,水柱落点距O点5m;喷头高8m时,水柱落点距O点6m.现要使水柱落点距O点8m,则喷头高应调整为 m.
13.如图,已知抛物线(a、b均不为0)与双曲线的图象相交于三点.则不等式的解是 .
14.在平面直角坐标系中,为坐标原点,抛物线与轴交于点,过点作轴的平行线交抛物线于点,抛物线顶点为.若直线交直线于点,且,则的值为 .
15. 关于的二次函数,在时有最大值6,则 .
16.如图,抛物线与x轴交于A、B两点,与y轴交于C点,P为抛物线对称轴上动点,则取最小值时,点P坐标是 .
第Ⅱ卷 主观题
第Ⅱ卷的注释
阅卷人 三、作图题
得分
17.小明探究函数的图象和性质的过程如下,请按要求回答问题:
(1)列表:
-4 -3 -2 -1 0 1 2 3 4
0 -1 0 3 0 0 3
表格中, , .
(2)在如图所示的坐标系中进行描点,并画出函数的图象.
(3)观察图象并解答:
①当 ▲ 时,有最小值;
②求函数与直线的交点坐标.
阅卷人 四、综合题
得分
18.在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.
(1)求这个抛物线的函数解析式;
(2)求直线AC的函数解析式;
(3)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由.
19.如图,在平面直角坐标系中,抛物线与x轴交于点,两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)点P是直线下方抛物线上一动点,过点P作轴交于点E,求的最大值及此时点P的坐标;
(3)将该抛物线沿x轴向右平移4个单位长度得到新抛物线,点N是原抛物线上一点,在新抛物线的对称轴上是否存在一点M,使得以B,C,N,M为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标,并选择一个你喜欢的点写出求解过程;若不存在,请说明理由.
20.根据以下素材,探索完成任务.
如何设计跳长绳方案
素材1 图1是集体跳长绳比赛,比赛时,各队跳绳10人,摇绳2人,共计12人.图2是绳甩到最高处时的示意图,可以近似的看作一条抛物线,正在甩绳的甲、乙两位队员拿绳的手间距6米,到地面的距离均为1米,绳子最高点距离地面2.5米.
素材2 某队跳绳成员有6名男生和4名女生,男生身高1.70米至1.80米,女生身高1.66米至1.68米.跳长绳比赛时,可以采用一路纵队或两路纵队并排的方式安排队员位置,但为了保证安全,人与人之间距离至少0.5米.
问题解决
任务1 确定长绳形状 在图2中建立合适的直角坐标系,并求出抛物线的函数表达式.
任务2 探究站队方式 当该队以一路纵队的方式跳绳时,绳子能否顺利的甩过所有队员的头顶?
任务3 拟定位置方案 为了更顺利的完成跳绳,现按中间高两边低的方式居中安排站位.请在你所建立的坐标系中,求出左边第一位跳绳队员横坐标的最大取值范围.
21.如图,在平面直角坐标系中,抛物线过点,且交轴于点,两点,交轴于点.
(1)求抛物线的表达式;
(2)点是直线上方抛物线上的一动点,过点作于点,过点作轴的平行线交直线于点.
①当点P运动到抛物线顶点时,求此时的面积.
②点在运动的过程中,是否存在周长的最大值,若存在,请求出周长的最大值及此时点的坐标;若不存在,请说明理由.
22.为了振兴乡村经济,增加村民收入,某村委会干部带领村民把一片坡地改造后种植了优质葡萄,今年正式上市销售,并在网上直播推销优质葡萄.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第天的售价为y元/千克,y关于x的函数解析式为且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售葡萄的成本是18元/千克,每天的利润是元.
(1) , ;
(2)销售优质葡萄第几天时,当天的利润最大?最大利润是多少?
23.如图,在平面直角坐标系中,抛物线 与x轴交于点,点,与y轴交于点.
(1)求抛物线的函数表达式;
(2)在对称轴上找一点Q,使的周长最小,求点Q的坐标;
(3)在(2)的条件下,点P是抛物线上的一点,当和面积相等时,请求出所有点P的坐标.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】D
10.【答案】A
11.【答案】
12.【答案】16
13.【答案】-2<x<-1或0<x<1
14.【答案】或
15.【答案】2或
16.【答案】
17.【答案】(1)3;-1
(2)解:如图所示:
(3)解:①;
②,
当时,联立方程组,解得或,
与的交点坐标为和;
当时,,解得或(舍去).
综上,与直线的交点坐标为,,
18.【答案】(1)解:将点A(﹣3,0),B(1,0)代入y=ax2+bx+2中,
∴,
解得.
∴y=﹣+2
(2)解:令x=0,则y=2,
∴C(0,2),
设直线AC的解析式为y=kx+c,
∴,
解得,
∴直线AC的函数解析式为y=x+2
(3)解:存在点P,使△ACP的面积最大,
如图,过点P作PG∥y轴交AC于点G,
设P(t,),则G(t,+2),
∴PG=,
∴S△ACP=
∵点P是直线AC上方,
∴﹣3<t<0,
∴当时,S有最大值,
此时P
19.【答案】(1)解:将,代入,
∴,
解得:,
∴抛物线的函数表达式为;
(2)解:当时,,
∴,
设直线的解析式为,
∴,
解得:,
∴,
设,则,
∴,
当时,有最大值,此时;
(3)解:存在点M,使得以B,C,N,M为顶点的四边形是平行四边形,理由如下:
由题意可得,平移后的抛物线解析式为,
∴抛物线的对称轴为直线,
设,,
当为平行四边形的对称轴时,,,
解得,,
∴;
当为平行四边形的对角线时,,,
解得,,
∴;
当为平行四边形的对角线时,,,
解得,,
∴;
综上所述:M点坐标为或或.
20.【答案】解:任务一:
以左边摇绳人与地面的交点为原点,地面所在直线为 轴,建立直角坐标系,如图:
由已知可得, , 在抛物线上,且抛物线顶点的纵坐标为 ,
设抛物线解析式为 ,
∴ ,
解得 ,
∴抛物线的函数解析式为 ;
任务二:
∵ ,
∴抛物线的对称轴为直线 ,
名同学,以直线 为对称轴,分布在对称轴两侧,男同学站中间,女同学站两边,对称轴左侧的 位男同学所在位置横坐标分布是 , 和 ,
当 时, ,
∴绳子能顺利的甩过男队员的头顶,
同理当 时, ,
∴绳子不能顺利的甩过女队员的头顶;
∴绳子不能顺利的甩过所有队员的头顶;
任务三:
两路并排,一排 人,
当 时, ,
解得 或 ,
但第一位跳绳队员横坐标需不大于 (否则第二、三位队员的间距不够 米)
∴ .
21.【答案】(1)解:由题意得:,
解得:,
则抛物线的表达式为:;
(2)解:①令,
解得或3,即点,
令,则,即点,
直线的表达式为:,
,
,
,
点是抛物线的顶点,
点,
轴,
点的横坐标为
点,
,
,
,,
,
,
,
的面积为1.
②存在,设点,则点,
则,
,抛物线开口向下,
当时,最大,为:,
,
∴,
当最大时,即时,最大
,
,
周长的最大值为,
此时点的坐标为:.
22.【答案】(1);25
(2)解:由(1)知第天的销售量为千克.
当时,
,
当时,取得最大值,最大值为968.
当时,.
,随的增大而增大,
.
,当时,.
答:销售优质葡萄第18天时,当天的利润最大,最大利润是968元.
23.【答案】(1)解:∵抛物线与x轴交于点,点,与y轴交于点,
∴,
∴,
∴抛物线解析式为;
(2)解:如图,连接交对称轴于点Q,
∵抛物线解析式为,
∴抛物线的对称轴为直线,
∵点A,B关于对称轴对称,
∴,
∴,
∴当C,B,Q三点共线时,的周长最小,
∵,,
设直线的解析式为,
∴,
∴
∴直线的解析式为,
在中,当时,,
∴;
(3)解:同理可求出直线的解析式,
过点C作的平行线,交抛物线于点,
同理可求出直线的解析式为,
联立,解得或(舍去),
∴;
∵直线与y轴的交点为,点到的距离为2个单位,根据平行线间间距相等可知将直线向上平移2个单位,得到直线,其与抛物线的两个交点也符合题意,
联立,解得或
同理可得,,
综上所述:点P的坐标为,,.
1 / 1
同课章节目录
