第二章 特殊三角形2.1-2.5测试卷(无答案)
文档属性
| 名称 | 第二章 特殊三角形2.1-2.5测试卷(无答案) |

|
|
| 格式 | rar | ||
| 文件大小 | 30.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-07 00:00:00 | ||
图片预览

文档简介
第二章 特殊三角形2.1-2.5测试卷
出卷人:郑勇 校验人:黄林克 郑建春 验审人:林少炜
班级__________姓名______________得分______________
一、选择题(10*3=30)
1、已知等腰三角形的两边长分别为4、9,则它的周长为( )
(A)17 (B)22 (C)17或22 (D)13
2、 等边三角形的对称轴有 ( )
A 1 条 B 2条 C 3条 D 4条
3、等腰三角形的一个顶角为40 ,则它的底角为( )
(A)100 (B)40 (C)70 (D)70 或40
4、下列能断定△ABC为等腰三角形的是( )
(A)∠A=30 、∠B=60 (B)∠A=50 、∠B=80
(C)AB=AC=2,BC=4 (D)AB=3、BC=7,周长为13
5、若一个三角形有两条边相等,且有一内角为60 ,那么这个三角形一定为( )
(A)等边三角形 (B)等腰三角形 (C)直角三角形 (D)钝角三角形
6、如图6所示,∠BCA=90,CD⊥AB,则图中与∠A互余的角有( )个
A.1个 B、2个 C、3个 D、4个
7.在△ABC中,∠A:∠B:∠C=1:2:3,CD⊥AB于D,AB=a,则DB等于( )
(A) (B) (C) (D)以上结果都不对
8.如图4所示,△ABC中,AB=AC,过AC上一点作DE⊥AC,EF⊥BC,若∠BDE=140°,则∠DEF=( )
(A)55° (B)60° (C)65° (D)70°
( http: / / )
(4) (5) (6)
9.如图5所示,在△ABC中,∠A:∠B:∠C=3:5:10,又△A′B′C′≌△ABC,
则∠BCA′:∠BCB′等于( )
(A)1:2 (B)1:3 (C)2:3 (D)1:4
10.等腰三角形一腰上的高与另一腰的夹角为40°,则其顶角为( )
(A)50° (B)130°
(C)50°或130° (D)55°或130°
二.填空题(3*8=24)
1、在Rt△ABC中,∠C=90度,∠B=25度,则∠A=______度
2、已知等边三角形的周长为24cm,则等边三角形的边长为_______cm
3、Rt△ABC的斜边AB的长为10cm,则AB边上的中线长为________
4、在Rt△ABC中,∠C=90 ,∠A=30 ,BC=2cm,则AB=_____cm。
5、等边三角形两条高线相交所成的钝角为________度
6、若直角三角形的两个锐角之差为24度,则较大的锐角的度数是_________ 。
7、如图,在△ABC中,AB=AC,∠BAC与∠ACB的平分线AF、CE相交于点D,且∠B=70 ,则∠ADE的度数为_________
8、已知等腰△ABC的底边BC=8cm,且│AC-BC│=2cm,那么腰AC的长为________
三、解答题(4)
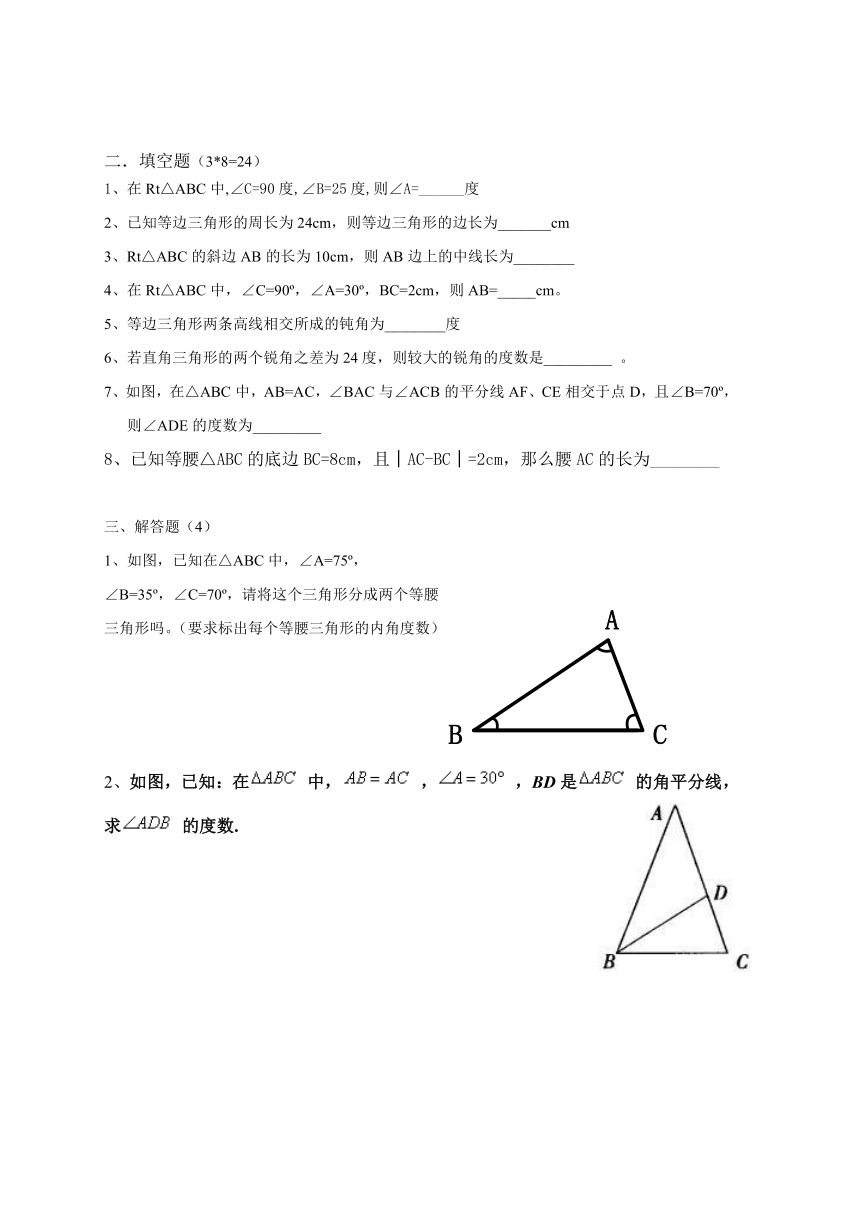
1、如图,已知在△ABC中,∠A=75 ,
∠B=35 ,∠C=70 ,请将这个三角形分成两个等腰
三角形吗。(要求标出每个等腰三角形的内角度数)
2、如图,已知:在 中, , ,BD是 的角平分线,求 的度数.
3、如图所示,已知:AB=BC=AC,CD=DE=EC,求证:AD=BE.
20.如图,已知:在等边三角形ABC中,D、E分别在AB和AC上,且AD=CE ,BE和CD相交于点P。
(1)说明△AD≌△CEB
(2)求:∠BPC 的度数.
4、如图,ADBC中,∠A=∠B=90度,E是AB上一点,且AE=BC,∠1=∠2
(1) Rt△ADE与Rt△BEC全等吗?请说明理由。
(2) △CDE是不是直角三角形?请说明理由。
5、如图,在△ABC中, P是的BC边上一点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R,若AQ=AR,则△ABC是等腰三角形吗?请说明理由。
6、想一想(附加10分,不记入总分)
在ΔABC中,AB=AC
1(1),如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=__________
(2),如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=__________
(3),思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:____________________
2 如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由
(1) (2) (3)
出卷人:郑勇 校验人:黄林克 郑建春 验审人:林少炜
班级__________姓名______________得分______________
一、选择题(10*3=30)
1、已知等腰三角形的两边长分别为4、9,则它的周长为( )
(A)17 (B)22 (C)17或22 (D)13
2、 等边三角形的对称轴有 ( )
A 1 条 B 2条 C 3条 D 4条
3、等腰三角形的一个顶角为40 ,则它的底角为( )
(A)100 (B)40 (C)70 (D)70 或40
4、下列能断定△ABC为等腰三角形的是( )
(A)∠A=30 、∠B=60 (B)∠A=50 、∠B=80
(C)AB=AC=2,BC=4 (D)AB=3、BC=7,周长为13
5、若一个三角形有两条边相等,且有一内角为60 ,那么这个三角形一定为( )
(A)等边三角形 (B)等腰三角形 (C)直角三角形 (D)钝角三角形
6、如图6所示,∠BCA=90,CD⊥AB,则图中与∠A互余的角有( )个
A.1个 B、2个 C、3个 D、4个
7.在△ABC中,∠A:∠B:∠C=1:2:3,CD⊥AB于D,AB=a,则DB等于( )
(A) (B) (C) (D)以上结果都不对
8.如图4所示,△ABC中,AB=AC,过AC上一点作DE⊥AC,EF⊥BC,若∠BDE=140°,则∠DEF=( )
(A)55° (B)60° (C)65° (D)70°
( http: / / )
(4) (5) (6)
9.如图5所示,在△ABC中,∠A:∠B:∠C=3:5:10,又△A′B′C′≌△ABC,
则∠BCA′:∠BCB′等于( )
(A)1:2 (B)1:3 (C)2:3 (D)1:4
10.等腰三角形一腰上的高与另一腰的夹角为40°,则其顶角为( )
(A)50° (B)130°
(C)50°或130° (D)55°或130°
二.填空题(3*8=24)
1、在Rt△ABC中,∠C=90度,∠B=25度,则∠A=______度
2、已知等边三角形的周长为24cm,则等边三角形的边长为_______cm
3、Rt△ABC的斜边AB的长为10cm,则AB边上的中线长为________
4、在Rt△ABC中,∠C=90 ,∠A=30 ,BC=2cm,则AB=_____cm。
5、等边三角形两条高线相交所成的钝角为________度
6、若直角三角形的两个锐角之差为24度,则较大的锐角的度数是_________ 。
7、如图,在△ABC中,AB=AC,∠BAC与∠ACB的平分线AF、CE相交于点D,且∠B=70 ,则∠ADE的度数为_________
8、已知等腰△ABC的底边BC=8cm,且│AC-BC│=2cm,那么腰AC的长为________
三、解答题(4)
1、如图,已知在△ABC中,∠A=75 ,
∠B=35 ,∠C=70 ,请将这个三角形分成两个等腰
三角形吗。(要求标出每个等腰三角形的内角度数)
2、如图,已知:在 中, , ,BD是 的角平分线,求 的度数.
3、如图所示,已知:AB=BC=AC,CD=DE=EC,求证:AD=BE.
20.如图,已知:在等边三角形ABC中,D、E分别在AB和AC上,且AD=CE ,BE和CD相交于点P。
(1)说明△AD≌△CEB
(2)求:∠BPC 的度数.
4、如图,ADBC中,∠A=∠B=90度,E是AB上一点,且AE=BC,∠1=∠2
(1) Rt△ADE与Rt△BEC全等吗?请说明理由。
(2) △CDE是不是直角三角形?请说明理由。
5、如图,在△ABC中, P是的BC边上一点,过点P作BC的垂线,交AB于点Q,交CA的延长线于点R,若AQ=AR,则△ABC是等腰三角形吗?请说明理由。
6、想一想(附加10分,不记入总分)
在ΔABC中,AB=AC
1(1),如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC=__________
(2),如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC=__________
(3),思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:____________________
2 如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由
(1) (2) (3)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
