浙教版九年级数学上册第二章第三节二次函数的性质
文档属性
| 名称 | 浙教版九年级数学上册第二章第三节二次函数的性质 |  | |
| 格式 | rar | ||
| 文件大小 | 151.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-08 09:30:00 | ||
图片预览




文档简介
课件17张PPT。二次函数的图象与性质探究如图是一个汽车隧道,形状成抛物线,隧道路面宽10米,顶部到地面的距离为10米.高4米,宽4米的一辆厢式货车能否顺利经过这条单向行车的隧道?
?10米10米若此隧道是双向车道,那么这辆货车又能否顺利经过隧道?
探究如图是一个汽车隧道,形状成抛物线,隧道路面宽10米,顶部到地面的距离为10米.高4米,宽4米的一辆厢式货车能否顺利经过这条单向行车的隧道?
?10米10米若此隧道是双向车道,那么这辆货车又能否顺利经过隧道?
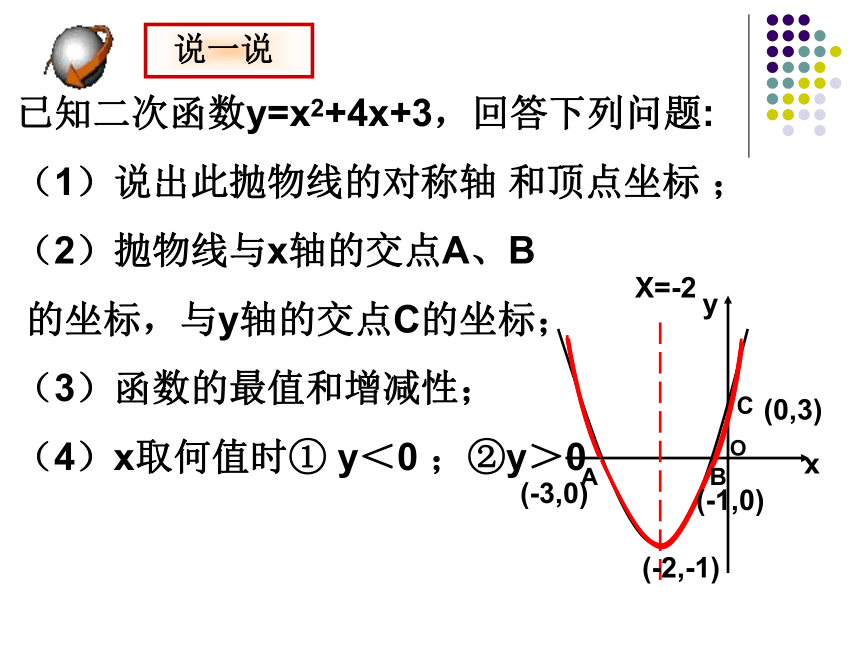
已知二次函数y=x2+4x+3,回答下列问题:
(1)说出此抛物线的对称轴 和顶点坐标 ;
(2)抛物线与x轴的交点A、B
的坐标,与y轴的交点C的坐标;
(3)函数的最值和增减性;
(4)x取何值时① y<0 ;②y>0
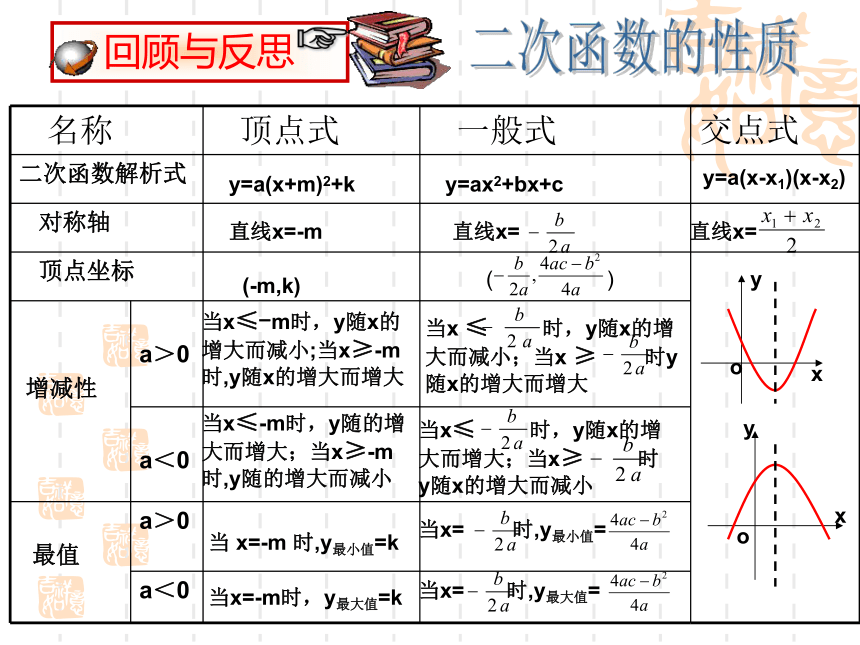
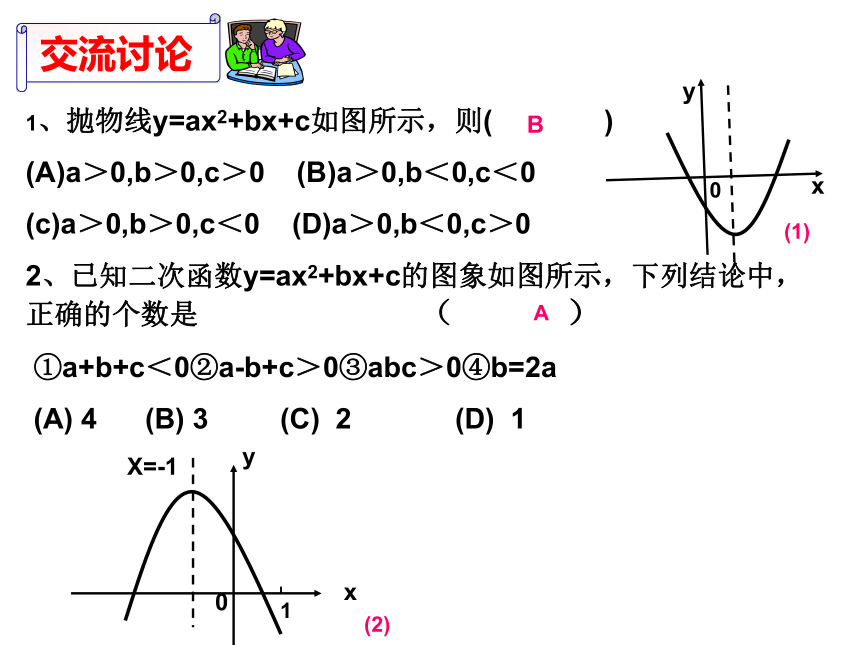
xyABOCX=-2(-3,0)(-1,0)(-2,-1)(0,3) 说一说二次函数的性质y=a(x+m)2+ky=ax2+bx+cy=a(x-x1)(x-x2)直线x=-m直线x=直线x=(-m,k)( ) 当x≤-m时,y随x的增大而减小;当x≥-m时,y随x的增大而增大当x ≤ 时,y随x的增大而减小;当x ≥ 时y随x的增大而增大当x≤-m时,y随的增大而增大;当x≥-m时,y随的增大而减小当x≤ 时,y随x的增大而增大;当x≥ 时y随x的增大而减小当 x=-m 时,y最小值=k当x= 时,y最小值=当x=-m时,y最大值=k当x= 时,y最大值=yxooyx1、若抛物线y=ax2+3x-4与抛物线y=-2x2形状相同,则a= .2、二次函数y=x2+1的图象的顶点坐标是 .3、二次函数y=ax2+bx+c的图象与x轴的两个交点分别为A(1,0),B(-3,0)则它的对称轴是 .4、二次函数y=x2-2x+2 当x= 时,y的最小值为 .5、二次函数y=4x2+mx+1的图象顶点在x轴上,则m= ;若它的顶点在y轴上,则m= .±2(0,1)直线x=-111±40X=1、抛物线y=ax2+bx+c如图所示,则( )
(A)a>0,b>0,c>0 (B)a>0,b<0,c<0
(c)a>0,b>0,c<0 (D)a>0,b<0,c>0
2、已知二次函数y=ax2+bx+c的图象如图所示,下列结论中,正确的个数是 ( )
①a+b+c<0②a-b+c>0③abc>0④b=2a
(A) 4 (B) 3 (C) 2 (D) 1xyxyX=-10(2)(1)BC1A看方向 (上正、下负)看交点 (上正、下负)二次函数的图象看对称轴(左同、右异) 开启 智慧
你说 我说1、函数y=ax2+bx+c的图象如图所示。X= 为该函数图象的对称轴,根据这个函数图象,你能得到关于该函数的哪些性质和结论?xyX=o-11-1例:已知抛物线y=x2+(2n-1)x+n2-1(n为常数)
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数解析式;
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C。
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请你求出这个最大值,并指出此时A点的坐标;如果不存在,请说出你的理由。 尝试拓展 发展思维?行家看“门道”(1)通过本节课的学习你对二次函数的图象与性质有什么的认识?
探究如图是一个汽车隧道,形状成抛物线,隧道路面宽10米,顶部到地面的距离为10米.高4米,宽4米的一辆厢式货车能否顺利经过这条单向行车的隧道?
?10米10米若此隧道是双向车道,那么这辆货车又能否顺利经过隧道?
探究如图是一个汽车隧道,形状成抛物线,隧道路面宽10米,顶部到地面的距离为10米.高4米,宽4米的一辆厢式货车能否顺利经过这条单向行车的隧道?
?10米10米若此隧道是双向车道,那么这辆货车又能否顺利经过隧道?
1、已知对于x的所有实数,函数y=x2-4kx+2k+30的值均为非负数,化简:2、已知抛物线y=(m-1)x2+4x-3开口向上,与x轴相交于A(x1,0)和B(x2,0)两点,其中x1<x2
(1)求m的取值范围;
(2)若x12+x22=10,求抛物线的解析式,并在平面直角坐标系中画出这条抛物线;
(3)设这条抛物线的顶点坐标为C,延长CA交y轴于点D。在y轴上是否存在点P,使以P、O、B为顶点的三角形与△BCD相似?若存在,求出P点的坐标;若不存在,请说明理由。例4: 一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m)。已知物体竖直上抛运动中,h=v0t- ? gt2(v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s2)。问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m?地面例4:解:由题意,得h关于t的二次函数
解析式为h=10t-5t2取h=0,得一元二次方程
10t-5t2=0解方程得t1=0;t2=2球从弹起至回到地面需要时间为t2-t1=2(s)取h=3.75,得一元二次方程10t-5t2=3.75解方程得t1=0.5;t2=1.5答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m。
?10米10米若此隧道是双向车道,那么这辆货车又能否顺利经过隧道?
探究如图是一个汽车隧道,形状成抛物线,隧道路面宽10米,顶部到地面的距离为10米.高4米,宽4米的一辆厢式货车能否顺利经过这条单向行车的隧道?
?10米10米若此隧道是双向车道,那么这辆货车又能否顺利经过隧道?
已知二次函数y=x2+4x+3,回答下列问题:
(1)说出此抛物线的对称轴 和顶点坐标 ;
(2)抛物线与x轴的交点A、B
的坐标,与y轴的交点C的坐标;
(3)函数的最值和增减性;
(4)x取何值时① y<0 ;②y>0
xyABOCX=-2(-3,0)(-1,0)(-2,-1)(0,3) 说一说二次函数的性质y=a(x+m)2+ky=ax2+bx+cy=a(x-x1)(x-x2)直线x=-m直线x=直线x=(-m,k)( ) 当x≤-m时,y随x的增大而减小;当x≥-m时,y随x的增大而增大当x ≤ 时,y随x的增大而减小;当x ≥ 时y随x的增大而增大当x≤-m时,y随的增大而增大;当x≥-m时,y随的增大而减小当x≤ 时,y随x的增大而增大;当x≥ 时y随x的增大而减小当 x=-m 时,y最小值=k当x= 时,y最小值=当x=-m时,y最大值=k当x= 时,y最大值=yxooyx1、若抛物线y=ax2+3x-4与抛物线y=-2x2形状相同,则a= .2、二次函数y=x2+1的图象的顶点坐标是 .3、二次函数y=ax2+bx+c的图象与x轴的两个交点分别为A(1,0),B(-3,0)则它的对称轴是 .4、二次函数y=x2-2x+2 当x= 时,y的最小值为 .5、二次函数y=4x2+mx+1的图象顶点在x轴上,则m= ;若它的顶点在y轴上,则m= .±2(0,1)直线x=-111±40X=1、抛物线y=ax2+bx+c如图所示,则( )
(A)a>0,b>0,c>0 (B)a>0,b<0,c<0
(c)a>0,b>0,c<0 (D)a>0,b<0,c>0
2、已知二次函数y=ax2+bx+c的图象如图所示,下列结论中,正确的个数是 ( )
①a+b+c<0②a-b+c>0③abc>0④b=2a
(A) 4 (B) 3 (C) 2 (D) 1xyxyX=-10(2)(1)BC1A看方向 (上正、下负)看交点 (上正、下负)二次函数的图象看对称轴(左同、右异) 开启 智慧
你说 我说1、函数y=ax2+bx+c的图象如图所示。X= 为该函数图象的对称轴,根据这个函数图象,你能得到关于该函数的哪些性质和结论?xyX=o-11-1例:已知抛物线y=x2+(2n-1)x+n2-1(n为常数)
(1)当该抛物线经过坐标原点,并且顶点在第四象限时,求出它所对应的函数解析式;
(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点,过A作x轴的平行线,交抛物线于另一点D,再作AB⊥x轴于B,DC⊥x轴于C。
①当BC=1时,求矩形ABCD的周长;
②试问矩形ABCD的周长是否存在最大值?如果存在,请你求出这个最大值,并指出此时A点的坐标;如果不存在,请说出你的理由。 尝试拓展 发展思维?行家看“门道”(1)通过本节课的学习你对二次函数的图象与性质有什么的认识?
探究如图是一个汽车隧道,形状成抛物线,隧道路面宽10米,顶部到地面的距离为10米.高4米,宽4米的一辆厢式货车能否顺利经过这条单向行车的隧道?
?10米10米若此隧道是双向车道,那么这辆货车又能否顺利经过隧道?
探究如图是一个汽车隧道,形状成抛物线,隧道路面宽10米,顶部到地面的距离为10米.高4米,宽4米的一辆厢式货车能否顺利经过这条单向行车的隧道?
?10米10米若此隧道是双向车道,那么这辆货车又能否顺利经过隧道?
1、已知对于x的所有实数,函数y=x2-4kx+2k+30的值均为非负数,化简:2、已知抛物线y=(m-1)x2+4x-3开口向上,与x轴相交于A(x1,0)和B(x2,0)两点,其中x1<x2
(1)求m的取值范围;
(2)若x12+x22=10,求抛物线的解析式,并在平面直角坐标系中画出这条抛物线;
(3)设这条抛物线的顶点坐标为C,延长CA交y轴于点D。在y轴上是否存在点P,使以P、O、B为顶点的三角形与△BCD相似?若存在,求出P点的坐标;若不存在,请说明理由。例4: 一个球从地面上竖直向上弹起时的速度为10m/s,经过t(s)时球的高度为h(m)。已知物体竖直上抛运动中,h=v0t- ? gt2(v0表示物体运动上弹开始时的速度,g表示重力系数,取g=10m/s2)。问球从弹起至回到地面需要多少时间?经多少时间球的高度达到3.75m?地面例4:解:由题意,得h关于t的二次函数
解析式为h=10t-5t2取h=0,得一元二次方程
10t-5t2=0解方程得t1=0;t2=2球从弹起至回到地面需要时间为t2-t1=2(s)取h=3.75,得一元二次方程10t-5t2=3.75解方程得t1=0.5;t2=1.5答:球从弹起至回到地面需要时间为2(s);
经过圆心的0.5s或1.5s球的高度达到3.75m。
同课章节目录
