【浙教版七上同步练习】 第五章一元一次方程检测题(能力提升)(含答案)
文档属性
| 名称 | 【浙教版七上同步练习】 第五章一元一次方程检测题(能力提升)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-25 14:24:16 | ||
图片预览



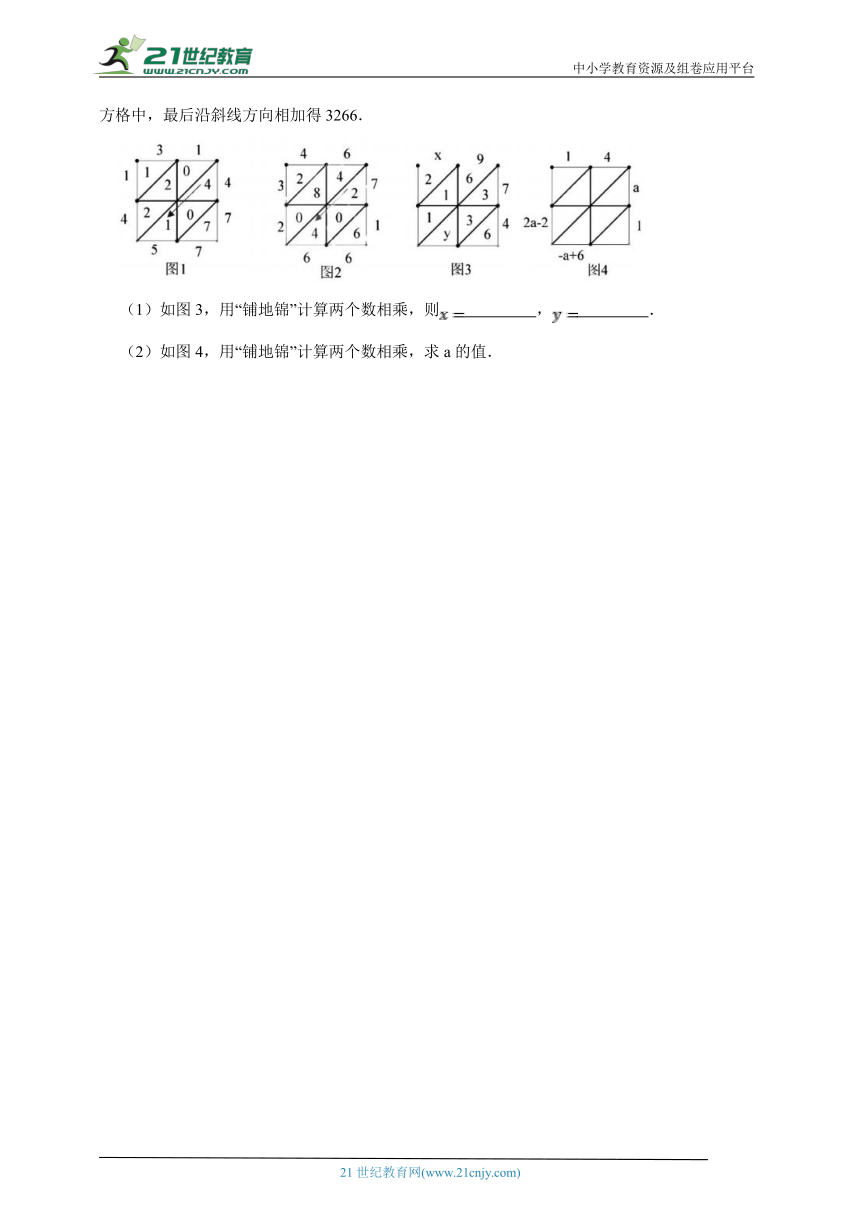
文档简介
中小学教育资源及组卷应用平台
【浙教版七上同步练习】
第五章一元一次方程检测题(能力提升)
一、单选题
1.长沙是中国男足的福地,3月23日中国队1:0胜韩国队,赢得12强赛的首场胜利!已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一对打了14场比赛,负了5场,共得23分,那么这个队胜了( )
A.5场 B.6场 C.7场 D.8场
2.在元旦前夕美化校园的活动中,七年级先安排31人去捡垃圾,18人去扫地,后又增派20人去支援他们,增援后捡垃圾的人数是扫地人数的2倍,求支援捡垃圾和扫地的人数分别有多少人,若设支援捡垃圾的有x人,则根据题意列出的方程是( )
A.31+x=2×18 B.31+x=2(38﹣x)
C.51﹣x=2(18+x) D.51﹣x=2×18
3.有一批画册,若3人合看一本,则多余2本;若2人合看一本,就有9人没有,设人数为x,则列出的方程是( )
A.3x+2=2x﹣9 B. ﹣2=
C. +2= D. +2= ﹣9
4.解方程时,去分母后可以得到( )
A.1﹣x﹣3=3x B.6﹣2x﹣6=3x
C.6﹣x+3=3x D.1﹣x+3=3x
5.阅读:关于x方程ax=b在不同的条件下解的情况如下:(1)当a≠0时,有唯一解x= ;(2)当a=0,b=0时有无数解;(3)当a=0,b≠0时无解.请你根据以上知识作答:已知关于x的方程 a= ﹣ (x﹣6)无解,则a的值是( )
A.1 B.﹣1 C.±1 D.a≠1
二、填空题
6.根据下列各题的条件,写出仍然成立的等式.
(1)a+2=b,两边都减去2. .
(2),两边都乘以30. .
(3)3x=12y,两边都除以3. .
7.已知2x-1与4-x的值互为相反数,则x的值是
8.关于x的方程ax+1=4的解是x=1,则a= .
9.将等式3x﹣2y=7变形成用y的代数式表示x= .
10.一年定期存款的年利率为1.98%,到期取款时须扣除利息的20%作为利息税上缴国库. 假若小颖存一笔一年定期储蓄,到期扣除利息税后实得利息158.4元,那么她存入的人民币是 .
11.方程 的解是 .
三、计算题
12.解方程
(1);
(2).
13.解方程: .
14.解方程: .
四、解答题
15.等式(k-2)x2+kx+1=0是关于x的一元一次方程(即x未知),求这个方程的解.
16.已知关于x的方程,解答下列问题:
(1)如果方程的解是x=-11时,求字母a的值.
(2)如果某同学在解此方程去分母时,方程右边的(-1)没有乘以6,结果求得解是x=-2,求字母a的值.
(3)如果方程无解,请你直接写出字母a的值.
五、综合题
17.解方程.
(1)3(2x-1)=4x+3
(2)
18.公园门票价格规定如下表:
购票张数 1~50张 51~100张 100张以上
每张票的价格 15元 13元 11元
某校七年级(1)(2)两个班共102人去游园,其中(1)班超过40人,不足50人,经估算,如果两个班都以班为单位购票,则一共应付1422元.问:
(1)两个班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可比两个班都以班为单位购票省多少元钱?
(3)如果七年级(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
19.温州和杭州某厂同时生产某种型号的机器若干台,温州厂可支援外地10台,杭州厂可支援外地4台,现在决定给武汉8台,南昌6台,每台机器的运费如下表,设杭州厂运往南昌的机器为x台,
(1)用含x的代数式来表示总运费(单位:元)
(2)若总运费为8400元,则杭州厂运往南昌的机器应为多少台
(3)试问有无可能使总运费是7800元?若有可能请写出相应的调动方案;若无可能,请说明理由.
六、实践探究题
20.阅读下列材料,并完成相应的任务.
我国明朝数学家程大位所著的《算法统宗》中介绍了一种计算乘法的方法,称为“铺地锦”如图1所示,计算31×47,首先把乘数31和47分别写在方格的上面和右面,然后以31的每位数字分别乘以47的每位数字,将结果计入对应的格子中(如图1,12写在3下面的方格里,十位1写在斜线的上面,个位2写在斜线的下面),再把同一斜线上的数相加,结果写在斜线末端,最后把得数依次写下来时1457,即31×47=1457.如图2,计算46×71,将乘数46写在方格上边,乘数71写在方格右边,然后用乘数46的每位数字乘以乘数71的每位数字,将结果计入相应的方格中,最后沿斜线方向相加得3266.
(1)如图3,用“铺地锦”计算两个数相乘,则 , .
(2)如图4,用“铺地锦”计算两个数相乘,求a的值.
答案解析部分
1.【答案】C
【知识点】一元一次方程的实际应用-积分问题
2.【答案】B
【知识点】一元一次方程的实际应用-和差倍分问题
3.【答案】C
【知识点】列一元一次方程
4.【答案】B
【知识点】解一元一次方程
5.【答案】A
【知识点】解一元一次方程
6.【答案】(1)a=b-2
(2)6x=5y
(3)x=4y
【知识点】等式的性质
7.【答案】-3
【知识点】相反数及有理数的相反数;一元一次方程的其他应用
8.【答案】3
【知识点】一元一次方程的解
9.【答案】
【知识点】等式的性质
10.【答案】10000元
【知识点】一元一次方程的其他应用
11.【答案】1
【知识点】解一元一次方程
12.【答案】(1)解:,
去括号得2x﹣4﹣1+3x=x+3,
移项得:2x+3x﹣x=3+4+1,
合并得:4x=8,
系数化1得:x=2;
(2)解:,
去分母得:,
去括号得:,
移项合并得:,
系数化1得:.
【知识点】解含括号的一元一次方程;解含分数系数的一元一次方程
13.【答案】解:去分母: ,
去括号: ,
移项: ,
合并同类项: ,
把x系数化为1: .
【知识点】解含括号的一元一次方程;解含分数系数的一元一次方程
14.【答案】解:原方程可化为 ,去分母,得4(3x+7)-3(2x-3)=24,去括号,得12x+28-6x+9=24,移项,合并同类项,得6x=-13,系数化为1, .
【知识点】解含分数系数的一元一次方程
15.【答案】解:由题意可得:k-2=0,
两边同时加2,得k=2,
则原方程为:2x+1=0,
两边同时减去1,得2x=-1,
两边同时除以2,得x=- .
【知识点】一元一次方程的定义;利用等式的性质解一元一次方程
16.【答案】(1)解:∵方程的解是x=-11,
∴,
∴.
(2)解:∵某同学在解此方程去分母时,方程右边的(-1)没有乘以6,
∴该同学去分母后得到的方程为:,
∵解是x=-2,
∴
∴.
(3)解:原方程去分母得:,
∴
∵方程无解,
∴.
【知识点】一元一次方程的解;解含分数系数的一元一次方程
17.【答案】(1)解:6x 3 4x 3
6x 4x 3 3
2x 6
x 3
(2)解:3(2 x) 18 2x (2x 3)
6 3x 18 2x 2x 3
3x 2x 2x 3 6 18
3x 9
x 3
【知识点】解一元一次方程
18.【答案】(1)解:设七年级(1)班的学生人数为x人,则七年级(2)班的学生人数为 人
由题意可得:
解得:
则
答:七年级(1)班有48名学生,七年级(2)班有54名学生
(2)解:两班联合起来购票 应付钱数为: (元)
则可省的钱数为: (元)
答:如果两班联合起来,作为一个团体购票,可省300元
(3)解: (元), (元)
因为
所以如果七年级(1)班单独组织去游园,组织者直接购买51张门票最省钱.
【知识点】一元一次方程的实际应用-方案选择问题
19.【答案】(1)解:总费用为:400(6-x)+800(4+x)+300x +500(4-x)=200x+7600
(2)解:由题意得200x+7600=8400,解得x=4,
答:杭州运往南昌的机器应为4台
(3)解:由题意得200x+7600=7800,
解得x=1. 符合实际意义,
答: 有可能 ,杭州厂运往南昌的机器为1台.
【知识点】一元一次方程的其他应用
20.【答案】(1)3;2
(2)解:根据题意,填好图4,如图,
,
由题意可得4a=10(a-2)+(-a+5),解得,a=3.
【知识点】一元一次方程的实际应用-古代数学问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【浙教版七上同步练习】
第五章一元一次方程检测题(能力提升)
一、单选题
1.长沙是中国男足的福地,3月23日中国队1:0胜韩国队,赢得12强赛的首场胜利!已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一对打了14场比赛,负了5场,共得23分,那么这个队胜了( )
A.5场 B.6场 C.7场 D.8场
2.在元旦前夕美化校园的活动中,七年级先安排31人去捡垃圾,18人去扫地,后又增派20人去支援他们,增援后捡垃圾的人数是扫地人数的2倍,求支援捡垃圾和扫地的人数分别有多少人,若设支援捡垃圾的有x人,则根据题意列出的方程是( )
A.31+x=2×18 B.31+x=2(38﹣x)
C.51﹣x=2(18+x) D.51﹣x=2×18
3.有一批画册,若3人合看一本,则多余2本;若2人合看一本,就有9人没有,设人数为x,则列出的方程是( )
A.3x+2=2x﹣9 B. ﹣2=
C. +2= D. +2= ﹣9
4.解方程时,去分母后可以得到( )
A.1﹣x﹣3=3x B.6﹣2x﹣6=3x
C.6﹣x+3=3x D.1﹣x+3=3x
5.阅读:关于x方程ax=b在不同的条件下解的情况如下:(1)当a≠0时,有唯一解x= ;(2)当a=0,b=0时有无数解;(3)当a=0,b≠0时无解.请你根据以上知识作答:已知关于x的方程 a= ﹣ (x﹣6)无解,则a的值是( )
A.1 B.﹣1 C.±1 D.a≠1
二、填空题
6.根据下列各题的条件,写出仍然成立的等式.
(1)a+2=b,两边都减去2. .
(2),两边都乘以30. .
(3)3x=12y,两边都除以3. .
7.已知2x-1与4-x的值互为相反数,则x的值是
8.关于x的方程ax+1=4的解是x=1,则a= .
9.将等式3x﹣2y=7变形成用y的代数式表示x= .
10.一年定期存款的年利率为1.98%,到期取款时须扣除利息的20%作为利息税上缴国库. 假若小颖存一笔一年定期储蓄,到期扣除利息税后实得利息158.4元,那么她存入的人民币是 .
11.方程 的解是 .
三、计算题
12.解方程
(1);
(2).
13.解方程: .
14.解方程: .
四、解答题
15.等式(k-2)x2+kx+1=0是关于x的一元一次方程(即x未知),求这个方程的解.
16.已知关于x的方程,解答下列问题:
(1)如果方程的解是x=-11时,求字母a的值.
(2)如果某同学在解此方程去分母时,方程右边的(-1)没有乘以6,结果求得解是x=-2,求字母a的值.
(3)如果方程无解,请你直接写出字母a的值.
五、综合题
17.解方程.
(1)3(2x-1)=4x+3
(2)
18.公园门票价格规定如下表:
购票张数 1~50张 51~100张 100张以上
每张票的价格 15元 13元 11元
某校七年级(1)(2)两个班共102人去游园,其中(1)班超过40人,不足50人,经估算,如果两个班都以班为单位购票,则一共应付1422元.问:
(1)两个班各有多少学生?
(2)如果两个班联合起来,作为一个团体购票,可比两个班都以班为单位购票省多少元钱?
(3)如果七年级(1)班单独组织去游园,作为组织者的你如何购票才最省钱?
19.温州和杭州某厂同时生产某种型号的机器若干台,温州厂可支援外地10台,杭州厂可支援外地4台,现在决定给武汉8台,南昌6台,每台机器的运费如下表,设杭州厂运往南昌的机器为x台,
(1)用含x的代数式来表示总运费(单位:元)
(2)若总运费为8400元,则杭州厂运往南昌的机器应为多少台
(3)试问有无可能使总运费是7800元?若有可能请写出相应的调动方案;若无可能,请说明理由.
六、实践探究题
20.阅读下列材料,并完成相应的任务.
我国明朝数学家程大位所著的《算法统宗》中介绍了一种计算乘法的方法,称为“铺地锦”如图1所示,计算31×47,首先把乘数31和47分别写在方格的上面和右面,然后以31的每位数字分别乘以47的每位数字,将结果计入对应的格子中(如图1,12写在3下面的方格里,十位1写在斜线的上面,个位2写在斜线的下面),再把同一斜线上的数相加,结果写在斜线末端,最后把得数依次写下来时1457,即31×47=1457.如图2,计算46×71,将乘数46写在方格上边,乘数71写在方格右边,然后用乘数46的每位数字乘以乘数71的每位数字,将结果计入相应的方格中,最后沿斜线方向相加得3266.
(1)如图3,用“铺地锦”计算两个数相乘,则 , .
(2)如图4,用“铺地锦”计算两个数相乘,求a的值.
答案解析部分
1.【答案】C
【知识点】一元一次方程的实际应用-积分问题
2.【答案】B
【知识点】一元一次方程的实际应用-和差倍分问题
3.【答案】C
【知识点】列一元一次方程
4.【答案】B
【知识点】解一元一次方程
5.【答案】A
【知识点】解一元一次方程
6.【答案】(1)a=b-2
(2)6x=5y
(3)x=4y
【知识点】等式的性质
7.【答案】-3
【知识点】相反数及有理数的相反数;一元一次方程的其他应用
8.【答案】3
【知识点】一元一次方程的解
9.【答案】
【知识点】等式的性质
10.【答案】10000元
【知识点】一元一次方程的其他应用
11.【答案】1
【知识点】解一元一次方程
12.【答案】(1)解:,
去括号得2x﹣4﹣1+3x=x+3,
移项得:2x+3x﹣x=3+4+1,
合并得:4x=8,
系数化1得:x=2;
(2)解:,
去分母得:,
去括号得:,
移项合并得:,
系数化1得:.
【知识点】解含括号的一元一次方程;解含分数系数的一元一次方程
13.【答案】解:去分母: ,
去括号: ,
移项: ,
合并同类项: ,
把x系数化为1: .
【知识点】解含括号的一元一次方程;解含分数系数的一元一次方程
14.【答案】解:原方程可化为 ,去分母,得4(3x+7)-3(2x-3)=24,去括号,得12x+28-6x+9=24,移项,合并同类项,得6x=-13,系数化为1, .
【知识点】解含分数系数的一元一次方程
15.【答案】解:由题意可得:k-2=0,
两边同时加2,得k=2,
则原方程为:2x+1=0,
两边同时减去1,得2x=-1,
两边同时除以2,得x=- .
【知识点】一元一次方程的定义;利用等式的性质解一元一次方程
16.【答案】(1)解:∵方程的解是x=-11,
∴,
∴.
(2)解:∵某同学在解此方程去分母时,方程右边的(-1)没有乘以6,
∴该同学去分母后得到的方程为:,
∵解是x=-2,
∴
∴.
(3)解:原方程去分母得:,
∴
∵方程无解,
∴.
【知识点】一元一次方程的解;解含分数系数的一元一次方程
17.【答案】(1)解:6x 3 4x 3
6x 4x 3 3
2x 6
x 3
(2)解:3(2 x) 18 2x (2x 3)
6 3x 18 2x 2x 3
3x 2x 2x 3 6 18
3x 9
x 3
【知识点】解一元一次方程
18.【答案】(1)解:设七年级(1)班的学生人数为x人,则七年级(2)班的学生人数为 人
由题意可得:
解得:
则
答:七年级(1)班有48名学生,七年级(2)班有54名学生
(2)解:两班联合起来购票 应付钱数为: (元)
则可省的钱数为: (元)
答:如果两班联合起来,作为一个团体购票,可省300元
(3)解: (元), (元)
因为
所以如果七年级(1)班单独组织去游园,组织者直接购买51张门票最省钱.
【知识点】一元一次方程的实际应用-方案选择问题
19.【答案】(1)解:总费用为:400(6-x)+800(4+x)+300x +500(4-x)=200x+7600
(2)解:由题意得200x+7600=8400,解得x=4,
答:杭州运往南昌的机器应为4台
(3)解:由题意得200x+7600=7800,
解得x=1. 符合实际意义,
答: 有可能 ,杭州厂运往南昌的机器为1台.
【知识点】一元一次方程的其他应用
20.【答案】(1)3;2
(2)解:根据题意,填好图4,如图,
,
由题意可得4a=10(a-2)+(-a+5),解得,a=3.
【知识点】一元一次方程的实际应用-古代数学问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
