【浙教版七上同步练习】 6.9直线的相交(含答案)
文档属性
| 名称 | 【浙教版七上同步练习】 6.9直线的相交(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-25 17:41:43 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【浙教版七上同步练习】
6.9直线的相交
一、单选题
1.下列各图中,与互为余角的是( )
A. B. C. D.
2.已知点为直线外一点,点、、为直线上的三点,,,,则点到直线的距离为( )
A.等于2 B.小于2 C.大于2 D.不大于2
3.点P为直线l外一点,点A、B、C为l上三点,PA=5cm,PB=6cm,PC=6cm,则点P到直线l的距离是( )
A.5cm B.小于5cm C.不大于5cm D.7cm
二、填空题
4.如图,直线a、b相交于点O,若∠1=30°,则∠2=
5.如图,计划把河水引到水池A中,先引AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是
6.如图,点P是直线l外一点,过点P作于点O,点A是直线l上任意一点,连接,若,则的长可能是 (写出一个即可).
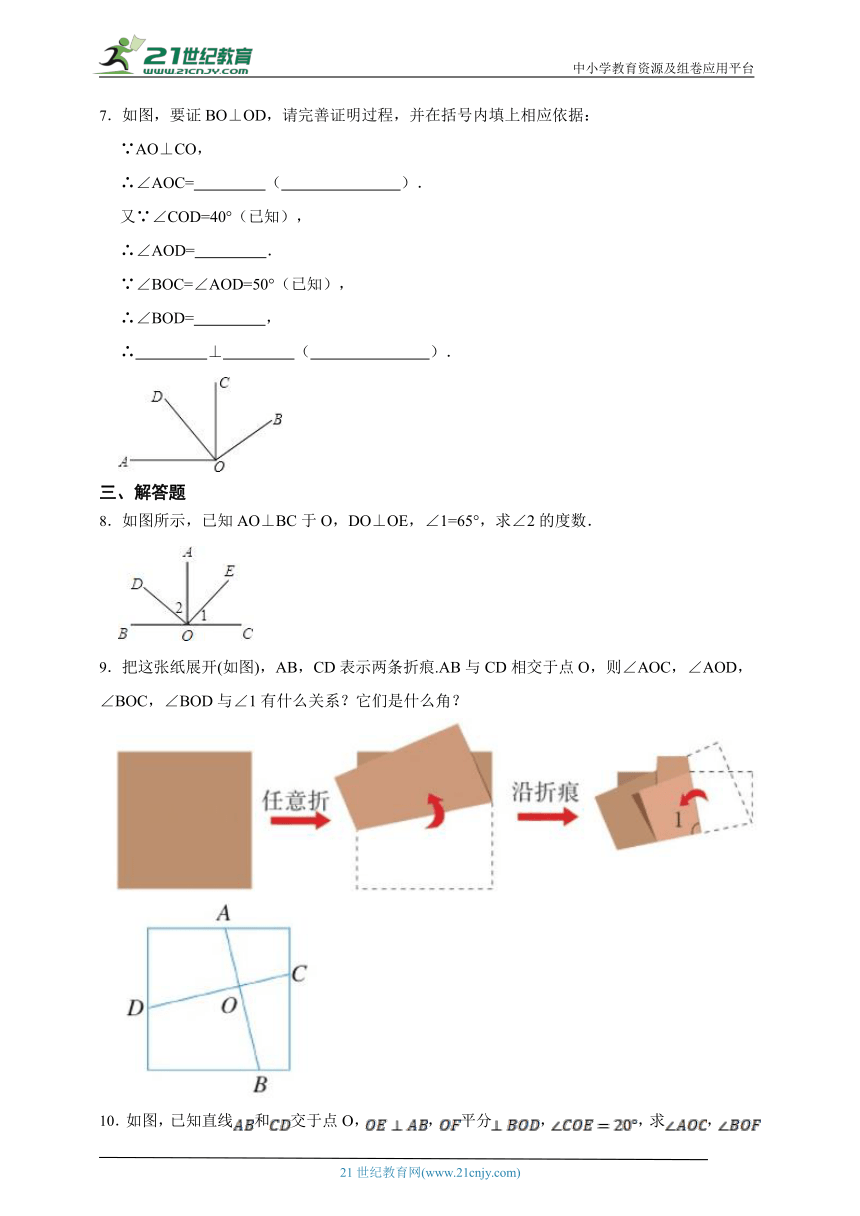
7.如图,要证BO⊥OD,请完善证明过程,并在括号内填上相应依据:
∵AO⊥CO,
∴∠AOC= ( ).
又∵∠COD=40°(已知),
∴∠AOD= .
∵∠BOC=∠AOD=50°(已知),
∴∠BOD= ,
∴ ⊥ ( ).
三、解答题
8.如图所示,已知AO⊥BC于O,DO⊥OE,∠1=65°,求∠2的度数.
9.把这张纸展开(如图),AB,CD表示两条折痕.AB与CD相交于点O,则∠AOC,∠AOD,∠BOC,∠BOD与∠1有什么关系?它们是什么角?
10.如图,已知直线和交于点O,,平分,,求,的度数.
四、作图题
11.如图,在中,,,平分交于点D.
(1)尺规作图:在中,作边上的高(保留痕迹,不写作法);
(2)在(1)的条件下,求的度数.
五、综合题
12.如图,在正方形网格中画有一段笔直的铁路及道口A,B和村庄M,N.完成以下作图.
(1)若在村庄N与道口A之间修一条最短的公路,在图中画出此公路,并说明这样画的理由;
(2)若在公路上选择一个地点P安装实时监控系统,要求点P到村庄N与道口B的距离相等,在图中标出点P的位置;
(3)当一节火车头行驶至铁路上的点Q时,距离村庄N最近.在图中确定点Q的位置(保留作图痕迹);
(4)若在道口A或B处修建一座火车站,使得到两村的距离和较短,应该修在 处.
13.如图,点P是∠AOB的边OB上的一点.
(1)过点P画OB的垂线,交OA于点C,
(2)过点P画OA的垂线,垂足为H,
(3)线段PH的长度是点P到 的距离,线段 是点C到直线OB的距离.
(4)因为直线外一点到直线上各点连接的所有线中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 (用“<”号连接)
14.如图,直线 , 相交于点 , 平分 .
(1)若 ,求 的度数.
(2)若 ,判断射线 , 的位置关系并说明理由.
15.我们知道两直线交于一点,对顶角有2对,三条直线交于一点,对顶角有6对,四条直线交于一点,对顶角有12对,…
(1)10条直线交于一点,对顶角有多少对?
(2)n(n≥2)条直线交于一点,对顶角有多少对?
答案解析部分
1.【答案】C
【知识点】余角、补角及其性质;对顶角及其性质
2.【答案】D
【知识点】点到直线的距离
3.【答案】C
【知识点】点到直线的距离
4.【答案】150°
【知识点】对顶角及其性质
5.【答案】垂线段最短
【知识点】垂线段最短
6.【答案】4
【知识点】垂线段最短
7.【答案】90°;垂直的定义;50°;90°;BO;OD;垂直的定义
【知识点】垂线
8.【答案】解:∵AO⊥BC于O,
∴∠AOC=90°,
又∠1=65°,
∴∠AOE=90°﹣65°=25°.
∵DO⊥OE,
∴∠DOE=90°,
∴∠2=∠DOE﹣∠AOE=90°﹣25°=65°
【知识点】垂线
9.【答案】解:相等关系,都是直角.
【知识点】垂线
10.【答案】解:∵,
∴.
∵,
∴,
∴.
∵平分,
∴.
【知识点】余角、补角及其性质;对顶角及其性质;角平分线的定义
11.【答案】(1)解:如图,为BC边上的高,
(2)解:在中,,
又,,
∴
∵平分,
∴
∵
∴
∴
∴.
【知识点】作图-垂线;角平分线的定义
12.【答案】(1)解:理由:两点之间线段最短.
(2)解:如图,
(3)解:如图,
(4)B
【知识点】线段的性质:两点之间线段最短;垂线段最短;线段的中点
13.【答案】(1)解:如图:
(2)解:如图:
(3)直线0A;PC的长
(4)PH<PC<OC.
【知识点】垂线段最短;点到直线的距离;作图-垂线
14.【答案】(1)解:∵ 平分 且 ,
∴ ,
∴
(2)解:射线 , 的位置关系是垂直.理由如下:
∵ 平分 ,
∴ ,
又∵ ,
∴ ,
∵ ,
∴ ,
∴ .
【知识点】垂线;对顶角及其性质;角平分线的定义
15.【答案】(1)【解答】如图①两条直线交于一点,图中共有 =2对对顶角;如图②三条直线交于一点,图中共有 =6对对顶角;如图③四条直线交于一点,图中共有 =12对对顶角;
…;
按这样的规律,10条直线交于一点,那么对顶角共有: =90,
故答案为:90
(2)【解答】由(1)得:n(n≥2)条直线交于一点,对顶角有: =n(n﹣1).
故答案为:n(n﹣1).
【知识点】对顶角及其性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【浙教版七上同步练习】
6.9直线的相交
一、单选题
1.下列各图中,与互为余角的是( )
A. B. C. D.
2.已知点为直线外一点,点、、为直线上的三点,,,,则点到直线的距离为( )
A.等于2 B.小于2 C.大于2 D.不大于2
3.点P为直线l外一点,点A、B、C为l上三点,PA=5cm,PB=6cm,PC=6cm,则点P到直线l的距离是( )
A.5cm B.小于5cm C.不大于5cm D.7cm
二、填空题
4.如图,直线a、b相交于点O,若∠1=30°,则∠2=
5.如图,计划把河水引到水池A中,先引AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是
6.如图,点P是直线l外一点,过点P作于点O,点A是直线l上任意一点,连接,若,则的长可能是 (写出一个即可).
7.如图,要证BO⊥OD,请完善证明过程,并在括号内填上相应依据:
∵AO⊥CO,
∴∠AOC= ( ).
又∵∠COD=40°(已知),
∴∠AOD= .
∵∠BOC=∠AOD=50°(已知),
∴∠BOD= ,
∴ ⊥ ( ).
三、解答题
8.如图所示,已知AO⊥BC于O,DO⊥OE,∠1=65°,求∠2的度数.
9.把这张纸展开(如图),AB,CD表示两条折痕.AB与CD相交于点O,则∠AOC,∠AOD,∠BOC,∠BOD与∠1有什么关系?它们是什么角?
10.如图,已知直线和交于点O,,平分,,求,的度数.
四、作图题
11.如图,在中,,,平分交于点D.
(1)尺规作图:在中,作边上的高(保留痕迹,不写作法);
(2)在(1)的条件下,求的度数.
五、综合题
12.如图,在正方形网格中画有一段笔直的铁路及道口A,B和村庄M,N.完成以下作图.
(1)若在村庄N与道口A之间修一条最短的公路,在图中画出此公路,并说明这样画的理由;
(2)若在公路上选择一个地点P安装实时监控系统,要求点P到村庄N与道口B的距离相等,在图中标出点P的位置;
(3)当一节火车头行驶至铁路上的点Q时,距离村庄N最近.在图中确定点Q的位置(保留作图痕迹);
(4)若在道口A或B处修建一座火车站,使得到两村的距离和较短,应该修在 处.
13.如图,点P是∠AOB的边OB上的一点.
(1)过点P画OB的垂线,交OA于点C,
(2)过点P画OA的垂线,垂足为H,
(3)线段PH的长度是点P到 的距离,线段 是点C到直线OB的距离.
(4)因为直线外一点到直线上各点连接的所有线中,垂线段最短,所以线段PC、PH、OC这三条线段大小关系是 (用“<”号连接)
14.如图,直线 , 相交于点 , 平分 .
(1)若 ,求 的度数.
(2)若 ,判断射线 , 的位置关系并说明理由.
15.我们知道两直线交于一点,对顶角有2对,三条直线交于一点,对顶角有6对,四条直线交于一点,对顶角有12对,…
(1)10条直线交于一点,对顶角有多少对?
(2)n(n≥2)条直线交于一点,对顶角有多少对?
答案解析部分
1.【答案】C
【知识点】余角、补角及其性质;对顶角及其性质
2.【答案】D
【知识点】点到直线的距离
3.【答案】C
【知识点】点到直线的距离
4.【答案】150°
【知识点】对顶角及其性质
5.【答案】垂线段最短
【知识点】垂线段最短
6.【答案】4
【知识点】垂线段最短
7.【答案】90°;垂直的定义;50°;90°;BO;OD;垂直的定义
【知识点】垂线
8.【答案】解:∵AO⊥BC于O,
∴∠AOC=90°,
又∠1=65°,
∴∠AOE=90°﹣65°=25°.
∵DO⊥OE,
∴∠DOE=90°,
∴∠2=∠DOE﹣∠AOE=90°﹣25°=65°
【知识点】垂线
9.【答案】解:相等关系,都是直角.
【知识点】垂线
10.【答案】解:∵,
∴.
∵,
∴,
∴.
∵平分,
∴.
【知识点】余角、补角及其性质;对顶角及其性质;角平分线的定义
11.【答案】(1)解:如图,为BC边上的高,
(2)解:在中,,
又,,
∴
∵平分,
∴
∵
∴
∴
∴.
【知识点】作图-垂线;角平分线的定义
12.【答案】(1)解:理由:两点之间线段最短.
(2)解:如图,
(3)解:如图,
(4)B
【知识点】线段的性质:两点之间线段最短;垂线段最短;线段的中点
13.【答案】(1)解:如图:
(2)解:如图:
(3)直线0A;PC的长
(4)PH<PC<OC.
【知识点】垂线段最短;点到直线的距离;作图-垂线
14.【答案】(1)解:∵ 平分 且 ,
∴ ,
∴
(2)解:射线 , 的位置关系是垂直.理由如下:
∵ 平分 ,
∴ ,
又∵ ,
∴ ,
∵ ,
∴ ,
∴ .
【知识点】垂线;对顶角及其性质;角平分线的定义
15.【答案】(1)【解答】如图①两条直线交于一点,图中共有 =2对对顶角;如图②三条直线交于一点,图中共有 =6对对顶角;如图③四条直线交于一点,图中共有 =12对对顶角;
…;
按这样的规律,10条直线交于一点,那么对顶角共有: =90,
故答案为:90
(2)【解答】由(1)得:n(n≥2)条直线交于一点,对顶角有: =n(n﹣1).
故答案为:n(n﹣1).
【知识点】对顶角及其性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
