【浙教版八上同步练习】 1.2定义与命题(含答案)
文档属性
| 名称 | 【浙教版八上同步练习】 1.2定义与命题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 653.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-26 13:56:56 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【浙教版八上同步练习】
1.2定义与命题
一、单选题
1.下列命题中,是假命题的是( )
A.两点之间,线段最短 B.同旁内角互补
C.直角的补角仍然是直角 D.垂线段最短
2.下列命题正确的是:( )
①同位角相等,两直线平行;②相等的两个角是对顶角;③同旁内角互补;④在同一平面内,过一点有且只有一条直线与已知直线垂直.
A.①③④ B.①③ C.①④ D.②③
3.下列命题中:①.有理数和数轴上的点一一对应;②.内错角相等;③.平行于同一条直线的两条直线互相平行;④.邻补角一定互补.其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
4.下列命题是真命题的是( )
A.同位角相等
B.两直线平行,同旁内角相等
C.同旁内角互补
D.平行于同一直线的两条直线平行
5.观察下列几个命题:①相等的角是对顶角;②同位角都相等;③三个角相等的三角形是等边三角形;④两直线平行,内错角相等;⑤若a2=b2,则a=b.其中真命题的个数有( )
A.0个 B.1个 C.2个 D.3个
二、填空题
6.命题“对顶角相等”的题设是 ;结论是 .
7.将命题“同角的补角相等”写成“如果......那么.....”的形式: .
8.把定理“有两个角互余的三角形是直角三角形”,写成“如果...那么...”的形式是:如果 , 那么 .
9. 在命题“两直线平行,同位角互补”中,“两直线平行”叫作“条件”,“同位角互补”叫作 .
三、解答题
10.下列各命题的条件是什么?结论是什么?
(1)两直线平行,同位角相等;
(2)过一点有且只有一条直线与已知直线平行.
11.把命题“同角的补角相等”改写成“如果……那么……“的形式.
12.以下是两位同学在复习不等式过程中的对话:
小明说:”不等式a> 2a永远都不会成立,因为如果在这个不等式两边同时除以a,就.会出现1>2这样的错误结论!”
小丽说:“如果a>b,c>d,那么一定会得出a-c>b-d."
你认为小明的说法 (填“正确”或“不正确”);小丽的说法 (填“正确”或“不正确”),并选择其中一个人判断阐述你的理由(若认为正确,则进行证明;若认为不正确,则给出反例).
四、作图题
13.阅读下面材料:
判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
例如要判断命题“相等的角是对顶角”是假命题,可以举出如下反例:
如图,OC是∠AOB的平分线,∠1=∠2,但它们不是对顶角.
请你举出一个反例说明命题“如果两个角的两边分别平行,那么这两个角相等”是假命题.(要求:画出相应的图形,并用文字语言或符号语言表述所举反例)
五、综合题
14.用“如果……那么……”的形式改写下列命题。
(1)两条平行线被第三条直线所截,则它们的一对同位角的平分线互相平行。
(2)菱形的四边相等。
15.写出下列命题的条件和结论.
(1)如果a2=b2,那么a=b;
(2)同角或等角的补角相等;
(3)同旁内角互补,两直线平行.
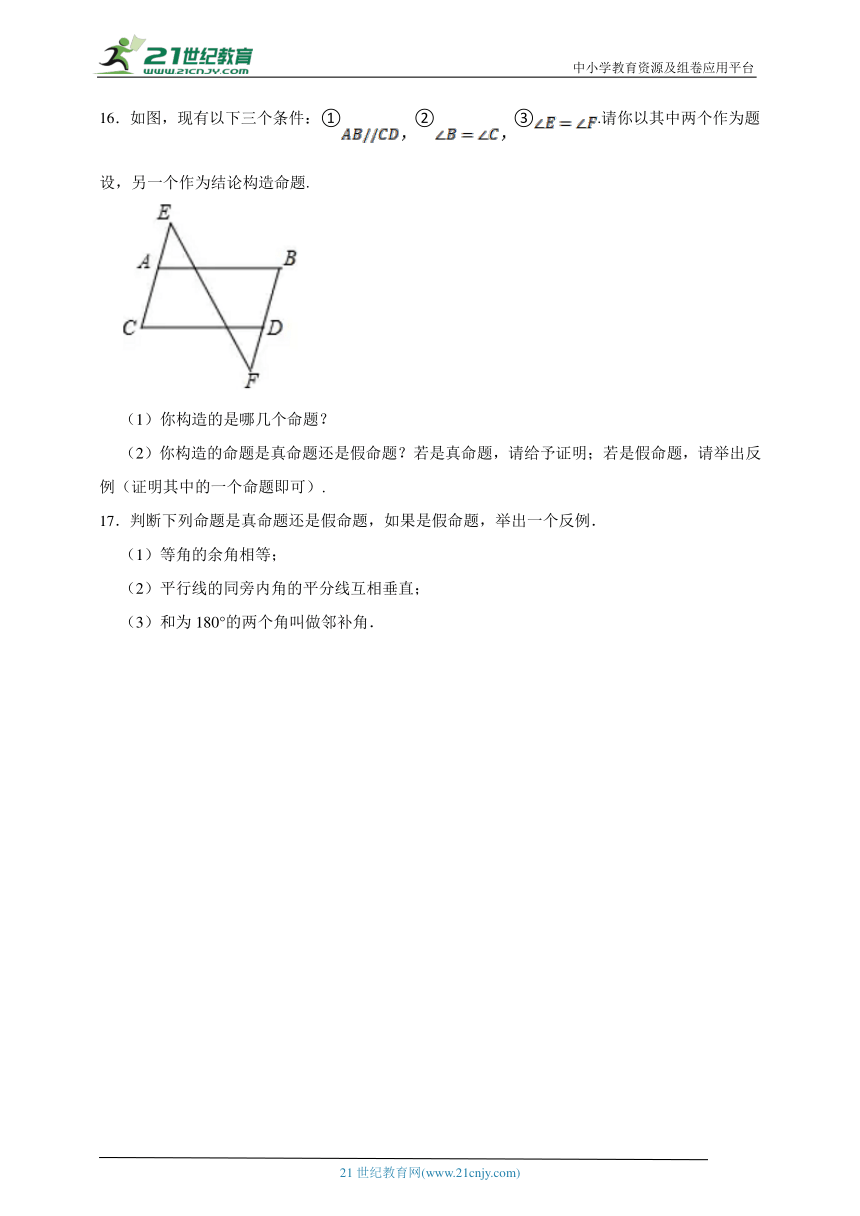
16.如图,现有以下三个条件:①②③.请你以其中两个作为题设,另一个作为结论构造命题.
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).
17.判断下列命题是真命题还是假命题,如果是假命题,举出一个反例.
(1)等角的余角相等;
(2)平行线的同旁内角的平分线互相垂直;
(3)和为180°的两个角叫做邻补角.
答案解析部分
1.【答案】B
【知识点】真命题与假命题
2.【答案】C
【知识点】真命题与假命题
3.【答案】B
【知识点】真命题与假命题
4.【答案】D
【知识点】真命题与假命题
5.【答案】C
【知识点】平行线的性质;真命题与假命题
6.【答案】两个角是对顶角;这两个角相等
【知识点】定义、命题及定理的概念
7.【答案】如果两个角是同一个角的补角,那么这两个角相等
【知识点】定义、命题及定理的概念
8.【答案】一个三角形的两个角互余;这个三角形是直角三角形
【知识点】定义、命题及定理的概念
9.【答案】结论
【知识点】定义、命题及定理的概念
10.【答案】(1)解:条件是两直线平行;结论是同位角相等。
(2)解:条件是直线外有一点,过这一点做一条直线和已知直线平行;结论是这样的平行线有且只有一条。
【知识点】定义、命题及定理的概念
11.【答案】解:如果两个角是同一个角的补角,那么这两个角相等
【知识点】定义、命题及定理的概念
12.【答案】不正确;不正确
【知识点】真命题与假命题
13.【答案】解:如图,
∠1+∠2=180°;
如果两个角的两边分别平行,那么这两个角相等或互补.
【知识点】真命题与假命题
14.【答案】(1)解:如果两条平行线被第三条直线所截 那么它们的一对同位角的平分线互相平行
(2)解:如果一个四边形是菱形 那么四边相等。
【知识点】定义、命题及定理的概念
15.【答案】(1)解:条件:a2=b2;结论:a=b
(2)解:条件:两个角是同角或等角的补角;结论:这两个角相等
(3)解:条件:同旁内角互补;结论:两直线平行。
【知识点】定义、命题及定理的概念
16.【答案】(1)解:有:如果那么;
如果那么;
如果,那么;
(2)解:如图:
∵AB∥CD,
∴∠B=∠CDF,
∵∠B=∠C,
∴∠C=∠CDF,
∴CE∥BF,
∴∠E=∠F,
∴如果那么为真命题;
∵AB∥CD,
∴∠B=∠CDF,
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∴∠B=∠C,
∴如果那么为真命题;
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∵∠B=∠C,
∴∠B=∠CDF,
∴AB∥CD,
∴如果,那么为真命题.
【知识点】定义、命题及定理的概念;真命题与假命题
17.【答案】(1)真命题;
(2)真命题;
(3)假命题,如两个不同书本上的两个和为180°的角.
【知识点】真命题与假命题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【浙教版八上同步练习】
1.2定义与命题
一、单选题
1.下列命题中,是假命题的是( )
A.两点之间,线段最短 B.同旁内角互补
C.直角的补角仍然是直角 D.垂线段最短
2.下列命题正确的是:( )
①同位角相等,两直线平行;②相等的两个角是对顶角;③同旁内角互补;④在同一平面内,过一点有且只有一条直线与已知直线垂直.
A.①③④ B.①③ C.①④ D.②③
3.下列命题中:①.有理数和数轴上的点一一对应;②.内错角相等;③.平行于同一条直线的两条直线互相平行;④.邻补角一定互补.其中真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
4.下列命题是真命题的是( )
A.同位角相等
B.两直线平行,同旁内角相等
C.同旁内角互补
D.平行于同一直线的两条直线平行
5.观察下列几个命题:①相等的角是对顶角;②同位角都相等;③三个角相等的三角形是等边三角形;④两直线平行,内错角相等;⑤若a2=b2,则a=b.其中真命题的个数有( )
A.0个 B.1个 C.2个 D.3个
二、填空题
6.命题“对顶角相等”的题设是 ;结论是 .
7.将命题“同角的补角相等”写成“如果......那么.....”的形式: .
8.把定理“有两个角互余的三角形是直角三角形”,写成“如果...那么...”的形式是:如果 , 那么 .
9. 在命题“两直线平行,同位角互补”中,“两直线平行”叫作“条件”,“同位角互补”叫作 .
三、解答题
10.下列各命题的条件是什么?结论是什么?
(1)两直线平行,同位角相等;
(2)过一点有且只有一条直线与已知直线平行.
11.把命题“同角的补角相等”改写成“如果……那么……“的形式.
12.以下是两位同学在复习不等式过程中的对话:
小明说:”不等式a> 2a永远都不会成立,因为如果在这个不等式两边同时除以a,就.会出现1>2这样的错误结论!”
小丽说:“如果a>b,c>d,那么一定会得出a-c>b-d."
你认为小明的说法 (填“正确”或“不正确”);小丽的说法 (填“正确”或“不正确”),并选择其中一个人判断阐述你的理由(若认为正确,则进行证明;若认为不正确,则给出反例).
四、作图题
13.阅读下面材料:
判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
例如要判断命题“相等的角是对顶角”是假命题,可以举出如下反例:
如图,OC是∠AOB的平分线,∠1=∠2,但它们不是对顶角.
请你举出一个反例说明命题“如果两个角的两边分别平行,那么这两个角相等”是假命题.(要求:画出相应的图形,并用文字语言或符号语言表述所举反例)
五、综合题
14.用“如果……那么……”的形式改写下列命题。
(1)两条平行线被第三条直线所截,则它们的一对同位角的平分线互相平行。
(2)菱形的四边相等。
15.写出下列命题的条件和结论.
(1)如果a2=b2,那么a=b;
(2)同角或等角的补角相等;
(3)同旁内角互补,两直线平行.
16.如图,现有以下三个条件:①②③.请你以其中两个作为题设,另一个作为结论构造命题.
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).
17.判断下列命题是真命题还是假命题,如果是假命题,举出一个反例.
(1)等角的余角相等;
(2)平行线的同旁内角的平分线互相垂直;
(3)和为180°的两个角叫做邻补角.
答案解析部分
1.【答案】B
【知识点】真命题与假命题
2.【答案】C
【知识点】真命题与假命题
3.【答案】B
【知识点】真命题与假命题
4.【答案】D
【知识点】真命题与假命题
5.【答案】C
【知识点】平行线的性质;真命题与假命题
6.【答案】两个角是对顶角;这两个角相等
【知识点】定义、命题及定理的概念
7.【答案】如果两个角是同一个角的补角,那么这两个角相等
【知识点】定义、命题及定理的概念
8.【答案】一个三角形的两个角互余;这个三角形是直角三角形
【知识点】定义、命题及定理的概念
9.【答案】结论
【知识点】定义、命题及定理的概念
10.【答案】(1)解:条件是两直线平行;结论是同位角相等。
(2)解:条件是直线外有一点,过这一点做一条直线和已知直线平行;结论是这样的平行线有且只有一条。
【知识点】定义、命题及定理的概念
11.【答案】解:如果两个角是同一个角的补角,那么这两个角相等
【知识点】定义、命题及定理的概念
12.【答案】不正确;不正确
【知识点】真命题与假命题
13.【答案】解:如图,
∠1+∠2=180°;
如果两个角的两边分别平行,那么这两个角相等或互补.
【知识点】真命题与假命题
14.【答案】(1)解:如果两条平行线被第三条直线所截 那么它们的一对同位角的平分线互相平行
(2)解:如果一个四边形是菱形 那么四边相等。
【知识点】定义、命题及定理的概念
15.【答案】(1)解:条件:a2=b2;结论:a=b
(2)解:条件:两个角是同角或等角的补角;结论:这两个角相等
(3)解:条件:同旁内角互补;结论:两直线平行。
【知识点】定义、命题及定理的概念
16.【答案】(1)解:有:如果那么;
如果那么;
如果,那么;
(2)解:如图:
∵AB∥CD,
∴∠B=∠CDF,
∵∠B=∠C,
∴∠C=∠CDF,
∴CE∥BF,
∴∠E=∠F,
∴如果那么为真命题;
∵AB∥CD,
∴∠B=∠CDF,
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∴∠B=∠C,
∴如果那么为真命题;
∵∠E=∠F,
∴CE∥BF,
∴∠C=∠CDF,
∵∠B=∠C,
∴∠B=∠CDF,
∴AB∥CD,
∴如果,那么为真命题.
【知识点】定义、命题及定理的概念;真命题与假命题
17.【答案】(1)真命题;
(2)真命题;
(3)假命题,如两个不同书本上的两个和为180°的角.
【知识点】真命题与假命题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
