【浙教版八上同步练习】 1.3证明(含答案)
文档属性
| 名称 | 【浙教版八上同步练习】 1.3证明(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-26 14:02:31 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【浙教版八上同步练习】
1.3证明
一、单选题
1.下列说法中正确的是( )
A.两条相交的直线叫做平行线
B.在直线外一点,只能画出一条直线与已知直线平行
C.如果a∥b,b∥c,则a不与b平行
D.两条不平行的射线,在同一平面内一定相交
2.如图,已知 , , ,则 的度数为
A. B. C. D.
3.下列命题:①对顶角相等;②内错角相等;③平行于同一条直线的两条直线互相平行;④如果一个角的两边分别平行于另一个角的两边,那么这两个角相等.其中真命题是( )
A.①③ B.①④ C.①③④ D.①②③④
4.如图,已知AB⊥EF,CD⊥EF,直线AB、EF、GH相交于一点,若∠1=40°,则∠2等于( )
A.30° B.40° C.50° D.60°
5.两平行直线被第三条直线所截,同位角的平分线( )
A.互相重合 B.互相平行 C.互相垂直 D.相交
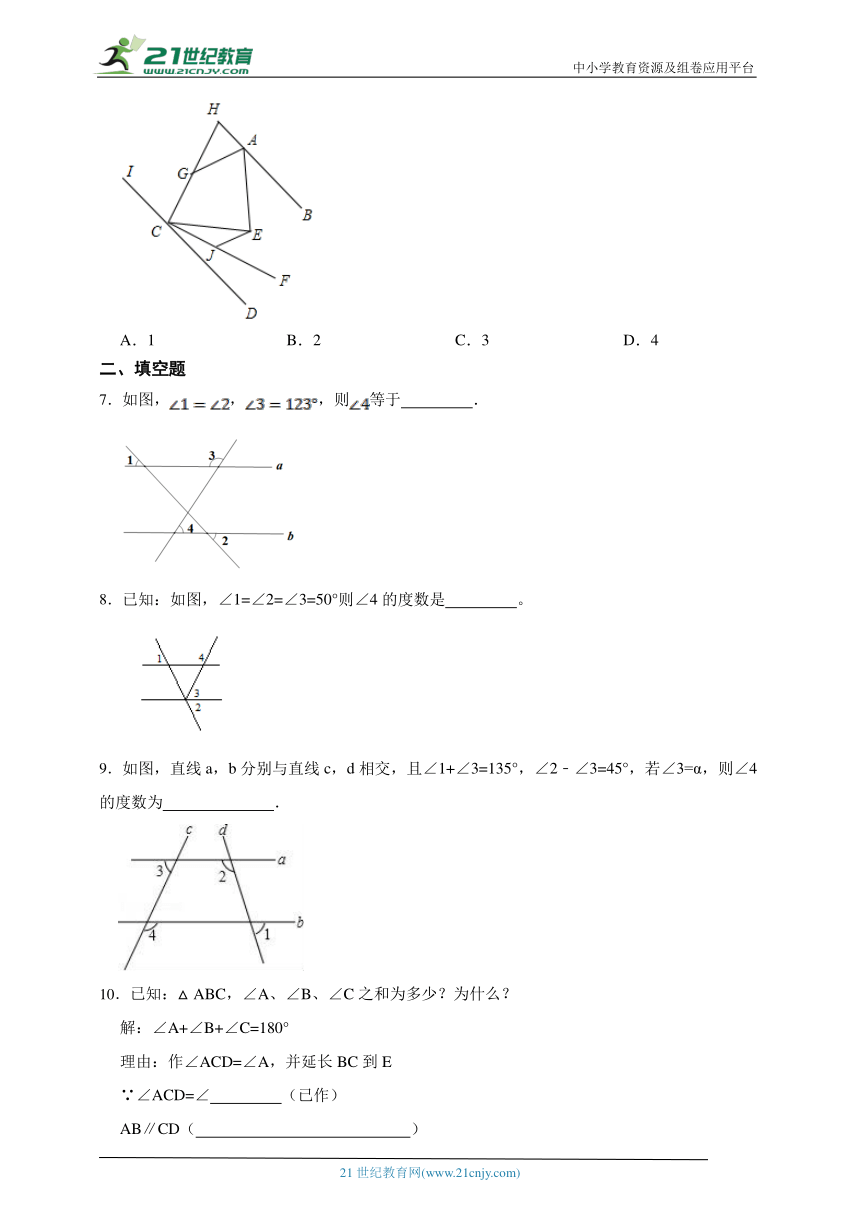
6.如图,AB∥CD,CF平分∠ECD,HC⊥CF交直线AB于H,AG平分∠HAE交HC于G,EJ∥AG交CF于J,∠AEC=80°,则下列结论正确的有( )个.
①∠BAE+∠ECD=80°;②CG平分∠ICE;③∠AGC=140°;④∠EJC﹣∠AGH=90°.
A.1 B.2 C.3 D.4
二、填空题
7.如图,,,则等于 .
8.已知:如图,∠1=∠2=∠3=50°则∠4的度数是 。
9.如图,直线a,b分别与直线c,d相交,且∠1+∠3=135°,∠2﹣∠3=45°,若∠3=α,则∠4的度数为 .
10.已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
解:∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延长BC到E
∵∠ACD=∠ (已作)
AB∥CD( )
∴∠B= ( )
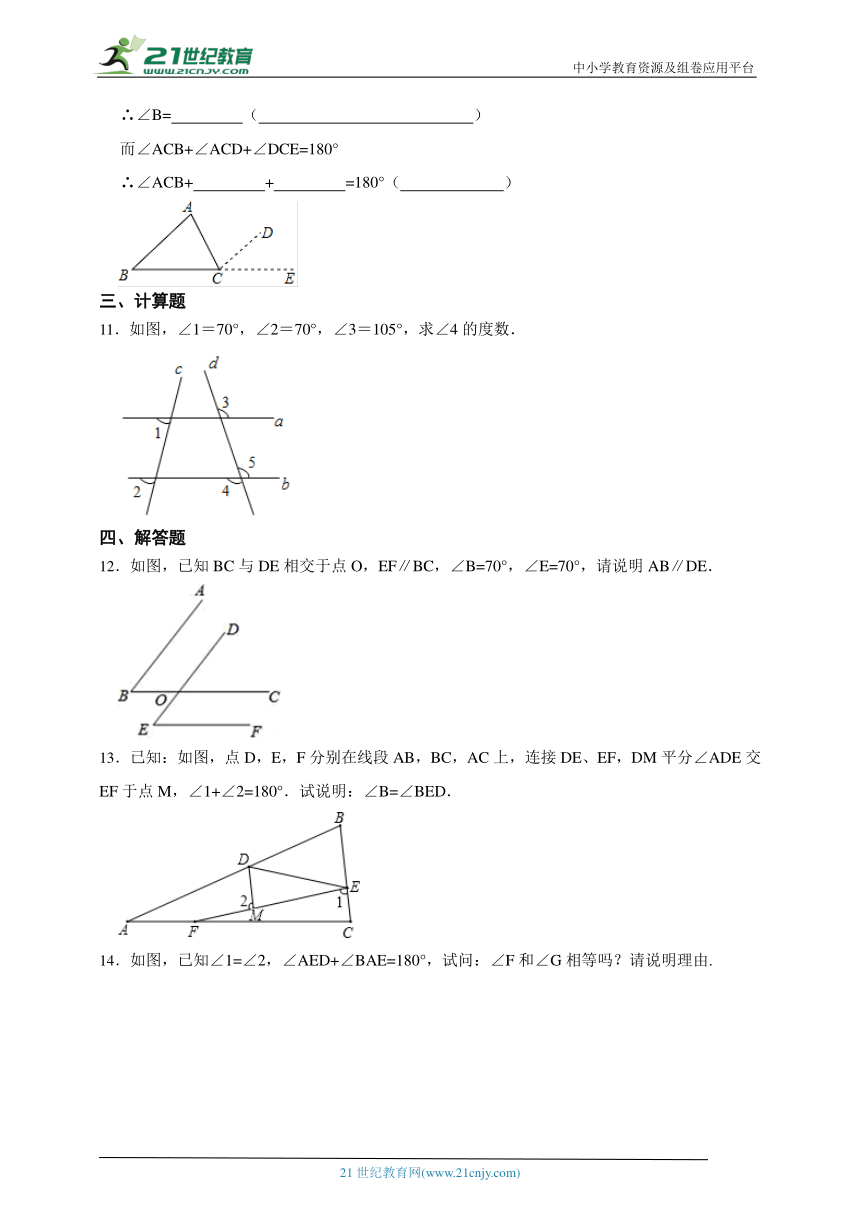
而∠ACB+∠ACD+∠DCE=180°
∴∠ACB+ + =180°( )
三、计算题
11.如图,∠1=70°,∠2=70°,∠3=105°,求∠4的度数.
四、解答题
12.如图,已知BC与DE相交于点O,EF∥BC,∠B=70°,∠E=70°,请说明AB∥DE.
13.已知:如图,点D,E,F分别在线段AB,BC,AC上,连接DE、EF,DM平分∠ADE交EF于点M,∠1+∠2=180°.试说明:∠B=∠BED.
14.如图,已知∠1=∠2,∠AED+∠BAE=180°,试问:∠F和∠G相等吗?请说明理由.
五、作图题
15.如图,线段 , 交于点 ,点 为线段 上一点(不与点 , 重合),且 为钝角过点 在 的右侧作射线 ,过点 作直线 ,交 于点 ( 与 不重合)
(1)按题目要求在图上补全图形;
(2)判断 与 的数量关系,并证明.
六、综合题
16.如图,直线分别交直线于点E,点F,,平分交于点G.
(1)求证:.
(2)若,求的度数.
17.如图,AB∥DG,∠1+∠2=180°,
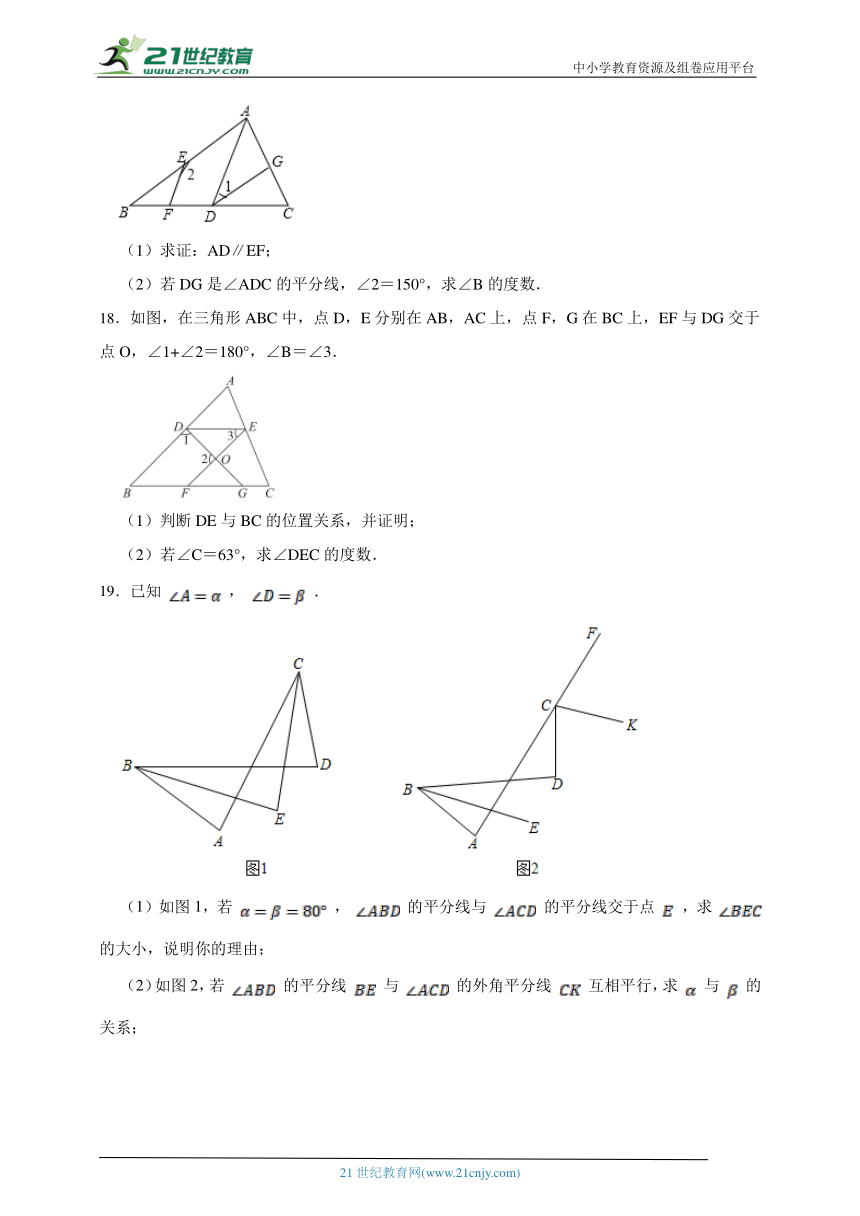
(1)求证:AD∥EF;
(2)若DG是∠ADC的平分线,∠2=150°,求∠B的度数.
18.如图,在三角形ABC中,点D,E分别在AB,AC上,点F,G在BC上,EF与DG交于点O,∠1+∠2=180°,∠B=∠3.
(1)判断DE与BC的位置关系,并证明;
(2)若∠C=63°,求∠DEC的度数.
19.已知 , .
(1)如图1,若 , 的平分线与 的平分线交于点 ,求 的大小,说明你的理由;
(2)如图2,若 的平分线 与 的外角平分线 互相平行,求 与 的关系;
答案解析部分
1.【答案】B
【知识点】平行线的判定与性质
2.【答案】D
【知识点】平行线的判定与性质
3.【答案】A
【知识点】平行线的判定与性质;真命题与假命题
4.【答案】B
【知识点】平行线的判定与性质
5.【答案】B
【知识点】平行线的判定与性质;角平分线的定义
6.【答案】D
【知识点】平行线的判定与性质;角平分线的定义
7.【答案】
【知识点】角的运算;平行线的判定与性质
8.【答案】130°
【知识点】平行线的判定与性质
9.【答案】180°﹣α
【知识点】平行线的判定与性质
10.【答案】A;内错角相等,两直线平行;∠DCE;两直线平行,同位角相等;∠A;∠B;等量代换
【知识点】平行线的判定与性质
11.【答案】解:∵∠1=70°,∠2=70°,
∴∠1=∠2,
∴a∥b,
∴∠3=∠5.
又∠3=105°,
∴∠5=105°,
∴∠4=∠5=105°.
【知识点】平行线的判定与性质
12.【答案】解:∵EF∥BC,∠E=70°,
∴∠DOC=∠E=70°,
∵∠B=70°,
∴∠DOC=∠B,
AB∥DE.
【知识点】平行线的判定与性质
13.【答案】证明:∵∠1+∠2=180°,∠1+∠BEF=180°,
∴∠2=∠BEF,
∴DM∥BE,
∴∠ADM=∠B,∠BED=∠EDM,
∵DM平分∠ADE,
∴∠ADM=∠EDM,
∴∠B=∠BED.
【知识点】等式的性质;余角、补角及其性质;平行线的判定与性质;角平分线的定义
14.【答案】解:相等.理由如下:
∵∠AED+∠BAE=180°,∴AB ∥CD,∴∠1+∠4=∠2+∠3.
又∵∠1=∠2,∴∠3=∠4,∴AG∥EF,∴∠F=∠G.
【知识点】平行线的判定与性质
15.【答案】(1)解:补全图如图:
(补全图基本正确即可给分);
(2)解:判断: ,
证明:过点 作 ,
(两直线平行,内错角相等).
∵ (已知),
(垂直的定义),
∴∠HCG=90°-∠1=90°-∠B,
∵ , ,
∴CH∥GF,
,
即 .
【知识点】垂线;平行线的判定与性质
16.【答案】(1)证明:∵ ,
∴ ,
∴ ;
(2)解:∵ ,
∴ ,
∵ 平分 ,
∴ ,
∵ ,
∴ .
【知识点】余角、补角及其性质;平行线的判定与性质;角平分线的定义
17.【答案】(1)证明:∵AB∥DG,
∴∠BAD=∠1,
∵∠1+∠2=180°,
∴∠2+∠BAD=180°,
∴AD∥EF
(2)解:∵∠1+∠2=180°,∠2=150°,
∴∠1=30°,
∵DG是∠ADC的平分线,
∴∠GDC=∠1=30°,
∵AB∥DG,
∴∠B=∠GDC=30°.
【知识点】平行线的判定与性质;角平分线的定义
18.【答案】(1)解:∵ ,
,
∴ ,
∵ ,
∴ ,
∴ ;
(2)∵ ,
∴ ,
又∵ ,
∴ .
【知识点】角的运算;平行线的判定与性质
19.【答案】(1)解:如图,在△ABG和△DCG中,
∠A=∠D=80°,∠AGB=∠CGD,
∴∠ABG=∠DCG,
又BE平分∠ABG,CE平分∠DCG,
∴∠ABF=∠GBF=∠DCE=∠GCE,
在△ABF和△ECF中,
∠ABF=∠ECF,∠AFB=∠EFC,
∴∠A=∠BEC=80°;
(2)解:如图,作∠ACD的平分线,交BE于P,
∵CK平分∠DCF,
∴∠PCK=∠PCD+∠KCD=90°,
∵CK∥BE,
∴∠BPC=∠PCK=90°,
在△ABG和△PCG中,
∠A+∠ABG=∠BPC+∠PCG,
即α+∠ABG=90°+∠PCG,①
在△PBH和△DCH中,
∠BPH+∠PBH=∠D+∠DCH,
即90°+∠PBH=β+∠DCH,②
∵BE平分∠ABD,CH平分∠ACD,
∴∠ABG=∠PBH,∠DCH=∠PCG,
∴①-②得:α-90°=90°-β,
化简得:α+β=180°.
【知识点】角的运算;平行线的判定与性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【浙教版八上同步练习】
1.3证明
一、单选题
1.下列说法中正确的是( )
A.两条相交的直线叫做平行线
B.在直线外一点,只能画出一条直线与已知直线平行
C.如果a∥b,b∥c,则a不与b平行
D.两条不平行的射线,在同一平面内一定相交
2.如图,已知 , , ,则 的度数为
A. B. C. D.
3.下列命题:①对顶角相等;②内错角相等;③平行于同一条直线的两条直线互相平行;④如果一个角的两边分别平行于另一个角的两边,那么这两个角相等.其中真命题是( )
A.①③ B.①④ C.①③④ D.①②③④
4.如图,已知AB⊥EF,CD⊥EF,直线AB、EF、GH相交于一点,若∠1=40°,则∠2等于( )
A.30° B.40° C.50° D.60°
5.两平行直线被第三条直线所截,同位角的平分线( )
A.互相重合 B.互相平行 C.互相垂直 D.相交
6.如图,AB∥CD,CF平分∠ECD,HC⊥CF交直线AB于H,AG平分∠HAE交HC于G,EJ∥AG交CF于J,∠AEC=80°,则下列结论正确的有( )个.
①∠BAE+∠ECD=80°;②CG平分∠ICE;③∠AGC=140°;④∠EJC﹣∠AGH=90°.
A.1 B.2 C.3 D.4
二、填空题
7.如图,,,则等于 .
8.已知:如图,∠1=∠2=∠3=50°则∠4的度数是 。
9.如图,直线a,b分别与直线c,d相交,且∠1+∠3=135°,∠2﹣∠3=45°,若∠3=α,则∠4的度数为 .
10.已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
解:∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延长BC到E
∵∠ACD=∠ (已作)
AB∥CD( )
∴∠B= ( )
而∠ACB+∠ACD+∠DCE=180°
∴∠ACB+ + =180°( )
三、计算题
11.如图,∠1=70°,∠2=70°,∠3=105°,求∠4的度数.
四、解答题
12.如图,已知BC与DE相交于点O,EF∥BC,∠B=70°,∠E=70°,请说明AB∥DE.
13.已知:如图,点D,E,F分别在线段AB,BC,AC上,连接DE、EF,DM平分∠ADE交EF于点M,∠1+∠2=180°.试说明:∠B=∠BED.
14.如图,已知∠1=∠2,∠AED+∠BAE=180°,试问:∠F和∠G相等吗?请说明理由.
五、作图题
15.如图,线段 , 交于点 ,点 为线段 上一点(不与点 , 重合),且 为钝角过点 在 的右侧作射线 ,过点 作直线 ,交 于点 ( 与 不重合)
(1)按题目要求在图上补全图形;
(2)判断 与 的数量关系,并证明.
六、综合题
16.如图,直线分别交直线于点E,点F,,平分交于点G.
(1)求证:.
(2)若,求的度数.
17.如图,AB∥DG,∠1+∠2=180°,
(1)求证:AD∥EF;
(2)若DG是∠ADC的平分线,∠2=150°,求∠B的度数.
18.如图,在三角形ABC中,点D,E分别在AB,AC上,点F,G在BC上,EF与DG交于点O,∠1+∠2=180°,∠B=∠3.
(1)判断DE与BC的位置关系,并证明;
(2)若∠C=63°,求∠DEC的度数.
19.已知 , .
(1)如图1,若 , 的平分线与 的平分线交于点 ,求 的大小,说明你的理由;
(2)如图2,若 的平分线 与 的外角平分线 互相平行,求 与 的关系;
答案解析部分
1.【答案】B
【知识点】平行线的判定与性质
2.【答案】D
【知识点】平行线的判定与性质
3.【答案】A
【知识点】平行线的判定与性质;真命题与假命题
4.【答案】B
【知识点】平行线的判定与性质
5.【答案】B
【知识点】平行线的判定与性质;角平分线的定义
6.【答案】D
【知识点】平行线的判定与性质;角平分线的定义
7.【答案】
【知识点】角的运算;平行线的判定与性质
8.【答案】130°
【知识点】平行线的判定与性质
9.【答案】180°﹣α
【知识点】平行线的判定与性质
10.【答案】A;内错角相等,两直线平行;∠DCE;两直线平行,同位角相等;∠A;∠B;等量代换
【知识点】平行线的判定与性质
11.【答案】解:∵∠1=70°,∠2=70°,
∴∠1=∠2,
∴a∥b,
∴∠3=∠5.
又∠3=105°,
∴∠5=105°,
∴∠4=∠5=105°.
【知识点】平行线的判定与性质
12.【答案】解:∵EF∥BC,∠E=70°,
∴∠DOC=∠E=70°,
∵∠B=70°,
∴∠DOC=∠B,
AB∥DE.
【知识点】平行线的判定与性质
13.【答案】证明:∵∠1+∠2=180°,∠1+∠BEF=180°,
∴∠2=∠BEF,
∴DM∥BE,
∴∠ADM=∠B,∠BED=∠EDM,
∵DM平分∠ADE,
∴∠ADM=∠EDM,
∴∠B=∠BED.
【知识点】等式的性质;余角、补角及其性质;平行线的判定与性质;角平分线的定义
14.【答案】解:相等.理由如下:
∵∠AED+∠BAE=180°,∴AB ∥CD,∴∠1+∠4=∠2+∠3.
又∵∠1=∠2,∴∠3=∠4,∴AG∥EF,∴∠F=∠G.
【知识点】平行线的判定与性质
15.【答案】(1)解:补全图如图:
(补全图基本正确即可给分);
(2)解:判断: ,
证明:过点 作 ,
(两直线平行,内错角相等).
∵ (已知),
(垂直的定义),
∴∠HCG=90°-∠1=90°-∠B,
∵ , ,
∴CH∥GF,
,
即 .
【知识点】垂线;平行线的判定与性质
16.【答案】(1)证明:∵ ,
∴ ,
∴ ;
(2)解:∵ ,
∴ ,
∵ 平分 ,
∴ ,
∵ ,
∴ .
【知识点】余角、补角及其性质;平行线的判定与性质;角平分线的定义
17.【答案】(1)证明:∵AB∥DG,
∴∠BAD=∠1,
∵∠1+∠2=180°,
∴∠2+∠BAD=180°,
∴AD∥EF
(2)解:∵∠1+∠2=180°,∠2=150°,
∴∠1=30°,
∵DG是∠ADC的平分线,
∴∠GDC=∠1=30°,
∵AB∥DG,
∴∠B=∠GDC=30°.
【知识点】平行线的判定与性质;角平分线的定义
18.【答案】(1)解:∵ ,
,
∴ ,
∵ ,
∴ ,
∴ ;
(2)∵ ,
∴ ,
又∵ ,
∴ .
【知识点】角的运算;平行线的判定与性质
19.【答案】(1)解:如图,在△ABG和△DCG中,
∠A=∠D=80°,∠AGB=∠CGD,
∴∠ABG=∠DCG,
又BE平分∠ABG,CE平分∠DCG,
∴∠ABF=∠GBF=∠DCE=∠GCE,
在△ABF和△ECF中,
∠ABF=∠ECF,∠AFB=∠EFC,
∴∠A=∠BEC=80°;
(2)解:如图,作∠ACD的平分线,交BE于P,
∵CK平分∠DCF,
∴∠PCK=∠PCD+∠KCD=90°,
∵CK∥BE,
∴∠BPC=∠PCK=90°,
在△ABG和△PCG中,
∠A+∠ABG=∠BPC+∠PCG,
即α+∠ABG=90°+∠PCG,①
在△PBH和△DCH中,
∠BPH+∠PBH=∠D+∠DCH,
即90°+∠PBH=β+∠DCH,②
∵BE平分∠ABD,CH平分∠ACD,
∴∠ABG=∠PBH,∠DCH=∠PCG,
∴①-②得:α-90°=90°-β,
化简得:α+β=180°.
【知识点】角的运算;平行线的判定与性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
