【浙教版八上同步练习】 1.4全等三角形(含答案)
文档属性
| 名称 | 【浙教版八上同步练习】 1.4全等三角形(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-26 14:07:27 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【浙教版八上同步练习】
1.4全等三角形
一、单选题
1.下列命题中正确的是( )
A.全等三角形的高相等
B.全等三角形的中线相等
C.全等三角形的垂直平分线相等
D.全等三角形对应角的平分线相等
2.如图, ,则 的长为( )
A. B. C. D.
3.△ABC≌△A′B′C′,其中∠A′=50°,∠B′=70°,则∠C的度数为( )
A.55° B.60° C.70° D.75°
4.如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( )
A.40° B.35° C.30° D.25°
5.如图,点,,在同一直线上,≌,,,则的长为( )
A. B. C. D.
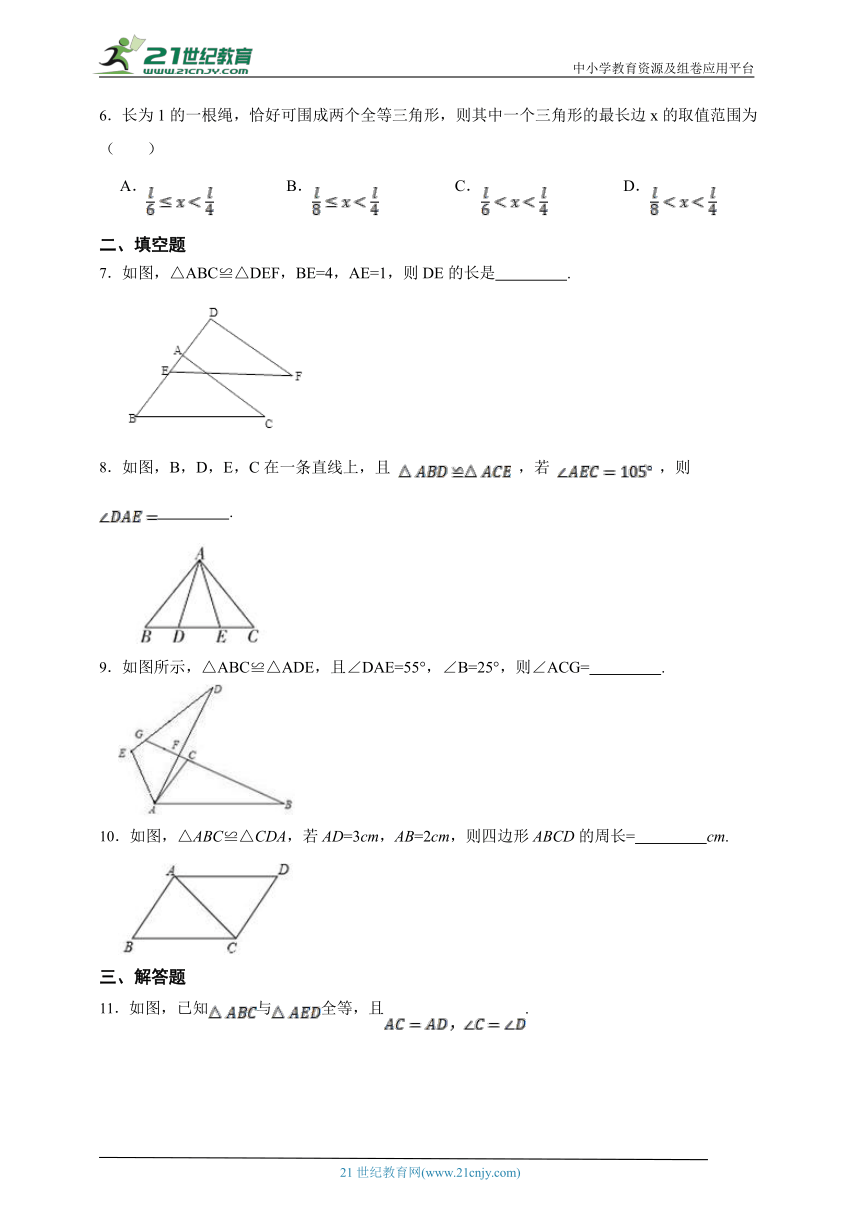
6.长为1的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为( )
A. B. C. D.
二、填空题
7.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是 .
8.如图,B,D,E,C在一条直线上,且 ,若 ,则 .
9.如图所示,△ABC≌△ADE,且∠DAE=55°,∠B=25°,则∠ACG= .
10.如图,△ABC≌△CDA,若AD=3cm,AB=2cm,则四边形ABCD的周长= cm.
三、解答题
11.如图,已知与全等,且.
(1)写出它们的对应边和对应角.
①对应边: .
②对应角: .
(2)由全等可推出 .理由:
,
,
即 .
12.如图,,在中,FG是最长的边,在中,MH是最长的边,和是对应角,且.
(1)写出对应相等的边及对应相等的角.
(2)求线段NM及线段HG的长度.
13.如图,点A,B,C,D在一条直线上,△ABF≌△DCE.你能得出哪些结论?(请写出三个以上的结论)
四、作图题
14.如图,是格点三角形顶点在网格线的交点上,请在下列每个方格纸上按要求画一个与全等的格点三角形,标注顶点字母并填空.
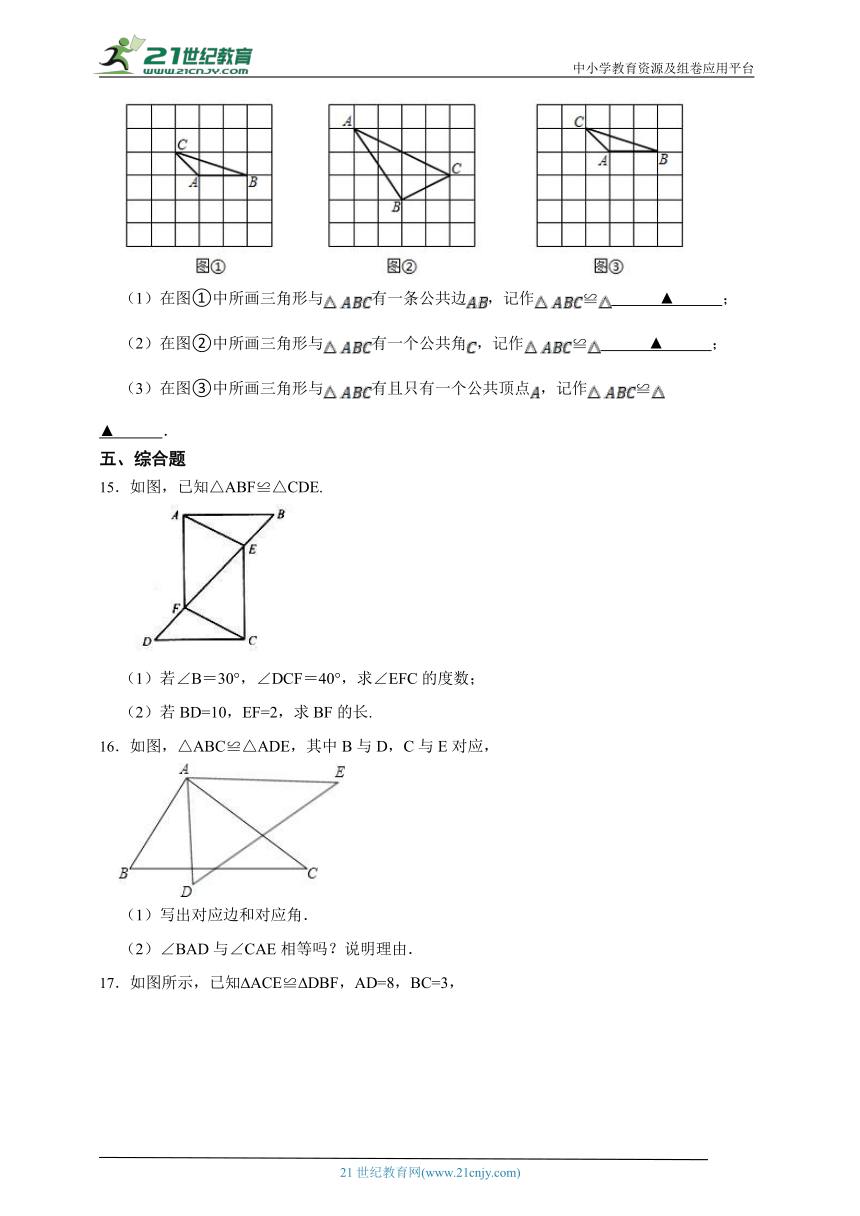
(1)在图①中所画三角形与有一条公共边,记作≌ ▲ ;
(2)在图②中所画三角形与有一个公共角,记作≌ ▲ ;
(3)在图③中所画三角形与有且只有一个公共顶点,记作≌ ▲ .
五、综合题
15.如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
16.如图,△ABC≌△ADE,其中B与D,C与E对应,
(1)写出对应边和对应角.
(2)∠BAD与∠CAE相等吗?说明理由.
17.如图所示,已知 ACE≌ DBF,AD=8,BC=3,
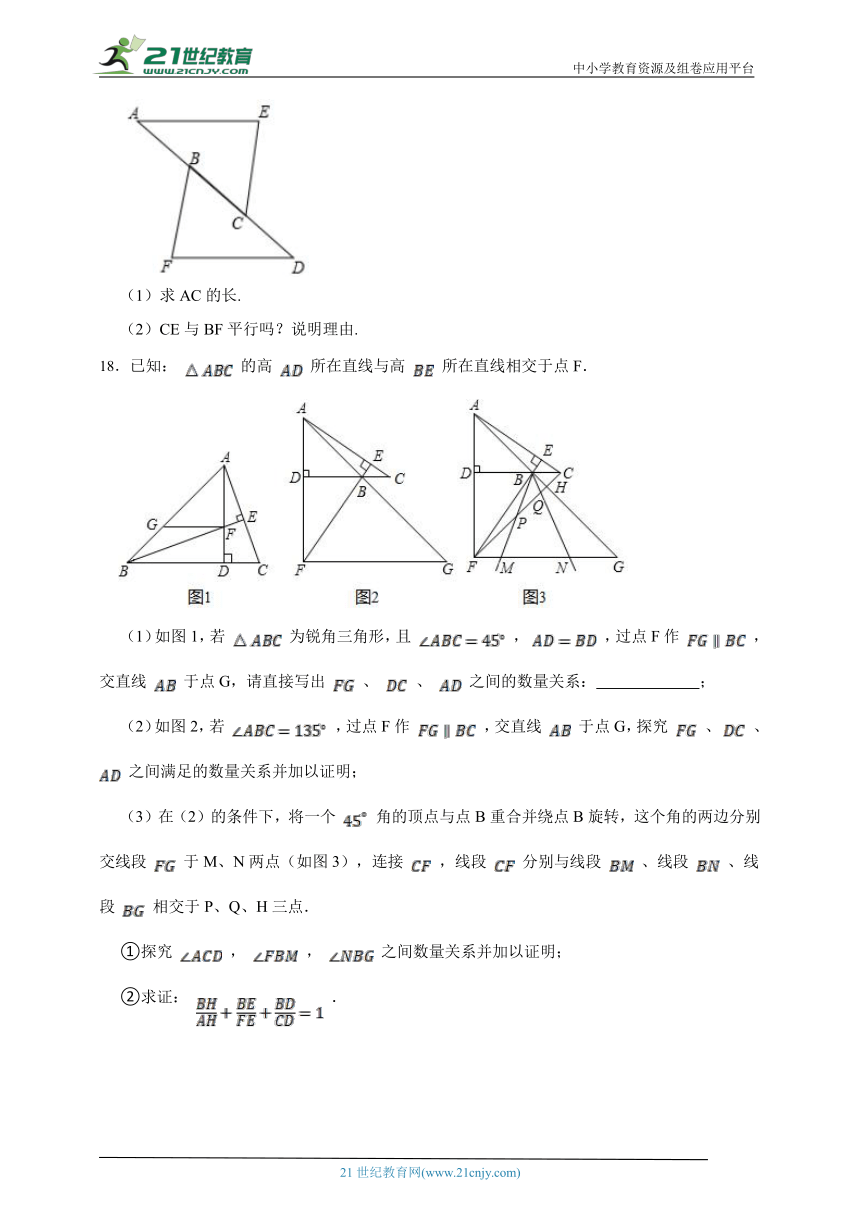
(1)求AC的长.
(2)CE与BF平行吗?说明理由.
18.已知: 的高 所在直线与高 所在直线相交于点F.
(1)如图1,若 为锐角三角形,且 , ,过点F作 ,交直线 于点G,请直接写出 、 、 之间的数量关系: ;
(2)如图2,若 ,过点F作 ,交直线 于点G,探究 、 、 之间满足的数量关系并加以证明;
(3)在(2)的条件下,将一个 角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段 于M、N两点(如图3),连接 ,线段 分别与线段 、线段 、线段 相交于P、Q、H三点.
①探究 , , 之间数量关系并加以证明;
②求证: .
答案解析部分
1.【答案】D
【知识点】三角形全等及其性质
2.【答案】C
【知识点】三角形全等及其性质
3.【答案】B
【知识点】三角形内角和定理;三角形全等及其性质
4.【答案】B
【知识点】三角形全等及其性质
5.【答案】B
【知识点】三角形全等及其性质
6.【答案】A
【知识点】三角形三边关系;三角形全等及其性质
7.【答案】5
【知识点】三角形全等及其性质
8.【答案】30°
【知识点】三角形内角和定理;三角形全等及其性质
9.【答案】80°
【知识点】三角形全等及其性质
10.【答案】10
【知识点】三角形全等及其性质
11.【答案】(1)AB和AE,AC和AD,BC和ED;∠BAC和和和
(2);;;
【知识点】三角形全等及其性质
12.【答案】(1)解:,
(2)解:∵△EFG≌△NMH,
【知识点】三角形全等及其性质
13.【答案】解:∵△ABF≌△DCE∴∠BAF=∠CDE,∠AFB=∠DEC,∠ABF=∠DCE,AB=DC,BF=CE,AF=DE;∴AF∥ED,AC=BD,BF∥CE
【知识点】平行线的判定;三角形全等及其性质
14.【答案】(1)解:如图①所示,即为所求
;ABD
(2)解:如图②所示,即为所求
;DEC
(3)解:如图③所示,即为所求,
;
DAE
【知识点】三角形全等及其性质
15.【答案】(1)解:∵△ABF≌△CDE,
∴∠B=∠D.
∵∠B=30°,
∴∠D=30°.
∵∠DCF=40°,
∴∠EFC=∠D+∠DCF=70°
(2)解:∵△ABF≌△CDE,
∴BF=DE
.∵BF=BE+EF,DE=DF+EF,
∴BE=DF.
∵BD=10,EF=2,
∴BE+DF=BD-EF=8,
∴BE=DF=4,
∴BF=BE+EF=6
【知识点】三角形全等及其性质
16.【答案】(1)解:对应边:AB与AD,BC与DE,AC与AE;
对应角:∠BAC与∠DAE,∠B与∠D,∠C与∠E;
(2)解:∠BAD=∠CAE.
理由如下:∵∠BAC=∠DAE,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE.
【知识点】三角形全等及其性质
17.【答案】(1)解: (已知),
(全等三角形的对应边相等),
即
(2)解:
理由如下:
(全等三角形的对应角相等),
(内错角相等,两直线平行)
【知识点】三角形全等及其性质
18.【答案】(1)
(2)解:结论:FG=DC+BD; 理由如下:
如图2
所示:
∠ADB=90°,
FG∥BD,
∴ ABD 和 AGF都是等腰直角三角形,
∴AD=BD,AF=FG,
∵AC⊥BF,
∴∠CEB=90°,
∴∠C+∠CBE=90°,
∵∠C+∠DAC=90°,∠CBE=∠DBF,
∴∠DAC=∠DBF,
∴ (ASA),
∴DC=DF,
∴AF=DF+AD=DC+AD,
∴FG=DC+AD.
(3)解:①解:结论:∠ACD=∠FBM+∠NBG.
理由:如图3中,
过点B作BT⊥FG于T.
∠BTG=90°,
∠G=45°,
∴∠TBG=45°,
∵∠MBN=45°,
∴∠MBT+∠NBT=∠NBT+∠GBN=45°,
∴∠MBT=∠GBN,
∴∠FBM+∠GBN=∠FBM+∠MBT=∠FBT,
∵BC∥FG,
∴∠FBD=∠BFT,
∵∠ECB+∠EBC=90°,∠BFT+∠FBT=90°,
∴∠ECB=∠FBT,
∴∠ACD=∠FBM+∠NBG.
②证明: 中,CD,FE是三角形的高,
∴AH⊥CF,
【知识点】三角形的面积;三角形全等及其性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【浙教版八上同步练习】
1.4全等三角形
一、单选题
1.下列命题中正确的是( )
A.全等三角形的高相等
B.全等三角形的中线相等
C.全等三角形的垂直平分线相等
D.全等三角形对应角的平分线相等
2.如图, ,则 的长为( )
A. B. C. D.
3.△ABC≌△A′B′C′,其中∠A′=50°,∠B′=70°,则∠C的度数为( )
A.55° B.60° C.70° D.75°
4.如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( )
A.40° B.35° C.30° D.25°
5.如图,点,,在同一直线上,≌,,,则的长为( )
A. B. C. D.
6.长为1的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为( )
A. B. C. D.
二、填空题
7.如图,△ABC≌△DEF,BE=4,AE=1,则DE的长是 .
8.如图,B,D,E,C在一条直线上,且 ,若 ,则 .
9.如图所示,△ABC≌△ADE,且∠DAE=55°,∠B=25°,则∠ACG= .
10.如图,△ABC≌△CDA,若AD=3cm,AB=2cm,则四边形ABCD的周长= cm.
三、解答题
11.如图,已知与全等,且.
(1)写出它们的对应边和对应角.
①对应边: .
②对应角: .
(2)由全等可推出 .理由:
,
,
即 .
12.如图,,在中,FG是最长的边,在中,MH是最长的边,和是对应角,且.
(1)写出对应相等的边及对应相等的角.
(2)求线段NM及线段HG的长度.
13.如图,点A,B,C,D在一条直线上,△ABF≌△DCE.你能得出哪些结论?(请写出三个以上的结论)
四、作图题
14.如图,是格点三角形顶点在网格线的交点上,请在下列每个方格纸上按要求画一个与全等的格点三角形,标注顶点字母并填空.
(1)在图①中所画三角形与有一条公共边,记作≌ ▲ ;
(2)在图②中所画三角形与有一个公共角,记作≌ ▲ ;
(3)在图③中所画三角形与有且只有一个公共顶点,记作≌ ▲ .
五、综合题
15.如图,已知△ABF≌△CDE.
(1)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(2)若BD=10,EF=2,求BF的长.
16.如图,△ABC≌△ADE,其中B与D,C与E对应,
(1)写出对应边和对应角.
(2)∠BAD与∠CAE相等吗?说明理由.
17.如图所示,已知 ACE≌ DBF,AD=8,BC=3,
(1)求AC的长.
(2)CE与BF平行吗?说明理由.
18.已知: 的高 所在直线与高 所在直线相交于点F.
(1)如图1,若 为锐角三角形,且 , ,过点F作 ,交直线 于点G,请直接写出 、 、 之间的数量关系: ;
(2)如图2,若 ,过点F作 ,交直线 于点G,探究 、 、 之间满足的数量关系并加以证明;
(3)在(2)的条件下,将一个 角的顶点与点B重合并绕点B旋转,这个角的两边分别交线段 于M、N两点(如图3),连接 ,线段 分别与线段 、线段 、线段 相交于P、Q、H三点.
①探究 , , 之间数量关系并加以证明;
②求证: .
答案解析部分
1.【答案】D
【知识点】三角形全等及其性质
2.【答案】C
【知识点】三角形全等及其性质
3.【答案】B
【知识点】三角形内角和定理;三角形全等及其性质
4.【答案】B
【知识点】三角形全等及其性质
5.【答案】B
【知识点】三角形全等及其性质
6.【答案】A
【知识点】三角形三边关系;三角形全等及其性质
7.【答案】5
【知识点】三角形全等及其性质
8.【答案】30°
【知识点】三角形内角和定理;三角形全等及其性质
9.【答案】80°
【知识点】三角形全等及其性质
10.【答案】10
【知识点】三角形全等及其性质
11.【答案】(1)AB和AE,AC和AD,BC和ED;∠BAC和和和
(2);;;
【知识点】三角形全等及其性质
12.【答案】(1)解:,
(2)解:∵△EFG≌△NMH,
【知识点】三角形全等及其性质
13.【答案】解:∵△ABF≌△DCE∴∠BAF=∠CDE,∠AFB=∠DEC,∠ABF=∠DCE,AB=DC,BF=CE,AF=DE;∴AF∥ED,AC=BD,BF∥CE
【知识点】平行线的判定;三角形全等及其性质
14.【答案】(1)解:如图①所示,即为所求
;ABD
(2)解:如图②所示,即为所求
;DEC
(3)解:如图③所示,即为所求,
;
DAE
【知识点】三角形全等及其性质
15.【答案】(1)解:∵△ABF≌△CDE,
∴∠B=∠D.
∵∠B=30°,
∴∠D=30°.
∵∠DCF=40°,
∴∠EFC=∠D+∠DCF=70°
(2)解:∵△ABF≌△CDE,
∴BF=DE
.∵BF=BE+EF,DE=DF+EF,
∴BE=DF.
∵BD=10,EF=2,
∴BE+DF=BD-EF=8,
∴BE=DF=4,
∴BF=BE+EF=6
【知识点】三角形全等及其性质
16.【答案】(1)解:对应边:AB与AD,BC与DE,AC与AE;
对应角:∠BAC与∠DAE,∠B与∠D,∠C与∠E;
(2)解:∠BAD=∠CAE.
理由如下:∵∠BAC=∠DAE,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE.
【知识点】三角形全等及其性质
17.【答案】(1)解: (已知),
(全等三角形的对应边相等),
即
(2)解:
理由如下:
(全等三角形的对应角相等),
(内错角相等,两直线平行)
【知识点】三角形全等及其性质
18.【答案】(1)
(2)解:结论:FG=DC+BD; 理由如下:
如图2
所示:
∠ADB=90°,
FG∥BD,
∴ ABD 和 AGF都是等腰直角三角形,
∴AD=BD,AF=FG,
∵AC⊥BF,
∴∠CEB=90°,
∴∠C+∠CBE=90°,
∵∠C+∠DAC=90°,∠CBE=∠DBF,
∴∠DAC=∠DBF,
∴ (ASA),
∴DC=DF,
∴AF=DF+AD=DC+AD,
∴FG=DC+AD.
(3)解:①解:结论:∠ACD=∠FBM+∠NBG.
理由:如图3中,
过点B作BT⊥FG于T.
∠BTG=90°,
∠G=45°,
∴∠TBG=45°,
∵∠MBN=45°,
∴∠MBT+∠NBT=∠NBT+∠GBN=45°,
∴∠MBT=∠GBN,
∴∠FBM+∠GBN=∠FBM+∠MBT=∠FBT,
∵BC∥FG,
∴∠FBD=∠BFT,
∵∠ECB+∠EBC=90°,∠BFT+∠FBT=90°,
∴∠ECB=∠FBT,
∴∠ACD=∠FBM+∠NBG.
②证明: 中,CD,FE是三角形的高,
∴AH⊥CF,
【知识点】三角形的面积;三角形全等及其性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
