【浙教版八上同步练习】 1.5三角形全等的判定(含答案)
文档属性
| 名称 | 【浙教版八上同步练习】 1.5三角形全等的判定(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-26 14:13:49 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【浙教版八上同步练习】
1.4三角形全等的判定
一、单选题
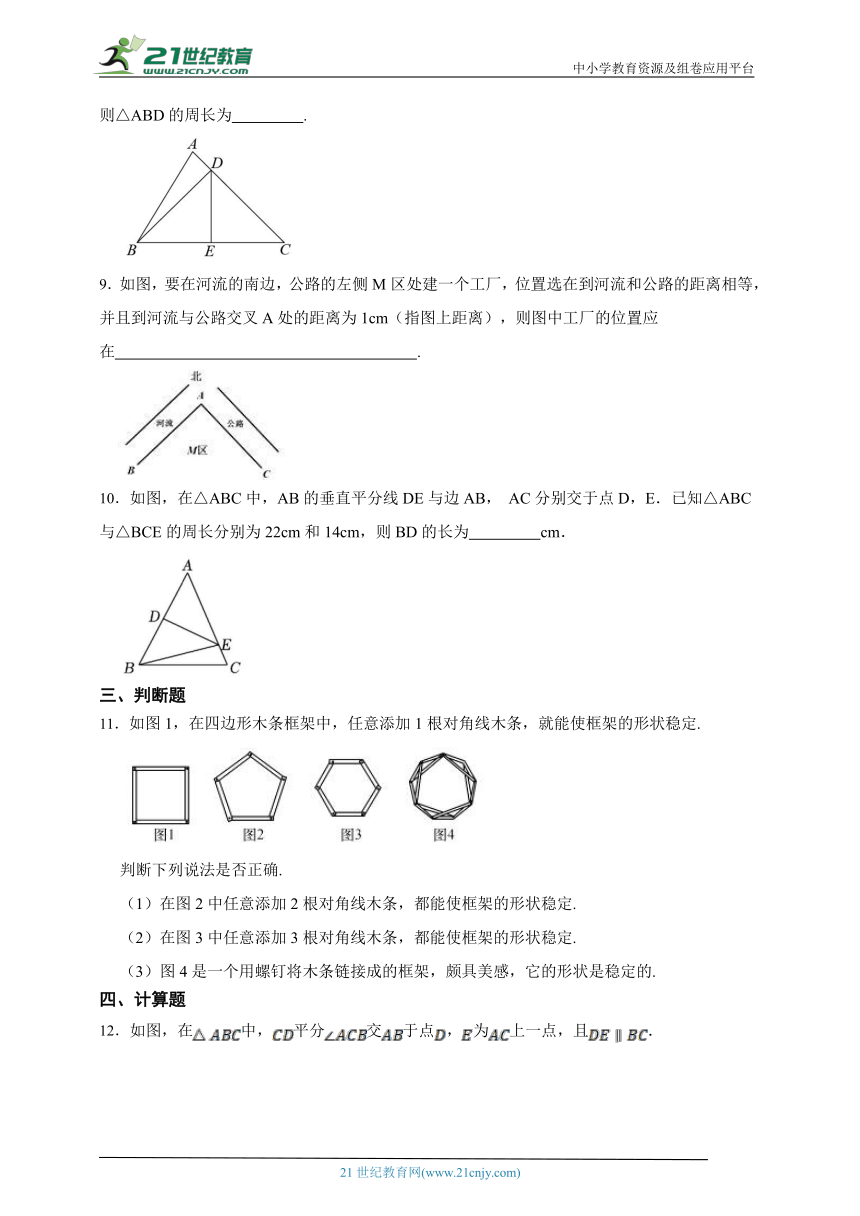
1.如图,△ABC中,AD平分∠BAC,AB=4,AC=2,若△ACD的面积等于3,则△ABD的面积为( )
A.8 B.4 C.6 D.12
2.如图, 、 分别为 、 边上的点, , .若 , ,则 的长度为( )
A.2 B.3 C.4 D.5
3.角平分线的尺规作图,其根据是构造两个全等三角形,由作图可知:判断所构造的两个三角形全等的依据是( )
A.SSS B.ASA C.SAS D.AAS
4.如图,公园里有一座假山,要测假山两端A,B的距离,先在平地上取一个可直接到达 A 和B的点C,分别延长AC,BC到D,E,使CD=CA ,CE=CB,连接DE.这样就可利用三角形全等,通过量出DE的长得到假山两端A,B的距离.其中说明两个三角形全等的依据是( )
A.SSS B.ASA C.AAS D.SAS
5.如图,在△ABC中,AB=AC,AB>BC,点D在BC边上,BD= DC,∠BED=∠CFD=∠BAC,若S△ABC=30,则阴影部分的面积为( )
A.5 B.10 C.15 D.20
6.如图,△ABC中,∠C=90°、AD是角平分线,E为AC边上的点,DE=DB,下列结论:①∠DEA+∠B=180°;② ∠CDE=∠CAB;③ AC= (AB+AE);④ S△ADC= S四边形ABDE,其中正确的结论个数为( )
A.4个 B.3个 C.2个 D.1个
二、填空题
7.如图,在△ABC和△DEF中,∠B=∠DEF,∠A=∠D,请你添加一个条件 ,使△ABC≌△DEF(图形中不再增加其他字母).
8.如图,在△ABC中,的垂直平分线交,于点,.若△ABC的周长为30,,则△ABD的周长为 .
9.如图,要在河流的南边,公路的左侧M区处建一个工厂,位置选在到河流和公路的距离相等,并且到河流与公路交叉A处的距离为1cm(指图上距离),则图中工厂的位置应在 .
10.如图,在△ABC中,AB的垂直平分线DE与边AB, AC分别交于点D,E.已知△ABC与△BCE的周长分别为22cm和14cm,则BD的长为 cm.
三、判断题
11.如图1,在四边形木条框架中,任意添加1根对角线木条,就能使框架的形状稳定.
判断下列说法是否正确.
(1)在图2中任意添加2根对角线木条,都能使框架的形状稳定.
(2)在图3中任意添加3根对角线木条,都能使框架的形状稳定.
(3)图4是一个用螺钉将木条链接成的框架,颇具美感,它的形状是稳定的.
四、计算题
12.如图,在中,平分交于点,为上一点,且.
(1)求证:;
(2)若,,,求的面积.
五、解答题
13.已知:如图,点E,F是BD上的点,∠AED=∠CFB,AE=CF,BE=DF.
求证:AB∥CD,AB=CD.
14.如图,已知点B,C,F,E在同一直线上,∠1=∠2,BF=CE,AB∥DE.
求证:△ABC≌△DEF.
15.如图,△ABC与△ABD中,AD与BC相交于O点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC=BD,并给出证明.
你添加的条件是?并证明。
六、作图题
16.根据图中尺规作图的痕迹,先判断得出结论: ,然后证明你的结论(不要求写已知、求证)
七、综合题
17.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE,垂足E,AD⊥CE, 垂足为 D,AD=2.5cm,BE=1.7cm,
(1)求证:△BCE≌△CAD
(2)求DE 的长.
18.如图,AB∥CD,AB=CD,点E,F在BC上,且BE=CF.
求证:
(1)AF=DE;
(2)AF∥DE.
19.如图:AB=AC,AD=AE,AB⊥AC,AD⊥AE。
(1)求证:△EAC≌△DAB
(2)判断线段EC与线段BD的关系,并说明理由
20.初步探索:如图:在四边形中,,,、分别是、上的点,且,探究图中、、之间的数量关系.
(1)小明同学探究此问题的方法是:延长到点,使.连接,先证明,再证明,可得出结论,他的结论应是 ;
(2)如图2,若在四边形中,,,、分别是、上的点,且,上述结论是否仍然成立,并说明理由;
答案解析部分
1.【答案】C
【知识点】三角形的面积;角平分线的性质
2.【答案】B
【知识点】三角形全等的判定(AAS)
3.【答案】A
【知识点】三角形全等的判定(SSS)
4.【答案】D
【知识点】三角形全等的判定(SAS)
5.【答案】D
【知识点】三角形的面积;三角形全等的判定(ASA)
6.【答案】A
【知识点】三角形全等及其性质;角平分线的性质;角平分线的定义
7.【答案】AB=ED
【知识点】三角形全等的判定
8.【答案】20
【知识点】线段垂直平分线的性质
9.【答案】∠BAC的平分线上,与A相距1cm的地方
【知识点】角平分线的性质
10.【答案】4
【知识点】线段垂直平分线的性质
11.【答案】(1)正确
(2)错误
(3)正确
【知识点】三角形的稳定性
12.【答案】(1)证明:
∵CD平分∠ACB,∴∠1=∠2,
∵DE∥BC,∴∠3=∠1=∠2,∴DE=CE.
(2)解:作DF⊥BC交BC于F,
∵CD平分∠ACB,∠A=∠DFC=90°,∴AD=DF=4,
∴.
【知识点】平行线的性质;三角形的面积;角平分线的性质;角平分线的定义
13.【答案】证明:∵∠AED=∠CFB,
∴∠AEB=∠CFD,
∵AE=CF,BE=DF,
∴△ABE≌△CDF(SAS),
∴AB=CD,∠ABD=∠CDB,
∴AB∥CD.
【知识点】平行线的判定;三角形全等的判定(SAS)
14.【答案】解:∵BF=CE,
∴BF-FC=CE-CF,即BC=EF,
∵AB∥DE,
∴∠E=∠B,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS).
【知识点】三角形全等的判定
15.【答案】解:添加条件例举:AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC等.
证明:①如果添加条件是AD=BC时,
∵BC=AD,∠2=∠1,AB=BA,
在△ABC与△BAD中,
,
∴△ABC≌△BAD,
∴AC=BD;
②如果添加条件是OC=OD时,
∵∠1=∠2
∴OA=OB
∴OA+OD=OB+OD
∴BC=AD
又∵∠2=∠1,AB=BA
在△ABC与△BAD中, ,
∴△ABC≌△BAD,
∴AC=BD;
③如果添加条件是∠C=∠D时,
∵∠2=∠1,AB=BA,
在△ABC与△BAD中,
,
∴△ABC≌△BAD,
∴AC=BD;
④如果添加条件是∠CAO=∠DBC时,
∵∠1=∠2,
∴∠CAO+∠1=∠DBC+∠2,
∴∠CAB=∠DBA,
又∵AB=BA,∠2=∠1,
在△ABC与△BAD中, ,
∴△ABC≌△BAD,
∴AC=BD.
故答案为:AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC.
【知识点】全等三角形的判定与性质
16.【答案】【解答】解:结论:OM平分∠BOA,
证明:由作图的痕迹可知,OC=OD,CM=DM,
在△COM和△DOM中,
,
∴△COM≌△DOM,
∴∠COM=∠DOM,
∴OM平分∠BOA.
【知识点】三角形全等的判定(SSS);作图-角的平分线
17.【答案】(1)证明:∵AD⊥CE,BE⊥CE,
∴∠E=∠ADC=90°,
即 ∠CAD+∠ACD=90°,∵∠ACB=90°,
∴∠BCE+∠ACD=90°
∴∠BCE=∠CAD,
在△BCE和△CAD中,
∴△BCE≌△CAD(AAS)
(2)解:∵△BCE≌△CAD ,
∴CE=AD, BE=CD,
∴DE=CE-CD=2.5-1.7=0.8cm
【知识点】三角形全等的判定
18.【答案】(1)证明:如图,AB∥CD,
∴∠B=∠C.
∵BE=CF,
∴BE-EF=CF-EF,
即BF=CE,
在△ABF和△DCE中
AB=DC
∠B=∠C
BF=CE
∴△ABF≌△DCE(SAS)
∴AF=DE
(2)证明:∵△ABF≌△DCE
∴ ∠AFB=∠DEC,
∴∠AFE=∠DEF,
∴AF∥DE.
【知识点】三角形全等及其性质;三角形全等的判定
19.【答案】(1)解: ∵AB⊥AC,AD⊥AE,
∴∠EAD=∠BAC=90°,
∴∴∠EAD+∠DAC=∠BAC+∠DAC即∠EAC=∠DAB,
在△EAC和△DAB中,
∴ △EAC≌△DAB(SAS)
(2)解: 线段EC与线段BD的关系为:相等且互相垂直.
理由:如图,
∵△EAC≌△DAB
∴∠E=∠D,EC=BD
∵∠EAD=90°,
∴∠E+∠EFA=90°,
∵∠EFA=∠DFG,
∴∠D+∠DFG=90°,
∴∠DGF=90°,
∴EC⊥BD
∴线段EC与线段BD的关系为:相等且互相垂直
【知识点】垂线;全等三角形的判定与性质
20.【答案】(1)∠BAE+∠FAD=∠EAF
(2)解:如图2,延长FD到点G,使DG=BE,连接AG,
∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,
∴∠B=∠ADG,
又∵AB=AD,
∴△ABE≌△ADG(SAS),
∴∠BAE=∠DAG,AE=AG,
∵EF=BE+FD=DG+FD=GF,AF=AF,
∴△AEF≌△AGF(SSS),
∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF
【知识点】余角、补角及其性质;三角形全等的判定(SSS);三角形全等的判定(SAS)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【浙教版八上同步练习】
1.4三角形全等的判定
一、单选题
1.如图,△ABC中,AD平分∠BAC,AB=4,AC=2,若△ACD的面积等于3,则△ABD的面积为( )
A.8 B.4 C.6 D.12
2.如图, 、 分别为 、 边上的点, , .若 , ,则 的长度为( )
A.2 B.3 C.4 D.5
3.角平分线的尺规作图,其根据是构造两个全等三角形,由作图可知:判断所构造的两个三角形全等的依据是( )
A.SSS B.ASA C.SAS D.AAS
4.如图,公园里有一座假山,要测假山两端A,B的距离,先在平地上取一个可直接到达 A 和B的点C,分别延长AC,BC到D,E,使CD=CA ,CE=CB,连接DE.这样就可利用三角形全等,通过量出DE的长得到假山两端A,B的距离.其中说明两个三角形全等的依据是( )
A.SSS B.ASA C.AAS D.SAS
5.如图,在△ABC中,AB=AC,AB>BC,点D在BC边上,BD= DC,∠BED=∠CFD=∠BAC,若S△ABC=30,则阴影部分的面积为( )
A.5 B.10 C.15 D.20
6.如图,△ABC中,∠C=90°、AD是角平分线,E为AC边上的点,DE=DB,下列结论:①∠DEA+∠B=180°;② ∠CDE=∠CAB;③ AC= (AB+AE);④ S△ADC= S四边形ABDE,其中正确的结论个数为( )
A.4个 B.3个 C.2个 D.1个
二、填空题
7.如图,在△ABC和△DEF中,∠B=∠DEF,∠A=∠D,请你添加一个条件 ,使△ABC≌△DEF(图形中不再增加其他字母).
8.如图,在△ABC中,的垂直平分线交,于点,.若△ABC的周长为30,,则△ABD的周长为 .
9.如图,要在河流的南边,公路的左侧M区处建一个工厂,位置选在到河流和公路的距离相等,并且到河流与公路交叉A处的距离为1cm(指图上距离),则图中工厂的位置应在 .
10.如图,在△ABC中,AB的垂直平分线DE与边AB, AC分别交于点D,E.已知△ABC与△BCE的周长分别为22cm和14cm,则BD的长为 cm.
三、判断题
11.如图1,在四边形木条框架中,任意添加1根对角线木条,就能使框架的形状稳定.
判断下列说法是否正确.
(1)在图2中任意添加2根对角线木条,都能使框架的形状稳定.
(2)在图3中任意添加3根对角线木条,都能使框架的形状稳定.
(3)图4是一个用螺钉将木条链接成的框架,颇具美感,它的形状是稳定的.
四、计算题
12.如图,在中,平分交于点,为上一点,且.
(1)求证:;
(2)若,,,求的面积.
五、解答题
13.已知:如图,点E,F是BD上的点,∠AED=∠CFB,AE=CF,BE=DF.
求证:AB∥CD,AB=CD.
14.如图,已知点B,C,F,E在同一直线上,∠1=∠2,BF=CE,AB∥DE.
求证:△ABC≌△DEF.
15.如图,△ABC与△ABD中,AD与BC相交于O点,∠1=∠2,请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使AC=BD,并给出证明.
你添加的条件是?并证明。
六、作图题
16.根据图中尺规作图的痕迹,先判断得出结论: ,然后证明你的结论(不要求写已知、求证)
七、综合题
17.如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE,垂足E,AD⊥CE, 垂足为 D,AD=2.5cm,BE=1.7cm,
(1)求证:△BCE≌△CAD
(2)求DE 的长.
18.如图,AB∥CD,AB=CD,点E,F在BC上,且BE=CF.
求证:
(1)AF=DE;
(2)AF∥DE.
19.如图:AB=AC,AD=AE,AB⊥AC,AD⊥AE。
(1)求证:△EAC≌△DAB
(2)判断线段EC与线段BD的关系,并说明理由
20.初步探索:如图:在四边形中,,,、分别是、上的点,且,探究图中、、之间的数量关系.
(1)小明同学探究此问题的方法是:延长到点,使.连接,先证明,再证明,可得出结论,他的结论应是 ;
(2)如图2,若在四边形中,,,、分别是、上的点,且,上述结论是否仍然成立,并说明理由;
答案解析部分
1.【答案】C
【知识点】三角形的面积;角平分线的性质
2.【答案】B
【知识点】三角形全等的判定(AAS)
3.【答案】A
【知识点】三角形全等的判定(SSS)
4.【答案】D
【知识点】三角形全等的判定(SAS)
5.【答案】D
【知识点】三角形的面积;三角形全等的判定(ASA)
6.【答案】A
【知识点】三角形全等及其性质;角平分线的性质;角平分线的定义
7.【答案】AB=ED
【知识点】三角形全等的判定
8.【答案】20
【知识点】线段垂直平分线的性质
9.【答案】∠BAC的平分线上,与A相距1cm的地方
【知识点】角平分线的性质
10.【答案】4
【知识点】线段垂直平分线的性质
11.【答案】(1)正确
(2)错误
(3)正确
【知识点】三角形的稳定性
12.【答案】(1)证明:
∵CD平分∠ACB,∴∠1=∠2,
∵DE∥BC,∴∠3=∠1=∠2,∴DE=CE.
(2)解:作DF⊥BC交BC于F,
∵CD平分∠ACB,∠A=∠DFC=90°,∴AD=DF=4,
∴.
【知识点】平行线的性质;三角形的面积;角平分线的性质;角平分线的定义
13.【答案】证明:∵∠AED=∠CFB,
∴∠AEB=∠CFD,
∵AE=CF,BE=DF,
∴△ABE≌△CDF(SAS),
∴AB=CD,∠ABD=∠CDB,
∴AB∥CD.
【知识点】平行线的判定;三角形全等的判定(SAS)
14.【答案】解:∵BF=CE,
∴BF-FC=CE-CF,即BC=EF,
∵AB∥DE,
∴∠E=∠B,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS).
【知识点】三角形全等的判定
15.【答案】解:添加条件例举:AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC等.
证明:①如果添加条件是AD=BC时,
∵BC=AD,∠2=∠1,AB=BA,
在△ABC与△BAD中,
,
∴△ABC≌△BAD,
∴AC=BD;
②如果添加条件是OC=OD时,
∵∠1=∠2
∴OA=OB
∴OA+OD=OB+OD
∴BC=AD
又∵∠2=∠1,AB=BA
在△ABC与△BAD中, ,
∴△ABC≌△BAD,
∴AC=BD;
③如果添加条件是∠C=∠D时,
∵∠2=∠1,AB=BA,
在△ABC与△BAD中,
,
∴△ABC≌△BAD,
∴AC=BD;
④如果添加条件是∠CAO=∠DBC时,
∵∠1=∠2,
∴∠CAO+∠1=∠DBC+∠2,
∴∠CAB=∠DBA,
又∵AB=BA,∠2=∠1,
在△ABC与△BAD中, ,
∴△ABC≌△BAD,
∴AC=BD.
故答案为:AD=BC;OC=OD;∠C=∠D;∠CAO=∠DBC.
【知识点】全等三角形的判定与性质
16.【答案】【解答】解:结论:OM平分∠BOA,
证明:由作图的痕迹可知,OC=OD,CM=DM,
在△COM和△DOM中,
,
∴△COM≌△DOM,
∴∠COM=∠DOM,
∴OM平分∠BOA.
【知识点】三角形全等的判定(SSS);作图-角的平分线
17.【答案】(1)证明:∵AD⊥CE,BE⊥CE,
∴∠E=∠ADC=90°,
即 ∠CAD+∠ACD=90°,∵∠ACB=90°,
∴∠BCE+∠ACD=90°
∴∠BCE=∠CAD,
在△BCE和△CAD中,
∴△BCE≌△CAD(AAS)
(2)解:∵△BCE≌△CAD ,
∴CE=AD, BE=CD,
∴DE=CE-CD=2.5-1.7=0.8cm
【知识点】三角形全等的判定
18.【答案】(1)证明:如图,AB∥CD,
∴∠B=∠C.
∵BE=CF,
∴BE-EF=CF-EF,
即BF=CE,
在△ABF和△DCE中
AB=DC
∠B=∠C
BF=CE
∴△ABF≌△DCE(SAS)
∴AF=DE
(2)证明:∵△ABF≌△DCE
∴ ∠AFB=∠DEC,
∴∠AFE=∠DEF,
∴AF∥DE.
【知识点】三角形全等及其性质;三角形全等的判定
19.【答案】(1)解: ∵AB⊥AC,AD⊥AE,
∴∠EAD=∠BAC=90°,
∴∴∠EAD+∠DAC=∠BAC+∠DAC即∠EAC=∠DAB,
在△EAC和△DAB中,
∴ △EAC≌△DAB(SAS)
(2)解: 线段EC与线段BD的关系为:相等且互相垂直.
理由:如图,
∵△EAC≌△DAB
∴∠E=∠D,EC=BD
∵∠EAD=90°,
∴∠E+∠EFA=90°,
∵∠EFA=∠DFG,
∴∠D+∠DFG=90°,
∴∠DGF=90°,
∴EC⊥BD
∴线段EC与线段BD的关系为:相等且互相垂直
【知识点】垂线;全等三角形的判定与性质
20.【答案】(1)∠BAE+∠FAD=∠EAF
(2)解:如图2,延长FD到点G,使DG=BE,连接AG,
∵∠B+∠ADF=180°,∠ADG+∠ADF=180°,
∴∠B=∠ADG,
又∵AB=AD,
∴△ABE≌△ADG(SAS),
∴∠BAE=∠DAG,AE=AG,
∵EF=BE+FD=DG+FD=GF,AF=AF,
∴△AEF≌△AGF(SSS),
∴∠EAF=∠GAF=∠DAG+∠DAF=∠BAE+∠DAF
【知识点】余角、补角及其性质;三角形全等的判定(SSS);三角形全等的判定(SAS)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
