【浙教版八上同步练习】 2.1图形的轴对称(含答案)
文档属性
| 名称 | 【浙教版八上同步练习】 2.1图形的轴对称(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-26 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【浙教版八上同步练习】
2.1图形的轴对称
一、单选题
1.在一些汉字的美术字中,有的是轴对称图形.下面五个词中“自由 平等 民主 敬业 友善”可以看作轴对称图形的汉字有 个.( )
A.2个 B.3个 C.4个 D.5个
2.一个企业的logo(标志)代表着一种精神,一种企业文化,以下是深圳市四个公司的logo,其中是轴对称图形的是( )
A. B.
C. D.
3.下列“QQ表情”中,属于轴对称图形的是 ( )
A. B. C. D.
4.人有忧喜,岁分四季,而在四季里,又分风、云、雨、雪、霜、露、虹、雾、雷等多种天气,可谓是气象万千,变幻莫测,下面是常用的天气符号,图片上有图案和文字说明,其中的图案不是轴对称图形的是( )
A.霜冻 B.雷雨
C.雾 D.小雪
5.如图,对角线AC将正方形ABCD分成两个等腰三角形,点E,F将对角线AC三等分,且AC=15,点P在正方形的边上,则满足PE+PF=5 的点P的个数是( )
A.0 B.4 C.8 D.16
二、填空题
6.如图, , , 与 关于直线l对称,则∠B= .
7.如图,△ABC与△A′B′C′关于直线 对称,则∠B的度数为 °
8.如图,已知点 .规定“把点 先作关于 轴对称,再向左平移1个单位”为一次变换.经过第一次变换后,点 的坐标为 ;经过第二次变换后,点 的坐标为 ;那么连续经过2019次变换后,点 的坐标为 .
9.如图,在△ABC中,∠BCA=120°,∠A=15°,AC=5,点M、N分别是AB、AC上动点,则CM+MN的最小值为 .
10.如图,正方形ABCD中,AB=2,连接AC,∠ACD的平分线交AD于点E,在AB上截取AF=DE,连接DF,分别交CE,AC于点G,H,点P是线段GC上的动点,PQ⊥AC于点Q,连接PH,则PH+PQ的最小值是 .
三、解答题
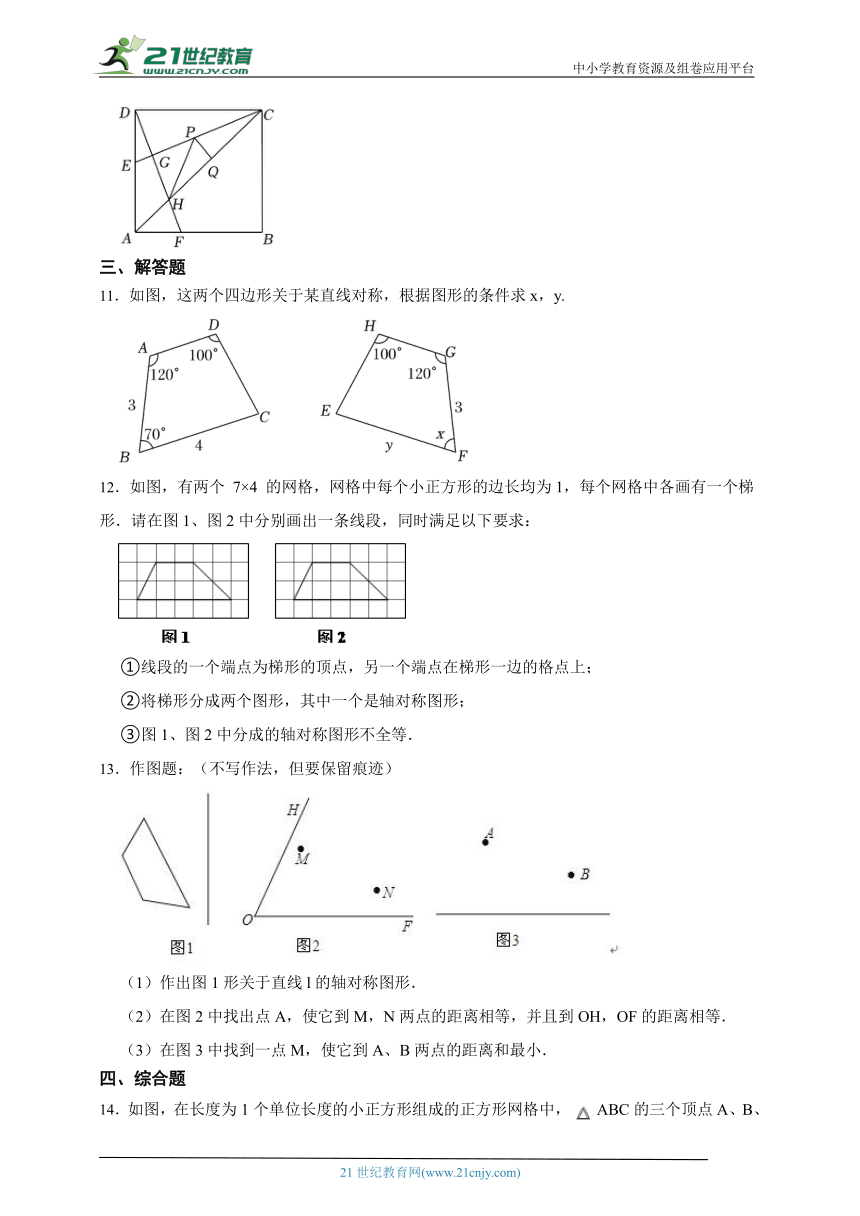
11.如图,这两个四边形关于某直线对称,根据图形的条件求x,y.
12.如图,有两个 7×4 的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
①线段的一个端点为梯形的顶点,另一个端点在梯形一边的格点上;
②将梯形分成两个图形,其中一个是轴对称图形;
③图1、图2中分成的轴对称图形不全等.
13.作图题:(不写作法,但要保留痕迹)
(1)作出图1形关于直线l的轴对称图形.
(2)在图2中找出点A,使它到M,N两点的距离相等,并且到OH,OF的距离相等.
(3)在图3中找到一点M,使它到A、B两点的距离和最小.
四、综合题
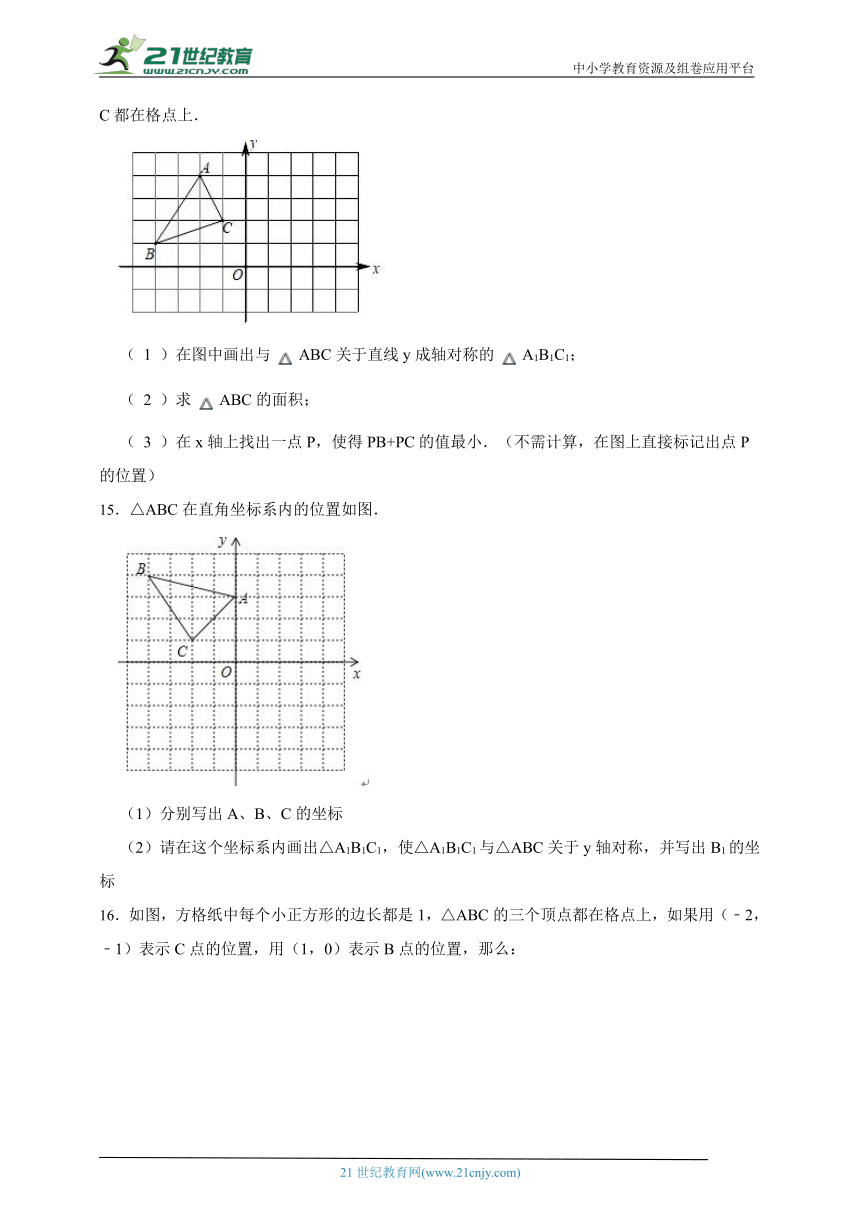
14.如图,在长度为1个单位长度的小正方形组成的正方形网格中, ABC的三个顶点A、B、C都在格点上.
( 1 )在图中画出与 ABC关于直线y成轴对称的 A1B1C1;
( 2 )求 ABC的面积;
( 3 )在x轴上找出一点P,使得PB+PC的值最小.(不需计算,在图上直接标记出点P的位置)
15.△ABC在直角坐标系内的位置如图.
(1)分别写出A、B、C的坐标
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标
16.如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(﹣2,﹣1)表示C点的位置,用(1,0)表示B点的位置,那么:
(1)画出直角坐标系.
(2)画出与△ABC关于y轴对称的图形△DEF.
(3)分别写出点D、E、F的坐标.
五、实践探究题
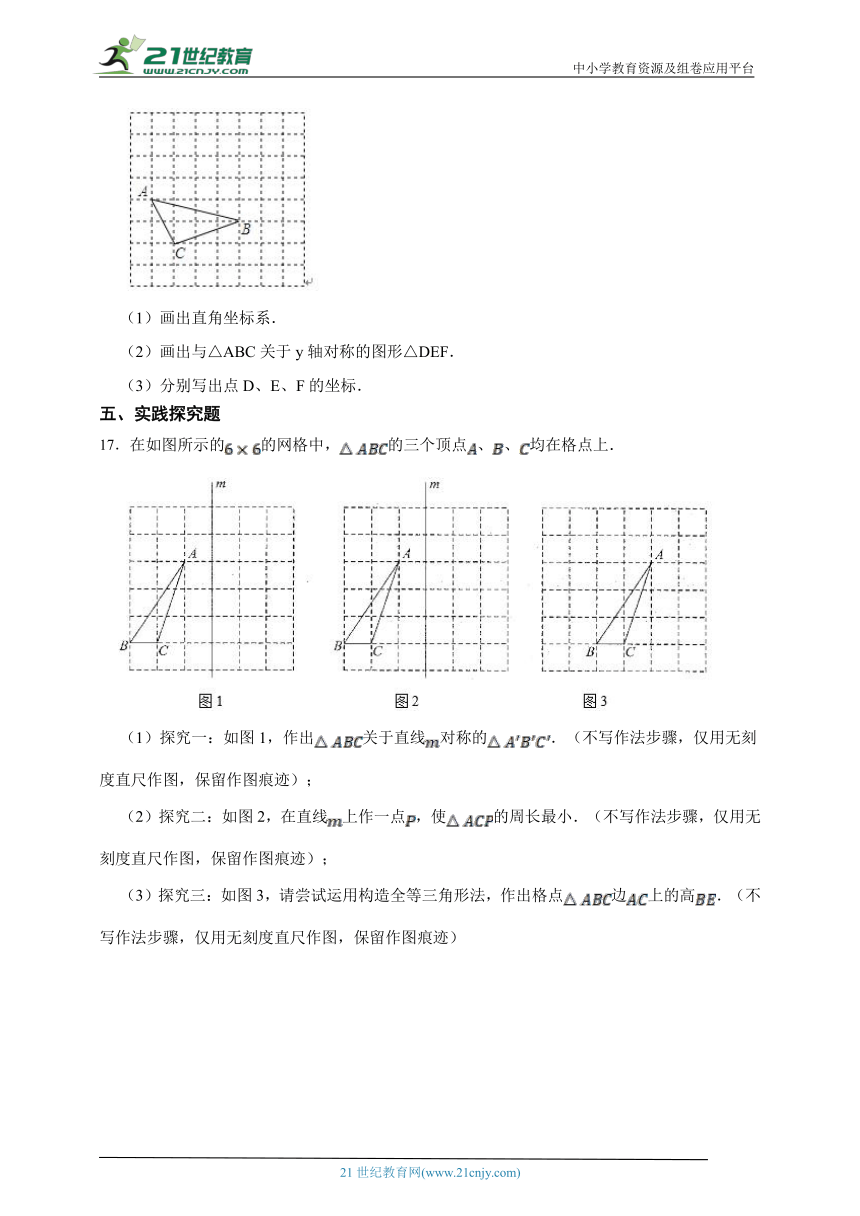
17.在如图所示的的网格中,的三个顶点、、均在格点上.
(1)探究一:如图1,作出关于直线对称的.(不写作法步骤,仅用无刻度直尺作图,保留作图痕迹);
(2)探究二:如图2,在直线上作一点,使的周长最小.(不写作法步骤,仅用无刻度直尺作图,保留作图痕迹);
(3)探究三:如图3,请尝试运用构造全等三角形法,作出格点边上的高.(不写作法步骤,仅用无刻度直尺作图,保留作图痕迹)
答案解析部分
1.【答案】C
【知识点】轴对称图形
2.【答案】B
【知识点】轴对称图形
3.【答案】C
【知识点】轴对称图形
4.【答案】B
【知识点】轴对称图形
5.【答案】B
【知识点】轴对称的应用-最短距离问题
6.【答案】
【知识点】三角形内角和定理;轴对称的性质
7.【答案】100
【知识点】三角形内角和定理;轴对称的性质
8.【答案】(-1,-1);(-2,1);(-2019,-1)
【知识点】轴对称的性质;平移的性质
9.【答案】2.5
【知识点】线段垂直平分线的性质;轴对称的应用-最短距离问题
10.【答案】
【知识点】轴对称的应用-最短距离问题
11.【答案】解:∵两个四边形关于某直线对称,
∴∠F=∠B=70°,EF=BC=4,
即x=70°,y=4.
【知识点】轴对称的性质
12.【答案】解:提供以下方案供参考.
【知识点】作图﹣轴对称
13.【答案】(1)解:轴对称图形如图1所示
(2)解:点A如图2所示
(3)解:点M如图3所示.
【知识点】作图﹣轴对称
14.【答案】解:(1)如图所示,△A1B1C1即为所求;
(2)△ABC的面积=3×3﹣ ×2×3﹣ ×1×2﹣ ×1×3= ;
(3)如图所示,点P即为所求.
【知识点】三角形的面积;作图﹣轴对称;轴对称的应用-最短距离问题
15.【答案】(1)解:A(0,3),B(﹣4,4),C(﹣2,1)
(2)△A1B1C1如图所示,B1(4,4).
【知识点】作图﹣轴对称
16.【答案】(1)解:所作图形如图所示:
(2)解:所作图形如图所示:
(3)解:D(3,1),E(﹣1,0),F(2,﹣1).
【知识点】作图﹣轴对称
17.【答案】(1)解:根据题意以及网格的特点直接作出关于直线对称的,如图所示;
(2)解:作点关于直线对称点,连接,交于点,如图所示;
则的周长
点即为所求;
(3)解:延长交于点,则即为所求,如图所示:
.,,
,
,
,
,
.
即为所求边上的高
【知识点】三角形的角平分线、中线和高;作图﹣轴对称;轴对称的应用-最短距离问题;三角形全等的判定(SAS)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【浙教版八上同步练习】
2.1图形的轴对称
一、单选题
1.在一些汉字的美术字中,有的是轴对称图形.下面五个词中“自由 平等 民主 敬业 友善”可以看作轴对称图形的汉字有 个.( )
A.2个 B.3个 C.4个 D.5个
2.一个企业的logo(标志)代表着一种精神,一种企业文化,以下是深圳市四个公司的logo,其中是轴对称图形的是( )
A. B.
C. D.
3.下列“QQ表情”中,属于轴对称图形的是 ( )
A. B. C. D.
4.人有忧喜,岁分四季,而在四季里,又分风、云、雨、雪、霜、露、虹、雾、雷等多种天气,可谓是气象万千,变幻莫测,下面是常用的天气符号,图片上有图案和文字说明,其中的图案不是轴对称图形的是( )
A.霜冻 B.雷雨
C.雾 D.小雪
5.如图,对角线AC将正方形ABCD分成两个等腰三角形,点E,F将对角线AC三等分,且AC=15,点P在正方形的边上,则满足PE+PF=5 的点P的个数是( )
A.0 B.4 C.8 D.16
二、填空题
6.如图, , , 与 关于直线l对称,则∠B= .
7.如图,△ABC与△A′B′C′关于直线 对称,则∠B的度数为 °
8.如图,已知点 .规定“把点 先作关于 轴对称,再向左平移1个单位”为一次变换.经过第一次变换后,点 的坐标为 ;经过第二次变换后,点 的坐标为 ;那么连续经过2019次变换后,点 的坐标为 .
9.如图,在△ABC中,∠BCA=120°,∠A=15°,AC=5,点M、N分别是AB、AC上动点,则CM+MN的最小值为 .
10.如图,正方形ABCD中,AB=2,连接AC,∠ACD的平分线交AD于点E,在AB上截取AF=DE,连接DF,分别交CE,AC于点G,H,点P是线段GC上的动点,PQ⊥AC于点Q,连接PH,则PH+PQ的最小值是 .
三、解答题
11.如图,这两个四边形关于某直线对称,根据图形的条件求x,y.
12.如图,有两个 7×4 的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
①线段的一个端点为梯形的顶点,另一个端点在梯形一边的格点上;
②将梯形分成两个图形,其中一个是轴对称图形;
③图1、图2中分成的轴对称图形不全等.
13.作图题:(不写作法,但要保留痕迹)
(1)作出图1形关于直线l的轴对称图形.
(2)在图2中找出点A,使它到M,N两点的距离相等,并且到OH,OF的距离相等.
(3)在图3中找到一点M,使它到A、B两点的距离和最小.
四、综合题
14.如图,在长度为1个单位长度的小正方形组成的正方形网格中, ABC的三个顶点A、B、C都在格点上.
( 1 )在图中画出与 ABC关于直线y成轴对称的 A1B1C1;
( 2 )求 ABC的面积;
( 3 )在x轴上找出一点P,使得PB+PC的值最小.(不需计算,在图上直接标记出点P的位置)
15.△ABC在直角坐标系内的位置如图.
(1)分别写出A、B、C的坐标
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标
16.如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(﹣2,﹣1)表示C点的位置,用(1,0)表示B点的位置,那么:
(1)画出直角坐标系.
(2)画出与△ABC关于y轴对称的图形△DEF.
(3)分别写出点D、E、F的坐标.
五、实践探究题
17.在如图所示的的网格中,的三个顶点、、均在格点上.
(1)探究一:如图1,作出关于直线对称的.(不写作法步骤,仅用无刻度直尺作图,保留作图痕迹);
(2)探究二:如图2,在直线上作一点,使的周长最小.(不写作法步骤,仅用无刻度直尺作图,保留作图痕迹);
(3)探究三:如图3,请尝试运用构造全等三角形法,作出格点边上的高.(不写作法步骤,仅用无刻度直尺作图,保留作图痕迹)
答案解析部分
1.【答案】C
【知识点】轴对称图形
2.【答案】B
【知识点】轴对称图形
3.【答案】C
【知识点】轴对称图形
4.【答案】B
【知识点】轴对称图形
5.【答案】B
【知识点】轴对称的应用-最短距离问题
6.【答案】
【知识点】三角形内角和定理;轴对称的性质
7.【答案】100
【知识点】三角形内角和定理;轴对称的性质
8.【答案】(-1,-1);(-2,1);(-2019,-1)
【知识点】轴对称的性质;平移的性质
9.【答案】2.5
【知识点】线段垂直平分线的性质;轴对称的应用-最短距离问题
10.【答案】
【知识点】轴对称的应用-最短距离问题
11.【答案】解:∵两个四边形关于某直线对称,
∴∠F=∠B=70°,EF=BC=4,
即x=70°,y=4.
【知识点】轴对称的性质
12.【答案】解:提供以下方案供参考.
【知识点】作图﹣轴对称
13.【答案】(1)解:轴对称图形如图1所示
(2)解:点A如图2所示
(3)解:点M如图3所示.
【知识点】作图﹣轴对称
14.【答案】解:(1)如图所示,△A1B1C1即为所求;
(2)△ABC的面积=3×3﹣ ×2×3﹣ ×1×2﹣ ×1×3= ;
(3)如图所示,点P即为所求.
【知识点】三角形的面积;作图﹣轴对称;轴对称的应用-最短距离问题
15.【答案】(1)解:A(0,3),B(﹣4,4),C(﹣2,1)
(2)△A1B1C1如图所示,B1(4,4).
【知识点】作图﹣轴对称
16.【答案】(1)解:所作图形如图所示:
(2)解:所作图形如图所示:
(3)解:D(3,1),E(﹣1,0),F(2,﹣1).
【知识点】作图﹣轴对称
17.【答案】(1)解:根据题意以及网格的特点直接作出关于直线对称的,如图所示;
(2)解:作点关于直线对称点,连接,交于点,如图所示;
则的周长
点即为所求;
(3)解:延长交于点,则即为所求,如图所示:
.,,
,
,
,
,
.
即为所求边上的高
【知识点】三角形的角平分线、中线和高;作图﹣轴对称;轴对称的应用-最短距离问题;三角形全等的判定(SAS)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
