[浙教版八上同步练习] 第二章特殊三角形检测题(培优)(含答案)
文档属性
| 名称 | [浙教版八上同步练习] 第二章特殊三角形检测题(培优)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-27 16:53:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
[浙教版八上同步练习]
第二章特殊三角形检测题(培优)
一、单选题
1.对称现象无处不在,请你观察下面的四个图形,它们体现了中华民族的传统文化,其中,可以看作是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
2.一张薄纸,一双巧手,在一剪一刻间幻化出千姿百态的美丽图案,令人叹为观止,这就是剪纸艺术.佛山剪纸,流传于广东省佛山市的传统美术,是国家级第一批非物质文化遗产之一.剪纸作品形式多样,以下剪纸作品中不是轴对称图形的是( )
A. B.
C. D.
3.已知等腰三角形的一边长等于4,一边长等于8,则它的周长为( )
A.9 B.16或20 C.16 D.20
4.已知一个直角三角形三边长的平方和为800,则斜边长为( )
A.10 B.20 C.30 D.40
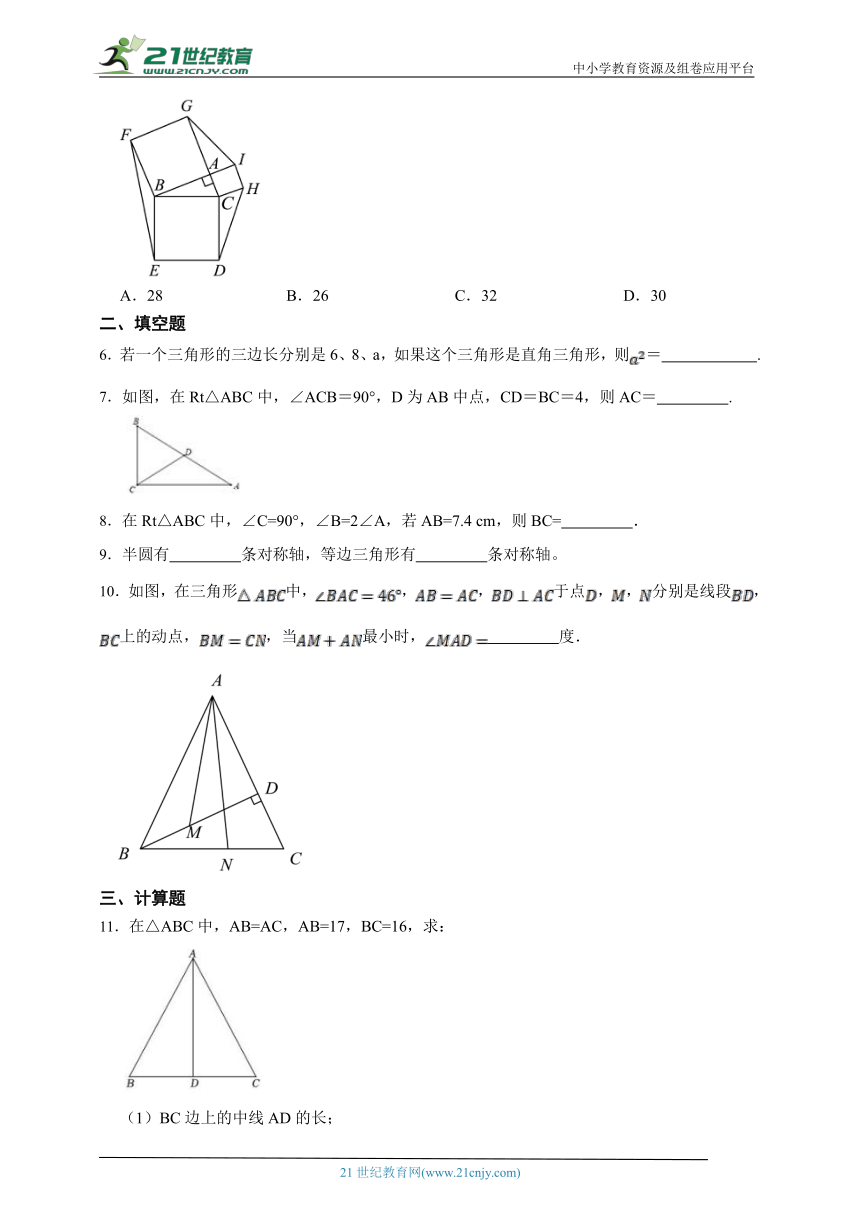
5.勾股定理又称毕达哥拉斯定理、商高定理、百牛定理,是人类早期发现并证明的重要数学定理之一、如图,在中,,以各边为边向外作正方形、正方形、正方形.连接、、,若,,则这个六边形的面积为( )
A.28 B.26 C.32 D.30
二、填空题
6.若一个三角形的三边长分别是6、8、a,如果这个三角形是直角三角形,则= .
7.如图,在Rt△ABC中,∠ACB=90°,D为AB中点,CD=BC=4,则AC= .
8.在Rt△ABC中,∠C=90°,∠B=2∠A,若AB=7.4 cm,则BC= .
9.半圆有 条对称轴,等边三角形有 条对称轴。
10.如图,在三角形中,,,于点,,分别是线段,上的动点,,当最小时, 度.
三、计算题
11.在△ABC中,AB=AC,AB=17,BC=16,求:
(1)BC边上的中线AD的长;
(2)△ABC的面积.
四、解答题
12.如图,一架长的梯子斜靠在一竖直的墙上,这时为,如果梯子的顶端A尚墙下滑,那么梯子底端B向外移了多少米?(注意:)
13.如图,在中,,是边上的中线,点是边上的一个动点,点是上的一个动点.
(1)当时,求的度数;
(2)若,,.
①求中边上的高;
②当的值最小时,最小值是 ▲ .
五、综合题
14.如图,AB∥CD,CE平分∠ACD交AB于点E.
(1)求证:△ACE是等腰三角形.
(2)若AC=13,CE=10,求△ACE的面积.
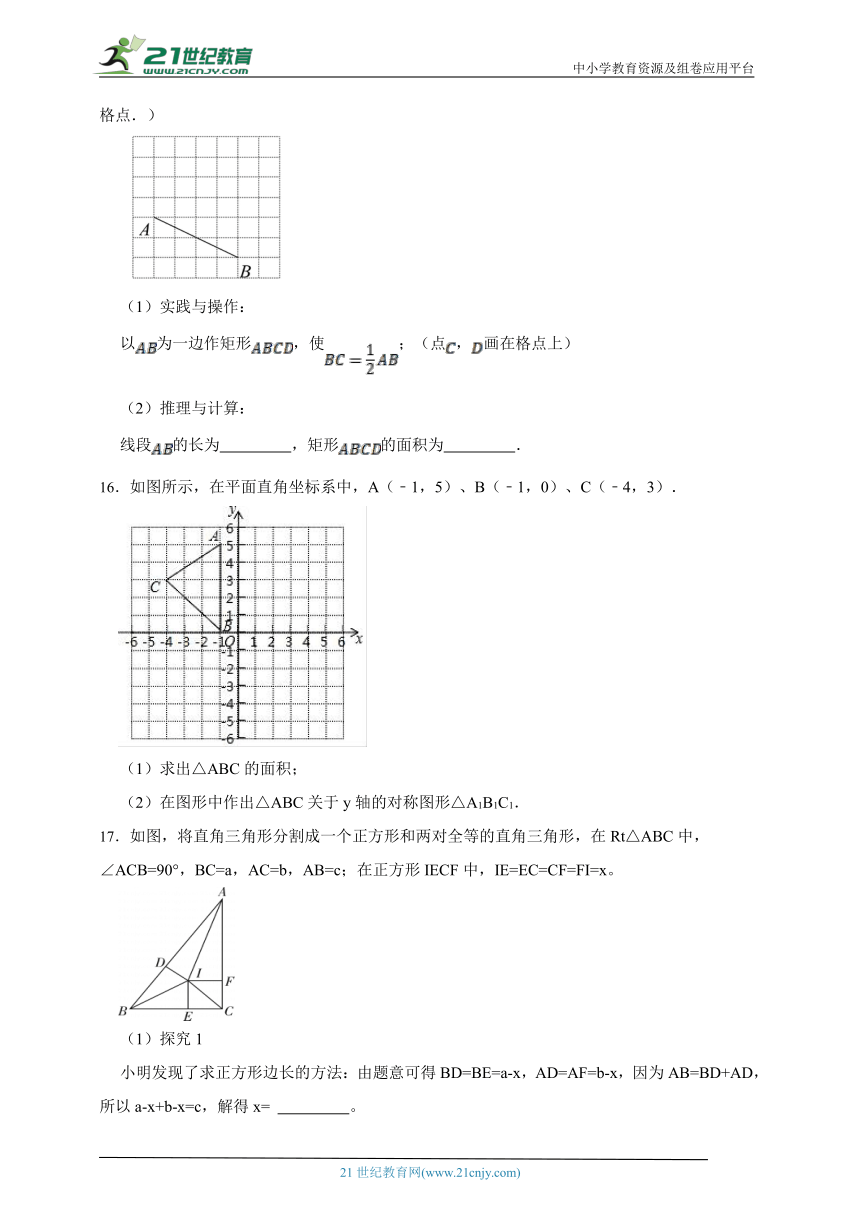
15.如图,在边长均为1的小正方形网格中,线段的端点都在格点上.(小正方形的顶点叫格点.)
(1)实践与操作:
以为一边作矩形,使;(点,画在格点上)
(2)推理与计算:
线段的长为 ,矩形的面积为 .
16.如图所示,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3).
(1)求出△ABC的面积;
(2)在图形中作出△ABC关于y轴的对称图形△A1B1C1.
17.如图,将直角三角形分割成一个正方形和两对全等的直角三角形,在Rt△ABC中,∠ACB=90°,BC=a,AC=b,AB=c;在正方形IECF中,IE=EC=CF=FI=x。
(1)探究1
小明发现了求正方形边长的方法:由题意可得BD=BE=a-x,AD=AF=b-x,因为AB=BD+AD,所以a-x+b-x=c,解得x= 。
(2)探究2
小亮发现了另一种求正方形边长的方法:连接IC,利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系.请根据小亮的思路完成他的求解过程。
(3)探究3
请结合小明和小亮得到的结论验证勾股定理(注:根据比例的基本性质,由 可得ad=bc)。
六、实践探究题
18.阅读材料并解答问题:
关于勾股定理的研究有一个很重要的内容是勾股数组,在数学课本中我们已经了解到,“能够成为直角三角形三条边的三个正整数称为勾股数”,以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法:
方法1:若m为奇数(m≥3),则a=m,b= (m2﹣1)和c= (m2+1)是勾股数.
方法2:若任取两个正整数m和n(m>n),则a=m2﹣n2,b=2mn,c=m2+n2是勾股数.
(1)在以上两种方法中任选一种,证明以a,b,c为边长的△ABC是直角三角形;
(2)某园林管理处要在一块绿地上植树,使之构成如下图所示的图案景观,该图案由四个全等的直角三角形组成,要求每个三角形顶点处都植一棵树,各边上相邻两棵树之间的距离均为1米,如果每个三角形最短边上都植6棵树,且每个三角形的各边长之比为5:12:13,那么这四个直角三角形的边长共需植树 棵.
(3)某家俱市场现有大批如图所示的梯形边角余料(单位:cm),实验初中数学兴趣小组决定将其加工成等腰三角形,且方案如下:
三角形中至少有一边长为10 cm; 三角形中至少有一边上的高为8 cm,
请设计出三种面积不同的方案并在图上画出分割线,求出相应图形面积.
答案解析部分
1.【答案】D
【知识点】轴对称图形
2.【答案】D
【知识点】轴对称图形
3.【答案】D
【知识点】三角形三边关系;等腰三角形的性质
4.【答案】B
【知识点】勾股定理
5.【答案】A
【知识点】勾股定理的应用
6.【答案】100或28
【知识点】勾股定理
7.【答案】
【知识点】勾股定理;直角三角形斜边上的中线
8.【答案】3.7 cm
【知识点】含30°角的直角三角形
9.【答案】1;3
【知识点】轴对称图形
10.【答案】
【知识点】三角形全等及其性质;等腰三角形的性质
11.【答案】(1)解:在△ABC中,AB=AC,AD是△ABC的高线,AB=17,BC=16,
∴BD=BC=×16=8,
∴AD===15.
(2)由面积计算公式得
∴
【知识点】三角形的角平分线、中线和高;三角形的面积;勾股定理
12.【答案】解:中,,,
;
同理,中,
,,
,
.
答:梯子底端B向外移了.
【知识点】勾股定理的应用
13.【答案】(1)解:,是边上的中线,
,,
,
;
(2)解:①设中边上的高为,
,
,
,
即中边上的高为;
②
【知识点】垂线段最短;三角形的面积;等腰三角形的性质;轴对称的应用-最短距离问题
14.【答案】(1)证明: ∵ CE平分∠ACD,∴∠ACE = ∠ECD.
∵ AB // CD,∴∠AEC = ∠ECD,∴∠ACE = ∠AEC,∴△ACE是等腰三角形
(2)解:过A作AG⊥CE,垂足为G.∵AC=AE,∴CG=EG= CE=5(cm).
∵AC=13(cm),由勾股定理得,AG=5(cm),∴S△ACE= ×24×5=60(cm2)
【知识点】等腰三角形的判定与性质;勾股定理
15.【答案】(1)解:如图,矩形为所求图形;
(2);10
【知识点】勾股定理的应用
16.【答案】(1)解:△ABC的面积= ×5×3=7.5
(2)解:如图,△A1B1C1即为所作.
【知识点】作图﹣轴对称
17.【答案】(1)
(2)解:∵S△ABC=S△ABI++S△BIC+S△AIC
∴ ab= cx+ ax+ bx,∴ x=
(3)解:根据(1)和(2)得x= ,即2ab=(a+b+c)(a+b-c),
化简得a2+b2=c2…
【知识点】三角形的面积;勾股定理的证明
18.【答案】(1)解:方法1、c-a= (m2+1)-m= (m2-2m+1)= (m-1)2>0,c-b=1>0,
所以c>a,c>b.而a2+b2=m2+[ (m2-1)]2=( m4-2m2+1)+m2
= (m4+2m2+1)=[ (m2+1)]2=c2,
所以以a、b、c为边的三角形是直角三角形
(2)解:120
(3)解: 由勾股定理得:AB= 则
如图(1)AD=AB=10 cm时,BD=6 cm,S = =48 cm ;
如图(2)BD=AB=10 cm时,S = =40cm ; 如图(3)线段AB的垂直平分线交BC延长线于点D,则AB=10,设DC=x,则AD=BD=6+x,在Rt△ACD中 ,S = = ;答:面积分别为48 cm 、40cm 和 cm 的等腰三角形
【知识点】勾股定理的逆定理;勾股定理的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
[浙教版八上同步练习]
第二章特殊三角形检测题(培优)
一、单选题
1.对称现象无处不在,请你观察下面的四个图形,它们体现了中华民族的传统文化,其中,可以看作是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
2.一张薄纸,一双巧手,在一剪一刻间幻化出千姿百态的美丽图案,令人叹为观止,这就是剪纸艺术.佛山剪纸,流传于广东省佛山市的传统美术,是国家级第一批非物质文化遗产之一.剪纸作品形式多样,以下剪纸作品中不是轴对称图形的是( )
A. B.
C. D.
3.已知等腰三角形的一边长等于4,一边长等于8,则它的周长为( )
A.9 B.16或20 C.16 D.20
4.已知一个直角三角形三边长的平方和为800,则斜边长为( )
A.10 B.20 C.30 D.40
5.勾股定理又称毕达哥拉斯定理、商高定理、百牛定理,是人类早期发现并证明的重要数学定理之一、如图,在中,,以各边为边向外作正方形、正方形、正方形.连接、、,若,,则这个六边形的面积为( )
A.28 B.26 C.32 D.30
二、填空题
6.若一个三角形的三边长分别是6、8、a,如果这个三角形是直角三角形,则= .
7.如图,在Rt△ABC中,∠ACB=90°,D为AB中点,CD=BC=4,则AC= .
8.在Rt△ABC中,∠C=90°,∠B=2∠A,若AB=7.4 cm,则BC= .
9.半圆有 条对称轴,等边三角形有 条对称轴。
10.如图,在三角形中,,,于点,,分别是线段,上的动点,,当最小时, 度.
三、计算题
11.在△ABC中,AB=AC,AB=17,BC=16,求:
(1)BC边上的中线AD的长;
(2)△ABC的面积.
四、解答题
12.如图,一架长的梯子斜靠在一竖直的墙上,这时为,如果梯子的顶端A尚墙下滑,那么梯子底端B向外移了多少米?(注意:)
13.如图,在中,,是边上的中线,点是边上的一个动点,点是上的一个动点.
(1)当时,求的度数;
(2)若,,.
①求中边上的高;
②当的值最小时,最小值是 ▲ .
五、综合题
14.如图,AB∥CD,CE平分∠ACD交AB于点E.
(1)求证:△ACE是等腰三角形.
(2)若AC=13,CE=10,求△ACE的面积.
15.如图,在边长均为1的小正方形网格中,线段的端点都在格点上.(小正方形的顶点叫格点.)
(1)实践与操作:
以为一边作矩形,使;(点,画在格点上)
(2)推理与计算:
线段的长为 ,矩形的面积为 .
16.如图所示,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3).
(1)求出△ABC的面积;
(2)在图形中作出△ABC关于y轴的对称图形△A1B1C1.
17.如图,将直角三角形分割成一个正方形和两对全等的直角三角形,在Rt△ABC中,∠ACB=90°,BC=a,AC=b,AB=c;在正方形IECF中,IE=EC=CF=FI=x。
(1)探究1
小明发现了求正方形边长的方法:由题意可得BD=BE=a-x,AD=AF=b-x,因为AB=BD+AD,所以a-x+b-x=c,解得x= 。
(2)探究2
小亮发现了另一种求正方形边长的方法:连接IC,利用S△ABC=S△AIB+S△AIC+S△BIC可以得到x与a、b、c的关系.请根据小亮的思路完成他的求解过程。
(3)探究3
请结合小明和小亮得到的结论验证勾股定理(注:根据比例的基本性质,由 可得ad=bc)。
六、实践探究题
18.阅读材料并解答问题:
关于勾股定理的研究有一个很重要的内容是勾股数组,在数学课本中我们已经了解到,“能够成为直角三角形三条边的三个正整数称为勾股数”,以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法:
方法1:若m为奇数(m≥3),则a=m,b= (m2﹣1)和c= (m2+1)是勾股数.
方法2:若任取两个正整数m和n(m>n),则a=m2﹣n2,b=2mn,c=m2+n2是勾股数.
(1)在以上两种方法中任选一种,证明以a,b,c为边长的△ABC是直角三角形;
(2)某园林管理处要在一块绿地上植树,使之构成如下图所示的图案景观,该图案由四个全等的直角三角形组成,要求每个三角形顶点处都植一棵树,各边上相邻两棵树之间的距离均为1米,如果每个三角形最短边上都植6棵树,且每个三角形的各边长之比为5:12:13,那么这四个直角三角形的边长共需植树 棵.
(3)某家俱市场现有大批如图所示的梯形边角余料(单位:cm),实验初中数学兴趣小组决定将其加工成等腰三角形,且方案如下:
三角形中至少有一边长为10 cm; 三角形中至少有一边上的高为8 cm,
请设计出三种面积不同的方案并在图上画出分割线,求出相应图形面积.
答案解析部分
1.【答案】D
【知识点】轴对称图形
2.【答案】D
【知识点】轴对称图形
3.【答案】D
【知识点】三角形三边关系;等腰三角形的性质
4.【答案】B
【知识点】勾股定理
5.【答案】A
【知识点】勾股定理的应用
6.【答案】100或28
【知识点】勾股定理
7.【答案】
【知识点】勾股定理;直角三角形斜边上的中线
8.【答案】3.7 cm
【知识点】含30°角的直角三角形
9.【答案】1;3
【知识点】轴对称图形
10.【答案】
【知识点】三角形全等及其性质;等腰三角形的性质
11.【答案】(1)解:在△ABC中,AB=AC,AD是△ABC的高线,AB=17,BC=16,
∴BD=BC=×16=8,
∴AD===15.
(2)由面积计算公式得
∴
【知识点】三角形的角平分线、中线和高;三角形的面积;勾股定理
12.【答案】解:中,,,
;
同理,中,
,,
,
.
答:梯子底端B向外移了.
【知识点】勾股定理的应用
13.【答案】(1)解:,是边上的中线,
,,
,
;
(2)解:①设中边上的高为,
,
,
,
即中边上的高为;
②
【知识点】垂线段最短;三角形的面积;等腰三角形的性质;轴对称的应用-最短距离问题
14.【答案】(1)证明: ∵ CE平分∠ACD,∴∠ACE = ∠ECD.
∵ AB // CD,∴∠AEC = ∠ECD,∴∠ACE = ∠AEC,∴△ACE是等腰三角形
(2)解:过A作AG⊥CE,垂足为G.∵AC=AE,∴CG=EG= CE=5(cm).
∵AC=13(cm),由勾股定理得,AG=5(cm),∴S△ACE= ×24×5=60(cm2)
【知识点】等腰三角形的判定与性质;勾股定理
15.【答案】(1)解:如图,矩形为所求图形;
(2);10
【知识点】勾股定理的应用
16.【答案】(1)解:△ABC的面积= ×5×3=7.5
(2)解:如图,△A1B1C1即为所作.
【知识点】作图﹣轴对称
17.【答案】(1)
(2)解:∵S△ABC=S△ABI++S△BIC+S△AIC
∴ ab= cx+ ax+ bx,∴ x=
(3)解:根据(1)和(2)得x= ,即2ab=(a+b+c)(a+b-c),
化简得a2+b2=c2…
【知识点】三角形的面积;勾股定理的证明
18.【答案】(1)解:方法1、c-a= (m2+1)-m= (m2-2m+1)= (m-1)2>0,c-b=1>0,
所以c>a,c>b.而a2+b2=m2+[ (m2-1)]2=( m4-2m2+1)+m2
= (m4+2m2+1)=[ (m2+1)]2=c2,
所以以a、b、c为边的三角形是直角三角形
(2)解:120
(3)解: 由勾股定理得:AB= 则
如图(1)AD=AB=10 cm时,BD=6 cm,S = =48 cm ;
如图(2)BD=AB=10 cm时,S = =40cm ; 如图(3)线段AB的垂直平分线交BC延长线于点D,则AB=10,设DC=x,则AD=BD=6+x,在Rt△ACD中 ,S = = ;答:面积分别为48 cm 、40cm 和 cm 的等腰三角形
【知识点】勾股定理的逆定理;勾股定理的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
