八年级下每日一题76-80平行四边形的性质的性质与判定综合(含解析)
文档属性
| 名称 | 八年级下每日一题76-80平行四边形的性质的性质与判定综合(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-29 05:14:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
每日一题76 平行四边形的性质与判定综合
班级 姓名 学号
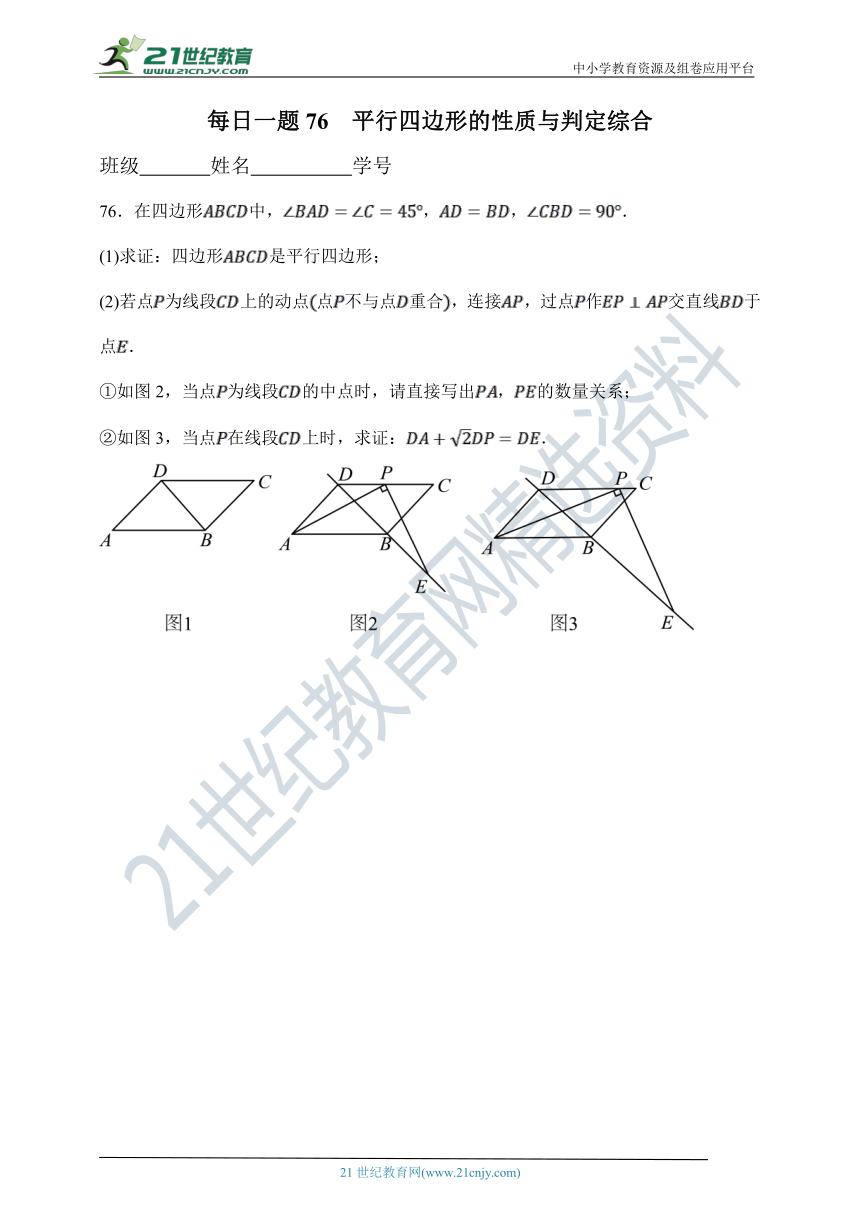
76.在四边形中,,,.
(1)求证:四边形是平行四边形;
(2)若点为线段上的动点点不与点重合,连接,过点作交直线于点.
①如图2,当点为线段的中点时,请直接写出,的数量关系;
②如图3,当点在线段上时,求证:.
每日一题77 平行四边形的性质与判定综合
班级 姓名 学号
77.如图1,在中,,,,点P,Q分别是上的动点,P从C出发以每秒3个单位长度的速度向终点A运动,Q从A出发以每秒8个单位长度的速度向终点B运动,两点同时出发,当其中一点到达终点时整个运动结束,设运动时间为t秒.过点Q作于点M.
(1)______,______.(用含t的代数式表示)
(2)如图2,已知点D为中点,连接,以为邻边作平行四边形.
①当时,求的长;
②在运动过程中,是否存在某一时刻,使得平行四边形的一边落在的某边上?若存在,求出所有符合条件的t的值;若不存在,请说明理由.
每日一题78 平行四边形的性质与判定综合
班级 姓名 学号
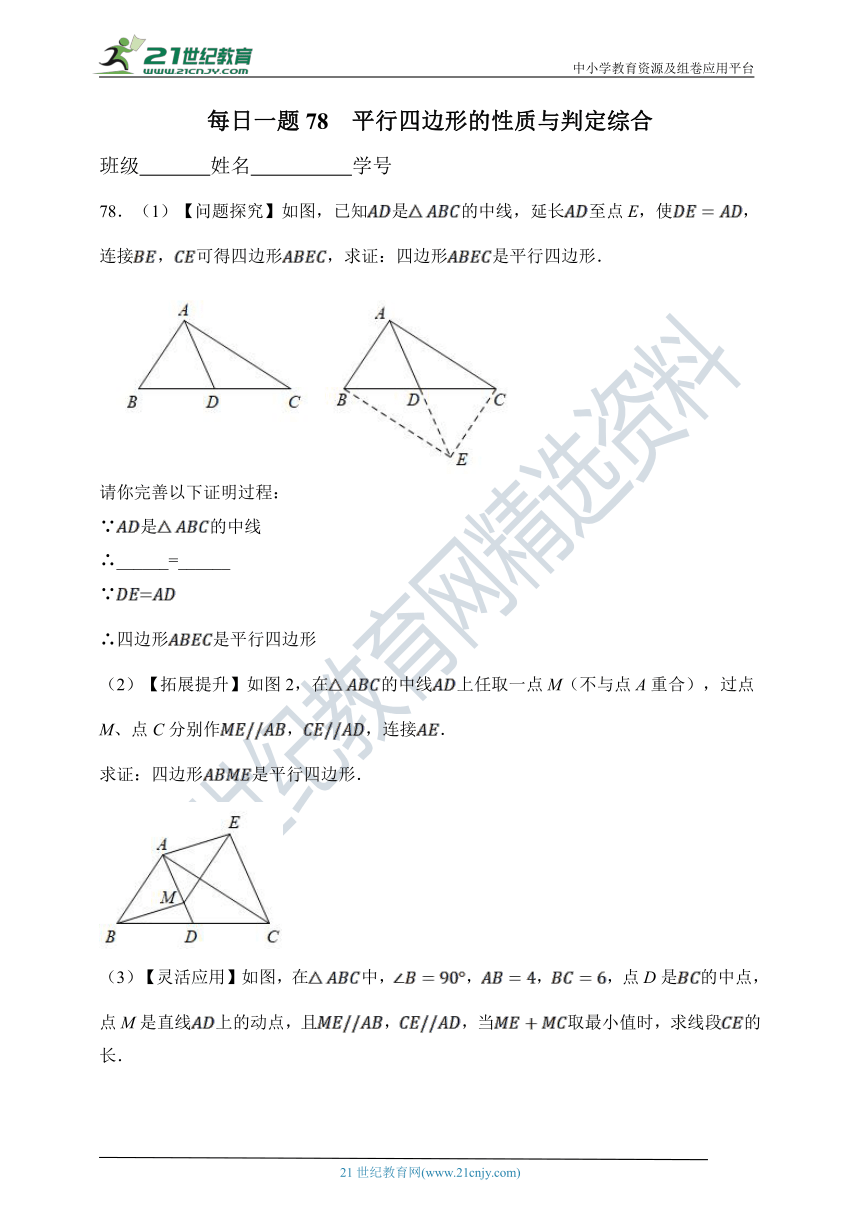
78.(1)【问题探究】如图,已知是的中线,延长至点E,使,连接,可得四边形,求证:四边形是平行四边形.
请你完善以下证明过程:
∵是的中线
∴______=______
∵
∴四边形是平行四边形
(2)【拓展提升】如图2,在的中线上任取一点M(不与点A重合),过点M、点C分别作,,连接.
求证:四边形是平行四边形.
(3)【灵活应用】如图,在中,,,,点D是的中点,点M是直线上的动点,且,,当取最小值时,求线段的长.
每日一题79 平行四边形的性质与判定综合
班级 姓名 学号
79.如图,以的三边为边在BC的同侧作等边、、,请回答下列问题:
(1)求证:四边形ADEF为平行四边形:
(2)当满足什么条件时,以A、D、E、F为顶点的四边形不存在,并说明理由:
(3)如图(2),若,,AB和AC的长为一元二次方程的两个根,求四边形ADEF的面积.
每日一题80 平行四边形的性质与判定综合
班级 姓名 学号
80.如图,在四边形中,,,,,,动点N从点D出发,以每秒的速度在射线上运动到C点返回,动点M从点A出发,在线段上,以每秒的速度向点B运动,点M,N分别从点A,D同时出发.当点M运动到点B时,点N随之停止运动,设运动时间为t(秒).
(1)当t为何值时,四边形是平行四边形.
(2)是否存在点N,使是等腰三角形?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
每日一题76 答案
76.【详解】(1)证明:,,
,,
,,,
,,,,,
,四边形是平行四边形;
(2)解:①,
理由如下:连接,如图所示:
由(1)知是等腰直角三角形,当点为线段的中点时,,,
,
,
,
,
,
,
,
,
;
②证明:过点作交于点,如图所示:
,,
,
,
四边形是平行四边形,
,,
又,
,
,
,
,
,
,
,
,
在中,,则,
,
.
每日一题77 答案
77.【详解】(1)解:∵在中,,,,
∴,
∵P从C出发以每秒3个单位长度的速度向终点A运动,Q从A出发以每秒8个单位长度的速度向终点B运动,∴,
∴,
∵,∴,
又∵,∴,
故答案为:,;
(2)解:①∵,∴,解得,
∴,∴,
在中,由勾股定理得,
∵点D为中点,∴,
∴,
在中,由勾股定理得;
②如图2-1所示,当落在上时,则,∴,
∴此时点D与点M重合,∴,
在中,由勾股定理得,
∴,解得或(舍去);
如图2-2所示,当落在上时,延长到H使得,连接,∵,
∴,∴,∴,
∵四边形是平行四边形,∴,
∴四边形是平行四边形,∴,
∴,解得;
如图2-3所示,当点Q运动到点B时,此时在上,
∴;
综上所述,t的值为或2或3.
每日一题78 答案
78.【详解】(1)解:∵是的中线,∴,
∵,∴四边形是平行四边形.
故答案为:,;
(2)证明:如图,延长至点F,使,连接CF,BF,
∵是的中线,
∴,
∵,
∴四边形是平行四边形.
∴,,
∵,
∴,
又∵,
∴四边形是平行四边形.
∴,
∴,
∴四边形是平行四边形.
(3)解:如图所示,连接AE,BM,延长DM至点N,使,连接CN,BN.
∵点D是的中点,
∴,
又∵,,
∴.
同(2)可证,四边形是平行四边形,
∴,
∴当MC取最小值时,取最小值,
∵,
∴时,MC取最小值.
同(1)可证四边形是平行四边形,
∴,,,
∵,,
∴,
∴,
即,
∴,
又∵在中,,,
∴.
故线段CE的长为.
每日一题79 答案
79.【详解】解:(1)∵△ABD,△EBC都是等边三角形.
∴AD=BD=AB,BC=BE=EC,∠DBA=∠EBC=60°
∴∠DBE+∠EBA=∠ABC+∠EBA.∴∠DBE=∠ABC.
在△DBE和△ABC中,∵BD=BA,∠DBE=∠ABC,BE=BC,
∴△DBE≌△ABC(SAS).∴DE=AC.
又∵△ACF是等边三角形,∴AC=AF.∴DE=AF.
同理可证:AD=EF,∴四边形ADEF平行四边形;
(2)当∠BAC=60°时,以D、A、E、F为顶点的四边形不存在;理由如下:
∵∠BAC=60°,∠BAD=∠CAE=60°,
∴∠DAF=360°-∠DAB-∠BAC-∠CAF=180°,∴点D、A、F共线,
∴以D、A、E、F为顶点的四边形不存在;
(3)过点A作AH⊥DE于点H,
∵AB和AC的长为一元二次方程的两根,
∴,①
,②
①+②,得:,
在Rt△ABC中,∵BC=,∴,AB+AC==10,
∴有,解得:m=24,
∴原方程为,
解得:,,
若AB=6,AC=4,
∵四边形ABCD是平行四边形,
∴DE∥AF,DE=AF=AC=4,AD=EF=AB=6,
∴∠ADE+∠DAF=180°,
∵∠DAF=360°-60°-60°-90°=150°,
∴∠ADE=30°,∴AH=AD=3,
∴S平行四边形ADEF=DE×AH=12;
若AB=4,AC=6,
∵四边形ABCD是平行四边形,
∴DE∥AF,DE=AF=AC=6,AD=EF=AB=4,
∴∠ADE+∠DAF=180°,
∵∠DAF=360°-60°-60°-90°=150°,
∴∠ADE=30°,∴AH=AD=2,
∴S平行四边形ADEF=DE×AH=12;
综上:四边形ADEF的面积为12.
每日一题80 答案
80.【详解】解:(1)设运动时间为t秒.
∵四边形MNCB是平行四边形,∴MB=NC,
当N从D运动到C时,
∵BC=13cm,CD=21cm,∴BM=AB-AM=16-t,CN=21-2t,
∴16-t=21-2t,解得t=5,
当N从C运动到D时,∵BM=AB-AM=16-t,CN=2t-21
∴16-t=2t-21,解得t=,∴当t=5秒或秒时,四边形MNCB是平行四边形;
(2)△NMB是等腰三角形有三种情况,
Ⅰ.当NM=NB时,作NH⊥AB于H,则HM=HB,
当N从D运动到C时,∵MH=HB=BM=(16-t),
由AH=DN得2t=(16 t)+t,解得t=秒;
当点N从C向D运动时,观察图象可知,只有由题意:42-2t=(16-t)+t,
解得t=秒.
Ⅱ.当MN=MB,当N从D运动到C时,
MH=AH-AM=DN-AM=2t-t=t,BM=16-t,
∵MN2=t2+122,∴(16-t)2=122+t2,解得t=(秒);
Ⅲ.当BM=BN,当N从C运动到D时,
则BH=AB-AH=AB-DN=16-2t,
∵BM2=BN2=NH2+BH2=122+(16-2t)2,
∴(16-t)2=122+(16-2t)2,
即3t2-32t+144=0,
∵△<0,
∴方程无实根,
综上可知,当t=秒或秒或秒时,△BMN是等腰三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题76 平行四边形的性质与判定综合
班级 姓名 学号
76.在四边形中,,,.
(1)求证:四边形是平行四边形;
(2)若点为线段上的动点点不与点重合,连接,过点作交直线于点.
①如图2,当点为线段的中点时,请直接写出,的数量关系;
②如图3,当点在线段上时,求证:.
每日一题77 平行四边形的性质与判定综合
班级 姓名 学号
77.如图1,在中,,,,点P,Q分别是上的动点,P从C出发以每秒3个单位长度的速度向终点A运动,Q从A出发以每秒8个单位长度的速度向终点B运动,两点同时出发,当其中一点到达终点时整个运动结束,设运动时间为t秒.过点Q作于点M.
(1)______,______.(用含t的代数式表示)
(2)如图2,已知点D为中点,连接,以为邻边作平行四边形.
①当时,求的长;
②在运动过程中,是否存在某一时刻,使得平行四边形的一边落在的某边上?若存在,求出所有符合条件的t的值;若不存在,请说明理由.
每日一题78 平行四边形的性质与判定综合
班级 姓名 学号
78.(1)【问题探究】如图,已知是的中线,延长至点E,使,连接,可得四边形,求证:四边形是平行四边形.
请你完善以下证明过程:
∵是的中线
∴______=______
∵
∴四边形是平行四边形
(2)【拓展提升】如图2,在的中线上任取一点M(不与点A重合),过点M、点C分别作,,连接.
求证:四边形是平行四边形.
(3)【灵活应用】如图,在中,,,,点D是的中点,点M是直线上的动点,且,,当取最小值时,求线段的长.
每日一题79 平行四边形的性质与判定综合
班级 姓名 学号
79.如图,以的三边为边在BC的同侧作等边、、,请回答下列问题:
(1)求证:四边形ADEF为平行四边形:
(2)当满足什么条件时,以A、D、E、F为顶点的四边形不存在,并说明理由:
(3)如图(2),若,,AB和AC的长为一元二次方程的两个根,求四边形ADEF的面积.
每日一题80 平行四边形的性质与判定综合
班级 姓名 学号
80.如图,在四边形中,,,,,,动点N从点D出发,以每秒的速度在射线上运动到C点返回,动点M从点A出发,在线段上,以每秒的速度向点B运动,点M,N分别从点A,D同时出发.当点M运动到点B时,点N随之停止运动,设运动时间为t(秒).
(1)当t为何值时,四边形是平行四边形.
(2)是否存在点N,使是等腰三角形?若存在,请求出所有满足要求的t的值,若不存在,请说明理由.
每日一题76 答案
76.【详解】(1)证明:,,
,,
,,,
,,,,,
,四边形是平行四边形;
(2)解:①,
理由如下:连接,如图所示:
由(1)知是等腰直角三角形,当点为线段的中点时,,,
,
,
,
,
,
,
,
,
;
②证明:过点作交于点,如图所示:
,,
,
,
四边形是平行四边形,
,,
又,
,
,
,
,
,
,
,
,
在中,,则,
,
.
每日一题77 答案
77.【详解】(1)解:∵在中,,,,
∴,
∵P从C出发以每秒3个单位长度的速度向终点A运动,Q从A出发以每秒8个单位长度的速度向终点B运动,∴,
∴,
∵,∴,
又∵,∴,
故答案为:,;
(2)解:①∵,∴,解得,
∴,∴,
在中,由勾股定理得,
∵点D为中点,∴,
∴,
在中,由勾股定理得;
②如图2-1所示,当落在上时,则,∴,
∴此时点D与点M重合,∴,
在中,由勾股定理得,
∴,解得或(舍去);
如图2-2所示,当落在上时,延长到H使得,连接,∵,
∴,∴,∴,
∵四边形是平行四边形,∴,
∴四边形是平行四边形,∴,
∴,解得;
如图2-3所示,当点Q运动到点B时,此时在上,
∴;
综上所述,t的值为或2或3.
每日一题78 答案
78.【详解】(1)解:∵是的中线,∴,
∵,∴四边形是平行四边形.
故答案为:,;
(2)证明:如图,延长至点F,使,连接CF,BF,
∵是的中线,
∴,
∵,
∴四边形是平行四边形.
∴,,
∵,
∴,
又∵,
∴四边形是平行四边形.
∴,
∴,
∴四边形是平行四边形.
(3)解:如图所示,连接AE,BM,延长DM至点N,使,连接CN,BN.
∵点D是的中点,
∴,
又∵,,
∴.
同(2)可证,四边形是平行四边形,
∴,
∴当MC取最小值时,取最小值,
∵,
∴时,MC取最小值.
同(1)可证四边形是平行四边形,
∴,,,
∵,,
∴,
∴,
即,
∴,
又∵在中,,,
∴.
故线段CE的长为.
每日一题79 答案
79.【详解】解:(1)∵△ABD,△EBC都是等边三角形.
∴AD=BD=AB,BC=BE=EC,∠DBA=∠EBC=60°
∴∠DBE+∠EBA=∠ABC+∠EBA.∴∠DBE=∠ABC.
在△DBE和△ABC中,∵BD=BA,∠DBE=∠ABC,BE=BC,
∴△DBE≌△ABC(SAS).∴DE=AC.
又∵△ACF是等边三角形,∴AC=AF.∴DE=AF.
同理可证:AD=EF,∴四边形ADEF平行四边形;
(2)当∠BAC=60°时,以D、A、E、F为顶点的四边形不存在;理由如下:
∵∠BAC=60°,∠BAD=∠CAE=60°,
∴∠DAF=360°-∠DAB-∠BAC-∠CAF=180°,∴点D、A、F共线,
∴以D、A、E、F为顶点的四边形不存在;
(3)过点A作AH⊥DE于点H,
∵AB和AC的长为一元二次方程的两根,
∴,①
,②
①+②,得:,
在Rt△ABC中,∵BC=,∴,AB+AC==10,
∴有,解得:m=24,
∴原方程为,
解得:,,
若AB=6,AC=4,
∵四边形ABCD是平行四边形,
∴DE∥AF,DE=AF=AC=4,AD=EF=AB=6,
∴∠ADE+∠DAF=180°,
∵∠DAF=360°-60°-60°-90°=150°,
∴∠ADE=30°,∴AH=AD=3,
∴S平行四边形ADEF=DE×AH=12;
若AB=4,AC=6,
∵四边形ABCD是平行四边形,
∴DE∥AF,DE=AF=AC=6,AD=EF=AB=4,
∴∠ADE+∠DAF=180°,
∵∠DAF=360°-60°-60°-90°=150°,
∴∠ADE=30°,∴AH=AD=2,
∴S平行四边形ADEF=DE×AH=12;
综上:四边形ADEF的面积为12.
每日一题80 答案
80.【详解】解:(1)设运动时间为t秒.
∵四边形MNCB是平行四边形,∴MB=NC,
当N从D运动到C时,
∵BC=13cm,CD=21cm,∴BM=AB-AM=16-t,CN=21-2t,
∴16-t=21-2t,解得t=5,
当N从C运动到D时,∵BM=AB-AM=16-t,CN=2t-21
∴16-t=2t-21,解得t=,∴当t=5秒或秒时,四边形MNCB是平行四边形;
(2)△NMB是等腰三角形有三种情况,
Ⅰ.当NM=NB时,作NH⊥AB于H,则HM=HB,
当N从D运动到C时,∵MH=HB=BM=(16-t),
由AH=DN得2t=(16 t)+t,解得t=秒;
当点N从C向D运动时,观察图象可知,只有由题意:42-2t=(16-t)+t,
解得t=秒.
Ⅱ.当MN=MB,当N从D运动到C时,
MH=AH-AM=DN-AM=2t-t=t,BM=16-t,
∵MN2=t2+122,∴(16-t)2=122+t2,解得t=(秒);
Ⅲ.当BM=BN,当N从C运动到D时,
则BH=AB-AH=AB-DN=16-2t,
∵BM2=BN2=NH2+BH2=122+(16-2t)2,
∴(16-t)2=122+(16-2t)2,
即3t2-32t+144=0,
∵△<0,
∴方程无实根,
综上可知,当t=秒或秒或秒时,△BMN是等腰三角形.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
