八年级下每日一题91-95几何新定义问题之四边形(含解析)
文档属性
| 名称 | 八年级下每日一题91-95几何新定义问题之四边形(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-29 05:19:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
每日一题91 几何新定义问题之四边形
班级 姓名 学号
91.如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.
试证明:AB2+CD2=AD2+BC2;
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.
每日一题92 几何新定义问题之四边形
班级 姓名 学号
92.(2023·江苏中考)对于平面内的一个四边形,若存在点,使得该四边形的一条对角线绕点旋转一定角度后能与另一条对角线重合,则称该四边形为“可旋四边形”,点是该四边形的一个“旋点”.例如,在矩形中,对角线、相交于点,则点是矩形的一个“旋点”.
(1)若菱形为“可旋四边形”,其面积是,则菱形的边长是_______;
(2)如图1,四边形为“可旋四边形”,边的中点是四边形的一个“旋点”.求的度数;
(3)如图2,在四边形中,,与不平行.四边形是否为“可旋四边形”?请说明理由.
每日一题93 几何新定义问题之四边形
班级 姓名 学号
93.(2023·宁波·中考)定义:有两个相邻的内角是直角,并且有两条邻边相等的四边形称为邻等四边形,相等两邻边的夹角称为邻等角.
(1)如图1,在四边形中,,对角线平分.求证:四边形为邻等四边形.
(2)如图2,在6×5的方格纸中,A,B,C三点均在格点上,若四边形是邻等四边形,请画出所有符合条件的格点D.
(3)如图3,四边形是邻等四边形,,为邻等角,连接,过B作交的延长线于点E.若,求四边形的周长.
每日一题94 几何新定义问题之四边形
班级 姓名 学号
94.(2022·江苏常州中考)在四边形中,是边上的一点.若,则点叫做该四边形的“等形点”.
(1)正方形_______“等形点”(填“存在”或“不存在”);
(2)如图,在四边形中,边上的点是四边形的“等形点”.已知,,,连接,求的长;
(3)在四边形中,EH//FG.若边上的点是四边形的“等形点”,求的值.
每日一题95 几何新定义问题之四边形
班级 姓名 学号
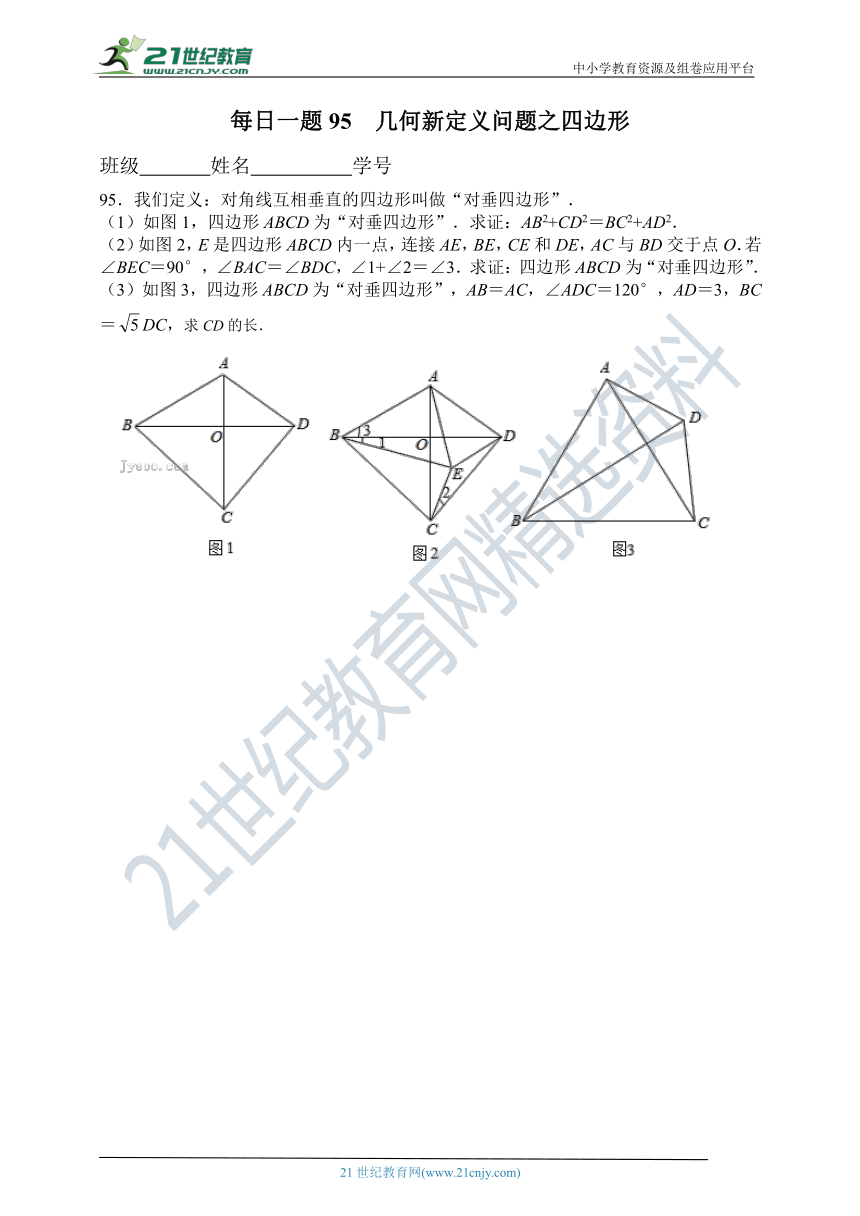
95.我们定义:对角线互相垂直的四边形叫做“对垂四边形”.
(1)如图1,四边形ABCD为“对垂四边形”.求证:AB2+CD2=BC2+AD2.
(2)如图2,E是四边形ABCD内一点,连接AE,BE,CE和DE,AC与BD交于点O.若∠BEC=90°,∠BAC=∠BDC,∠1+∠2=∠3.求证:四边形ABCD为“对垂四边形”.
(3)如图3,四边形ABCD为“对垂四边形”,AB=AC,∠ADC=120°,AD=3,BC=DC,求CD的长.
每日一题91 几何新定义问题 答案
解:(1)四边形ABCD是垂美四边形.
证明:∵AB=AD,∴点A在线段BD的垂直平分线上,
∵CB=CD,∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,∴AC⊥BD,即四边形ABCD是垂美四边形;
(2)猜想结论:垂美四边形的两组对边的平方和相等.
如图2,已知四边形ABCD中,AC⊥BD,垂足为E,
求证:AD2+BC2=AB2+CD2
证明:∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2; 故答案为:AD2+BC2=AB2+CD2.
(3)连接CG、BE,∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
又∵AG=AC,AB=AE,∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,∵AC=4,AB=5,∴BC=3,CG=4,BE=5,
∴GE2=CG2+BE2﹣CB2=73,∴GE=.
每日一题92 几何新定义问题 答案
【详解】(1)解:∵菱形为“可旋四边形”,
则菱形的一条对角线绕点旋转一定角度后能与另一条对角线重合,
即,则菱形为正方形,
∵菱形的面积为,
∴菱形的边长是.故答案为:.
(2)解:连接,如图:
∵四边形为“可旋四边形”,且点是四边形的一个“旋点”,
∴,∴,
∵点是边的中点,
∴,∴,∴,
∵,
即,∴.
(3)解:四边形是“可旋四边形”;理由如下:
分别作,的垂直平分线,交于点,连接,,,,如图:
∵点在线段和线段的垂直平分线上,
∴,,
在和中,
,
∴,
∴,
则,
即,
∴四边形是“可旋四边形”.
每日一题93 几何新定义问题 答案
93.(1)解:∵,
∴,,
∵对角线平分,
∴,
∴,
∴,
∴四边形为邻等四边形.
(2)解:,,即为所求;
(3)如图,过作于,
∵,
∴四边形是矩形,
∴,,
∵,
∴四边形为平行四边形,
∴,,
设,而,
∴,,
由新定义可得,
由勾股定理可得:,
整理得:,
解得:,(不符合题意舍去),
∴,
∴四边形的周长为.
每日一题94 几何新定义问题 答案
94.(1)不存在,
理由如下:假设正方形ABCD存在“等形点”点O,即存在△OAB≌△OCD,
∵在正方形ABCD中,点O在边BC上,∴∠ABO=90°,
∵△OAB≌△OCD,∴∠ABO=∠CDO=90°,∴CD⊥DO,
∵CD⊥BC,∴,
∵O点在BC上,∴DO与BC交于点O,∴假设不成立,
故正方形不存在“等形点”;
(2)如图,过A点作AM⊥BC于点M,如图,
∵O点是四边形ABCD的“等形点”,∴△OAB≌△OCD,
∴AB=CD,OA=OC,OB=OD,∠AOB=∠COD,
∵,OA=5,BC=12,∴AB=CD=,OA=OC=5,∴OB=BC-OC=12-5=7=OD,
∵AM⊥BC,∴∠AMO=90°=∠AMB,
∴设MO=a,则BM=BO-MO=7-a,
∴在Rt△ABM和Rt△AOM中,,
∴,即,
解得:,即,
∴MC=MO+OC=,
∴在Rt△AMC中,,
即AC的长为;
(3)如图,
∵O点是四边形EFGH的“等形点”,
∴△OEF≌△OGH,
∴OF=OH,OE=OG,∠EOF=∠GOH,
∵,
∴∠EOF=∠OEH,∠GOH=∠EHO,
∴根据∠EOF=∠GOH有∠OEH=∠OHE,
∴OE=OH,
∵OF=OH,OE=OG,
∴OF=OG,
∴.
每日一题95 几何新定义问题 答案
【解答】证明:(1)∵四边形ABCD为“对垂四边形”,
∴AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AB2+CD2=AD2+BC2;
(2)∵∠BAC=∠BDC,∠AOB=∠COD,
∴∠3=∠ACD,
∵∠3=∠1+∠2,∠ACD=∠ACE+∠2,
∴∠1=∠ACE,
∴∠BOC=∠BEC=90°,
∴AC⊥BD,
∴四边形ABCD为“对垂四边形”;
(3)过点A作AH⊥DC,交CD延长线于点H,
设CD=x,则BC=DC=x,
∵四边形ABCD为“对垂四边形”,AD=3,
∴AB2+CD2=AD2+BC2,
∴AB2=9+5x2﹣x2=9+4x2,
∵AB=AC,
∴AC2=9+4x2,
∵∠ADC=120°,
∴∠ADH=60°,∠DAH=30°,
∴DH=AD=,AH=DH=,
∵AC2=AH2+CH2,
∴9+4x2=+(x+)2,
∴x1=0(舍去),x2=1,
∴CD的长度1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
每日一题91 几何新定义问题之四边形
班级 姓名 学号
91.如图1,对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;
(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.
试证明:AB2+CD2=AD2+BC2;
(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.
每日一题92 几何新定义问题之四边形
班级 姓名 学号
92.(2023·江苏中考)对于平面内的一个四边形,若存在点,使得该四边形的一条对角线绕点旋转一定角度后能与另一条对角线重合,则称该四边形为“可旋四边形”,点是该四边形的一个“旋点”.例如,在矩形中,对角线、相交于点,则点是矩形的一个“旋点”.
(1)若菱形为“可旋四边形”,其面积是,则菱形的边长是_______;
(2)如图1,四边形为“可旋四边形”,边的中点是四边形的一个“旋点”.求的度数;
(3)如图2,在四边形中,,与不平行.四边形是否为“可旋四边形”?请说明理由.
每日一题93 几何新定义问题之四边形
班级 姓名 学号
93.(2023·宁波·中考)定义:有两个相邻的内角是直角,并且有两条邻边相等的四边形称为邻等四边形,相等两邻边的夹角称为邻等角.
(1)如图1,在四边形中,,对角线平分.求证:四边形为邻等四边形.
(2)如图2,在6×5的方格纸中,A,B,C三点均在格点上,若四边形是邻等四边形,请画出所有符合条件的格点D.
(3)如图3,四边形是邻等四边形,,为邻等角,连接,过B作交的延长线于点E.若,求四边形的周长.
每日一题94 几何新定义问题之四边形
班级 姓名 学号
94.(2022·江苏常州中考)在四边形中,是边上的一点.若,则点叫做该四边形的“等形点”.
(1)正方形_______“等形点”(填“存在”或“不存在”);
(2)如图,在四边形中,边上的点是四边形的“等形点”.已知,,,连接,求的长;
(3)在四边形中,EH//FG.若边上的点是四边形的“等形点”,求的值.
每日一题95 几何新定义问题之四边形
班级 姓名 学号
95.我们定义:对角线互相垂直的四边形叫做“对垂四边形”.
(1)如图1,四边形ABCD为“对垂四边形”.求证:AB2+CD2=BC2+AD2.
(2)如图2,E是四边形ABCD内一点,连接AE,BE,CE和DE,AC与BD交于点O.若∠BEC=90°,∠BAC=∠BDC,∠1+∠2=∠3.求证:四边形ABCD为“对垂四边形”.
(3)如图3,四边形ABCD为“对垂四边形”,AB=AC,∠ADC=120°,AD=3,BC=DC,求CD的长.
每日一题91 几何新定义问题 答案
解:(1)四边形ABCD是垂美四边形.
证明:∵AB=AD,∴点A在线段BD的垂直平分线上,
∵CB=CD,∴点C在线段BD的垂直平分线上,
∴直线AC是线段BD的垂直平分线,∴AC⊥BD,即四边形ABCD是垂美四边形;
(2)猜想结论:垂美四边形的两组对边的平方和相等.
如图2,已知四边形ABCD中,AC⊥BD,垂足为E,
求证:AD2+BC2=AB2+CD2
证明:∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,
由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,
∴AD2+BC2=AB2+CD2; 故答案为:AD2+BC2=AB2+CD2.
(3)连接CG、BE,∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
又∵AG=AC,AB=AE,∴△GAB≌△CAE(SAS),
∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,
∴四边形CGEB是垂美四边形,
由(2)得,CG2+BE2=CB2+GE2,∵AC=4,AB=5,∴BC=3,CG=4,BE=5,
∴GE2=CG2+BE2﹣CB2=73,∴GE=.
每日一题92 几何新定义问题 答案
【详解】(1)解:∵菱形为“可旋四边形”,
则菱形的一条对角线绕点旋转一定角度后能与另一条对角线重合,
即,则菱形为正方形,
∵菱形的面积为,
∴菱形的边长是.故答案为:.
(2)解:连接,如图:
∵四边形为“可旋四边形”,且点是四边形的一个“旋点”,
∴,∴,
∵点是边的中点,
∴,∴,∴,
∵,
即,∴.
(3)解:四边形是“可旋四边形”;理由如下:
分别作,的垂直平分线,交于点,连接,,,,如图:
∵点在线段和线段的垂直平分线上,
∴,,
在和中,
,
∴,
∴,
则,
即,
∴四边形是“可旋四边形”.
每日一题93 几何新定义问题 答案
93.(1)解:∵,
∴,,
∵对角线平分,
∴,
∴,
∴,
∴四边形为邻等四边形.
(2)解:,,即为所求;
(3)如图,过作于,
∵,
∴四边形是矩形,
∴,,
∵,
∴四边形为平行四边形,
∴,,
设,而,
∴,,
由新定义可得,
由勾股定理可得:,
整理得:,
解得:,(不符合题意舍去),
∴,
∴四边形的周长为.
每日一题94 几何新定义问题 答案
94.(1)不存在,
理由如下:假设正方形ABCD存在“等形点”点O,即存在△OAB≌△OCD,
∵在正方形ABCD中,点O在边BC上,∴∠ABO=90°,
∵△OAB≌△OCD,∴∠ABO=∠CDO=90°,∴CD⊥DO,
∵CD⊥BC,∴,
∵O点在BC上,∴DO与BC交于点O,∴假设不成立,
故正方形不存在“等形点”;
(2)如图,过A点作AM⊥BC于点M,如图,
∵O点是四边形ABCD的“等形点”,∴△OAB≌△OCD,
∴AB=CD,OA=OC,OB=OD,∠AOB=∠COD,
∵,OA=5,BC=12,∴AB=CD=,OA=OC=5,∴OB=BC-OC=12-5=7=OD,
∵AM⊥BC,∴∠AMO=90°=∠AMB,
∴设MO=a,则BM=BO-MO=7-a,
∴在Rt△ABM和Rt△AOM中,,
∴,即,
解得:,即,
∴MC=MO+OC=,
∴在Rt△AMC中,,
即AC的长为;
(3)如图,
∵O点是四边形EFGH的“等形点”,
∴△OEF≌△OGH,
∴OF=OH,OE=OG,∠EOF=∠GOH,
∵,
∴∠EOF=∠OEH,∠GOH=∠EHO,
∴根据∠EOF=∠GOH有∠OEH=∠OHE,
∴OE=OH,
∵OF=OH,OE=OG,
∴OF=OG,
∴.
每日一题95 几何新定义问题 答案
【解答】证明:(1)∵四边形ABCD为“对垂四边形”,
∴AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°,
由勾股定理得,AD2+BC2=AO2+DO2+BO2+CO2,
AB2+CD2=AO2+BO2+CO2+DO2,
∴AB2+CD2=AD2+BC2;
(2)∵∠BAC=∠BDC,∠AOB=∠COD,
∴∠3=∠ACD,
∵∠3=∠1+∠2,∠ACD=∠ACE+∠2,
∴∠1=∠ACE,
∴∠BOC=∠BEC=90°,
∴AC⊥BD,
∴四边形ABCD为“对垂四边形”;
(3)过点A作AH⊥DC,交CD延长线于点H,
设CD=x,则BC=DC=x,
∵四边形ABCD为“对垂四边形”,AD=3,
∴AB2+CD2=AD2+BC2,
∴AB2=9+5x2﹣x2=9+4x2,
∵AB=AC,
∴AC2=9+4x2,
∵∠ADC=120°,
∴∠ADH=60°,∠DAH=30°,
∴DH=AD=,AH=DH=,
∵AC2=AH2+CH2,
∴9+4x2=+(x+)2,
∴x1=0(舍去),x2=1,
∴CD的长度1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
