【浙教版八上同步练习】 第四章 图形与坐标检测题(培优)(含答案)
文档属性
| 名称 | 【浙教版八上同步练习】 第四章 图形与坐标检测题(培优)(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-28 15:10:37 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【浙教版八上同步练习】
第四章图形与坐标检测题(培优)
一、单选题
1.下列各组数中,不相等的一组是( )
A.(﹣3)2与﹣32 B.﹣|﹣3|2与﹣32
C.﹣|﹣3|3与﹣33 D.(﹣3)3 与﹣33
2.在平面直角坐标系中,点A的坐标为(-7,3),点B的坐标为(3,3),则线段AB的位置特征为( )
A.与x轴平行 B.与y轴平行
C.在第一、三象限的角平分线上 D.在第二、四象限的角平分线上
3.平面内点A(﹣1,2)和点B(﹣1,﹣2)的对称轴是( )
A.x轴 B.y轴 C.直线y=4 D.直线x=﹣1
4.若在象棋盘上建立直角坐标系,使“帥”位于点(-1,-2),“馬”位于点(2,-2),则“兵”位于点
A.(-1,1) B.(-2,-1)
C.(-3,1) D.(1,-2)
5.已知A,B,C,D四位同学的家所在位置如图所示,若以A同学家的位置为坐标原点建立平面直角坐标系,C同学家的坐标为(1,5),则B,D两同学家的坐标分别为( )
A.(2,3),(3,2) B.(3,2),(2,3)
C.(2,3),(-3,2) D.(3,2),(-2,3)
二、填空题
6.定义:在平面直角坐标系中,对于任意两点,如果点满足:,那么称点M是点A,B的“双减点”.
(i)若点,的“双减点”M的坐标是,则点B的坐标是 ;
(ii)若点,的“双减点”是点F,当点F在直线的上方时,则m的取值范围是 .
7.观察中国象棋的棋盘,其中“马”的位置可以用一个数对(3,5)来表示,则表示“兵”点位置的数对是 .
8.在平面直角坐标系中,已知线段 轴,点A的坐标是 且 ,则点B的坐标是 .
9.如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°,点M′的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为 .
10.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为300m,且桥宽忽略不计,则小桥总长为 m.
三、解答题
11.如图的方格中有25个汉字,如四1表示“天”,请沿着以下路径去寻找你的礼物:
(1)一1→三2→二4→四3→五1
一 二 三 四 五
1 我 力 习 天 的
2 会 上 是 学 好
3 帅 就 更 棒 努
4 优 最 行 了 可
5 能 爱 秀 明 哥
(2)五3→二1→二3→一5→三4
(3)四5→四1→一2→三3→五2.
12.如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1,并写出点A1、B1、C1的坐标。
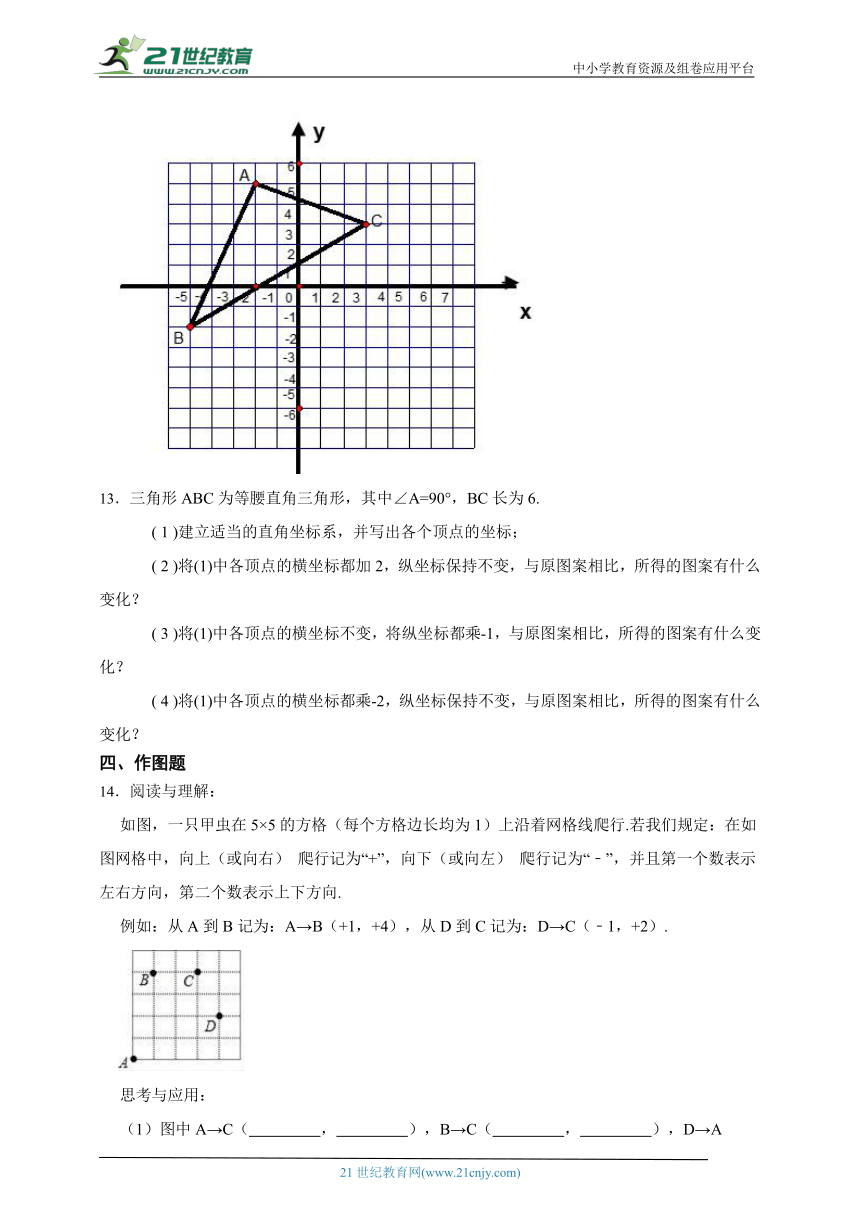
13.三角形ABC为等腰直角三角形,其中∠A=90°,BC长为6.
( 1 )建立适当的直角坐标系,并写出各个顶点的坐标;
( 2 )将(1)中各顶点的横坐标都加2,纵坐标保持不变,与原图案相比,所得的图案有什么变化?
( 3 )将(1)中各顶点的横坐标不变,将纵坐标都乘-1,与原图案相比,所得的图案有什么变化?
( 4 )将(1)中各顶点的横坐标都乘-2,纵坐标保持不变,与原图案相比,所得的图案有什么变化?
四、作图题
14.阅读与理解:
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右) 爬行记为“+”,向下(或向左) 爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中A→C( , ),B→C( , ),D→A( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程.
五、综合题
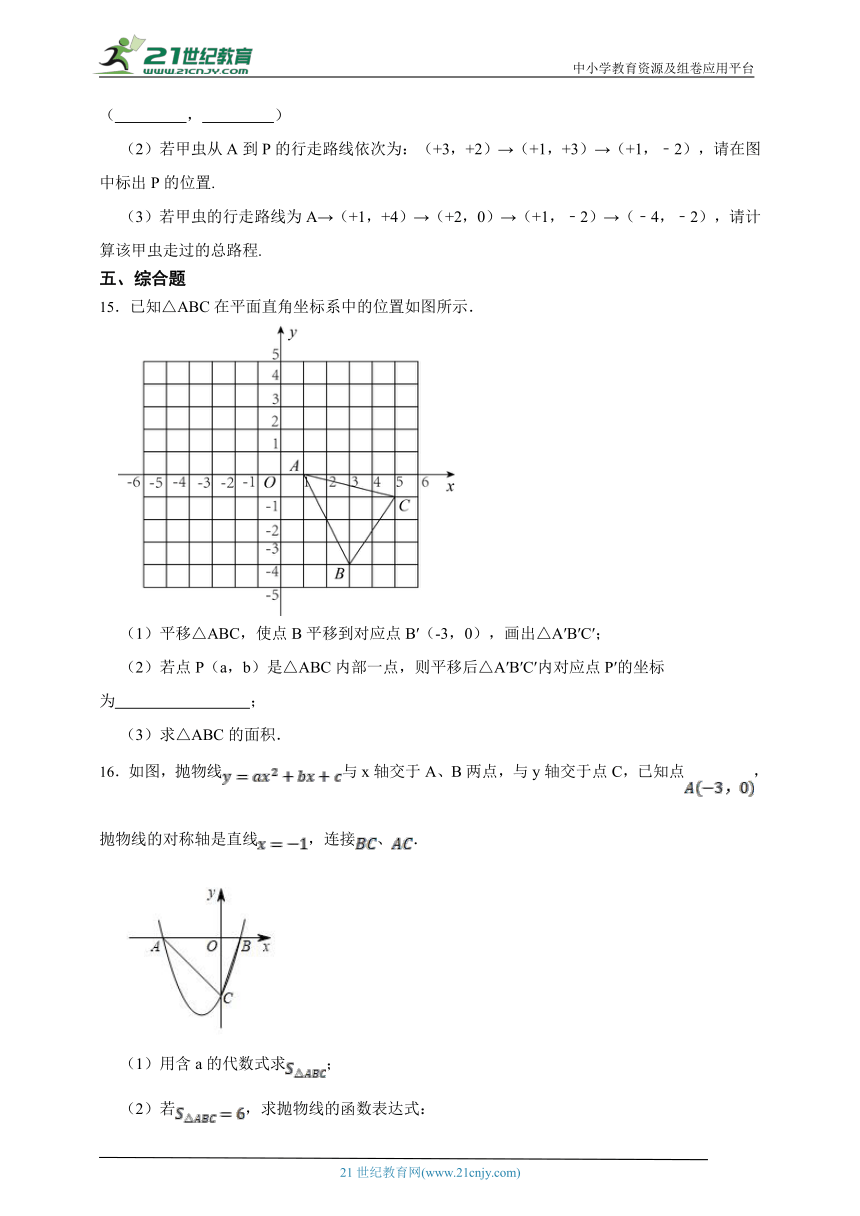
15.已知△ABC在平面直角坐标系中的位置如图所示.
(1)平移△ABC,使点B平移到对应点B′(-3,0),画出△A′B′C′;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内对应点P′的坐标为 ;
(3)求△ABC的面积.
16.如图,抛物线与x轴交于A、B两点,与y轴交于点C,已知点,抛物线的对称轴是直线,连接、.
(1)用含a的代数式求;
(2)若,求抛物线的函数表达式:
(3)在(2)的条件下,当时,y的最小值是-2,求m的值.
17.将一张矩形的纸片放到平面直角坐标系中,使矩形OABC的两边OA、OC分别落在x轴、y轴上.如图,将△OAB沿对角线OB翻折到△ONB,ON与CB交于点M.
(1)重叠部分△OBM是什么形状的三角形,请说明你的理由;
(2)已知OC=3,,请直接写出点M坐标( , ).
六、实践探究题
18.综合与实践
(1)【动手实验】数学课上,老师带领同学们对角的平分线的性质进行探究:
同学们任意作一个,作出的平分线在上任取一点,过点画出,的垂线,分别记垂足为,,测量,第一小组的测量结果如下:
学生 学生
小明 小刚
小红 小丽
通过以上测量,你发现了角的平分线的什么性质?
(2)【推理证明】请结合图,利用三角形全等证明这个性质.
如图1,已知:,点在上,,,垂足分别为,求证:.
(3)【定理应用】如图2,点是的角平分线上一点,,垂足为点,且,点是射线上一动点,求的最小值.
答案解析部分
1.【答案】A
【知识点】绝对值及有理数的绝对值;有理数大小比较;有理数的乘方法则
2.【答案】A
【知识点】点的坐标
3.【答案】A
【知识点】关于坐标轴对称的点的坐标特征
4.【答案】C
【知识点】用坐标表示地理位置
5.【答案】D
【知识点】点的坐标;平面直角坐标系的构成
6.【答案】(-5,10);
【知识点】点的坐标;一次函数与不等式(组)的综合应用
7.【答案】(6,7)
【知识点】用坐标表示地理位置
8.【答案】(2,3)或( 6,3)
【知识点】点的坐标;坐标与图形变化﹣平移
9.【答案】(﹣3,5)
【知识点】点的坐标;平行线的性质;含30°角的直角三角形;三角形全等的判定(AAS)
10.【答案】150
【知识点】矩形的性质;平移的性质
11.【答案】解:(1)一1表示我,三2表示是,二4表示最,四3表示棒,五1表示的,
所以礼物为:我是最棒的;
(2)五3表示努,二1表示力,二3表示就,一5表示能,三4行,
所以礼物为:努力就能行;
(3)四5表示明,四1表示天,一2表示会,三3表示更,五2表示好,
所以礼物为:明天会更好.
【知识点】用坐标表示地理位置
12.【答案】作图:
A1(0,2)B1(-3,-5)C1(5,0)
【知识点】用坐标表示平移
13.【答案】解:( 1 )以BC边所在的直线为x轴,BC的中垂线(垂足为O)为y轴,建立直角坐标系(如图).因为BC的长为6,所以AO=BC=3,所以A(0,3),B(-3,0),C(3,0)
( 2 )整个图案向右平移了2个单位长度,如图△A2B2C2;
( 3 )与原图案关于x轴对称,如图△A3BC;
( 4 )与原图形相比所得的图案在位置上关于y轴对称,横向拉长了2倍,如图△AB4C4.
【知识点】坐标与图形变化﹣对称;坐标与图形变化﹣平移
14.【答案】(1)+3;+4;+2;0;﹣4;﹣2
(2)解:如图2所示.
(3)解:甲虫走过的总路程:
|+1|+|+4|+|+2|+|+1|+|﹣2|+|﹣4|+|﹣2|=16.
【知识点】坐标与图形变化﹣平移
15.【答案】(1)解:解:∵点B的坐标是(3,-4),将点B左移6个单位,上移4个单位顶点点B′(-3,0),
∴点A的坐标是(1,0),将点A左移6个单位,上移4个单位顶点点A'(-5,4);
点C的坐标是(5,-1),将点C左移6个单位,上移4个单位顶点点C'(-1,3),
顺次连接A'B'、B'C'、C' A'得到△A'B'C',如图,△A'B'C'即为所求;
(2)(a-6,b+4)
(3)解:S△ABC=4×4-2×4-2×3-1×4=7
【知识点】三角形的面积;坐标与图形变化﹣平移;作图﹣平移
16.【答案】(1)解:将点A的坐标代入抛物线表达式得:9a-3b+c=0①,
∵函数的对称轴为:,
∴b=2a②,
将②代入①得c=-3a,
∴抛物线的表达式为:y=ax2+2ax-3a,
设y=ax2+2ax-3a=0,
解得x=1或-3,
∴B的坐标为(1,0),
∴AB=1-(-3)=4,
∵图象的开口向上,
∴a>0,
当x=0时,y=-3a,
∴C(0,-3a),
∴OC=3a,
∴ ;
(2)解:∵,
∴a=1,
∴抛物线的表达式为:y=x2+2x-3;
(3)解:①当m-1≥-1时,即m>0,
函数在x= m-1 时,取得最小值,
即 ,
解得 (负值舍去),
∴;
②当m-1<-1时,即m<0,
当x=-1时,函数取得最小值,
而顶点的纵坐标,
故此时,不存在m的值,使得y的最小值是-2;
综上所述,.
【知识点】三角形的面积;二次函数y=ax^2+bx+c的性质
17.【答案】(1)解:△OBM是等腰三角形,理由如下,∵四边形OABC是矩形,∴OA∥BC,∴∠AOB=∠OBC,由折叠得∠AOB=∠BON,∴∠OBC=∠BON,∴OM=BM,∴△OBM是等腰三角形;
(2)1;3
【知识点】点的坐标;勾股定理;翻折变换(折叠问题)
18.【答案】(1)解:发现:角的平分线上的点到角的两边的距离相等;
(2)证明:,,
,
在和中,
,
≌,
;
(3)解:当时,最小,
,为的角平分线,
,
的最小值为3.
【知识点】垂线段最短;角平分线的性质;三角形全等的判定(AAS)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【浙教版八上同步练习】
第四章图形与坐标检测题(培优)
一、单选题
1.下列各组数中,不相等的一组是( )
A.(﹣3)2与﹣32 B.﹣|﹣3|2与﹣32
C.﹣|﹣3|3与﹣33 D.(﹣3)3 与﹣33
2.在平面直角坐标系中,点A的坐标为(-7,3),点B的坐标为(3,3),则线段AB的位置特征为( )
A.与x轴平行 B.与y轴平行
C.在第一、三象限的角平分线上 D.在第二、四象限的角平分线上
3.平面内点A(﹣1,2)和点B(﹣1,﹣2)的对称轴是( )
A.x轴 B.y轴 C.直线y=4 D.直线x=﹣1
4.若在象棋盘上建立直角坐标系,使“帥”位于点(-1,-2),“馬”位于点(2,-2),则“兵”位于点
A.(-1,1) B.(-2,-1)
C.(-3,1) D.(1,-2)
5.已知A,B,C,D四位同学的家所在位置如图所示,若以A同学家的位置为坐标原点建立平面直角坐标系,C同学家的坐标为(1,5),则B,D两同学家的坐标分别为( )
A.(2,3),(3,2) B.(3,2),(2,3)
C.(2,3),(-3,2) D.(3,2),(-2,3)
二、填空题
6.定义:在平面直角坐标系中,对于任意两点,如果点满足:,那么称点M是点A,B的“双减点”.
(i)若点,的“双减点”M的坐标是,则点B的坐标是 ;
(ii)若点,的“双减点”是点F,当点F在直线的上方时,则m的取值范围是 .
7.观察中国象棋的棋盘,其中“马”的位置可以用一个数对(3,5)来表示,则表示“兵”点位置的数对是 .
8.在平面直角坐标系中,已知线段 轴,点A的坐标是 且 ,则点B的坐标是 .
9.如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°,点M′的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为 .
10.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的长方形荷塘上架设小桥.若荷塘周长为300m,且桥宽忽略不计,则小桥总长为 m.
三、解答题
11.如图的方格中有25个汉字,如四1表示“天”,请沿着以下路径去寻找你的礼物:
(1)一1→三2→二4→四3→五1
一 二 三 四 五
1 我 力 习 天 的
2 会 上 是 学 好
3 帅 就 更 棒 努
4 优 最 行 了 可
5 能 爱 秀 明 哥
(2)五3→二1→二3→一5→三4
(3)四5→四1→一2→三3→五2.
12.如图,将三角形ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的三角形A1B1C1,并写出点A1、B1、C1的坐标。
13.三角形ABC为等腰直角三角形,其中∠A=90°,BC长为6.
( 1 )建立适当的直角坐标系,并写出各个顶点的坐标;
( 2 )将(1)中各顶点的横坐标都加2,纵坐标保持不变,与原图案相比,所得的图案有什么变化?
( 3 )将(1)中各顶点的横坐标不变,将纵坐标都乘-1,与原图案相比,所得的图案有什么变化?
( 4 )将(1)中各顶点的横坐标都乘-2,纵坐标保持不变,与原图案相比,所得的图案有什么变化?
四、作图题
14.阅读与理解:
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右) 爬行记为“+”,向下(或向左) 爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中A→C( , ),B→C( , ),D→A( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程.
五、综合题
15.已知△ABC在平面直角坐标系中的位置如图所示.
(1)平移△ABC,使点B平移到对应点B′(-3,0),画出△A′B′C′;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内对应点P′的坐标为 ;
(3)求△ABC的面积.
16.如图,抛物线与x轴交于A、B两点,与y轴交于点C,已知点,抛物线的对称轴是直线,连接、.
(1)用含a的代数式求;
(2)若,求抛物线的函数表达式:
(3)在(2)的条件下,当时,y的最小值是-2,求m的值.
17.将一张矩形的纸片放到平面直角坐标系中,使矩形OABC的两边OA、OC分别落在x轴、y轴上.如图,将△OAB沿对角线OB翻折到△ONB,ON与CB交于点M.
(1)重叠部分△OBM是什么形状的三角形,请说明你的理由;
(2)已知OC=3,,请直接写出点M坐标( , ).
六、实践探究题
18.综合与实践
(1)【动手实验】数学课上,老师带领同学们对角的平分线的性质进行探究:
同学们任意作一个,作出的平分线在上任取一点,过点画出,的垂线,分别记垂足为,,测量,第一小组的测量结果如下:
学生 学生
小明 小刚
小红 小丽
通过以上测量,你发现了角的平分线的什么性质?
(2)【推理证明】请结合图,利用三角形全等证明这个性质.
如图1,已知:,点在上,,,垂足分别为,求证:.
(3)【定理应用】如图2,点是的角平分线上一点,,垂足为点,且,点是射线上一动点,求的最小值.
答案解析部分
1.【答案】A
【知识点】绝对值及有理数的绝对值;有理数大小比较;有理数的乘方法则
2.【答案】A
【知识点】点的坐标
3.【答案】A
【知识点】关于坐标轴对称的点的坐标特征
4.【答案】C
【知识点】用坐标表示地理位置
5.【答案】D
【知识点】点的坐标;平面直角坐标系的构成
6.【答案】(-5,10);
【知识点】点的坐标;一次函数与不等式(组)的综合应用
7.【答案】(6,7)
【知识点】用坐标表示地理位置
8.【答案】(2,3)或( 6,3)
【知识点】点的坐标;坐标与图形变化﹣平移
9.【答案】(﹣3,5)
【知识点】点的坐标;平行线的性质;含30°角的直角三角形;三角形全等的判定(AAS)
10.【答案】150
【知识点】矩形的性质;平移的性质
11.【答案】解:(1)一1表示我,三2表示是,二4表示最,四3表示棒,五1表示的,
所以礼物为:我是最棒的;
(2)五3表示努,二1表示力,二3表示就,一5表示能,三4行,
所以礼物为:努力就能行;
(3)四5表示明,四1表示天,一2表示会,三3表示更,五2表示好,
所以礼物为:明天会更好.
【知识点】用坐标表示地理位置
12.【答案】作图:
A1(0,2)B1(-3,-5)C1(5,0)
【知识点】用坐标表示平移
13.【答案】解:( 1 )以BC边所在的直线为x轴,BC的中垂线(垂足为O)为y轴,建立直角坐标系(如图).因为BC的长为6,所以AO=BC=3,所以A(0,3),B(-3,0),C(3,0)
( 2 )整个图案向右平移了2个单位长度,如图△A2B2C2;
( 3 )与原图案关于x轴对称,如图△A3BC;
( 4 )与原图形相比所得的图案在位置上关于y轴对称,横向拉长了2倍,如图△AB4C4.
【知识点】坐标与图形变化﹣对称;坐标与图形变化﹣平移
14.【答案】(1)+3;+4;+2;0;﹣4;﹣2
(2)解:如图2所示.
(3)解:甲虫走过的总路程:
|+1|+|+4|+|+2|+|+1|+|﹣2|+|﹣4|+|﹣2|=16.
【知识点】坐标与图形变化﹣平移
15.【答案】(1)解:解:∵点B的坐标是(3,-4),将点B左移6个单位,上移4个单位顶点点B′(-3,0),
∴点A的坐标是(1,0),将点A左移6个单位,上移4个单位顶点点A'(-5,4);
点C的坐标是(5,-1),将点C左移6个单位,上移4个单位顶点点C'(-1,3),
顺次连接A'B'、B'C'、C' A'得到△A'B'C',如图,△A'B'C'即为所求;
(2)(a-6,b+4)
(3)解:S△ABC=4×4-2×4-2×3-1×4=7
【知识点】三角形的面积;坐标与图形变化﹣平移;作图﹣平移
16.【答案】(1)解:将点A的坐标代入抛物线表达式得:9a-3b+c=0①,
∵函数的对称轴为:,
∴b=2a②,
将②代入①得c=-3a,
∴抛物线的表达式为:y=ax2+2ax-3a,
设y=ax2+2ax-3a=0,
解得x=1或-3,
∴B的坐标为(1,0),
∴AB=1-(-3)=4,
∵图象的开口向上,
∴a>0,
当x=0时,y=-3a,
∴C(0,-3a),
∴OC=3a,
∴ ;
(2)解:∵,
∴a=1,
∴抛物线的表达式为:y=x2+2x-3;
(3)解:①当m-1≥-1时,即m>0,
函数在x= m-1 时,取得最小值,
即 ,
解得 (负值舍去),
∴;
②当m-1<-1时,即m<0,
当x=-1时,函数取得最小值,
而顶点的纵坐标,
故此时,不存在m的值,使得y的最小值是-2;
综上所述,.
【知识点】三角形的面积;二次函数y=ax^2+bx+c的性质
17.【答案】(1)解:△OBM是等腰三角形,理由如下,∵四边形OABC是矩形,∴OA∥BC,∴∠AOB=∠OBC,由折叠得∠AOB=∠BON,∴∠OBC=∠BON,∴OM=BM,∴△OBM是等腰三角形;
(2)1;3
【知识点】点的坐标;勾股定理;翻折变换(折叠问题)
18.【答案】(1)解:发现:角的平分线上的点到角的两边的距离相等;
(2)证明:,,
,
在和中,
,
≌,
;
(3)解:当时,最小,
,为的角平分线,
,
的最小值为3.
【知识点】垂线段最短;角平分线的性质;三角形全等的判定(AAS)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
