【浙教版八上同步练习】 第五章 一次函数检测题(培优)(含答案)
文档属性
| 名称 | 【浙教版八上同步练习】 第五章 一次函数检测题(培优)(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 9.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-29 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【浙教版八上同步练习】
第五章一次函数检测题(培优)
一、单选题
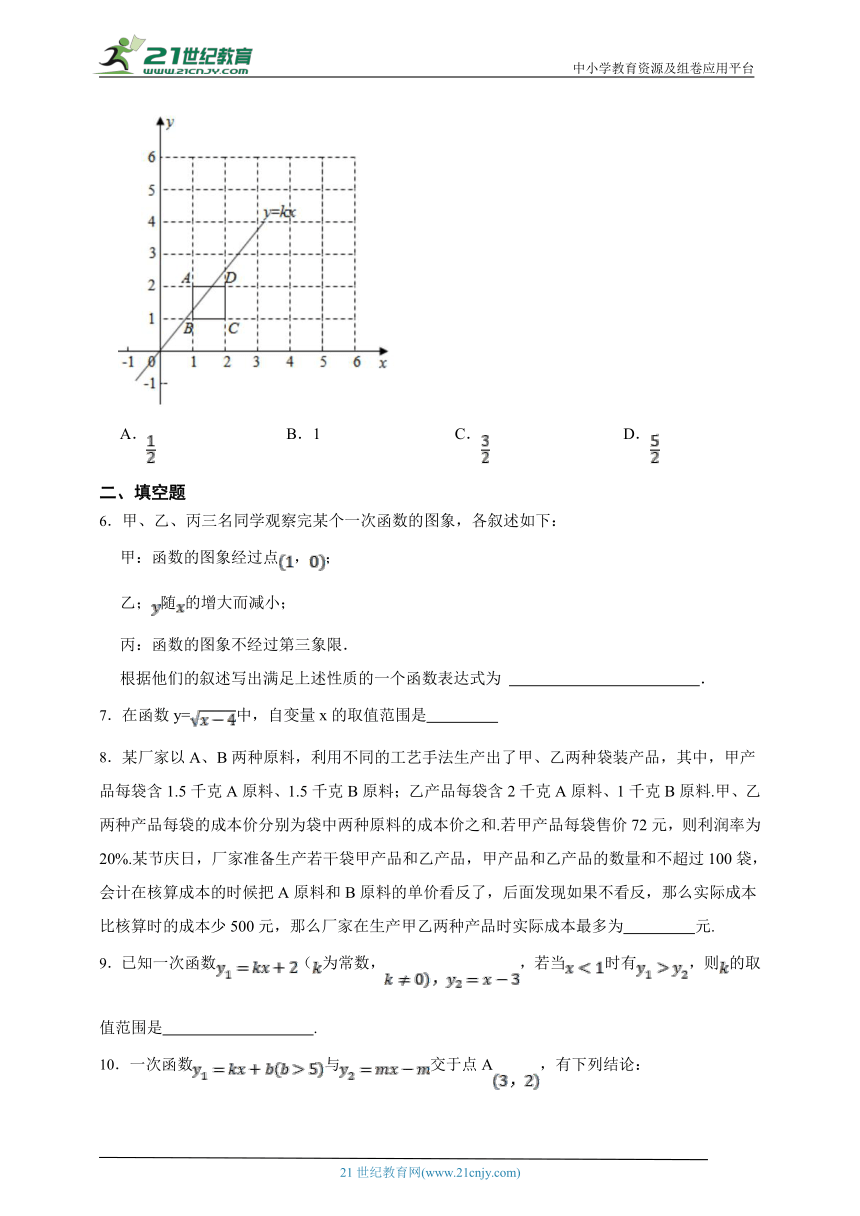
1.若方程ax+b=0的解是x=﹣2,则图中一定不是直线y=ax+b的是( )
A. B.
C. D.
2.直线y=kx+b交坐标轴于A(﹣8,0),B(0,13)两点,则不等式kx+b≥0的解集为( )
A.x≥﹣8 B.x≤﹣8 C.x≥13 D.x≤13
3.如图(1),四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图(2)所示,当P运动到BC中点时,△APD的面积为( )
A.4 B.5 C.6 D.7
4.已知直线y=kx+b经过第一、二、四象限,那么直线y=bx+k一定不经过( )
A.第一象限; B.第二象限; C.第三象限; D.第四象限.
5.将 的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是 ,正方形 的顶点都在格点上,若直线 与正方形 有公共点,则 的值不可能是( )
A. B.1 C. D.
二、填空题
6.甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
甲:函数的图象经过点,;
乙;随的增大而减小;
丙:函数的图象不经过第三象限.
根据他们的叙述写出满足上述性质的一个函数表达式为 .
7.在函数y=中,自变量x的取值范围是
8.某厂家以A、B两种原料,利用不同的工艺手法生产出了甲、乙两种袋装产品,其中,甲产品每袋含1.5千克A原料、1.5千克B原料;乙产品每袋含2千克A原料、1千克B原料.甲、乙两种产品每袋的成本价分别为袋中两种原料的成本价之和.若甲产品每袋售价72元,则利润率为20%.某节庆日,厂家准备生产若干袋甲产品和乙产品,甲产品和乙产品的数量和不超过100袋,会计在核算成本的时候把A原料和B原料的单价看反了,后面发现如果不看反,那么实际成本比核算时的成本少500元,那么厂家在生产甲乙两种产品时实际成本最多为 元.
9.已知一次函数(为常数,,若当时有,则的取值范围是 .
10.一次函数与交于点A,有下列结论:
①关于x的方程的解为;
②关于x的不等式组的解集为;
③;
④若,则或
其中正确的结论是 .(填写序号)
三、计算题
11.已知y与x成正比例关系,当时,,求:当时y的值.
12.周老师为锻炼身体一直坚持步行上下班.已知学校到周老师家总路程为2000米.一天,周老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.周老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.
(1)求a的值.
(2)b= ;c= .
(3)求周老师从学校到家的平均速度.
四、解答题
13.已知 与 成正比例,且 时, .求 关于 的函数表达式;
14.如图,直线AB:y=x+1与直线CD:y=﹣2x+4交于点E.
(1)求E点坐标;
(2)在x轴上找一点F使得FB+FE最小,求OF的长;
(3)若P为直线CD上一点,当△AEP面积为6时,求P的坐标.
五、作图题
15.甲乙两位老师同住一小区,该小区与学校相距2000米.甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为170米/分,甲步行的速度比乙步行的速度每分钟快5米.设甲步行的时间为 (分),图1中线段 与折线 分别表示甲、乙离小区的路程 (米)与甲步行时间 (分)的函数关系的图象;图2表示甲、乙两人之间的距离 (米)与甲步行时间 (分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求直线 的解析式;
(3)在图2中,画出当 时, 关于 的函数的大致图象.
六、综合题
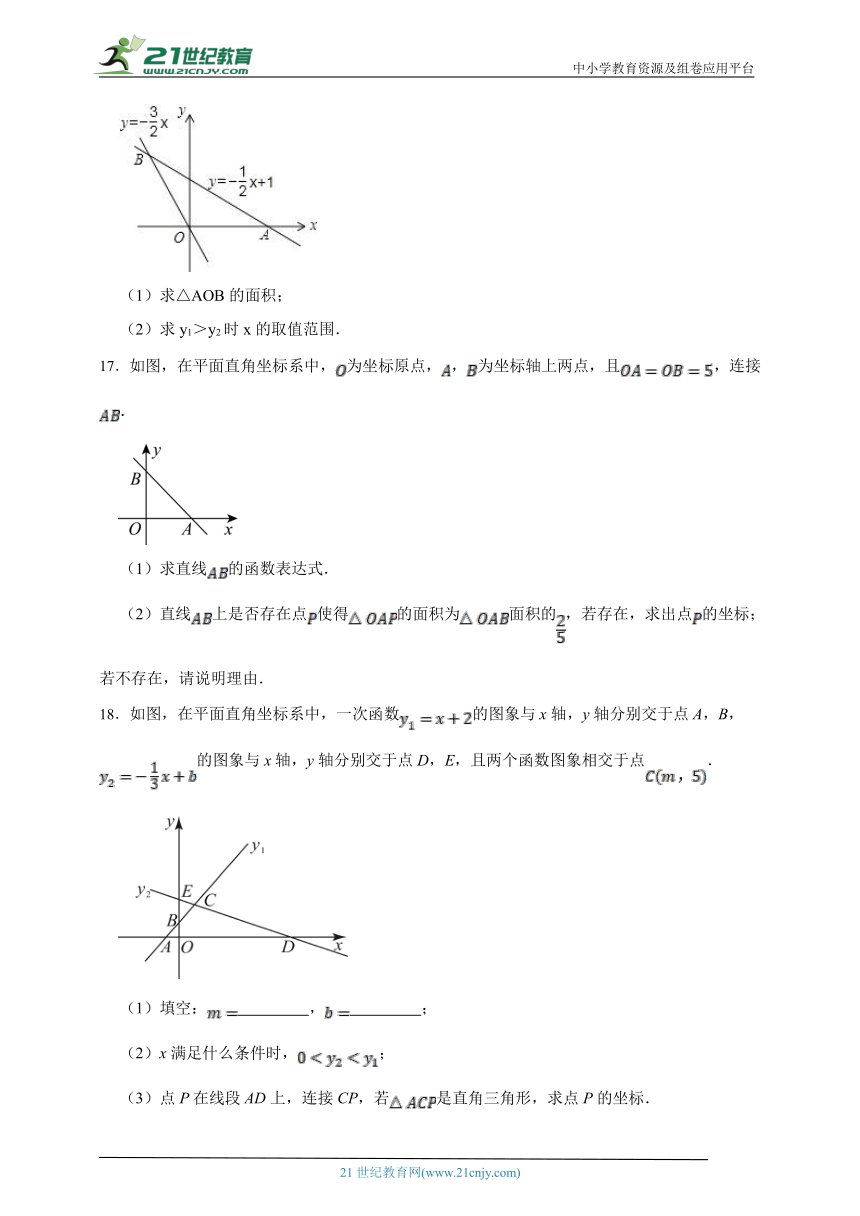
16.如图,已知直线y1=﹣ x+1与x轴交于点A,与直线y2=﹣ x交于点B.
(1)求△AOB的面积;
(2)求y1>y2时x的取值范围.
17.如图,在平面直角坐标系中,为坐标原点,,为坐标轴上两点,且,连接.
(1)求直线的函数表达式.
(2)直线上是否存在点使得的面积为面积的,若存在,求出点的坐标;若不存在,请说明理由.
18.如图,在平面直角坐标系中,一次函数的图象与x轴,y轴分别交于点A,B,的图象与x轴,y轴分别交于点D,E,且两个函数图象相交于点.
(1)填空: , ;
(2)x满足什么条件时,;
(3)点P在线段AD上,连接CP,若是直角三角形,求点P的坐标.
19.在平面直角坐标系中, 为坐标原点直线 与 轴交于点 ,与 轴交于点 , , 的面积为2.
(1)如图1,求直线 的解析式;
(2)如图2,线段 上有一点 ,直线 为 , 轴,将 绕点 顺时针旋转 ,交 于点 ,求点 的坐标.(用含 的式子表示)
(3)如图3,在(2)的条件下,连接 ,交直线 于点 ,若 ,求点 的坐标.
答案解析部分
1.【答案】B
【知识点】一次函数与一元一次方程的综合应用
2.【答案】A
【知识点】一次函数与不等式(组)的综合应用
3.【答案】B
【知识点】通过函数图象获取信息并解决问题
4.【答案】B
【知识点】两一次函数图象相交或平行问题;一次函数图象与坐标轴交点问题
5.【答案】D
【知识点】一次函数图象、性质与系数的关系
6.【答案】(答案不唯一)
【知识点】列一次函数关系式;一次函数图象、性质与系数的关系
7.【答案】x≥4
【知识点】函数自变量的取值范围
8.【答案】5750
【知识点】一次函数的实际应用
9.【答案】-4≤k<1且k≠0
【知识点】一次函数与不等式(组)的综合应用;两一次函数图象相交或平行问题
10.【答案】①②③
【知识点】一次函数与一元一次方程的综合应用;一次函数与不等式(组)的综合应用
11.【答案】解:设y与x的函数关系式为,
∵当时,,
∴,
∴,
∴y与x的函数关系式为,
∴当时,.
【知识点】正比例函数的图象和性质
12.【答案】(1)解:a=900÷45=20,
即a的值是20
(2)1100;50
(3)解:周老师从学校到家用的总的时间为:50+1100÷110=50+10=60(分钟),
周老师从学校到家的平均速度是2000÷60= (米/分钟),
即周老师从学校到家的平均速度是 米/分钟.
【知识点】一次函数的实际应用;通过函数图象获取信息并解决问题
13.【答案】解:设 ( 是常数且 ),
把 , 代入,得 ,解得 ,
所以 ,所以 关于 的函数表达式为
【知识点】待定系数法求一次函数解析式;正比例函数的定义
14.【答案】解:(1)由题意: ,
解得:,
所以E(1,2);
(2)作B关于x轴的对称点B1,连接B1E交x轴于F,
∵y=x+1中,B(0,1)
∴B1(﹣1,0),
设yBE=kx+b(k≠0),
可得:,
∴,
∴y=3x﹣1,
当y=0时,x=,
∴OF=;
(3)当P在直线AE下方时:=+==6,
yP=﹣2,
所以P1(3,﹣2),
当P在直线AE上方时:
=-=|yp-2|,
yP=6,
所以P2(﹣1,6)
【知识点】两一次函数图象相交或平行问题
15.【答案】(1)解: 米/分.
甲离小区路程: 米.
(2)解: 米,
设 ,
代入 , ,
得: ,
解得: ,
.
(3)解:乙步行的速度为: 80-5=75(米/分) ,
乙到达学校用的时间为: (分)
当x=24时,
故s与x的函数图象过(24,80)
当x=25时,甲乙均到达学校,故s=0
故s与x的函数图象过(25,0)
当20≤x≤25时s关于x的函数的大致图象如图所示:
【知识点】待定系数法求一次函数解析式;通过函数图象获取信息并解决问题
16.【答案】(1)解:由y1=﹣ x+1,
可知当y=0时,x=2,
∴点A的坐标是(2,0),
∴AO=2,
∵y1=﹣ x+1与直线y2=﹣ x交于点B,
∴B点的坐标是(﹣1,1.5),
∴△AOB的面积= ×2×1.5=1.5
(2)解:由(1)可知交点B的坐标是(﹣1,1.5),
由函数图象可知y1>y2时x>﹣1
【知识点】一次函数与不等式(组)的综合应用
17.【答案】(1)解:由题意得,,
设直线的表达式为.
把,代入表达式,得,解得,
所以直线的表达式为.
(2)解:,,
当时,
,,或.
点的纵坐标为2或,当点的纵坐标为2时,,解得;
当点的纵坐标为时,,解得,
点的坐标为或.
【知识点】点的坐标;待定系数法求一次函数解析式;三角形的面积
18.【答案】(1)3;6
(2)解:当时,即有,
解得:,即,
∵,,,
∴结合图象可得;
(3)解:点P在线段AD上,∠CAP是锐角,若△ACP是直角三角形,则∠APC=90°或∠ACP=90°,
当y1=0时,即有x+2=0,
解得x=-2,
∴点A(-2,0)
设点,且,
∵,,
∴,,,
当时,轴,
∴点C与点P的横坐标相等,即,
∴,
∴点P坐标为;
当时,,
∴,
解得,
∴点P坐标为;
综上所述,所有符合条件的点P坐标为或.
【知识点】一次函数与不等式(组)的综合应用;两一次函数图象相交或平行问题;勾股定理
19.【答案】(1)解: ,
,
,
,
,
,
设直线 的解析式为: ,
代入点 ,得 ,
,
直线 的解析式为: ;
(2)如图1,过 作 轴于 ,
轴,
,
四边形 为矩形,
,
由题可得, ,
,
又 ,
,
在 与 中,
,
,
,
令 ,
则 ,
,
,
,
;
(3)如图2,连接 ,取 中点 ,连接 , ,
则在 中, ,
同理, ,
,
, , , 四点共圆,
, ,
, ,
,
,
,
,
,
,
又 ,
,
在 上取一点 ,使 ,
则 ,
,
,
,
,则 , ,
,
,
,
,
解得, ,
直线 解析式为: ,
,
则直线 解析式为: ,
联立 ,
解得 ,
.
【知识点】待定系数法求一次函数解析式;一次函数-动态几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【浙教版八上同步练习】
第五章一次函数检测题(培优)
一、单选题
1.若方程ax+b=0的解是x=﹣2,则图中一定不是直线y=ax+b的是( )
A. B.
C. D.
2.直线y=kx+b交坐标轴于A(﹣8,0),B(0,13)两点,则不等式kx+b≥0的解集为( )
A.x≥﹣8 B.x≤﹣8 C.x≥13 D.x≤13
3.如图(1),四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图(2)所示,当P运动到BC中点时,△APD的面积为( )
A.4 B.5 C.6 D.7
4.已知直线y=kx+b经过第一、二、四象限,那么直线y=bx+k一定不经过( )
A.第一象限; B.第二象限; C.第三象限; D.第四象限.
5.将 的正方形网格如图所示的放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是 ,正方形 的顶点都在格点上,若直线 与正方形 有公共点,则 的值不可能是( )
A. B.1 C. D.
二、填空题
6.甲、乙、丙三名同学观察完某个一次函数的图象,各叙述如下:
甲:函数的图象经过点,;
乙;随的增大而减小;
丙:函数的图象不经过第三象限.
根据他们的叙述写出满足上述性质的一个函数表达式为 .
7.在函数y=中,自变量x的取值范围是
8.某厂家以A、B两种原料,利用不同的工艺手法生产出了甲、乙两种袋装产品,其中,甲产品每袋含1.5千克A原料、1.5千克B原料;乙产品每袋含2千克A原料、1千克B原料.甲、乙两种产品每袋的成本价分别为袋中两种原料的成本价之和.若甲产品每袋售价72元,则利润率为20%.某节庆日,厂家准备生产若干袋甲产品和乙产品,甲产品和乙产品的数量和不超过100袋,会计在核算成本的时候把A原料和B原料的单价看反了,后面发现如果不看反,那么实际成本比核算时的成本少500元,那么厂家在生产甲乙两种产品时实际成本最多为 元.
9.已知一次函数(为常数,,若当时有,则的取值范围是 .
10.一次函数与交于点A,有下列结论:
①关于x的方程的解为;
②关于x的不等式组的解集为;
③;
④若,则或
其中正确的结论是 .(填写序号)
三、计算题
11.已知y与x成正比例关系,当时,,求:当时y的值.
12.周老师为锻炼身体一直坚持步行上下班.已知学校到周老师家总路程为2000米.一天,周老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.周老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.
(1)求a的值.
(2)b= ;c= .
(3)求周老师从学校到家的平均速度.
四、解答题
13.已知 与 成正比例,且 时, .求 关于 的函数表达式;
14.如图,直线AB:y=x+1与直线CD:y=﹣2x+4交于点E.
(1)求E点坐标;
(2)在x轴上找一点F使得FB+FE最小,求OF的长;
(3)若P为直线CD上一点,当△AEP面积为6时,求P的坐标.
五、作图题
15.甲乙两位老师同住一小区,该小区与学校相距2000米.甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,骑行若干米到达还车点后,立即步行走到学校.已知乙骑车的速度为170米/分,甲步行的速度比乙步行的速度每分钟快5米.设甲步行的时间为 (分),图1中线段 与折线 分别表示甲、乙离小区的路程 (米)与甲步行时间 (分)的函数关系的图象;图2表示甲、乙两人之间的距离 (米)与甲步行时间 (分)的函数关系的图象(不完整),根据图1和图2中所给的信息,解答下列问题:
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求直线 的解析式;
(3)在图2中,画出当 时, 关于 的函数的大致图象.
六、综合题
16.如图,已知直线y1=﹣ x+1与x轴交于点A,与直线y2=﹣ x交于点B.
(1)求△AOB的面积;
(2)求y1>y2时x的取值范围.
17.如图,在平面直角坐标系中,为坐标原点,,为坐标轴上两点,且,连接.
(1)求直线的函数表达式.
(2)直线上是否存在点使得的面积为面积的,若存在,求出点的坐标;若不存在,请说明理由.
18.如图,在平面直角坐标系中,一次函数的图象与x轴,y轴分别交于点A,B,的图象与x轴,y轴分别交于点D,E,且两个函数图象相交于点.
(1)填空: , ;
(2)x满足什么条件时,;
(3)点P在线段AD上,连接CP,若是直角三角形,求点P的坐标.
19.在平面直角坐标系中, 为坐标原点直线 与 轴交于点 ,与 轴交于点 , , 的面积为2.
(1)如图1,求直线 的解析式;
(2)如图2,线段 上有一点 ,直线 为 , 轴,将 绕点 顺时针旋转 ,交 于点 ,求点 的坐标.(用含 的式子表示)
(3)如图3,在(2)的条件下,连接 ,交直线 于点 ,若 ,求点 的坐标.
答案解析部分
1.【答案】B
【知识点】一次函数与一元一次方程的综合应用
2.【答案】A
【知识点】一次函数与不等式(组)的综合应用
3.【答案】B
【知识点】通过函数图象获取信息并解决问题
4.【答案】B
【知识点】两一次函数图象相交或平行问题;一次函数图象与坐标轴交点问题
5.【答案】D
【知识点】一次函数图象、性质与系数的关系
6.【答案】(答案不唯一)
【知识点】列一次函数关系式;一次函数图象、性质与系数的关系
7.【答案】x≥4
【知识点】函数自变量的取值范围
8.【答案】5750
【知识点】一次函数的实际应用
9.【答案】-4≤k<1且k≠0
【知识点】一次函数与不等式(组)的综合应用;两一次函数图象相交或平行问题
10.【答案】①②③
【知识点】一次函数与一元一次方程的综合应用;一次函数与不等式(组)的综合应用
11.【答案】解:设y与x的函数关系式为,
∵当时,,
∴,
∴,
∴y与x的函数关系式为,
∴当时,.
【知识点】正比例函数的图象和性质
12.【答案】(1)解:a=900÷45=20,
即a的值是20
(2)1100;50
(3)解:周老师从学校到家用的总的时间为:50+1100÷110=50+10=60(分钟),
周老师从学校到家的平均速度是2000÷60= (米/分钟),
即周老师从学校到家的平均速度是 米/分钟.
【知识点】一次函数的实际应用;通过函数图象获取信息并解决问题
13.【答案】解:设 ( 是常数且 ),
把 , 代入,得 ,解得 ,
所以 ,所以 关于 的函数表达式为
【知识点】待定系数法求一次函数解析式;正比例函数的定义
14.【答案】解:(1)由题意: ,
解得:,
所以E(1,2);
(2)作B关于x轴的对称点B1,连接B1E交x轴于F,
∵y=x+1中,B(0,1)
∴B1(﹣1,0),
设yBE=kx+b(k≠0),
可得:,
∴,
∴y=3x﹣1,
当y=0时,x=,
∴OF=;
(3)当P在直线AE下方时:=+==6,
yP=﹣2,
所以P1(3,﹣2),
当P在直线AE上方时:
=-=|yp-2|,
yP=6,
所以P2(﹣1,6)
【知识点】两一次函数图象相交或平行问题
15.【答案】(1)解: 米/分.
甲离小区路程: 米.
(2)解: 米,
设 ,
代入 , ,
得: ,
解得: ,
.
(3)解:乙步行的速度为: 80-5=75(米/分) ,
乙到达学校用的时间为: (分)
当x=24时,
故s与x的函数图象过(24,80)
当x=25时,甲乙均到达学校,故s=0
故s与x的函数图象过(25,0)
当20≤x≤25时s关于x的函数的大致图象如图所示:
【知识点】待定系数法求一次函数解析式;通过函数图象获取信息并解决问题
16.【答案】(1)解:由y1=﹣ x+1,
可知当y=0时,x=2,
∴点A的坐标是(2,0),
∴AO=2,
∵y1=﹣ x+1与直线y2=﹣ x交于点B,
∴B点的坐标是(﹣1,1.5),
∴△AOB的面积= ×2×1.5=1.5
(2)解:由(1)可知交点B的坐标是(﹣1,1.5),
由函数图象可知y1>y2时x>﹣1
【知识点】一次函数与不等式(组)的综合应用
17.【答案】(1)解:由题意得,,
设直线的表达式为.
把,代入表达式,得,解得,
所以直线的表达式为.
(2)解:,,
当时,
,,或.
点的纵坐标为2或,当点的纵坐标为2时,,解得;
当点的纵坐标为时,,解得,
点的坐标为或.
【知识点】点的坐标;待定系数法求一次函数解析式;三角形的面积
18.【答案】(1)3;6
(2)解:当时,即有,
解得:,即,
∵,,,
∴结合图象可得;
(3)解:点P在线段AD上,∠CAP是锐角,若△ACP是直角三角形,则∠APC=90°或∠ACP=90°,
当y1=0时,即有x+2=0,
解得x=-2,
∴点A(-2,0)
设点,且,
∵,,
∴,,,
当时,轴,
∴点C与点P的横坐标相等,即,
∴,
∴点P坐标为;
当时,,
∴,
解得,
∴点P坐标为;
综上所述,所有符合条件的点P坐标为或.
【知识点】一次函数与不等式(组)的综合应用;两一次函数图象相交或平行问题;勾股定理
19.【答案】(1)解: ,
,
,
,
,
,
设直线 的解析式为: ,
代入点 ,得 ,
,
直线 的解析式为: ;
(2)如图1,过 作 轴于 ,
轴,
,
四边形 为矩形,
,
由题可得, ,
,
又 ,
,
在 与 中,
,
,
,
令 ,
则 ,
,
,
,
;
(3)如图2,连接 ,取 中点 ,连接 , ,
则在 中, ,
同理, ,
,
, , , 四点共圆,
, ,
, ,
,
,
,
,
,
,
又 ,
,
在 上取一点 ,使 ,
则 ,
,
,
,
,则 , ,
,
,
,
,
解得, ,
直线 解析式为: ,
,
则直线 解析式为: ,
联立 ,
解得 ,
.
【知识点】待定系数法求一次函数解析式;一次函数-动态几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
