【浙教版九上同步练习】 1.4 二次函数的应用(含答案)
文档属性
| 名称 | 【浙教版九上同步练习】 1.4 二次函数的应用(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-30 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
【浙教版九上同步练习】
1.4二次函数的应用
一、单选题
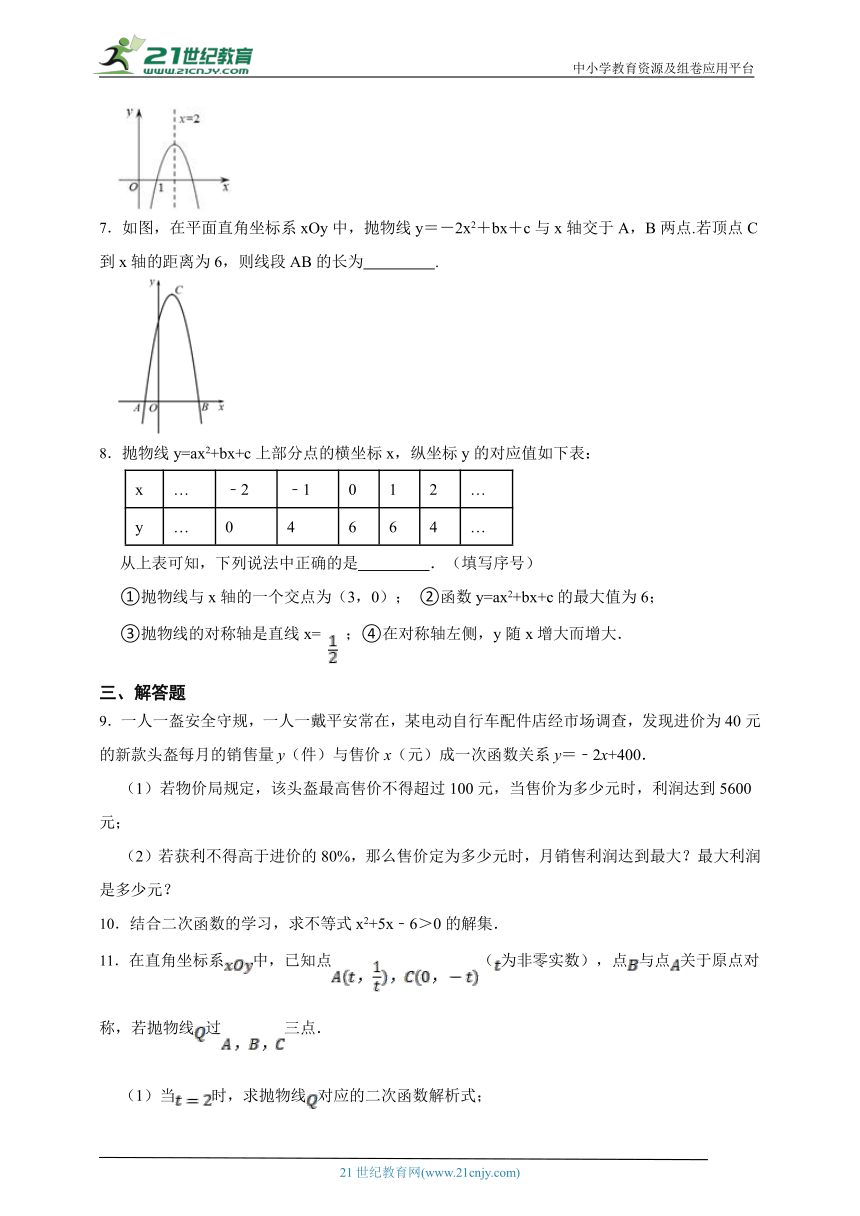
1.已知二次函数的图象(0≤x≤3)如图所示,关于该函数在所给自变量的取值范围内,下列说法正确的是( )
A.有最小值0,有最大值3 B.有最小值-1,有最大值0
C.有最小值-1,有最大值3 D.有最小值-1,无有最大值
2.二次函数y=x2+2x﹣1的最小值是( )
A.﹣1 B.﹣2 C.1 D.2
3.二次函数y=x2﹣2x﹣3图象与y轴的交点坐标是( )
A.(0,1) B.(1,0) C.(-3,0) D.(0,-3)
4.小梦同学观察下表数列的前五个数时,发现an是n的二次函数.设S=,下列说法正确的是( )
n 1 2 3 4 5 … n
数列 -5 -2 0 1 1 … an
A.S有最大值为1 B.当n=10时,S=-14
C.S有最小值为-5 D.当n=15时,S=
二、填空题
5.某种火箭背向上发射时,它的高度h(m)与时间t(s)的关系可以用公式h=﹣5t2+160t+10表示.经过 s,火箭到达它的最高点.
6.如图,在平面直角坐标系 中,抛物线 的对称轴为直线 ,与x轴的一个交点为 ,则关于x的方程 的解为 .
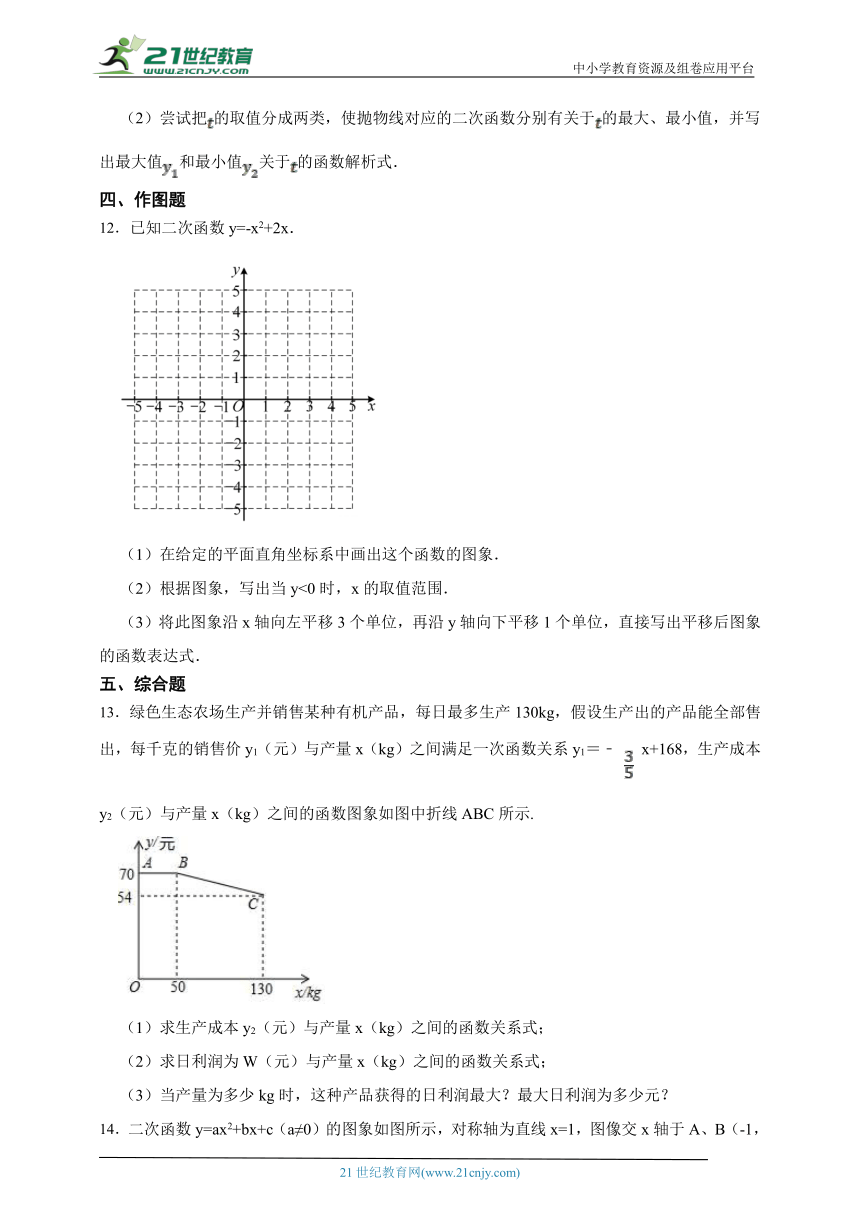
7.如图,在平面直角坐标系xOy中,抛物线y=-2x2+bx+c与x轴交于A,B两点.若顶点C到x轴的距离为6,则线段AB的长为 .
8.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x … ﹣2 ﹣1 0 1 2 …
y … 0 4 6 6 4 …
从上表可知,下列说法中正确的是 .(填写序号)
①抛物线与x轴的一个交点为(3,0); ②函数y=ax2+bx+c的最大值为6;
③抛物线的对称轴是直线x= ;④在对称轴左侧,y随x增大而增大.
三、解答题
9.一人一盔安全守规,一人一戴平安常在,某电动自行车配件店经市场调查,发现进价为40元的新款头盔每月的销售量y(件)与售价x(元)成一次函数关系y=﹣2x+400.
(1)若物价局规定,该头盔最高售价不得超过100元,当售价为多少元时,利润达到5600元;
(2)若获利不得高于进价的80%,那么售价定为多少元时,月销售利润达到最大?最大利润是多少元?
10.结合二次函数的学习,求不等式x2+5x﹣6>0的解集.
11.在直角坐标系中,已知点(为非零实数),点与点关于原点对称,若抛物线过三点.
(1)当时,求抛物线对应的二次函数解析式;
(2)尝试把的取值分成两类,使抛物线对应的二次函数分别有关于的最大、最小值,并写出最大值和最小值关于的函数解析式.
四、作图题
12.已知二次函数y=-x2+2x.
(1)在给定的平面直角坐标系中画出这个函数的图象.
(2)根据图象,写出当y<0时,x的取值范围.
(3)将此图象沿x轴向左平移3个单位,再沿y轴向下平移1个单位,直接写出平移后图象的函数表达式.
五、综合题
13.绿色生态农场生产并销售某种有机产品,每日最多生产130kg,假设生产出的产品能全部售出,每千克的销售价y1(元)与产量x(kg)之间满足一次函数关系y1=﹣ x+168,生产成本y2(元)与产量x(kg)之间的函数图象如图中折线ABC所示.
(1)求生产成本y2(元)与产量x(kg)之间的函数关系式;
(2)求日利润为W(元)与产量x(kg)之间的函数关系式;
(3)当产量为多少kg时,这种产品获得的日利润最大?最大日利润为多少元?
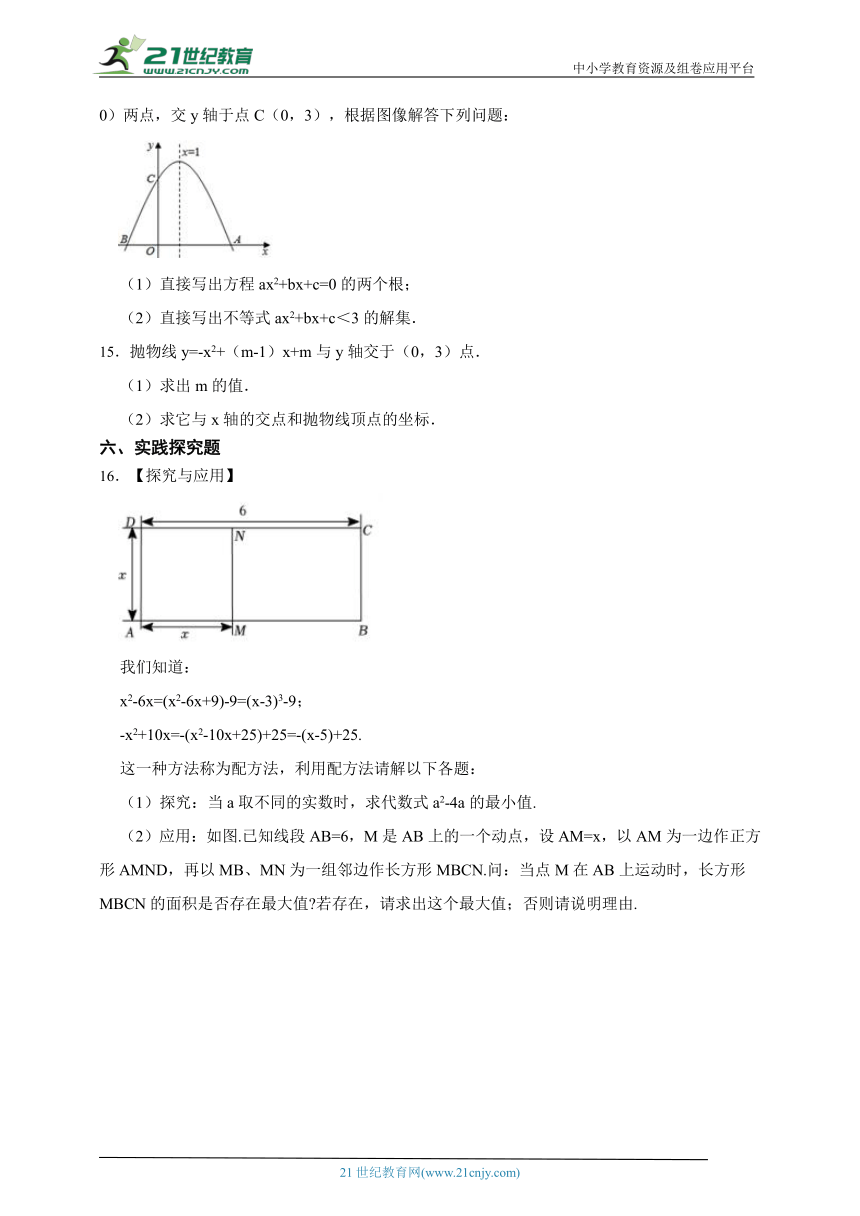
14.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1,图像交x轴于A、B(-1,0)两点,交y轴于点C(0,3),根据图像解答下列问题:
(1)直接写出方程ax2+bx+c=0的两个根;
(2)直接写出不等式ax2+bx+c<3的解集.
15.抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
(1)求出m的值.
(2)求它与x轴的交点和抛物线顶点的坐标.
六、实践探究题
16.【探究与应用】
我们知道:
x2-6x=(x2-6x+9)-9=(x-3)3-9;
-x2+10x=-(x2-10x+25)+25=-(x-5)+25.
这一种方法称为配方法,利用配方法请解以下各题:
(1)探究:当a取不同的实数时,求代数式a2-4a的最小值.
(2)应用:如图.已知线段AB=6,M是AB上的一个动点,设AM=x,以AM为一边作正方形AMND,再以MB、MN为一组邻边作长方形MBCN.问:当点M在AB上运动时,长方形MBCN的面积是否存在最大值 若存在,请求出这个最大值;否则请说明理由.
答案解析部分
1.【答案】C
【知识点】二次函数的最值
2.【答案】B
【知识点】二次函数的最值
3.【答案】D
【知识点】二次函数图象与坐标轴的交点问题
4.【答案】D
【知识点】二次函数的最值;待定系数法求二次函数解析式
5.【答案】16
【知识点】二次函数的最值
6.【答案】 ,
【知识点】二次函数图象与一元二次方程的综合应用
7.【答案】
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=ax^2+bx+c的性质
8.【答案】①③④
【知识点】二次函数的最值;二次函数y=ax^2+bx+c的性质
9.【答案】(1)解:依题意得(x﹣40)(﹣2x+400)=5600,
整理得:x2﹣240x+10800=0,
解得x=60或180,
∵物价局规定,该头盔最高售价不得超过100元,
∴x=180不合题意舍去,
答:当售价为60元时,利润达到5600元.
(2)解:设利润为W元,则W=(x﹣40)(﹣2x+400)=﹣2(x﹣120)2+12800,
∵40×(1+80%)=72,
x≤72,
∵﹣2<0,
∴当x=72时,W最大=8192,
答:售价定为72元时,月销售利润最大为8192元.
【知识点】一元二次方程的实际应用-销售问题;二次函数的实际应用-销售问题
10.【答案】解:设y=x2+5x﹣6,函数图象如图所示:
由函数图象可知不等式x2+5x﹣6>0的解集为x>1或x<﹣6。
【知识点】二次函数与不等式(组)的综合应用
11.【答案】(1)解:设二次函数的关系式为,
∵点和点B关于x轴对称,
∴点B的坐标为.
∵抛物线Q过A,B,C三点,得
解得
∴抛物的关系式为.
当时,抛物线的关系式为;
(2)解:①当时,抛物线开口向上,函数有最小值,
即;
②当时,抛物线开口向下,函数有最大值,
即.
【知识点】二次函数的最值;待定系数法求二次函数解析式;二次函数y=ax^2+bx+c的性质
12.【答案】(1)解 : y=-x2+2x =-x(x-2),
当y=0时,-x(x-2)=0,
解得:x=0或x=2,
∴抛物线与x轴的交点坐标为:(0,0),(2,0),
∴对称轴为x=1,
当x=1时,y=-1+2=1,
∴顶点坐标为:(1,1),
故函数图象如图所示:
(2)解:∵抛物线与x轴的交点坐标为:(0,0),(2,0),抛物线开口向下,
∴当x<0或x>2时,y<0;
∴当y<0时,x的取值范围:x<0或x>2.
(3)y=-(x+2)2.
【知识点】二次函数图象的几何变换;二次函数图象与坐标轴的交点问题;二次函数与不等式(组)的综合应用;二次函数y=ax^2+bx+c的图象
13.【答案】(1)解:由题意,可得当 时, ;
当 时,设 与 之间的函数关系式为 ,
,解得 ,
当 时, .
综上所述,生产成本 (元)与产量 之间的函数关系式为 ;
(2)解: 当 时, ,
当 时,
(3)解: 当 时, ,
当 时,
当 时, 的值最大,最大值为 ;
因此当该产品产量为 时,获得的利润最大,最大值为 元.
【知识点】待定系数法求一次函数解析式;二次函数的最值;二次函数与一次函数的综合应用
14.【答案】(1)解:B(-1,0),对称轴为直线x=1,则点A(3,0),故ax2+bx+c=0的两个根为x1=3、x2=-1
(2)解:点C(0,3),则点C关于对称轴的对称点为:(2,3),则不等式ax2+bx+c<3的解集
为x<0或x>2
【知识点】二次函数与不等式(组)的综合应用;二次函数图象与一元二次方程的综合应用
15.【答案】(1)解:把(0,3)代入y=-x2+(m-1)x+m得,m=3.
∴ y=-x2+2x+3
(2)解:当y=0时,0=-x2+2x+3.解得, ,
∴ 抛物线与x轴的交点是(-1,0)(3,0)
当 时,
∴ 抛物线的顶点是(1,4)
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=ax^2+bx+c与二次函数y=a(x-h)^2+k的转化
16.【答案】(1)解:∵4a
=4a+44
=4
答:当时,代数式存在最小值为-4;
(2)设长方形的面积为,
根据题意得:
(x-3)2+99,
则时,存在最大值,最大值为9.
答:长方形的面积存在最大值,最大值为9.
【知识点】二次函数的最值;配方法的应用;二次函数的实际应用-几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【浙教版九上同步练习】
1.4二次函数的应用
一、单选题
1.已知二次函数的图象(0≤x≤3)如图所示,关于该函数在所给自变量的取值范围内,下列说法正确的是( )
A.有最小值0,有最大值3 B.有最小值-1,有最大值0
C.有最小值-1,有最大值3 D.有最小值-1,无有最大值
2.二次函数y=x2+2x﹣1的最小值是( )
A.﹣1 B.﹣2 C.1 D.2
3.二次函数y=x2﹣2x﹣3图象与y轴的交点坐标是( )
A.(0,1) B.(1,0) C.(-3,0) D.(0,-3)
4.小梦同学观察下表数列的前五个数时,发现an是n的二次函数.设S=,下列说法正确的是( )
n 1 2 3 4 5 … n
数列 -5 -2 0 1 1 … an
A.S有最大值为1 B.当n=10时,S=-14
C.S有最小值为-5 D.当n=15时,S=
二、填空题
5.某种火箭背向上发射时,它的高度h(m)与时间t(s)的关系可以用公式h=﹣5t2+160t+10表示.经过 s,火箭到达它的最高点.
6.如图,在平面直角坐标系 中,抛物线 的对称轴为直线 ,与x轴的一个交点为 ,则关于x的方程 的解为 .
7.如图,在平面直角坐标系xOy中,抛物线y=-2x2+bx+c与x轴交于A,B两点.若顶点C到x轴的距离为6,则线段AB的长为 .
8.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x … ﹣2 ﹣1 0 1 2 …
y … 0 4 6 6 4 …
从上表可知,下列说法中正确的是 .(填写序号)
①抛物线与x轴的一个交点为(3,0); ②函数y=ax2+bx+c的最大值为6;
③抛物线的对称轴是直线x= ;④在对称轴左侧,y随x增大而增大.
三、解答题
9.一人一盔安全守规,一人一戴平安常在,某电动自行车配件店经市场调查,发现进价为40元的新款头盔每月的销售量y(件)与售价x(元)成一次函数关系y=﹣2x+400.
(1)若物价局规定,该头盔最高售价不得超过100元,当售价为多少元时,利润达到5600元;
(2)若获利不得高于进价的80%,那么售价定为多少元时,月销售利润达到最大?最大利润是多少元?
10.结合二次函数的学习,求不等式x2+5x﹣6>0的解集.
11.在直角坐标系中,已知点(为非零实数),点与点关于原点对称,若抛物线过三点.
(1)当时,求抛物线对应的二次函数解析式;
(2)尝试把的取值分成两类,使抛物线对应的二次函数分别有关于的最大、最小值,并写出最大值和最小值关于的函数解析式.
四、作图题
12.已知二次函数y=-x2+2x.
(1)在给定的平面直角坐标系中画出这个函数的图象.
(2)根据图象,写出当y<0时,x的取值范围.
(3)将此图象沿x轴向左平移3个单位,再沿y轴向下平移1个单位,直接写出平移后图象的函数表达式.
五、综合题
13.绿色生态农场生产并销售某种有机产品,每日最多生产130kg,假设生产出的产品能全部售出,每千克的销售价y1(元)与产量x(kg)之间满足一次函数关系y1=﹣ x+168,生产成本y2(元)与产量x(kg)之间的函数图象如图中折线ABC所示.
(1)求生产成本y2(元)与产量x(kg)之间的函数关系式;
(2)求日利润为W(元)与产量x(kg)之间的函数关系式;
(3)当产量为多少kg时,这种产品获得的日利润最大?最大日利润为多少元?
14.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1,图像交x轴于A、B(-1,0)两点,交y轴于点C(0,3),根据图像解答下列问题:
(1)直接写出方程ax2+bx+c=0的两个根;
(2)直接写出不等式ax2+bx+c<3的解集.
15.抛物线y=-x2+(m-1)x+m与y轴交于(0,3)点.
(1)求出m的值.
(2)求它与x轴的交点和抛物线顶点的坐标.
六、实践探究题
16.【探究与应用】
我们知道:
x2-6x=(x2-6x+9)-9=(x-3)3-9;
-x2+10x=-(x2-10x+25)+25=-(x-5)+25.
这一种方法称为配方法,利用配方法请解以下各题:
(1)探究:当a取不同的实数时,求代数式a2-4a的最小值.
(2)应用:如图.已知线段AB=6,M是AB上的一个动点,设AM=x,以AM为一边作正方形AMND,再以MB、MN为一组邻边作长方形MBCN.问:当点M在AB上运动时,长方形MBCN的面积是否存在最大值 若存在,请求出这个最大值;否则请说明理由.
答案解析部分
1.【答案】C
【知识点】二次函数的最值
2.【答案】B
【知识点】二次函数的最值
3.【答案】D
【知识点】二次函数图象与坐标轴的交点问题
4.【答案】D
【知识点】二次函数的最值;待定系数法求二次函数解析式
5.【答案】16
【知识点】二次函数的最值
6.【答案】 ,
【知识点】二次函数图象与一元二次方程的综合应用
7.【答案】
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=ax^2+bx+c的性质
8.【答案】①③④
【知识点】二次函数的最值;二次函数y=ax^2+bx+c的性质
9.【答案】(1)解:依题意得(x﹣40)(﹣2x+400)=5600,
整理得:x2﹣240x+10800=0,
解得x=60或180,
∵物价局规定,该头盔最高售价不得超过100元,
∴x=180不合题意舍去,
答:当售价为60元时,利润达到5600元.
(2)解:设利润为W元,则W=(x﹣40)(﹣2x+400)=﹣2(x﹣120)2+12800,
∵40×(1+80%)=72,
x≤72,
∵﹣2<0,
∴当x=72时,W最大=8192,
答:售价定为72元时,月销售利润最大为8192元.
【知识点】一元二次方程的实际应用-销售问题;二次函数的实际应用-销售问题
10.【答案】解:设y=x2+5x﹣6,函数图象如图所示:
由函数图象可知不等式x2+5x﹣6>0的解集为x>1或x<﹣6。
【知识点】二次函数与不等式(组)的综合应用
11.【答案】(1)解:设二次函数的关系式为,
∵点和点B关于x轴对称,
∴点B的坐标为.
∵抛物线Q过A,B,C三点,得
解得
∴抛物的关系式为.
当时,抛物线的关系式为;
(2)解:①当时,抛物线开口向上,函数有最小值,
即;
②当时,抛物线开口向下,函数有最大值,
即.
【知识点】二次函数的最值;待定系数法求二次函数解析式;二次函数y=ax^2+bx+c的性质
12.【答案】(1)解 : y=-x2+2x =-x(x-2),
当y=0时,-x(x-2)=0,
解得:x=0或x=2,
∴抛物线与x轴的交点坐标为:(0,0),(2,0),
∴对称轴为x=1,
当x=1时,y=-1+2=1,
∴顶点坐标为:(1,1),
故函数图象如图所示:
(2)解:∵抛物线与x轴的交点坐标为:(0,0),(2,0),抛物线开口向下,
∴当x<0或x>2时,y<0;
∴当y<0时,x的取值范围:x<0或x>2.
(3)y=-(x+2)2.
【知识点】二次函数图象的几何变换;二次函数图象与坐标轴的交点问题;二次函数与不等式(组)的综合应用;二次函数y=ax^2+bx+c的图象
13.【答案】(1)解:由题意,可得当 时, ;
当 时,设 与 之间的函数关系式为 ,
,解得 ,
当 时, .
综上所述,生产成本 (元)与产量 之间的函数关系式为 ;
(2)解: 当 时, ,
当 时,
(3)解: 当 时, ,
当 时,
当 时, 的值最大,最大值为 ;
因此当该产品产量为 时,获得的利润最大,最大值为 元.
【知识点】待定系数法求一次函数解析式;二次函数的最值;二次函数与一次函数的综合应用
14.【答案】(1)解:B(-1,0),对称轴为直线x=1,则点A(3,0),故ax2+bx+c=0的两个根为x1=3、x2=-1
(2)解:点C(0,3),则点C关于对称轴的对称点为:(2,3),则不等式ax2+bx+c<3的解集
为x<0或x>2
【知识点】二次函数与不等式(组)的综合应用;二次函数图象与一元二次方程的综合应用
15.【答案】(1)解:把(0,3)代入y=-x2+(m-1)x+m得,m=3.
∴ y=-x2+2x+3
(2)解:当y=0时,0=-x2+2x+3.解得, ,
∴ 抛物线与x轴的交点是(-1,0)(3,0)
当 时,
∴ 抛物线的顶点是(1,4)
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=ax^2+bx+c与二次函数y=a(x-h)^2+k的转化
16.【答案】(1)解:∵4a
=4a+44
=4
答:当时,代数式存在最小值为-4;
(2)设长方形的面积为,
根据题意得:
(x-3)2+99,
则时,存在最大值,最大值为9.
答:长方形的面积存在最大值,最大值为9.
【知识点】二次函数的最值;配方法的应用;二次函数的实际应用-几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
