【浙教版九上同步练习】 2.4 概率的简单应用(含答案)
文档属性
| 名称 | 【浙教版九上同步练习】 2.4 概率的简单应用(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-30 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【浙教版九上同步练习】
2.4概率的简单应用
一、单选题
1.在一个不透明的盒子里有3个红球和若干个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个,摸到红球的概率是 ,则白球的个数是( )
A.3 B.4 C.6 D.9
2.在一个不透明的布袋中,共有30个小球,除颜色外其他完全相同 若每次将球搅匀后摸一个球记下颜色再放回布袋 通过大量重复摸球试验后发现,摸到红色球的频率稳定在 左右,则口袋中红色球的个数应该是
A.6个 B.15个 C.24个 D.12个
3.据有关部门门]统计,某地61岁老人的死亡概率约为,若10000个61岁老人参加寿险投保,当年死亡的人均赔偿金为a元,则估计保险公司需支付当年死亡的人的赔偿金为( ).
A.80a元 B.100a元 C.125a元 D.250a 元
4.甲、乙两所医院分别有一男一女共 名医护人员支援湖北武汉抗击疫情,若从甲、乙两医院支援的医护人员中分别随机选 名,则所选的 名医护人员性别相同的概率是( )
A. B. C. D.
二、填空题
5.一枚质地均匀的骰子的6个面上分别刻有1 6的点数,抛掷这枚骰子1次,向上一面的点数大于2且小于5的概率是 .
6.一个口袋中有红球、白球共20个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有70次摸到红球.请你估计这个口袋中有 个白球.
7.在不透明的袋子里装有颜色不同的16个红球和若干个白球,每次从袋子里摸出1个球,记录下颜色后再放回,经过100次试验,发现摸到白球的次数为60次,估计袋中白球有 个。
8.“石头、剪刀、布”是民间广为流传的一种游戏,游戏时甲乙双方每次做“石头”“剪刀”“布”三种手势中的一种,并约定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛.假定甲、乙两人每次都是等可能地做这三种手势,那么一次游戏中乙获胜的概率是 .
三、解答题
9.《孟子·梁惠王上》中有言“老吾老,以及人之老”,“敬老爱老”是中华民族优良的传统美德,我们要弘扬这优良的传统,为新中国的精神文明建设贡献自己的一份力量.小颖计划利用周末从三个养老中心中,选择一个参加志愿服务活动,但一时间不知道该选择哪个养老中心,于是决定通过转转盘的方法决定.如图,有两个质地均匀的转盘,图①中的转盘被平均分成4份,分别标上数字、、3、4,图②中的转盘被平均分成3份,分别标上数字,小颖分别将两个转盘各转一次,记录下转盘停止转动后指针指向的数字(指针指向两个扇形的交线时视为无效,需重新转动转盘),若两个转盘都停止转动后指针指向的两个数字之积为正数,则去养老中心;若两个转盘都停止转动后指针指向的两个数字之积为负数,则去养老中心;若两个转盘都停止转动后指针指向的两个数字之积为零,则去养老中心.
(1)图①中转盘停止转动后,指针指向的数字大于2的概率为
(2)请用列表法或画树状图的方法求小颖最终去养老中心的概率.
10.已知在直角坐标系中一点 P(a,b),其中a,b可以取-2,-1.1,2中任意一个值(a≠b).求点P(a,b)恰好落在反比例函数y= 的图象上的概率.
11.甲、乙两位同学相约打乒乓球.
(1)有款式完全相同的4个乒乓球拍分别记为,,,,若甲先从中随机选取1个,乙再从余下的球拍中随机选取1个,求乙选中球拍C的概率;
(2)双方约定:两人各投掷一枚质地均匀的硬币,如果两枚硬币全部正面向上或全部反面向上,那么甲先发球,否则乙先发球这个约定是否公平?为什么?
四、作图题
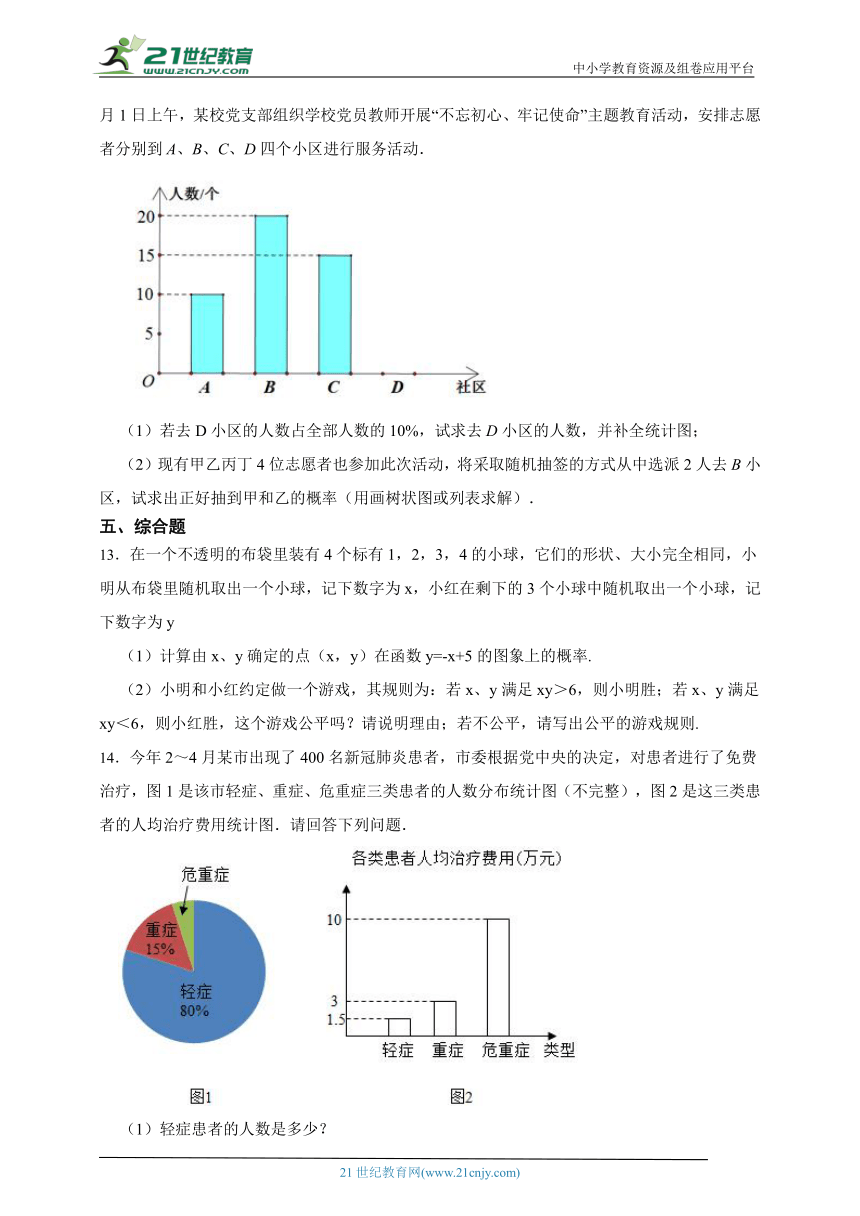
12.为深入学习贯彻习近平新时代中国特色社会主义思想,调动党员教师为民服务的积极性,12月1日上午,某校党支部组织学校党员教师开展“不忘初心、牢记使命”主题教育活动,安排志愿者分别到A、B、C、D四个小区进行服务活动.
(1)若去D小区的人数占全部人数的10%,试求去D小区的人数,并补全统计图;
(2)现有甲乙丙丁4位志愿者也参加此次活动,将采取随机抽签的方式从中选派2人去B小区,试求出正好抽到甲和乙的概率(用画树状图或列表求解).
五、综合题
13.在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同,小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y
(1)计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率.
(2)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜,这个游戏公平吗?请说明理由;若不公平,请写出公平的游戏规则.
14.今年2~4月某市出现了400名新冠肺炎患者,市委根据党中央的决定,对患者进行了免费治疗,图1是该市轻症、重症、危重症三类患者的人数分布统计图(不完整),图2是这三类患者的人均治疗费用统计图.请回答下列问题.
(1)轻症患者的人数是多少?
(2)所有患者的平均治疗费用是多少万元?
(3)由于部分轻症患者康复出院,为减少病房拥挤,拟对某病房中的 、 、 、 、 五位患者任选两位转入另一病房,请用树状图法或列表法求出恰好选中 、 两位患者的概率.
15.小红的爸爸积极参加社区抗疫志愿服务工作.根据社区的安排志愿者被随机分到 组(体温检测)、 组(便民代购)、 组(环境消杀).
(1)小红的爸爸被分到 组的概率是 ;
(2)某中学王老师也参加了该社区的志愿者队伍,他和小红爸爸被分到同一组的概率是多少?(请用画树状图或列表的方法写出分析过程)
六、实践探究题
16.某商场进行“6·18”促销活动,设计了如下两种摇奖方式:
方式一:如图1,有一枚均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这个骰子掷出后,“6”朝上则获奖;
方式二:如图2,一个均匀的转盘被等分成12份,分别标有1,2,3,4,5,6,7,8,9,10,11,12这12个数字.转动转盘,当转盘停止后,指针指向的数字为3的倍数则获奖.
(1)若采用方式一,骰子掷出后,“5”朝上的概率为 ;
(2)若采用方式二,当转盘停止后,指针指向的数字为“5”的概率为 ;
(3)小明想增加获奖机会,应选择哪种摇奖方式?请通过相关计算,应用概率相关知识说明理由.
答案解析部分
1.【答案】C
【知识点】概率的简单应用
2.【答案】A
【知识点】利用频率估计概率;概率的简单应用
3.【答案】C
【知识点】概率的简单应用
4.【答案】A
【知识点】概率的简单应用
5.【答案】
【知识点】概率公式;概率的简单应用
6.【答案】14
【知识点】概率的简单应用
7.【答案】24
【知识点】概率的简单应用
8.【答案】
【知识点】概率的简单应用
9.【答案】(1)
(2)根据题意,画树状图如下:
由树状图可知,共有12种等可能的结果,其中两个转盘都停止转动后指针指向的数字之积为正数的有4种情况,
∴(小颖最终去养老中心).
【知识点】列表法与树状图法;概率的简单应用
10.【答案】解:将点P(a,b)代入反比例函数y= 中得,
b = ,
整理得:ab=2,
点P坐标乘积为2的情况如下表:
-2 -1 1 2
-2 2 -2 -4
-1 2 -1 -2
1 -2 -1 2
2 -4 -2 2
点P(a,b)恰好落在反比例函数y= 的图象上的概率为:.
【知识点】反比例函数的图象;列表法与树状图法;概率的简单应用
11.【答案】(1)解:画树状图如下:
一共有种等可能的结果,其中乙选中球拍有种可能的结果,
∴P(乙选中球拍);
(2)解:公平.理由如下:
画树状图如下:
一共有种等可能的结果,其中两枚硬币全部正面向上或全部反面向上有种可能的结果,
∴P(甲先发球),
∴P(乙先发球),
∵ P(甲先发球)=P(乙先发球),
这个约定公平.
【知识点】列表法与树状图法;游戏公平性;概率的简单应用
12.【答案】(1)解:(10+20+15)÷(1-10%)=50人
50×10%=5人
补全统计图如图所示
(2)解:树状图如图所示
【知识点】频数与频率;条形统计图;概率的简单应用
13.【答案】(1)解:画树形图:
所以共有12个点:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),
其中满足y=-x+6的点有(2,4),(4,2),
所以点(x,y)在函数y=-x+6图象上的概率= =
(2)解:满足xy>6的点有(2,4),(4,2),(4,3),(3,4),共4个;
满足xy<6的点有(1,2),(1,3),(1,4),(2,1),(3,1),(4,1),共6个,
所以P(小明胜)= = ;P(小红胜)= = ;
∵ ≠ ,
∴游戏规则不公平.
游戏规则可改为:若x、y满足xy≥6,则小明胜;若x、y满足xy<6,则小红胜
【知识点】列表法与树状图法;游戏公平性;概率的简单应用
14.【答案】(1)400×80%=320(人),
答:轻症患者的人数为320人.
(2)重症患者为400×15%=60(人),
危重症患者为400-320-60=20(人),
∵三类患者的人均治疗费用分别为1.5万元、3万元、10万元,
∴所有患者的平均治疗费用为 =2.15(万元),
答:所有患者的平均治疗费用为2.15万元.
(3)画树状图如下:
由树状图可知:共有20种等可能的结果,恰好选中B、D两位同学的有2种情况,
∴恰好选中 、 两位患者的概率= .
【知识点】利用统计图表分析实际问题;概率的简单应用
15.【答案】(1)
(2)解:用列表法表示所有可能出现的结果如下:
小红爸爸王老师 A B C
A AA AB AC
B BA BB BC
C CA CB CC
共有9种可能出现的结果,其中“他与小红的爸爸”在同一组的有3种,
∴P(他与小红爸爸在同一组)=
【知识点】列表法与树状图法;概率的简单应用
16.【答案】(1)
(2)
(3)解:应选择方式二,理由如下:
采用方式一,(“6”朝上),
采用方式二,指针指向的数字为3的倍数有3,6,9,12,共4个,
∴(指针指向的数字为3的倍数),
∵,
∴方式二获奖机会大,
∴选方式二.
【知识点】概率的简单应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【浙教版九上同步练习】
2.4概率的简单应用
一、单选题
1.在一个不透明的盒子里有3个红球和若干个白球,这些球除颜色外其余完全相同,摇匀后随机摸出一个,摸到红球的概率是 ,则白球的个数是( )
A.3 B.4 C.6 D.9
2.在一个不透明的布袋中,共有30个小球,除颜色外其他完全相同 若每次将球搅匀后摸一个球记下颜色再放回布袋 通过大量重复摸球试验后发现,摸到红色球的频率稳定在 左右,则口袋中红色球的个数应该是
A.6个 B.15个 C.24个 D.12个
3.据有关部门门]统计,某地61岁老人的死亡概率约为,若10000个61岁老人参加寿险投保,当年死亡的人均赔偿金为a元,则估计保险公司需支付当年死亡的人的赔偿金为( ).
A.80a元 B.100a元 C.125a元 D.250a 元
4.甲、乙两所医院分别有一男一女共 名医护人员支援湖北武汉抗击疫情,若从甲、乙两医院支援的医护人员中分别随机选 名,则所选的 名医护人员性别相同的概率是( )
A. B. C. D.
二、填空题
5.一枚质地均匀的骰子的6个面上分别刻有1 6的点数,抛掷这枚骰子1次,向上一面的点数大于2且小于5的概率是 .
6.一个口袋中有红球、白球共20个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有70次摸到红球.请你估计这个口袋中有 个白球.
7.在不透明的袋子里装有颜色不同的16个红球和若干个白球,每次从袋子里摸出1个球,记录下颜色后再放回,经过100次试验,发现摸到白球的次数为60次,估计袋中白球有 个。
8.“石头、剪刀、布”是民间广为流传的一种游戏,游戏时甲乙双方每次做“石头”“剪刀”“布”三种手势中的一种,并约定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛.假定甲、乙两人每次都是等可能地做这三种手势,那么一次游戏中乙获胜的概率是 .
三、解答题
9.《孟子·梁惠王上》中有言“老吾老,以及人之老”,“敬老爱老”是中华民族优良的传统美德,我们要弘扬这优良的传统,为新中国的精神文明建设贡献自己的一份力量.小颖计划利用周末从三个养老中心中,选择一个参加志愿服务活动,但一时间不知道该选择哪个养老中心,于是决定通过转转盘的方法决定.如图,有两个质地均匀的转盘,图①中的转盘被平均分成4份,分别标上数字、、3、4,图②中的转盘被平均分成3份,分别标上数字,小颖分别将两个转盘各转一次,记录下转盘停止转动后指针指向的数字(指针指向两个扇形的交线时视为无效,需重新转动转盘),若两个转盘都停止转动后指针指向的两个数字之积为正数,则去养老中心;若两个转盘都停止转动后指针指向的两个数字之积为负数,则去养老中心;若两个转盘都停止转动后指针指向的两个数字之积为零,则去养老中心.
(1)图①中转盘停止转动后,指针指向的数字大于2的概率为
(2)请用列表法或画树状图的方法求小颖最终去养老中心的概率.
10.已知在直角坐标系中一点 P(a,b),其中a,b可以取-2,-1.1,2中任意一个值(a≠b).求点P(a,b)恰好落在反比例函数y= 的图象上的概率.
11.甲、乙两位同学相约打乒乓球.
(1)有款式完全相同的4个乒乓球拍分别记为,,,,若甲先从中随机选取1个,乙再从余下的球拍中随机选取1个,求乙选中球拍C的概率;
(2)双方约定:两人各投掷一枚质地均匀的硬币,如果两枚硬币全部正面向上或全部反面向上,那么甲先发球,否则乙先发球这个约定是否公平?为什么?
四、作图题
12.为深入学习贯彻习近平新时代中国特色社会主义思想,调动党员教师为民服务的积极性,12月1日上午,某校党支部组织学校党员教师开展“不忘初心、牢记使命”主题教育活动,安排志愿者分别到A、B、C、D四个小区进行服务活动.
(1)若去D小区的人数占全部人数的10%,试求去D小区的人数,并补全统计图;
(2)现有甲乙丙丁4位志愿者也参加此次活动,将采取随机抽签的方式从中选派2人去B小区,试求出正好抽到甲和乙的概率(用画树状图或列表求解).
五、综合题
13.在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同,小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y
(1)计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率.
(2)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜,这个游戏公平吗?请说明理由;若不公平,请写出公平的游戏规则.
14.今年2~4月某市出现了400名新冠肺炎患者,市委根据党中央的决定,对患者进行了免费治疗,图1是该市轻症、重症、危重症三类患者的人数分布统计图(不完整),图2是这三类患者的人均治疗费用统计图.请回答下列问题.
(1)轻症患者的人数是多少?
(2)所有患者的平均治疗费用是多少万元?
(3)由于部分轻症患者康复出院,为减少病房拥挤,拟对某病房中的 、 、 、 、 五位患者任选两位转入另一病房,请用树状图法或列表法求出恰好选中 、 两位患者的概率.
15.小红的爸爸积极参加社区抗疫志愿服务工作.根据社区的安排志愿者被随机分到 组(体温检测)、 组(便民代购)、 组(环境消杀).
(1)小红的爸爸被分到 组的概率是 ;
(2)某中学王老师也参加了该社区的志愿者队伍,他和小红爸爸被分到同一组的概率是多少?(请用画树状图或列表的方法写出分析过程)
六、实践探究题
16.某商场进行“6·18”促销活动,设计了如下两种摇奖方式:
方式一:如图1,有一枚均匀的正二十面体形状的骰子,其中的1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,5个面标有“5”,其余的面标有“6”.将这个骰子掷出后,“6”朝上则获奖;
方式二:如图2,一个均匀的转盘被等分成12份,分别标有1,2,3,4,5,6,7,8,9,10,11,12这12个数字.转动转盘,当转盘停止后,指针指向的数字为3的倍数则获奖.
(1)若采用方式一,骰子掷出后,“5”朝上的概率为 ;
(2)若采用方式二,当转盘停止后,指针指向的数字为“5”的概率为 ;
(3)小明想增加获奖机会,应选择哪种摇奖方式?请通过相关计算,应用概率相关知识说明理由.
答案解析部分
1.【答案】C
【知识点】概率的简单应用
2.【答案】A
【知识点】利用频率估计概率;概率的简单应用
3.【答案】C
【知识点】概率的简单应用
4.【答案】A
【知识点】概率的简单应用
5.【答案】
【知识点】概率公式;概率的简单应用
6.【答案】14
【知识点】概率的简单应用
7.【答案】24
【知识点】概率的简单应用
8.【答案】
【知识点】概率的简单应用
9.【答案】(1)
(2)根据题意,画树状图如下:
由树状图可知,共有12种等可能的结果,其中两个转盘都停止转动后指针指向的数字之积为正数的有4种情况,
∴(小颖最终去养老中心).
【知识点】列表法与树状图法;概率的简单应用
10.【答案】解:将点P(a,b)代入反比例函数y= 中得,
b = ,
整理得:ab=2,
点P坐标乘积为2的情况如下表:
-2 -1 1 2
-2 2 -2 -4
-1 2 -1 -2
1 -2 -1 2
2 -4 -2 2
点P(a,b)恰好落在反比例函数y= 的图象上的概率为:.
【知识点】反比例函数的图象;列表法与树状图法;概率的简单应用
11.【答案】(1)解:画树状图如下:
一共有种等可能的结果,其中乙选中球拍有种可能的结果,
∴P(乙选中球拍);
(2)解:公平.理由如下:
画树状图如下:
一共有种等可能的结果,其中两枚硬币全部正面向上或全部反面向上有种可能的结果,
∴P(甲先发球),
∴P(乙先发球),
∵ P(甲先发球)=P(乙先发球),
这个约定公平.
【知识点】列表法与树状图法;游戏公平性;概率的简单应用
12.【答案】(1)解:(10+20+15)÷(1-10%)=50人
50×10%=5人
补全统计图如图所示
(2)解:树状图如图所示
【知识点】频数与频率;条形统计图;概率的简单应用
13.【答案】(1)解:画树形图:
所以共有12个点:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),
其中满足y=-x+6的点有(2,4),(4,2),
所以点(x,y)在函数y=-x+6图象上的概率= =
(2)解:满足xy>6的点有(2,4),(4,2),(4,3),(3,4),共4个;
满足xy<6的点有(1,2),(1,3),(1,4),(2,1),(3,1),(4,1),共6个,
所以P(小明胜)= = ;P(小红胜)= = ;
∵ ≠ ,
∴游戏规则不公平.
游戏规则可改为:若x、y满足xy≥6,则小明胜;若x、y满足xy<6,则小红胜
【知识点】列表法与树状图法;游戏公平性;概率的简单应用
14.【答案】(1)400×80%=320(人),
答:轻症患者的人数为320人.
(2)重症患者为400×15%=60(人),
危重症患者为400-320-60=20(人),
∵三类患者的人均治疗费用分别为1.5万元、3万元、10万元,
∴所有患者的平均治疗费用为 =2.15(万元),
答:所有患者的平均治疗费用为2.15万元.
(3)画树状图如下:
由树状图可知:共有20种等可能的结果,恰好选中B、D两位同学的有2种情况,
∴恰好选中 、 两位患者的概率= .
【知识点】利用统计图表分析实际问题;概率的简单应用
15.【答案】(1)
(2)解:用列表法表示所有可能出现的结果如下:
小红爸爸王老师 A B C
A AA AB AC
B BA BB BC
C CA CB CC
共有9种可能出现的结果,其中“他与小红的爸爸”在同一组的有3种,
∴P(他与小红爸爸在同一组)=
【知识点】列表法与树状图法;概率的简单应用
16.【答案】(1)
(2)
(3)解:应选择方式二,理由如下:
采用方式一,(“6”朝上),
采用方式二,指针指向的数字为3的倍数有3,6,9,12,共4个,
∴(指针指向的数字为3的倍数),
∵,
∴方式二获奖机会大,
∴选方式二.
【知识点】概率的简单应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
