{浙教版九上同步练习}3.4 圆心角(含答案)
文档属性
| 名称 | {浙教版九上同步练习}3.4 圆心角(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 15:22:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
{浙教版九上同步练习}
5.4圆心角
一、单选题
1.下列语句中,其中正确的个数是( )
①将多项式a(x﹣y)2﹣b(y﹣x)因式分解,则原式=(x﹣y)(ax﹣ay+b);②将多项式x2+4y2﹣4xy因式分解,则原式=(x﹣2y)2;③90°的圆周角所对的弦是直径;④半圆(或直径)所对的圆周角是直角.
A.1 B.2 C.3 D.4
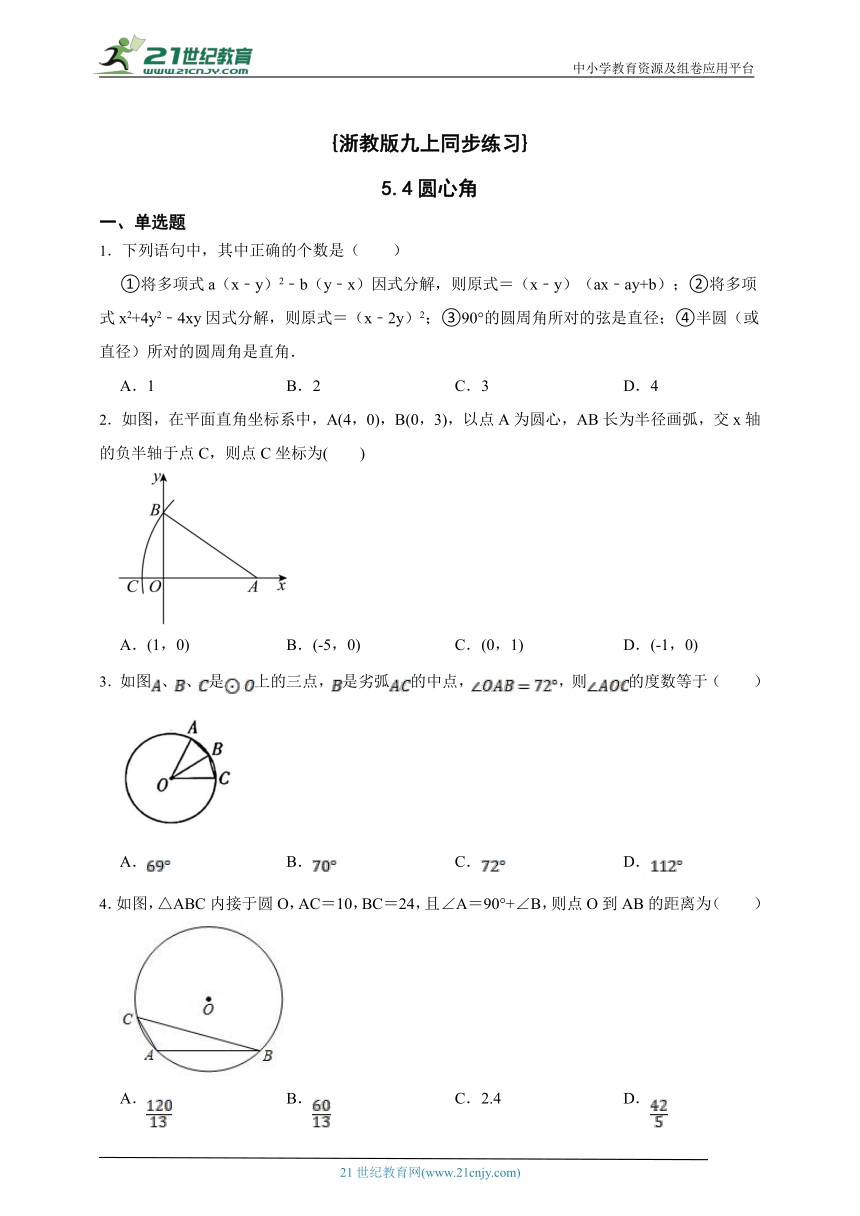
2.如图,在平面直角坐标系中,A(4,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为( )
A.(1,0) B.(-5,0) C.(0,1) D.(-1,0)
3.如图、、是上的三点,是劣弧的中点,,则的度数等于( )
A. B. C. D.
4.如图,△ABC内接于圆O,AC=10,BC=24,且∠A=90°+∠B,则点O到AB的距离为( )
A. B. C.2.4 D.
二、填空题
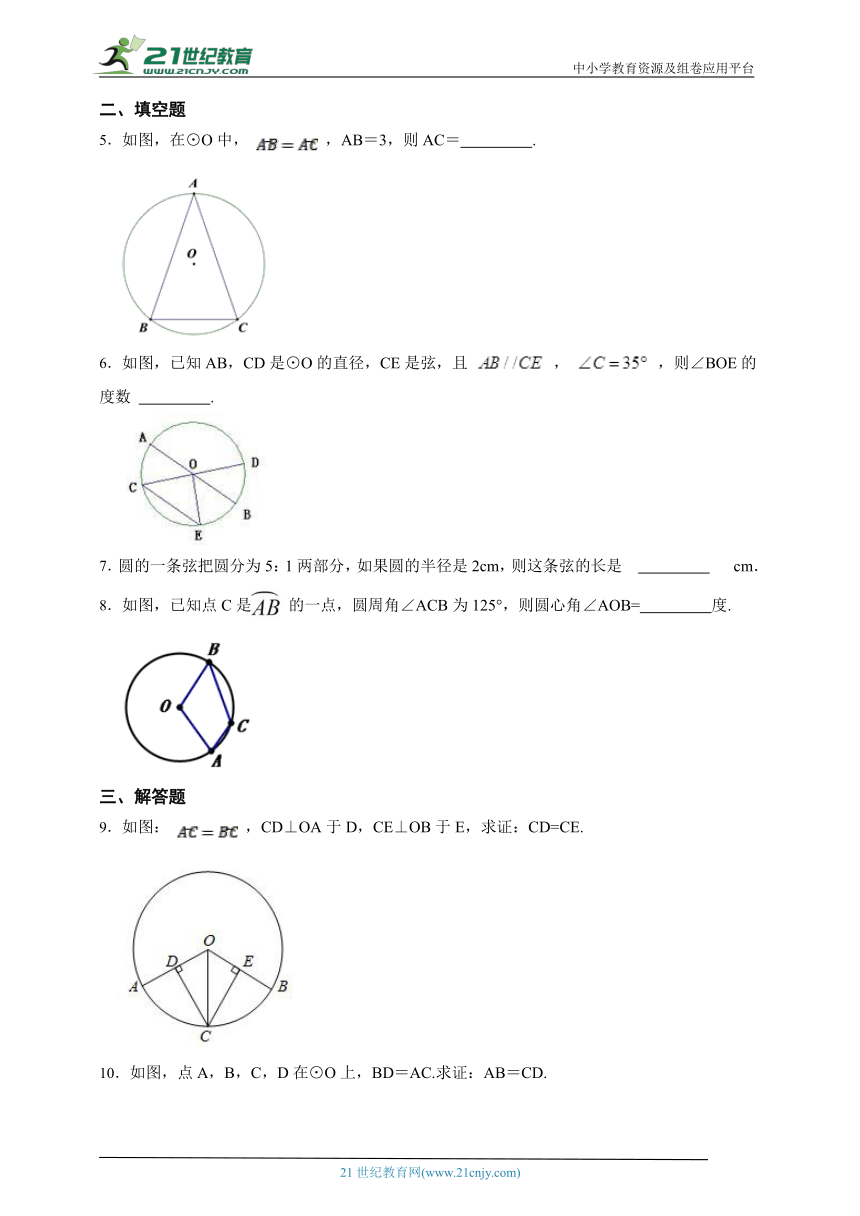
5.如图,在⊙O中, ,AB=3,则AC= .
6.如图,已知AB,CD是⊙O的直径,CE是弦,且 , ,则∠BOE的度数 .
7.圆的一条弦把圆分为5:1两部分,如果圆的半径是2cm,则这条弦的长是 cm.
8.如图,已知点C是 的一点,圆周角∠ACB为125°,则圆心角∠AOB= 度.
三、解答题
9.如图: ,CD⊥OA于D,CE⊥OB于E,求证:CD=CE.
10.如图,点A,B,C,D在⊙O上,BD=AC.求证:AB=CD.
11.如图,⊙O的弦AB、CD的延长线相交于点P,且AB=CD,求证:PB=PD.
四、作图题
12.按要求作图,不要求写作法,但要保留作图痕迹.
(1)如图1,A为圆E上一点,请用直尺(不带刻度)和圆规作出圆内接正方形;
(2)我们知道,三角形具有性质,三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高交于同一点,请运用上述性质,只用直尺(不带刻度)作图:
①如图2,在 ABCD中,E为CD的中点,作BC的中点F;
②图3,在由小正方形组成的网格中,的顶点都在小正方形的顶点上,作△ABC的高AH
五、综合题
13.⊙ 的两条弦 , 相交于点 .
(1)若 ,且 , ,求 的长.
(2)若AB是⊙O的直径,AB⊥CD,且AE=2,CD= 8 ,求⊙O的半径.
六、实践探究题
14.
(1)定义:有一组对角互余的四边形叫做对余四边形.理解:(1)若四边形ABCD是对余四边形,则∠A与∠C的度数之和为 .
(2)[证明]如图1,MN是⊙O的直径,点A,B,C在⊙O上,AM,CN相交于点D.求证:四边形 ABCD 是对余四边形.
(3)[探究]如图2,在对余四边形ABCD中,AB=BC,∠ABC=60°,探究线段AD,CD和BD之间有怎样的数量关系 写出猜想,并说明理由.
答案解析部分
1.【答案】D
【知识点】实数范围内分解因式;圆心角、弧、弦的关系
2.【答案】D
【知识点】勾股定理的应用;圆心角、弧、弦的关系
3.【答案】C
【知识点】圆心角、弧、弦的关系
4.【答案】A
【知识点】点到直线的距离;平行线的性质;三角形的面积;勾股定理;圆心角、弧、弦的关系
5.【答案】3
【知识点】圆心角、弧、弦的关系
6.【答案】35°
【知识点】圆心角、弧、弦的关系
7.【答案】2
【知识点】圆心角、弧、弦的关系
8.【答案】110°
【知识点】圆心角、弧、弦的关系
9.【答案】证明: ,
,
CD⊥OA于D,CE⊥OB于E,
∠CDO=∠CEO=90°,
在△ODC和△OEC中,
,
△ODC≌△OEC(AAS),
CD=CE.
【知识点】圆心角、弧、弦的关系
10.【答案】证明:∵BD=AC,
∴ ,
∴ = ,
即 ,
∴AB=CD.
【知识点】圆心角、弧、弦的关系
11.【答案】证明:连接AC,如图,
∵AB=CD,
∴.
∴.
即.
∴∠A=∠C.
∴PA=PC.
∴PA﹣AB=PC﹣CD.
即:PB=PD.
【知识点】圆心角、弧、弦的关系
12.【答案】(1)如图所示,四边形ABCD即为所求;
(2)①如图所示,点F即为所求;
②如图所示,AH即为所求.
【知识点】三角形的角平分线、中线和高;全等三角形的判定与性质;平行四边形的性质;圆心角、弧、弦的关系
13.【答案】(1)解:如图甲,当点 在 的左侧时,
∵ ,
∴
∴ .
∴ , .
如图乙,当点 在 的右侧时,
同理: .
(2)解:如图丙,若点 在 的下方,连结 C ,
∵ 是⊙ 的直径, ,
∴ ,
设 ,则 ,
∵ ,
∴ ,即 ,
解得 .
如图丁,若点 在 的上方,
则 ,与 矛盾,
∴⊙ 的半径为 .
【知识点】垂径定理;圆心角、弧、弦的关系
14.【答案】(1)90°或270°
(2)证明:∵MN是⊙O的直径,点A,B,C在⊙O上,
∴∠BAM+∠BCN=90°,
即∠BAD+∠BCD=90°,
∴四边形ABCD是对余四边形;
(3)解:线段AD,CD和BD之间数量关系为:AD2+CD2=BD2,理由如下:
∵四边形ABCD是对余四边形,∠ABC=60°,
∴∠ADC=30°,
∵AB=BC,
∴将△BCD绕点B逆时针旋转60°,得到△BAF,连接FD,如图3:
∴△BCD≌△BAF,∠FBD=60°,
∴BF=BD,∠BDC=∠BFA,
∴△BFD是等边三角形,
∴BF=BD=DF,
∵∠ADC=30°,
∴∠ADB+∠BDC=30°,
∴∠BFA+∠ADB=30°,
∵∠FBD+∠BFA+∠ADB+∠AFD+∠ADF=180°,
∴60°+30°+∠AFD+∠ADF=180°,
∴∠AFD+∠ADF=90°,
∴∠FAD=90°,
∴AD2+AF2=DF2,
∴AD2+CD2=BD2.
【知识点】等边三角形的判定与性质;勾股定理;多边形内角与外角;圆心角、弧、弦的关系;旋转的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
{浙教版九上同步练习}
5.4圆心角
一、单选题
1.下列语句中,其中正确的个数是( )
①将多项式a(x﹣y)2﹣b(y﹣x)因式分解,则原式=(x﹣y)(ax﹣ay+b);②将多项式x2+4y2﹣4xy因式分解,则原式=(x﹣2y)2;③90°的圆周角所对的弦是直径;④半圆(或直径)所对的圆周角是直角.
A.1 B.2 C.3 D.4
2.如图,在平面直角坐标系中,A(4,0),B(0,3),以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则点C坐标为( )
A.(1,0) B.(-5,0) C.(0,1) D.(-1,0)
3.如图、、是上的三点,是劣弧的中点,,则的度数等于( )
A. B. C. D.
4.如图,△ABC内接于圆O,AC=10,BC=24,且∠A=90°+∠B,则点O到AB的距离为( )
A. B. C.2.4 D.
二、填空题
5.如图,在⊙O中, ,AB=3,则AC= .
6.如图,已知AB,CD是⊙O的直径,CE是弦,且 , ,则∠BOE的度数 .
7.圆的一条弦把圆分为5:1两部分,如果圆的半径是2cm,则这条弦的长是 cm.
8.如图,已知点C是 的一点,圆周角∠ACB为125°,则圆心角∠AOB= 度.
三、解答题
9.如图: ,CD⊥OA于D,CE⊥OB于E,求证:CD=CE.
10.如图,点A,B,C,D在⊙O上,BD=AC.求证:AB=CD.
11.如图,⊙O的弦AB、CD的延长线相交于点P,且AB=CD,求证:PB=PD.
四、作图题
12.按要求作图,不要求写作法,但要保留作图痕迹.
(1)如图1,A为圆E上一点,请用直尺(不带刻度)和圆规作出圆内接正方形;
(2)我们知道,三角形具有性质,三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高交于同一点,请运用上述性质,只用直尺(不带刻度)作图:
①如图2,在 ABCD中,E为CD的中点,作BC的中点F;
②图3,在由小正方形组成的网格中,的顶点都在小正方形的顶点上,作△ABC的高AH
五、综合题
13.⊙ 的两条弦 , 相交于点 .
(1)若 ,且 , ,求 的长.
(2)若AB是⊙O的直径,AB⊥CD,且AE=2,CD= 8 ,求⊙O的半径.
六、实践探究题
14.
(1)定义:有一组对角互余的四边形叫做对余四边形.理解:(1)若四边形ABCD是对余四边形,则∠A与∠C的度数之和为 .
(2)[证明]如图1,MN是⊙O的直径,点A,B,C在⊙O上,AM,CN相交于点D.求证:四边形 ABCD 是对余四边形.
(3)[探究]如图2,在对余四边形ABCD中,AB=BC,∠ABC=60°,探究线段AD,CD和BD之间有怎样的数量关系 写出猜想,并说明理由.
答案解析部分
1.【答案】D
【知识点】实数范围内分解因式;圆心角、弧、弦的关系
2.【答案】D
【知识点】勾股定理的应用;圆心角、弧、弦的关系
3.【答案】C
【知识点】圆心角、弧、弦的关系
4.【答案】A
【知识点】点到直线的距离;平行线的性质;三角形的面积;勾股定理;圆心角、弧、弦的关系
5.【答案】3
【知识点】圆心角、弧、弦的关系
6.【答案】35°
【知识点】圆心角、弧、弦的关系
7.【答案】2
【知识点】圆心角、弧、弦的关系
8.【答案】110°
【知识点】圆心角、弧、弦的关系
9.【答案】证明: ,
,
CD⊥OA于D,CE⊥OB于E,
∠CDO=∠CEO=90°,
在△ODC和△OEC中,
,
△ODC≌△OEC(AAS),
CD=CE.
【知识点】圆心角、弧、弦的关系
10.【答案】证明:∵BD=AC,
∴ ,
∴ = ,
即 ,
∴AB=CD.
【知识点】圆心角、弧、弦的关系
11.【答案】证明:连接AC,如图,
∵AB=CD,
∴.
∴.
即.
∴∠A=∠C.
∴PA=PC.
∴PA﹣AB=PC﹣CD.
即:PB=PD.
【知识点】圆心角、弧、弦的关系
12.【答案】(1)如图所示,四边形ABCD即为所求;
(2)①如图所示,点F即为所求;
②如图所示,AH即为所求.
【知识点】三角形的角平分线、中线和高;全等三角形的判定与性质;平行四边形的性质;圆心角、弧、弦的关系
13.【答案】(1)解:如图甲,当点 在 的左侧时,
∵ ,
∴
∴ .
∴ , .
如图乙,当点 在 的右侧时,
同理: .
(2)解:如图丙,若点 在 的下方,连结 C ,
∵ 是⊙ 的直径, ,
∴ ,
设 ,则 ,
∵ ,
∴ ,即 ,
解得 .
如图丁,若点 在 的上方,
则 ,与 矛盾,
∴⊙ 的半径为 .
【知识点】垂径定理;圆心角、弧、弦的关系
14.【答案】(1)90°或270°
(2)证明:∵MN是⊙O的直径,点A,B,C在⊙O上,
∴∠BAM+∠BCN=90°,
即∠BAD+∠BCD=90°,
∴四边形ABCD是对余四边形;
(3)解:线段AD,CD和BD之间数量关系为:AD2+CD2=BD2,理由如下:
∵四边形ABCD是对余四边形,∠ABC=60°,
∴∠ADC=30°,
∵AB=BC,
∴将△BCD绕点B逆时针旋转60°,得到△BAF,连接FD,如图3:
∴△BCD≌△BAF,∠FBD=60°,
∴BF=BD,∠BDC=∠BFA,
∴△BFD是等边三角形,
∴BF=BD=DF,
∵∠ADC=30°,
∴∠ADB+∠BDC=30°,
∴∠BFA+∠ADB=30°,
∵∠FBD+∠BFA+∠ADB+∠AFD+∠ADF=180°,
∴60°+30°+∠AFD+∠ADF=180°,
∴∠AFD+∠ADF=90°,
∴∠FAD=90°,
∴AD2+AF2=DF2,
∴AD2+CD2=BD2.
【知识点】等边三角形的判定与性质;勾股定理;多边形内角与外角;圆心角、弧、弦的关系;旋转的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
