{浙教版九上同步练习} 3.6 圆内接四边形(含答案)
文档属性
| 名称 | {浙教版九上同步练习} 3.6 圆内接四边形(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 15:46:28 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
{浙教版九上同步练习}
3.5圆内接四边形
一、单选题
1.圆内接四边形ABCD中,若∠A∶∠B∶∠C=1∶2∶3,则∠D的度数是( )
A.45° B.60° C.90° D.135°
2.下列有关圆的一些结论:①任意三点确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦;并且平分弦所对的弧,④圆内接四边形对角互补.其中错误的结论有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在⊙O中,圆心角∠AOB=120°,P为弧AB上一点,则∠APB度数是( )
A.100° B.110° C.120° D.130°
4.在圆内接四边形ABCD中,∠A∶∠B∶∠C∶∠D的度数之比可能是( )
A.1∶2∶3∶4 B.4∶2∶1∶3 C.4∶2∶3∶1 D.1∶3∶2∶4
5.如图,四边形 是半圆的内接四边形, 是直径, .若 ,则 的度数等于( )
A. B. C. D.
6.如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( )
A.∠OBA=∠OCA B.四边形OABC内接于⊙O
C.AB=2BC D.∠OBA+∠BOC=90°
二、填空题
7.圆内接四边形的对角 .如果一个平行四边形内接于圆,它必定是 。
8.圆内接四边形ABCD中,∠A:∠B:∠C:∠D=3:5:6:m,则m= ,∠D= .
9.如图,四边形 内接于 ,若 ,则 的度数为 °.
10.如图,A,B,C,D是⊙O上的四个点,∠C=110°,则∠BOD= 度.
三、解答题
11.已知在△ABC中,AB=AC,以AB为直径的⊙O分别交AC于点 D,BC于点E,连接ED.求证:ED=EC.
12.如图所示,四边形ABCD是的内接四边形,,.求:
(1)的度数.
(2)CD的长.
13.如图③,点E,D分别是正三角形ABC,正四边形ABCM,正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点,且△ABE与△BCD能相互重合,DB的延长线交AE于点F.
(1)在图①中,求∠AFB的度数
(2)在图②中,∠AFB的度数为 度,图③中,∠AFB的度数为 度
(3)继续探索,可将本题推广到一般的正n边形情况,用含n的式子表示∠AFB的度数.
四、作图题
14.如图,在5×5的网格中,按下列要求作图.
(1)在图1中作出,使得.
(2)在图2中作出,使得.
五、综合题
15.如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
(1)求证:∠A=∠AEB
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形
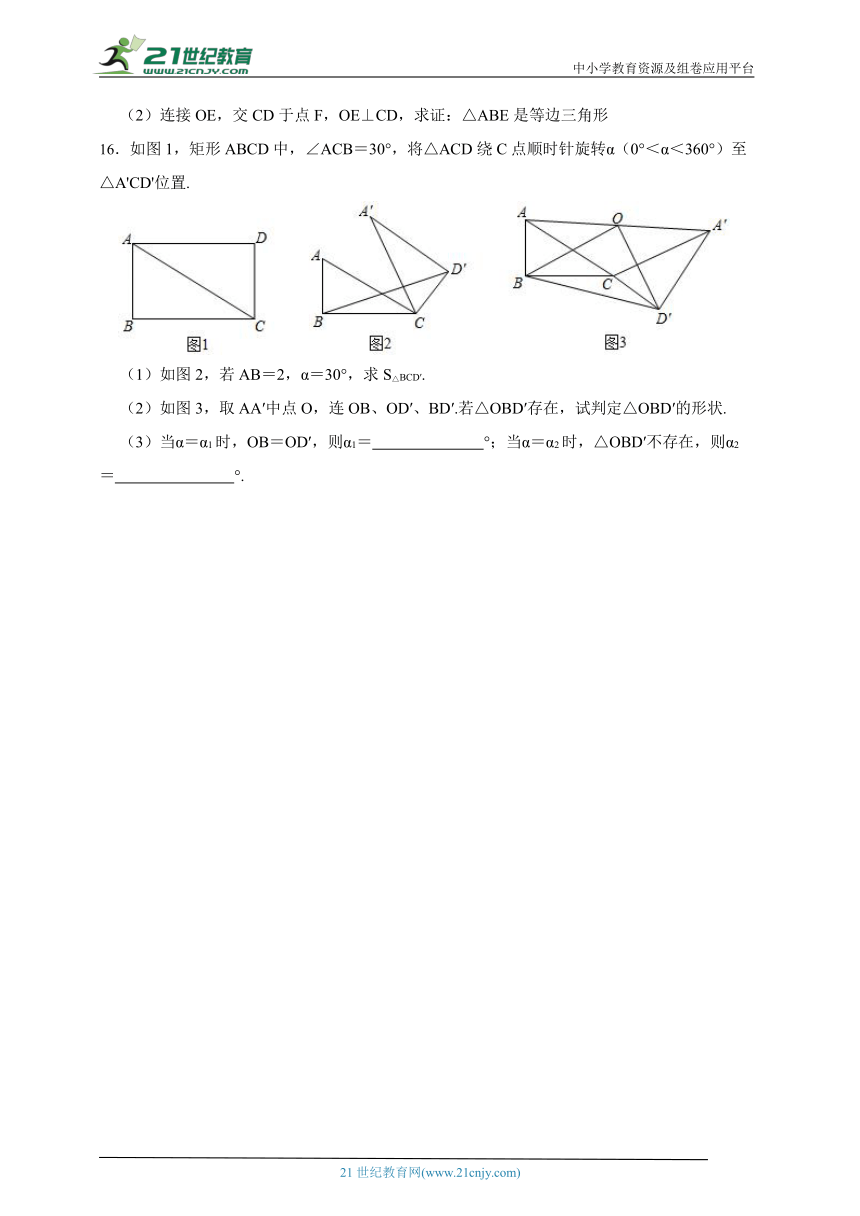
16.如图1,矩形ABCD中,∠ACB=30°,将△ACD绕C点顺时针旋转α(0°<α<360°)至△A'CD'位置.
(1)如图2,若AB=2,α=30°,求S△BCD′.
(2)如图3,取AA′中点O,连OB、OD′、BD′.若△OBD′存在,试判定△OBD′的形状.
(3)当α=α1时,OB=OD′,则α1= °;当α=α2时,△OBD′不存在,则α2= °.
答案解析部分
1.【答案】C
【知识点】圆内接四边形的性质
2.【答案】C
【知识点】垂径定理;圆周角定理;圆内接四边形的性质;确定圆的条件
3.【答案】C
【知识点】圆周角定理;圆内接四边形的性质
4.【答案】B
【知识点】圆内接四边形的性质
5.【答案】A
【知识点】圆周角定理;圆内接四边形的性质
6.【答案】D
【知识点】垂径定理的应用;圆心角、弧、弦的关系;圆内接四边形的性质
7.【答案】互补;矩形
【知识点】圆内接四边形的性质
8.【答案】4;80°
【知识点】圆内接四边形的性质
9.【答案】140
【知识点】圆周角定理;圆内接四边形的性质
10.【答案】140
【知识点】圆周角定理;圆内接四边形的性质
11.【答案】解:∵AB=AC,
∴∠B=∠C,
∵四边形ABED是圆内接四边形,
∴∠CDE=∠B,
∴∠CDE=∠C,
∴CE=DE.
【知识点】等腰三角形的判定与性质;圆内接四边形的性质
12.【答案】(1)解:四边形ABCD是的内接四边形,
,
;
(2)解:如图所示,连结BD.
在Rt中,
由勾股定理得.
在Rt△BCD中,,
.
【知识点】含30°角的直角三角形;勾股定理;圆周角定理;圆内接四边形的性质
13.【答案】(1)解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠ACB=60°,
∴∠ABE=∠BCD=120°.
∵△ABE与△BCD能相互重合,
∴∠E=∠D,∠DBC=∠BAE.
∵∠FBE=∠CBD,
∴∠AFB=∠E+∠FBE=∠D+∠CBD=∠ACB=60°
(2)90;108
(3)解:由(1)(2)可知,在正n边形中,∠AFB=
【知识点】圆内接四边形的性质
14.【答案】(1)解:如图,即为所求;
(2)解:如图,即为所求;
【知识点】平行线的性质;圆周角定理;圆内接四边形的性质
15.【答案】(1)证明:∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠A=∠DCE,
∵DC=DE,
∴∠DCE=∠AEB,
∴∠A=∠AEB
(2)证明:∵∠A=∠AEB,
∴△ABE是等腰三角形,
∵EO⊥CD,
∴CF=DF,
∴EO是CD的垂直平分线,
∴ED=EC,
∵DC=DE,
∴DC=DE=EC,
∴△DCE是等边三角形,
∴∠AEB=60°,
∴△ABE是等边三角形.
【知识点】等边三角形的判定与性质;圆周角定理;圆内接四边形的性质
16.【答案】(1)解:作D'E⊥BC交BC的延长线于E,如图2所示:
则∠E=90°,
∵四边形ABCD是矩形,
∴∠ABC=90°,AB∥CD,AD∥BC,CD=AB=2,
∴∠ACD=∠BAC,∠DAC=∠ACB=30°,
∵∠ACB=30°,
∴BC= AB=2 ,∠ACD=∠BAC=60°,
由旋转的性质得:CD'=CD=2,∠ACA'=30°,
∴∠D'CE ,
∴∠CD'E ,
∴CE= CD'=1,D'E= CE= ,
∴S△BCD′= BC×D'E= ×2 × =3;
(2)解:△OBD′是直角三角形,理由如下:
连接OC,如图3所示:
由旋转的性质得:CA'=CA,∠A'D'C=∠ADC=90°,∠D'A'C=∠DAC=30°,
∵O是AA′的中点,
∴OC⊥AA',
∴∠AOC=∠A'OC= =∠ABC=∠A'D'C,
∴∠ABC+∠AOC=180°,
∴A、B、C、O四点共圆,
∴∠BOC=∠BAC=60°,
同理;A'、D'、C、O四点共圆,
∴∠D'OC=∠D'A'C=30°,
∴∠BOD'=90°,
∴△BOD'是直角三角形;
(3)90°或270;240°或300
【知识点】矩形的性质;圆周角定理;圆内接四边形的性质;旋转的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
{浙教版九上同步练习}
3.5圆内接四边形
一、单选题
1.圆内接四边形ABCD中,若∠A∶∠B∶∠C=1∶2∶3,则∠D的度数是( )
A.45° B.60° C.90° D.135°
2.下列有关圆的一些结论:①任意三点确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦;并且平分弦所对的弧,④圆内接四边形对角互补.其中错误的结论有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在⊙O中,圆心角∠AOB=120°,P为弧AB上一点,则∠APB度数是( )
A.100° B.110° C.120° D.130°
4.在圆内接四边形ABCD中,∠A∶∠B∶∠C∶∠D的度数之比可能是( )
A.1∶2∶3∶4 B.4∶2∶1∶3 C.4∶2∶3∶1 D.1∶3∶2∶4
5.如图,四边形 是半圆的内接四边形, 是直径, .若 ,则 的度数等于( )
A. B. C. D.
6.如图,A,B,C是⊙O上三个点,∠AOB=2∠BOC,则下列说法中正确的是( )
A.∠OBA=∠OCA B.四边形OABC内接于⊙O
C.AB=2BC D.∠OBA+∠BOC=90°
二、填空题
7.圆内接四边形的对角 .如果一个平行四边形内接于圆,它必定是 。
8.圆内接四边形ABCD中,∠A:∠B:∠C:∠D=3:5:6:m,则m= ,∠D= .
9.如图,四边形 内接于 ,若 ,则 的度数为 °.
10.如图,A,B,C,D是⊙O上的四个点,∠C=110°,则∠BOD= 度.
三、解答题
11.已知在△ABC中,AB=AC,以AB为直径的⊙O分别交AC于点 D,BC于点E,连接ED.求证:ED=EC.
12.如图所示,四边形ABCD是的内接四边形,,.求:
(1)的度数.
(2)CD的长.
13.如图③,点E,D分别是正三角形ABC,正四边形ABCM,正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点,且△ABE与△BCD能相互重合,DB的延长线交AE于点F.
(1)在图①中,求∠AFB的度数
(2)在图②中,∠AFB的度数为 度,图③中,∠AFB的度数为 度
(3)继续探索,可将本题推广到一般的正n边形情况,用含n的式子表示∠AFB的度数.
四、作图题
14.如图,在5×5的网格中,按下列要求作图.
(1)在图1中作出,使得.
(2)在图2中作出,使得.
五、综合题
15.如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
(1)求证:∠A=∠AEB
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形
16.如图1,矩形ABCD中,∠ACB=30°,将△ACD绕C点顺时针旋转α(0°<α<360°)至△A'CD'位置.
(1)如图2,若AB=2,α=30°,求S△BCD′.
(2)如图3,取AA′中点O,连OB、OD′、BD′.若△OBD′存在,试判定△OBD′的形状.
(3)当α=α1时,OB=OD′,则α1= °;当α=α2时,△OBD′不存在,则α2= °.
答案解析部分
1.【答案】C
【知识点】圆内接四边形的性质
2.【答案】C
【知识点】垂径定理;圆周角定理;圆内接四边形的性质;确定圆的条件
3.【答案】C
【知识点】圆周角定理;圆内接四边形的性质
4.【答案】B
【知识点】圆内接四边形的性质
5.【答案】A
【知识点】圆周角定理;圆内接四边形的性质
6.【答案】D
【知识点】垂径定理的应用;圆心角、弧、弦的关系;圆内接四边形的性质
7.【答案】互补;矩形
【知识点】圆内接四边形的性质
8.【答案】4;80°
【知识点】圆内接四边形的性质
9.【答案】140
【知识点】圆周角定理;圆内接四边形的性质
10.【答案】140
【知识点】圆周角定理;圆内接四边形的性质
11.【答案】解:∵AB=AC,
∴∠B=∠C,
∵四边形ABED是圆内接四边形,
∴∠CDE=∠B,
∴∠CDE=∠C,
∴CE=DE.
【知识点】等腰三角形的判定与性质;圆内接四边形的性质
12.【答案】(1)解:四边形ABCD是的内接四边形,
,
;
(2)解:如图所示,连结BD.
在Rt中,
由勾股定理得.
在Rt△BCD中,,
.
【知识点】含30°角的直角三角形;勾股定理;圆周角定理;圆内接四边形的性质
13.【答案】(1)解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠ACB=60°,
∴∠ABE=∠BCD=120°.
∵△ABE与△BCD能相互重合,
∴∠E=∠D,∠DBC=∠BAE.
∵∠FBE=∠CBD,
∴∠AFB=∠E+∠FBE=∠D+∠CBD=∠ACB=60°
(2)90;108
(3)解:由(1)(2)可知,在正n边形中,∠AFB=
【知识点】圆内接四边形的性质
14.【答案】(1)解:如图,即为所求;
(2)解:如图,即为所求;
【知识点】平行线的性质;圆周角定理;圆内接四边形的性质
15.【答案】(1)证明:∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠A=∠DCE,
∵DC=DE,
∴∠DCE=∠AEB,
∴∠A=∠AEB
(2)证明:∵∠A=∠AEB,
∴△ABE是等腰三角形,
∵EO⊥CD,
∴CF=DF,
∴EO是CD的垂直平分线,
∴ED=EC,
∵DC=DE,
∴DC=DE=EC,
∴△DCE是等边三角形,
∴∠AEB=60°,
∴△ABE是等边三角形.
【知识点】等边三角形的判定与性质;圆周角定理;圆内接四边形的性质
16.【答案】(1)解:作D'E⊥BC交BC的延长线于E,如图2所示:
则∠E=90°,
∵四边形ABCD是矩形,
∴∠ABC=90°,AB∥CD,AD∥BC,CD=AB=2,
∴∠ACD=∠BAC,∠DAC=∠ACB=30°,
∵∠ACB=30°,
∴BC= AB=2 ,∠ACD=∠BAC=60°,
由旋转的性质得:CD'=CD=2,∠ACA'=30°,
∴∠D'CE ,
∴∠CD'E ,
∴CE= CD'=1,D'E= CE= ,
∴S△BCD′= BC×D'E= ×2 × =3;
(2)解:△OBD′是直角三角形,理由如下:
连接OC,如图3所示:
由旋转的性质得:CA'=CA,∠A'D'C=∠ADC=90°,∠D'A'C=∠DAC=30°,
∵O是AA′的中点,
∴OC⊥AA',
∴∠AOC=∠A'OC= =∠ABC=∠A'D'C,
∴∠ABC+∠AOC=180°,
∴A、B、C、O四点共圆,
∴∠BOC=∠BAC=60°,
同理;A'、D'、C、O四点共圆,
∴∠D'OC=∠D'A'C=30°,
∴∠BOD'=90°,
∴△BOD'是直角三角形;
(3)90°或270;240°或300
【知识点】矩形的性质;圆周角定理;圆内接四边形的性质;旋转的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
