{浙教版九上同步练习} 3.7 正多边形(含答案)
文档属性
| 名称 | {浙教版九上同步练习} 3.7 正多边形(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 17:54:52 | ||
图片预览

文档简介
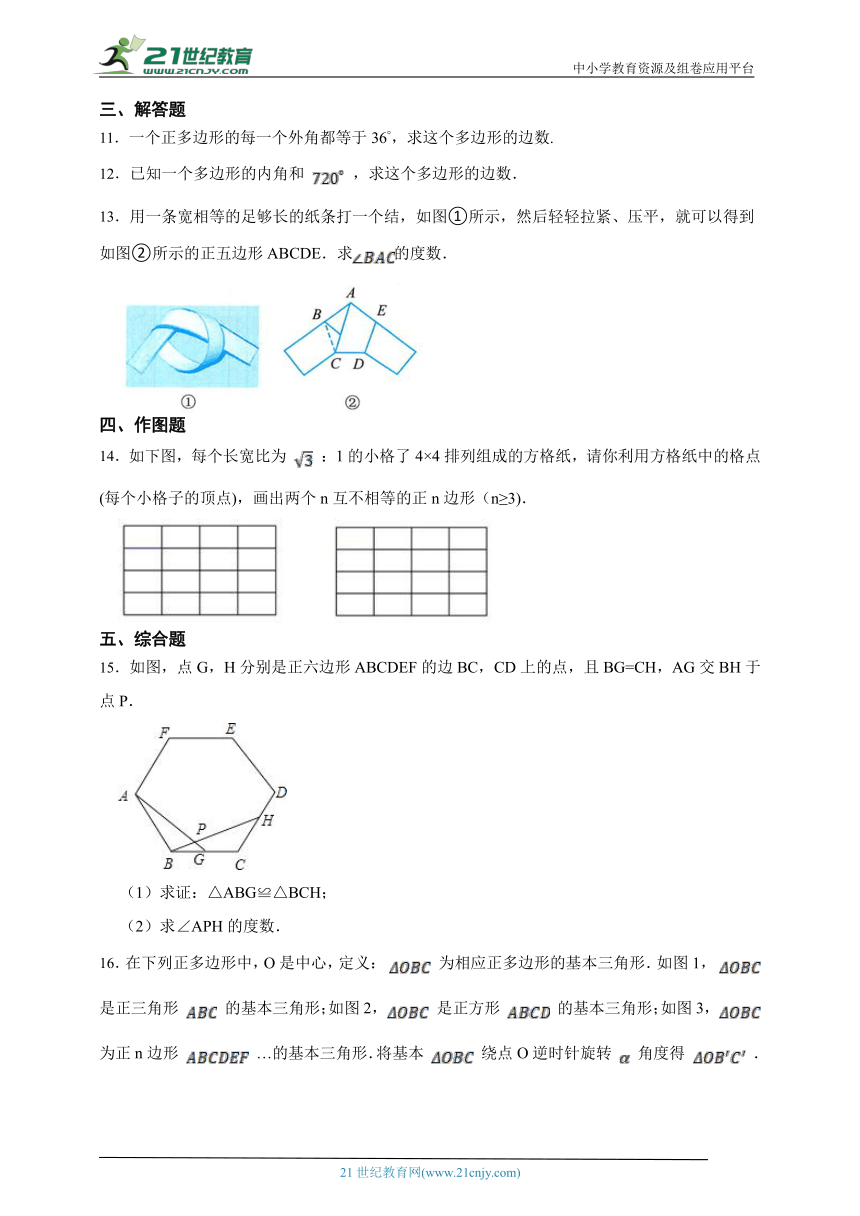
中小学教育资源及组卷应用平台
{浙教版九上同步练习} 3.7正多边形
一、单选题
1.若正多边形的一个外角是60°,则该正多边形的边数是( )
A.4 B.5 C.6 D.7
2.若正六边形的边长为6,则其外接圆半径为( )
A.3 B.3 C.3 D.6
3.如果一个正多边形的一个内角是144°,则这个多边形是( )
A.正十边形 B.正九边形 C.正八边形 D.正七边形
4.一个正六边形的内角和的度数为( )
A.1080° B.720° C.540° D.360°
5.如图,在边长为a的正六边形内有两个小三角形,相关数据如图所示.若图中阴影部分的面积为S1,两个空白三角形的面积为S2.则 =( )
A.3 B.4 C.5 D.6
6.正六边形的半径与边心距之比为( )
A.1: B. :1 C. :2 D.2:
二、填空题
7.已知一个正多边形内角的度数为108°,则它的边数为 .
8.多边形是由一些 组成的封闭图形.
9.正十边形的中心角等于 度.
10.剪纸是中国最古老的民间艺术之一.如图,这个剪纸图案绕着它的中心旋转角α (0°<α<360°)后能够与它本身完全重合.则角α可以为 度(写出一个即可).
三、解答题
11.一个正多边形的每一个外角都等于36°,求这个多边形的边数.
12.已知一个多边形的内角和 ,求这个多边形的边数.
13.用一条宽相等的足够长的纸条打一个结,如图①所示,然后轻轻拉紧、压平,就可以得到如图②所示的正五边形ABCDE.求的度数.
四、作图题
14.如下图,每个长宽比为 :1的小格了4×4排列组成的方格纸,请你利用方格纸中的格点(每个小格子的顶点),画出两个n互不相等的正n边形(n≥3).
五、综合题
15.如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.
(1)求证:△ABG≌△BCH;
(2)求∠APH的度数.
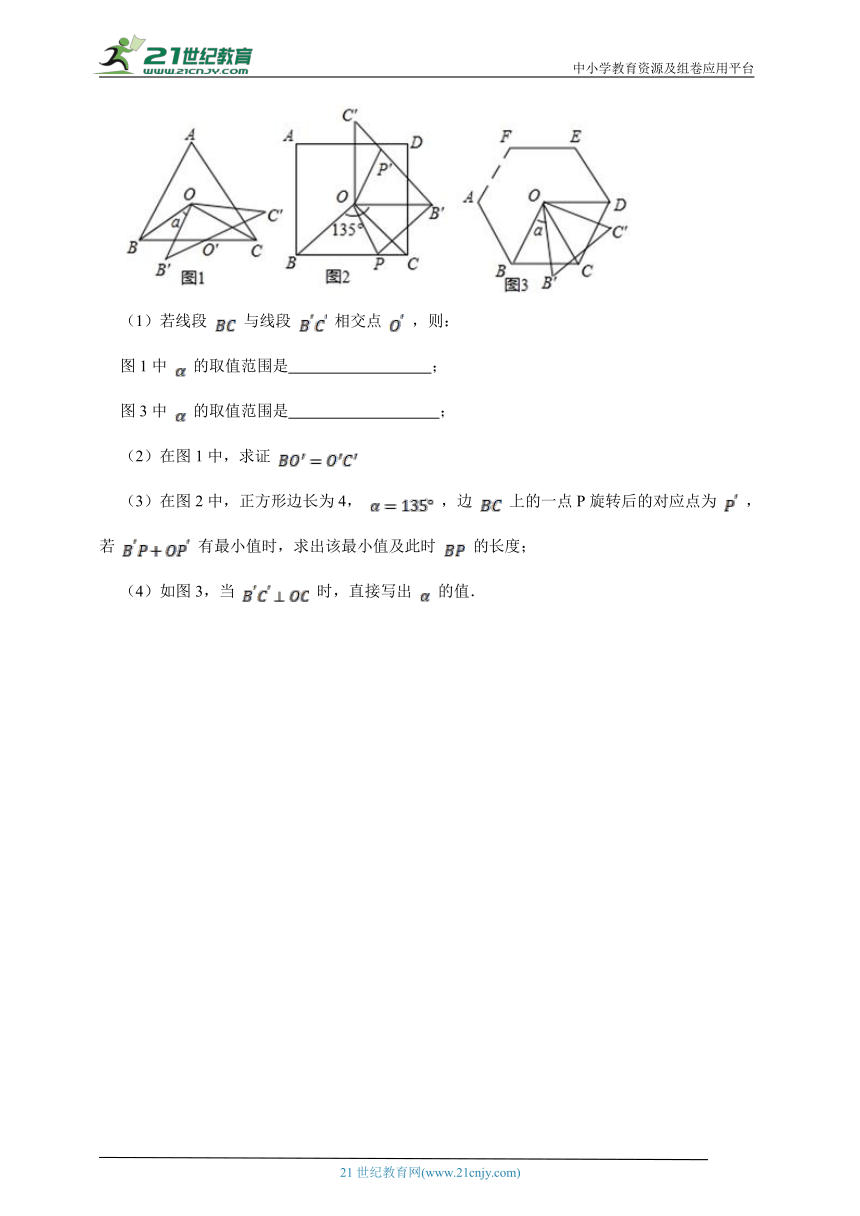
16.在下列正多边形中,O是中心,定义: 为相应正多边形的基本三角形.如图1, 是正三角形 的基本三角形;如图2, 是正方形 的基本三角形;如图3, 为正n边形 …的基本三角形.将基本 绕点O逆时针旋转 角度得 .
(1)若线段 与线段 相交点 ,则:
图1中 的取值范围是 ;
图3中 的取值范围是 ;
(2)在图1中,求证
(3)在图2中,正方形边长为4, ,边 上的一点P旋转后的对应点为 ,若 有最小值时,求出该最小值及此时 的长度;
(4)如图3,当 时,直接写出 的值.
答案解析部分
1.【答案】C
【知识点】多边形内角与外角;正多边形的性质
2.【答案】D
【知识点】圆内接正多边形
3.【答案】A
【知识点】正多边形的性质
4.【答案】B
【知识点】正多边形的性质
5.【答案】C
【知识点】三角形的面积;正多边形的性质
6.【答案】D
【知识点】圆内接正多边形;正多边形的性质
7.【答案】5
【知识点】正多边形的性质
8.【答案】不在同一条直线上线段依次首尾相连
【知识点】圆内接正多边形
9.【答案】36
【知识点】多边形内角与外角;圆心角、弧、弦的关系;正多边形的性质
10.【答案】60
【知识点】正多边形的性质
11.【答案】解:解:∵一个正多边形的每个外角都等于36°,
∴这个多边形的边数为360°÷36°=10.
【知识点】正多边形的性质
12.【答案】解:设这个多边形的边数是n,
依题意得 ,
,
.
答:这个多边形的边数是6.
【知识点】多边形内角与外角;正多边形的性质
13.【答案】解:∵正五边形ABCDE ,
∴∠ABC=(5-2)×180°÷5=108°,AB=BC,
∴∠BAC=(180°-108°)÷2=36°.
【知识点】三角形内角和定理;等腰三角形的性质;多边形内角与外角;正多边形的性质
14.【答案】 解:如图所示,构造一个正方形和正六边形,
由勾股定理得,正方形的边长为,
正六边形的每条边长为 .
【知识点】勾股定理;正多边形的性质
15.【答案】(1)解:∵在正六边形ABCDEF中,AB=BC,∠ABC=∠C=120°,在△ABG与△BCH中AB=BC,∠ABC=∠C=120°, BG=CH ,
∴△ABG≌△BCH
(2)解:由(1)知:△ABG≌△BCH,∴∠BAG=∠HBC,
∴∠BPG=∠ABG=120°,
∴∠APH=∠BPG=120°
【知识点】全等三角形的判定与性质;正多边形的性质
16.【答案】(1);
(2)证明:如图1中,作OE⊥BC于E,OF⊥ 于F,连接 .
∵∠OEB=∠OF =90°,
根据题意,O是中心,∴OB=OC,
∴∠OBE=∠ ,
∴△OBE≌△O F(AAS),
∴OE=OF,BE= F
∵ ,
∴Rt△ ≌Rt△ (HL),
∴ ,
∴ .
(3)解:如图2中,作点O关于BC的对称点E,连接OE交BC于K,连接 交BC于点 ,连接 ,此时 的值最小.
∵∠ =135°,∠BOC=90°,
∴∠OCB=∠ =45°,
∴ ∥BC,
∵OK⊥BC,OB=OC,
∴BK=CK=2,OB=2 ,
∵ ∥ ,OK=KE,
∴ ,
∴ = = ,
∴ =2+ ,
在Rt△ 中, = .
∵ ,
∴ 有最小值,最小值为 ,此时 =2+ .
(4)
【知识点】三角形全等的判定;旋转的性质;正多边形的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
{浙教版九上同步练习} 3.7正多边形
一、单选题
1.若正多边形的一个外角是60°,则该正多边形的边数是( )
A.4 B.5 C.6 D.7
2.若正六边形的边长为6,则其外接圆半径为( )
A.3 B.3 C.3 D.6
3.如果一个正多边形的一个内角是144°,则这个多边形是( )
A.正十边形 B.正九边形 C.正八边形 D.正七边形
4.一个正六边形的内角和的度数为( )
A.1080° B.720° C.540° D.360°
5.如图,在边长为a的正六边形内有两个小三角形,相关数据如图所示.若图中阴影部分的面积为S1,两个空白三角形的面积为S2.则 =( )
A.3 B.4 C.5 D.6
6.正六边形的半径与边心距之比为( )
A.1: B. :1 C. :2 D.2:
二、填空题
7.已知一个正多边形内角的度数为108°,则它的边数为 .
8.多边形是由一些 组成的封闭图形.
9.正十边形的中心角等于 度.
10.剪纸是中国最古老的民间艺术之一.如图,这个剪纸图案绕着它的中心旋转角α (0°<α<360°)后能够与它本身完全重合.则角α可以为 度(写出一个即可).
三、解答题
11.一个正多边形的每一个外角都等于36°,求这个多边形的边数.
12.已知一个多边形的内角和 ,求这个多边形的边数.
13.用一条宽相等的足够长的纸条打一个结,如图①所示,然后轻轻拉紧、压平,就可以得到如图②所示的正五边形ABCDE.求的度数.
四、作图题
14.如下图,每个长宽比为 :1的小格了4×4排列组成的方格纸,请你利用方格纸中的格点(每个小格子的顶点),画出两个n互不相等的正n边形(n≥3).
五、综合题
15.如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.
(1)求证:△ABG≌△BCH;
(2)求∠APH的度数.
16.在下列正多边形中,O是中心,定义: 为相应正多边形的基本三角形.如图1, 是正三角形 的基本三角形;如图2, 是正方形 的基本三角形;如图3, 为正n边形 …的基本三角形.将基本 绕点O逆时针旋转 角度得 .
(1)若线段 与线段 相交点 ,则:
图1中 的取值范围是 ;
图3中 的取值范围是 ;
(2)在图1中,求证
(3)在图2中,正方形边长为4, ,边 上的一点P旋转后的对应点为 ,若 有最小值时,求出该最小值及此时 的长度;
(4)如图3,当 时,直接写出 的值.
答案解析部分
1.【答案】C
【知识点】多边形内角与外角;正多边形的性质
2.【答案】D
【知识点】圆内接正多边形
3.【答案】A
【知识点】正多边形的性质
4.【答案】B
【知识点】正多边形的性质
5.【答案】C
【知识点】三角形的面积;正多边形的性质
6.【答案】D
【知识点】圆内接正多边形;正多边形的性质
7.【答案】5
【知识点】正多边形的性质
8.【答案】不在同一条直线上线段依次首尾相连
【知识点】圆内接正多边形
9.【答案】36
【知识点】多边形内角与外角;圆心角、弧、弦的关系;正多边形的性质
10.【答案】60
【知识点】正多边形的性质
11.【答案】解:解:∵一个正多边形的每个外角都等于36°,
∴这个多边形的边数为360°÷36°=10.
【知识点】正多边形的性质
12.【答案】解:设这个多边形的边数是n,
依题意得 ,
,
.
答:这个多边形的边数是6.
【知识点】多边形内角与外角;正多边形的性质
13.【答案】解:∵正五边形ABCDE ,
∴∠ABC=(5-2)×180°÷5=108°,AB=BC,
∴∠BAC=(180°-108°)÷2=36°.
【知识点】三角形内角和定理;等腰三角形的性质;多边形内角与外角;正多边形的性质
14.【答案】 解:如图所示,构造一个正方形和正六边形,
由勾股定理得,正方形的边长为,
正六边形的每条边长为 .
【知识点】勾股定理;正多边形的性质
15.【答案】(1)解:∵在正六边形ABCDEF中,AB=BC,∠ABC=∠C=120°,在△ABG与△BCH中AB=BC,∠ABC=∠C=120°, BG=CH ,
∴△ABG≌△BCH
(2)解:由(1)知:△ABG≌△BCH,∴∠BAG=∠HBC,
∴∠BPG=∠ABG=120°,
∴∠APH=∠BPG=120°
【知识点】全等三角形的判定与性质;正多边形的性质
16.【答案】(1);
(2)证明:如图1中,作OE⊥BC于E,OF⊥ 于F,连接 .
∵∠OEB=∠OF =90°,
根据题意,O是中心,∴OB=OC,
∴∠OBE=∠ ,
∴△OBE≌△O F(AAS),
∴OE=OF,BE= F
∵ ,
∴Rt△ ≌Rt△ (HL),
∴ ,
∴ .
(3)解:如图2中,作点O关于BC的对称点E,连接OE交BC于K,连接 交BC于点 ,连接 ,此时 的值最小.
∵∠ =135°,∠BOC=90°,
∴∠OCB=∠ =45°,
∴ ∥BC,
∵OK⊥BC,OB=OC,
∴BK=CK=2,OB=2 ,
∵ ∥ ,OK=KE,
∴ ,
∴ = = ,
∴ =2+ ,
在Rt△ 中, = .
∵ ,
∴ 有最小值,最小值为 ,此时 =2+ .
(4)
【知识点】三角形全等的判定;旋转的性质;正多边形的性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
