{浙教版九上同步练习} 第三章 圆的基本性质(基础知识)检测题(含答案)
文档属性
| 名称 | {浙教版九上同步练习} 第三章 圆的基本性质(基础知识)检测题(含答案) | 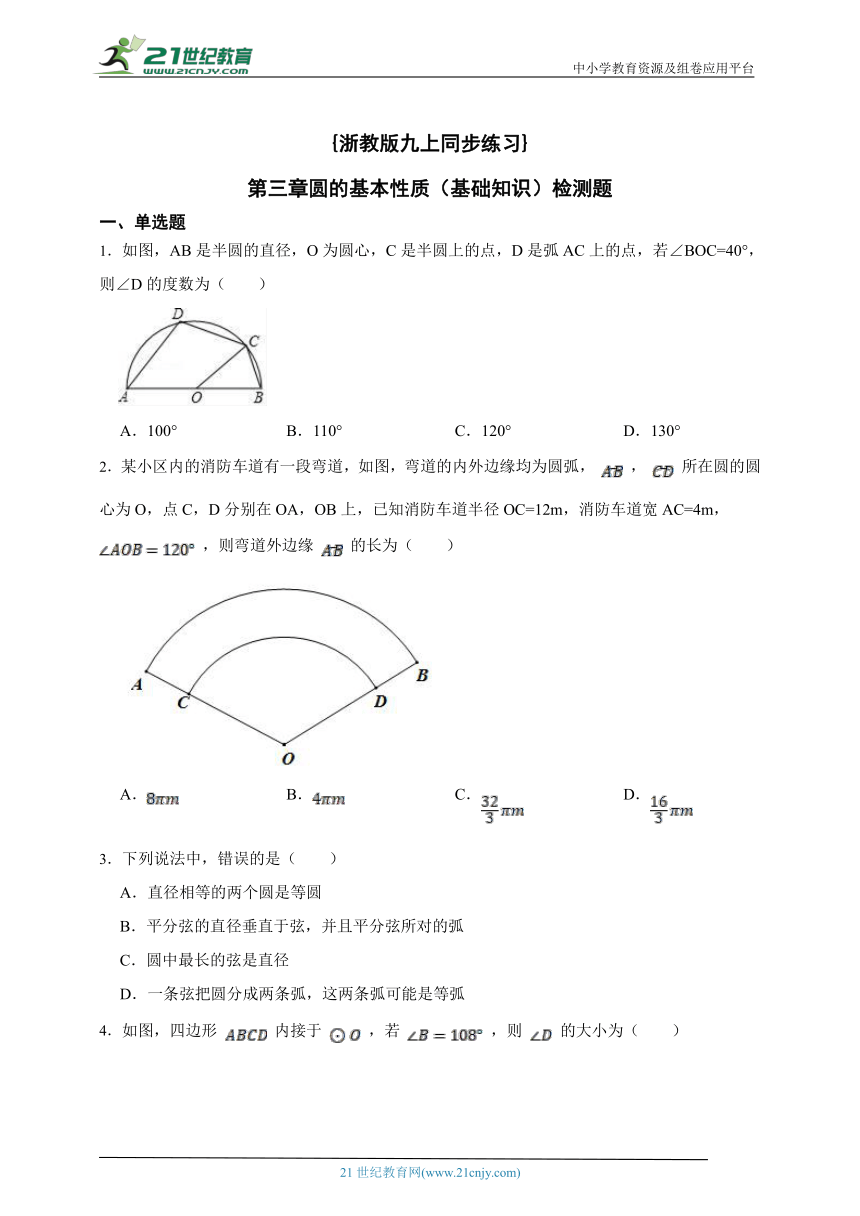 | |
| 格式 | doc | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 17:57:08 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
{浙教版九上同步练习}
第三章圆的基本性质(基础知识)检测题
一、单选题
1.如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是弧AC上的点,若∠BOC=40°,则∠D的度数为( )
A.100° B.110° C.120° D.130°
2.某小区内的消防车道有一段弯道,如图,弯道的内外边缘均为圆弧, , 所在圆的圆心为O,点C,D分别在OA,OB上,已知消防车道半径OC=12m,消防车道宽AC=4m, ,则弯道外边缘 的长为( )
A. B. C. D.
3.下列说法中,错误的是( )
A.直径相等的两个圆是等圆
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.圆中最长的弦是直径
D.一条弦把圆分成两条弧,这两条弧可能是等弧
4.如图,四边形 内接于 ,若 ,则 的大小为( )
A.36° B.54° C.62° D.72°
5.已知的半径为2,若,则点P与的位置关系是( )
A.点P在上 B.点P在内 C.点P在外 D.无法判断
6.已知方程x2-7x+12=0的两根恰好是一个直角三角形的两条直角边的长,则这个直角三角形的外接圆的直径为( )
A.2.5 B.6 C.5 D.
二、填空题
7.在一个圆中60度的圆心角所对的弧长为 ,则该圆的直径为
8.一个扇形的圆心角为135°,弧长为3πcm,则此扇形的面积是 cm2.
9.已知如图,在⊙O中,弦AB的长为8,圆心O到AB的距离为3.若点P是AB上的一动点,则OP的取值范围是 .
10.如图,AC为⊙O的直径,点B在圆上,OD⊥AC交⊙O于点D,连接BD,∠BDO=15°,则∠ACB= .
11.如图,AB为⊙O直径,点C、D在⊙O上,已知∠AOD=50°,AD∥OC,则∠BOC= 度.
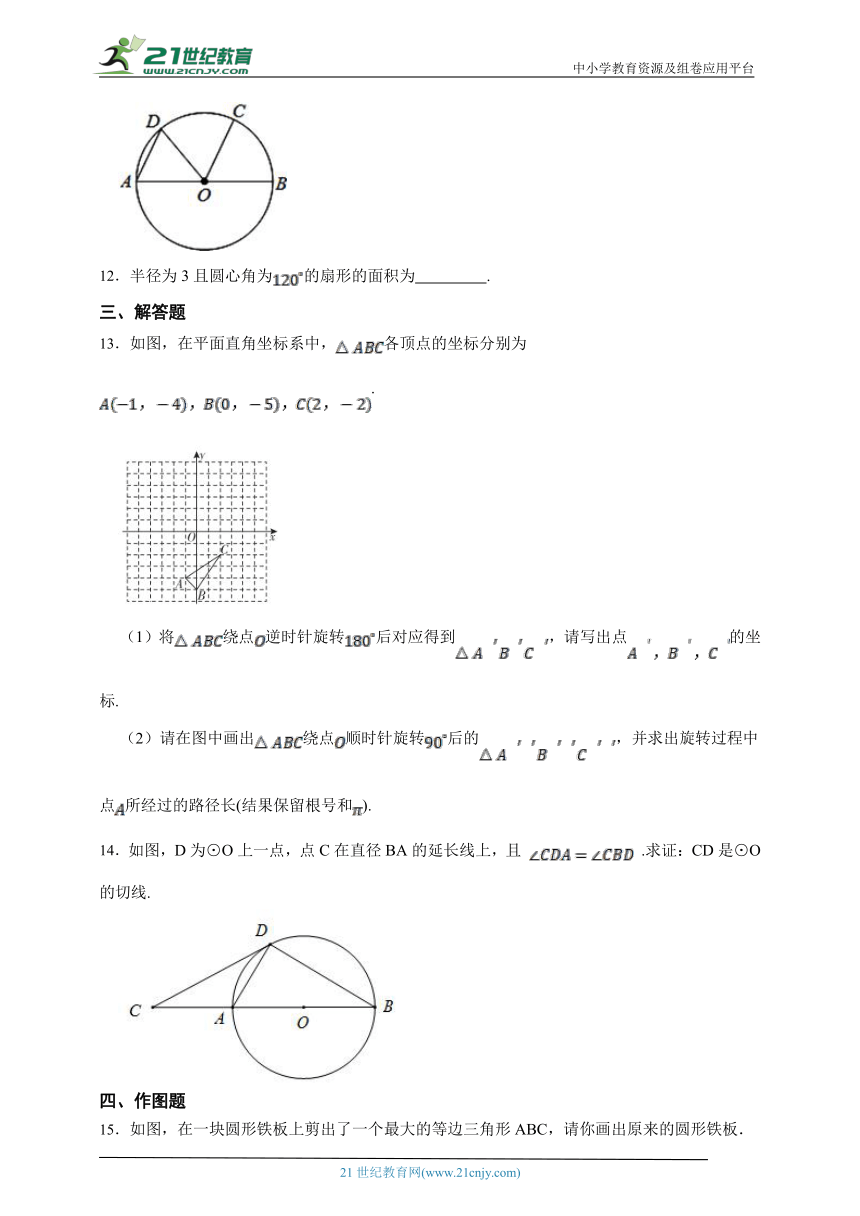
12.半径为3且圆心角为的扇形的面积为 .
三、解答题
13.如图,在平面直角坐标系中,各顶点的坐标分别为.
(1)将绕点逆时针旋转后对应得到,请写出点的坐标.
(2)请在图中画出绕点顺时针旋转后的,并求出旋转过程中点所经过的路径长(结果保留根号和).
14.如图,D为⊙O上一点,点C在直径BA的延长线上,且 .求证:CD是⊙O的切线.
四、作图题
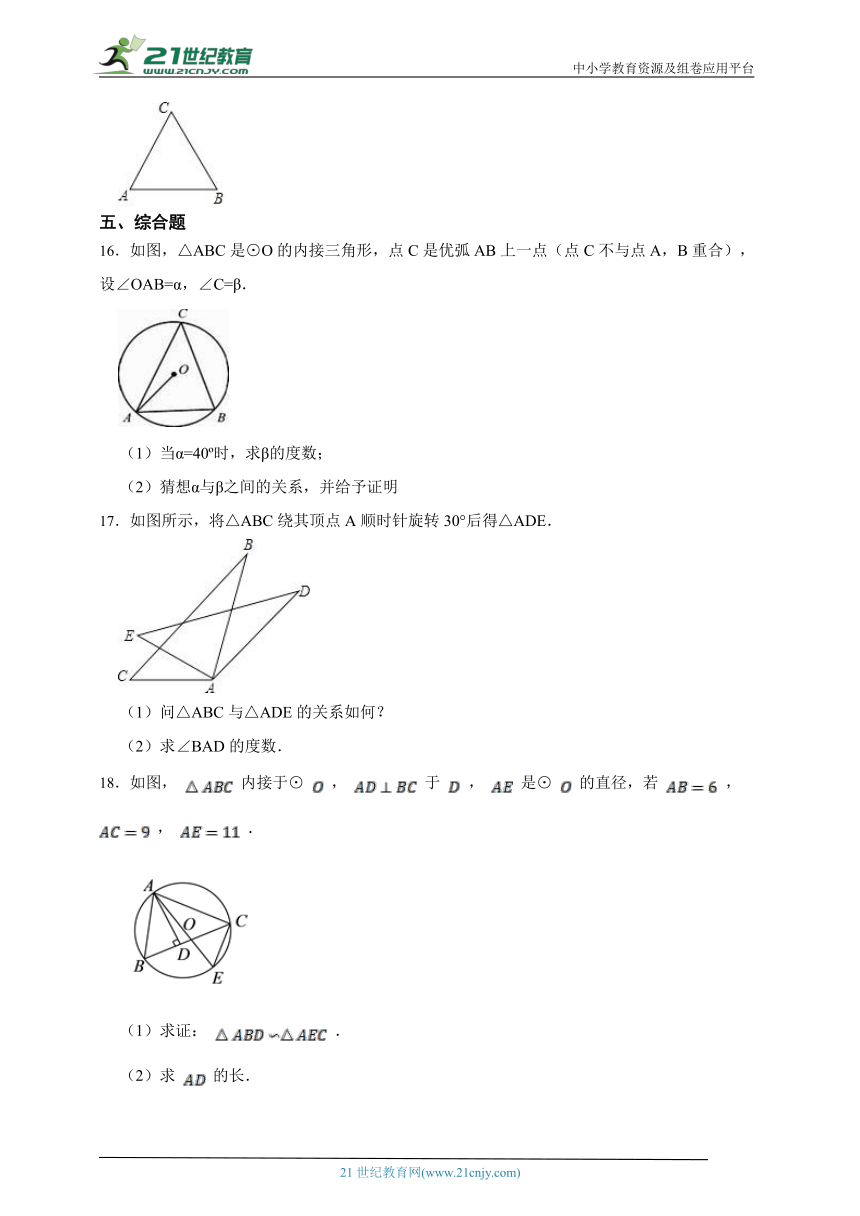
15.如图,在一块圆形铁板上剪出了一个最大的等边三角形ABC,请你画出原来的圆形铁板.
五、综合题
16.如图,△ABC是⊙O的内接三角形,点C是优弧AB上一点(点C不与点A,B重合),设∠OAB=α,∠C=β.
(1)当α=40 时,求β的度数;
(2)猜想α与β之间的关系,并给予证明
17.如图所示,将△ABC绕其顶点A顺时针旋转30°后得△ADE.
(1)问△ABC与△ADE的关系如何?
(2)求∠BAD的度数.
18.如图, 内接于⊙ , 于 , 是⊙ 的直径,若 , , .
(1)求证: .
(2)求 的长.
答案解析部分
1.【答案】B
【知识点】圆周角定理
2.【答案】C
【知识点】弧长的计算
3.【答案】B
【知识点】圆的认识;垂径定理
4.【答案】D
【知识点】圆内接四边形的性质
5.【答案】A
【知识点】点与圆的位置关系
6.【答案】C
【知识点】因式分解法解一元二次方程;三角形的外接圆与外心
7.【答案】4
【知识点】弧长的计算
8.【答案】
【知识点】扇形面积的计算
9.【答案】3≤OP≤5
【知识点】点到直线的距离;勾股定理;垂径定理
10.【答案】60°
【知识点】垂径定理;圆周角定理
11.【答案】65
【知识点】平行线的性质;三角形内角和定理;等腰三角形的性质;圆的认识
12.【答案】3π
【知识点】扇形面积的计算
13.【答案】(1)解:如图,
由题意可得,点,,;
即为所求.
(2)解:由勾股定理得,,
∴旋转过程中点所经过的路径长为.
【知识点】勾股定理;弧长的计算;作图﹣旋转;作图-三角形
14.【答案】证明:连接OD,
∵AB为直径,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
∴CD是⊙O的切线.
【知识点】等腰三角形的性质;圆周角定理;切线的判定
15.【答案】解:如图所示:⊙O即为所求.
【知识点】圆内接正多边形
16.【答案】(1)解:连接OB,
∵OA=OB
∴∠OAB=∠OBA=40°
∴∠AOB=180°-∠OAB-∠OBA=100°
∴∠ACB=∠AOB=50°
即β=50
(2)解:β=90 -α,理由如下:连接OB,∵OA=OB∴∠OAB=∠OBA=α∴∠AOB=180 -2α
∵∠C=
∴β=90 -α
【知识点】等腰三角形的性质;圆周角定理
17.【答案】(1)解:∵△ABC绕其顶点A顺时针旋转30°后得△ADE,∴△ABC≌△ADE
(2)解:旋转角相等,即∠BAD=∠EAC=30°.
【知识点】旋转的性质
18.【答案】(1)证明: 是直径,∴ ,∵ ,
∴ ,
∵ ,
∴
(2)解:∵ ,
,
∴ ,
∴ .
【知识点】圆周角定理;相似三角形的判定与性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
{浙教版九上同步练习}
第三章圆的基本性质(基础知识)检测题
一、单选题
1.如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是弧AC上的点,若∠BOC=40°,则∠D的度数为( )
A.100° B.110° C.120° D.130°
2.某小区内的消防车道有一段弯道,如图,弯道的内外边缘均为圆弧, , 所在圆的圆心为O,点C,D分别在OA,OB上,已知消防车道半径OC=12m,消防车道宽AC=4m, ,则弯道外边缘 的长为( )
A. B. C. D.
3.下列说法中,错误的是( )
A.直径相等的两个圆是等圆
B.平分弦的直径垂直于弦,并且平分弦所对的弧
C.圆中最长的弦是直径
D.一条弦把圆分成两条弧,这两条弧可能是等弧
4.如图,四边形 内接于 ,若 ,则 的大小为( )
A.36° B.54° C.62° D.72°
5.已知的半径为2,若,则点P与的位置关系是( )
A.点P在上 B.点P在内 C.点P在外 D.无法判断
6.已知方程x2-7x+12=0的两根恰好是一个直角三角形的两条直角边的长,则这个直角三角形的外接圆的直径为( )
A.2.5 B.6 C.5 D.
二、填空题
7.在一个圆中60度的圆心角所对的弧长为 ,则该圆的直径为
8.一个扇形的圆心角为135°,弧长为3πcm,则此扇形的面积是 cm2.
9.已知如图,在⊙O中,弦AB的长为8,圆心O到AB的距离为3.若点P是AB上的一动点,则OP的取值范围是 .
10.如图,AC为⊙O的直径,点B在圆上,OD⊥AC交⊙O于点D,连接BD,∠BDO=15°,则∠ACB= .
11.如图,AB为⊙O直径,点C、D在⊙O上,已知∠AOD=50°,AD∥OC,则∠BOC= 度.
12.半径为3且圆心角为的扇形的面积为 .
三、解答题
13.如图,在平面直角坐标系中,各顶点的坐标分别为.
(1)将绕点逆时针旋转后对应得到,请写出点的坐标.
(2)请在图中画出绕点顺时针旋转后的,并求出旋转过程中点所经过的路径长(结果保留根号和).
14.如图,D为⊙O上一点,点C在直径BA的延长线上,且 .求证:CD是⊙O的切线.
四、作图题
15.如图,在一块圆形铁板上剪出了一个最大的等边三角形ABC,请你画出原来的圆形铁板.
五、综合题
16.如图,△ABC是⊙O的内接三角形,点C是优弧AB上一点(点C不与点A,B重合),设∠OAB=α,∠C=β.
(1)当α=40 时,求β的度数;
(2)猜想α与β之间的关系,并给予证明
17.如图所示,将△ABC绕其顶点A顺时针旋转30°后得△ADE.
(1)问△ABC与△ADE的关系如何?
(2)求∠BAD的度数.
18.如图, 内接于⊙ , 于 , 是⊙ 的直径,若 , , .
(1)求证: .
(2)求 的长.
答案解析部分
1.【答案】B
【知识点】圆周角定理
2.【答案】C
【知识点】弧长的计算
3.【答案】B
【知识点】圆的认识;垂径定理
4.【答案】D
【知识点】圆内接四边形的性质
5.【答案】A
【知识点】点与圆的位置关系
6.【答案】C
【知识点】因式分解法解一元二次方程;三角形的外接圆与外心
7.【答案】4
【知识点】弧长的计算
8.【答案】
【知识点】扇形面积的计算
9.【答案】3≤OP≤5
【知识点】点到直线的距离;勾股定理;垂径定理
10.【答案】60°
【知识点】垂径定理;圆周角定理
11.【答案】65
【知识点】平行线的性质;三角形内角和定理;等腰三角形的性质;圆的认识
12.【答案】3π
【知识点】扇形面积的计算
13.【答案】(1)解:如图,
由题意可得,点,,;
即为所求.
(2)解:由勾股定理得,,
∴旋转过程中点所经过的路径长为.
【知识点】勾股定理;弧长的计算;作图﹣旋转;作图-三角形
14.【答案】证明:连接OD,
∵AB为直径,
∴ ,
又∵ ,
∴ ,
∴ ,
∴ ,
∴CD是⊙O的切线.
【知识点】等腰三角形的性质;圆周角定理;切线的判定
15.【答案】解:如图所示:⊙O即为所求.
【知识点】圆内接正多边形
16.【答案】(1)解:连接OB,
∵OA=OB
∴∠OAB=∠OBA=40°
∴∠AOB=180°-∠OAB-∠OBA=100°
∴∠ACB=∠AOB=50°
即β=50
(2)解:β=90 -α,理由如下:连接OB,∵OA=OB∴∠OAB=∠OBA=α∴∠AOB=180 -2α
∵∠C=
∴β=90 -α
【知识点】等腰三角形的性质;圆周角定理
17.【答案】(1)解:∵△ABC绕其顶点A顺时针旋转30°后得△ADE,∴△ABC≌△ADE
(2)解:旋转角相等,即∠BAD=∠EAC=30°.
【知识点】旋转的性质
18.【答案】(1)证明: 是直径,∴ ,∵ ,
∴ ,
∵ ,
∴
(2)解:∵ ,
,
∴ ,
∴ .
【知识点】圆周角定理;相似三角形的判定与性质
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
