{浙教版九上同步练习} 第三章 圆的基本性质(培优)检测题(含答案)
文档属性
| 名称 | {浙教版九上同步练习} 第三章 圆的基本性质(培优)检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-31 17:59:29 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
{浙教版九上同步练习}
第三章圆的基本性质(培优)检测题
一、单选题
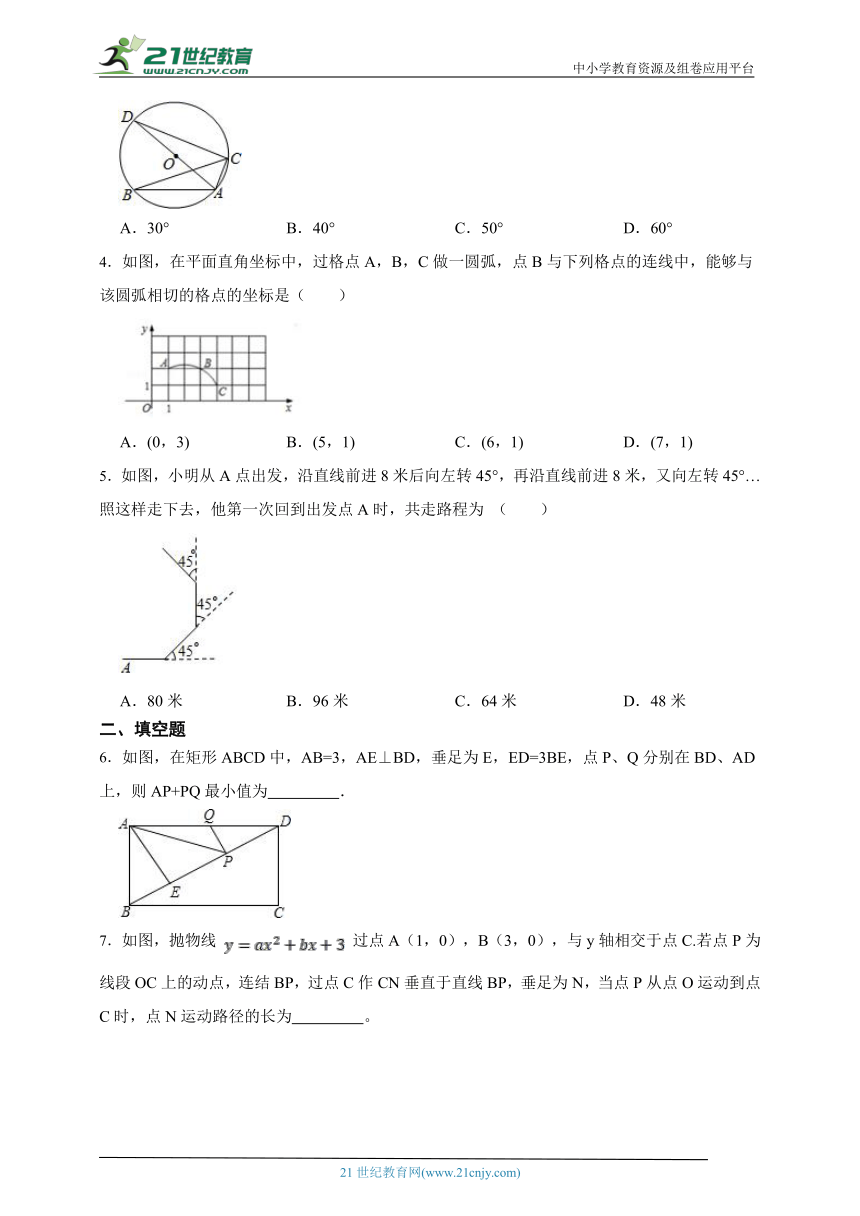
1.如图,在矩形ABCD中,,,E是BC的中点,将沿直线AE翻折,点B落在点F处,连接CF,则CF的长为( )
A. B. C. D.
2.已知锐角∠AOB如图,
⑴在射线OA上取一点C,以点O为圆心,OC长为半径作 ,交射线OB于点D,连接CD;
⑵分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;
⑶连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )
A.∠COM=∠COD B.若OM=MN,则∠AOB=20°
C.MN∥CD D.MN=3CD
3.如图,⊙O外接于△ABC,AD为⊙O的直径,∠ABC=30°,则∠CAD=( )
A.30° B.40° C.50° D.60°
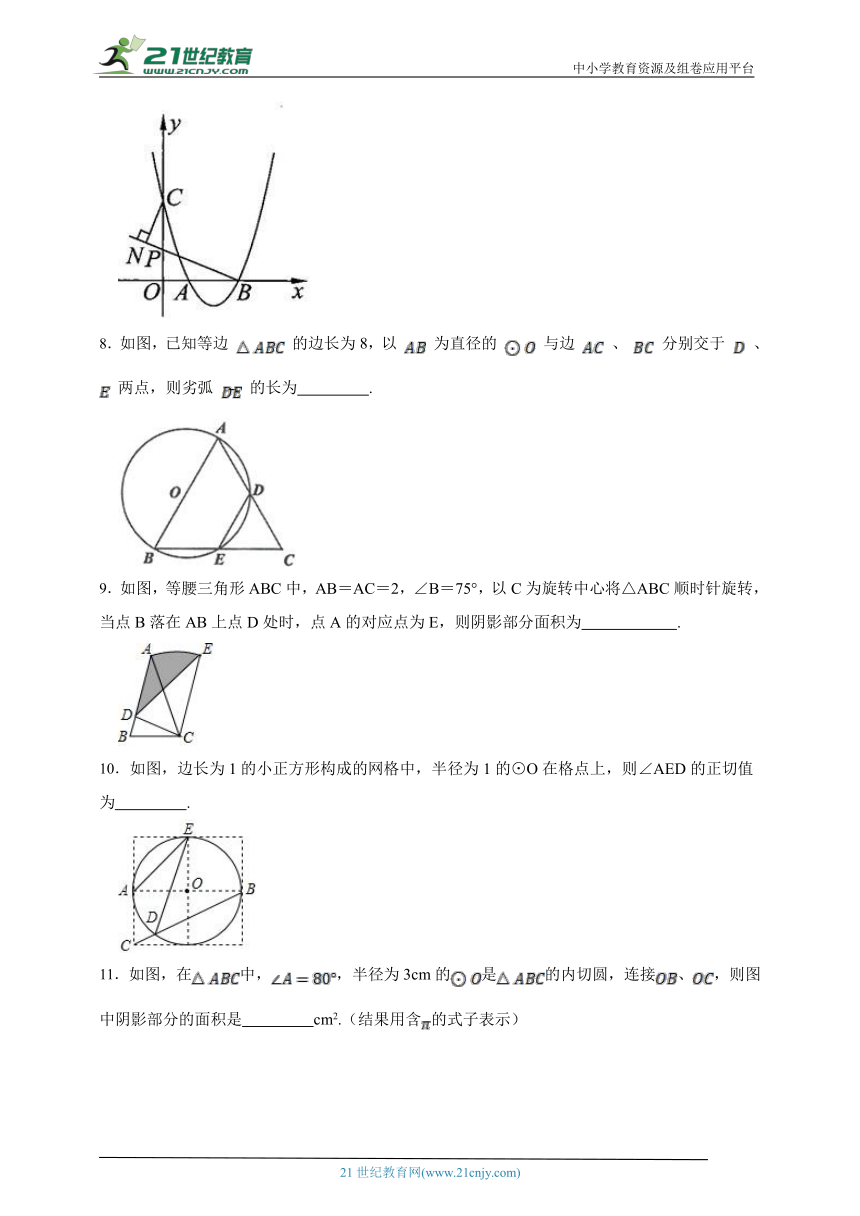
4.如图,在平面直角坐标中,过格点A,B,C做一圆弧,点B与下列格点的连线中,能够与该圆弧相切的格点的坐标是( )
A.(0,3) B.(5,1) C.(6,1) D.(7,1)
5.如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为 ( )
A.80米 B.96米 C.64米 D.48米
二、填空题
6.如图,在矩形ABCD中,AB=3,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD、AD上,则AP+PQ最小值为 .
7.如图,抛物线 过点A(1,0),B(3,0),与y轴相交于点C.若点P为线段OC上的动点,连结BP,过点C作CN垂直于直线BP,垂足为N,当点P从点O运动到点C时,点N运动路径的长为 。
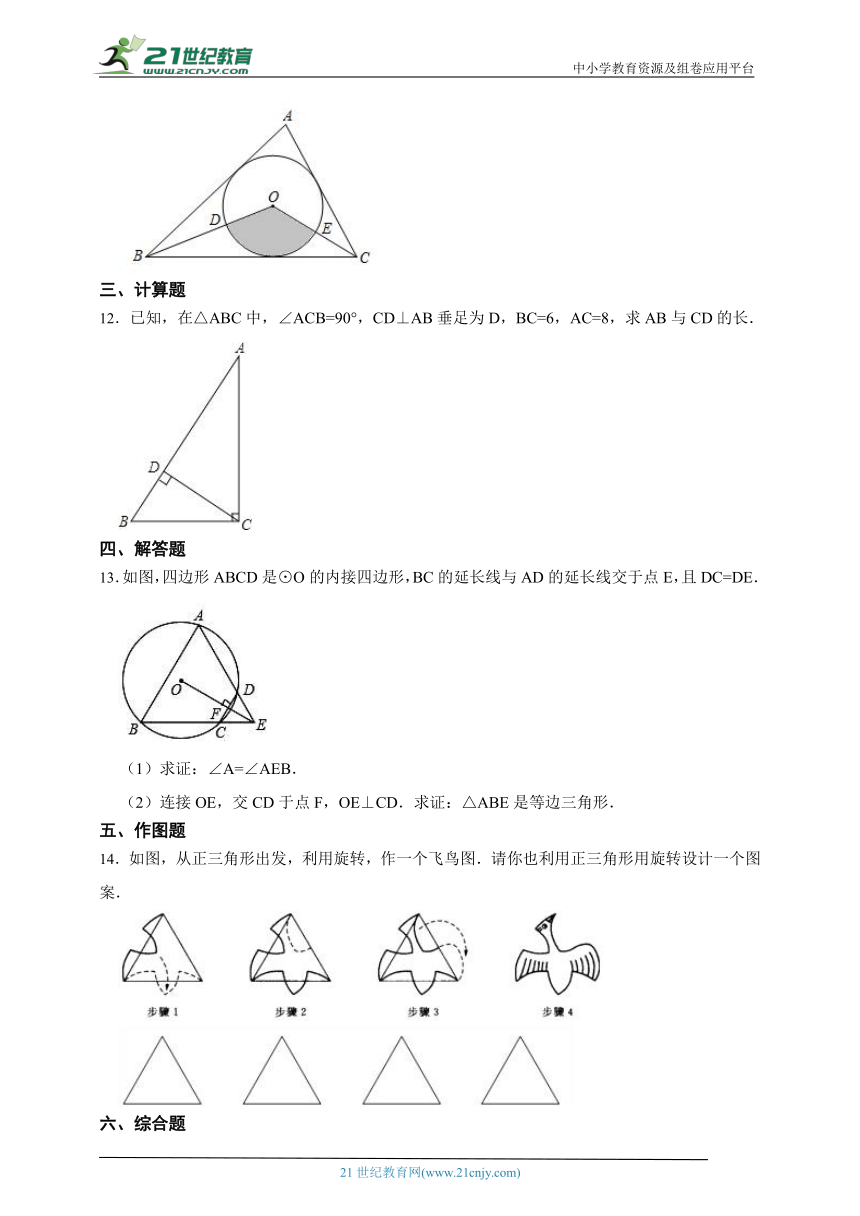
8.如图,已知等边 的边长为8,以 为直径的 与边 、 分别交于 、 两点,则劣弧 的长为 .
9.如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为 .
10.如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为 .
11.如图,在中,,半径为3cm的是的内切圆,连接、,则图中阴影部分的面积是 cm2.(结果用含的式子表示)
三、计算题
12.已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.
四、解答题
13.如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
(1)求证:∠A=∠AEB.
(2)连接OE,交CD于点F,OE⊥CD.求证:△ABE是等边三角形.
五、作图题
14.如图,从正三角形出发,利用旋转,作一个飞鸟图.请你也利用正三角形用旋转设计一个图案.
六、综合题
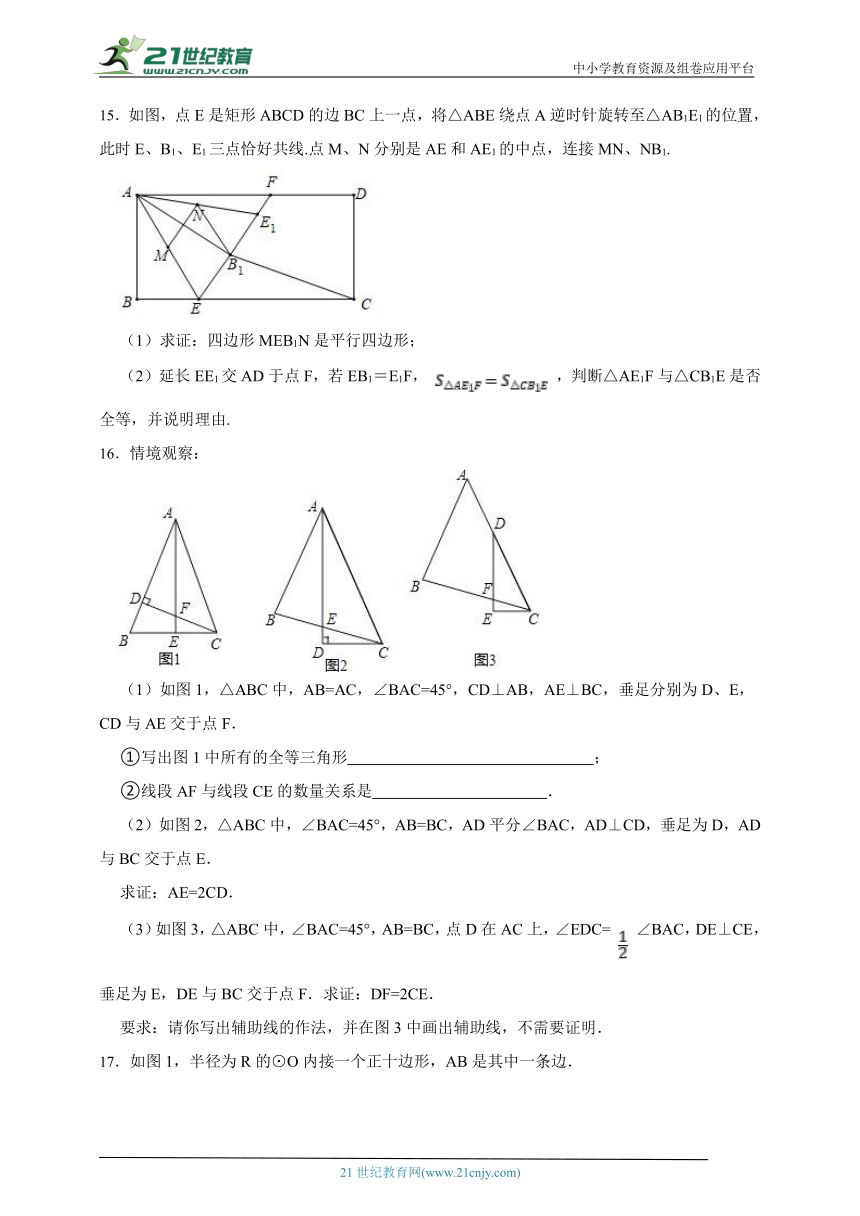
15.如图,点E是矩形ABCD的边BC上一点,将△ABE绕点A逆时针旋转至△AB1E1的位置,此时E、B1、E1三点恰好共线.点M、N分别是AE和AE1的中点,连接MN、NB1.
(1)求证:四边形MEB1N是平行四边形;
(2)延长EE1交AD于点F,若EB1=E1F, ,判断△AE1F与△CB1E是否全等,并说明理由.
16.情境观察:
(1)如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 .
(2)如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
(3)如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC= ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
17.如图1,半径为R的⊙O内接一个正十边形,AB是其中一条边.
(1)用R和含18°的三角函数的式子表示边长AB.
(2)如图2,作∠ABO的平分线与半径OA交于点C,试猜想(1)中)18°的三角函数和黄金比有怎样的关系,并说明理由.
七、实践探究题
18.定义:如图1,点、把线段分割成、和,若以、、为边的三角形是一个直角三角形,则称点、是线段的勾股分割点.
(1)已知点、是线段的勾股分割点,,,若,,则 .
(2)如图,在等腰直角中,,、为直线上两点,满足.
①如图2,点、在线段上,求证:点、是线段的勾股分割点;
②如图3,若点在线段上,点在线段的延长线上,,,求的长.
答案解析部分
1.【答案】D
【知识点】勾股定理;矩形的性质;旋转的性质;直角三角形斜边上的中线
2.【答案】D
【知识点】平行线的判定;等边三角形的判定与性质;圆周角定理
3.【答案】D
【知识点】三角形内角和定理;圆周角定理
4.【答案】B
【知识点】坐标与图形性质;垂径定理
5.【答案】C
【知识点】多边形内角与外角;正多边形的性质
6.【答案】
【知识点】勾股定理;矩形的性质;轴对称的应用-最短距离问题;相似三角形的判定与性质
7.【答案】
【知识点】勾股定理;弧长的计算
8.【答案】
【知识点】等边三角形的判定与性质;弧长的计算
9.【答案】
【知识点】扇形面积的计算;旋转的性质
10.【答案】
【知识点】圆周角定理;切线的性质;锐角三角函数的定义
11.【答案】
【知识点】三角形的内切圆与内心;扇形面积的计算
12.【答案】解:在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,由勾股定理得:AB= =10,∵S△ABC= AB CD= AC BC,∴CD= = =4.8
【知识点】勾股定理
13.【答案】(1)解:∵四边形ABCD是⊙O的内接四边形,∴∠A+∠BCD=180°,∵∠DCE+∠BCD=180°,∴∠A=∠DCE,∵DC=DE,∴∠DCE=∠AEB,∴∠A=∠AEB
(2)解:∵∠A=∠AEB,∴△ABE是等腰三角形,∵EO⊥CD,∴CF=DF,∴EO是CD的垂直平分线,∴ED=EC,∵DC=DE,∴DC=DE=EC,∴△DCE是等边三角形,∴∠AEB=60°,∴△ABE是等边三角形.
【知识点】圆内接四边形的性质
14.【答案】解:先以等边三角形的一边为基础画一个基本图形,再绕等边三角形的两个顶点分别旋转60°后删除原等边三角形.
如图所示:
【知识点】利用旋转设计图案
15.【答案】(1)证明:∵四边形ABCD是矩形,
∴∠B=90°,
∵△AB1E1是△ABE旋转所得的,
∴AE=AE1,∠AB1E1=∠AB1E=∠B=90°,
∴B1是EE1的中点,
∴EB1= EE1,
∵M、N分别是AE和AE1的中点,
∴MN∥EB1,MN= EE1,
∴EB1=MN,
∴四边形MEB1N为平行四边形,
(2)解:△AE1F≌△CEB1,
证明:连接FC,
∵EB1=B1E1=E1F,
∴S△AE1F=S△AEB1=S△AE1B1= S△EAF,
同理,S△EB1C= SFEC,
∵S△AE1F=S△EB1C,
∴S△EAF=S△FEC,
∵AF∥EC,
∴△AEF底边AF上的高和△FEC底边上的高相等.
∴AF=EC.
∵AF∥EC,
∴∠AFE=∠FEC,
在△AE1F和△CEB1中,
,
∴△AE1F≌△CEB1(SAS).
【知识点】三角形的面积;平行四边形的判定;旋转的性质;三角形全等的判定(SAS);三角形的中位线定理
16.【答案】(1)△ABE≌△ACE,△ADF≌△CDB;AF=2CE 问题探究:
(2)证明:延长AB、CD交于点G,如图2‘所示:
∵AD平分∠BAC,
∴∠CAD=∠GAD,
∵AD⊥CD,
∴∠ADC=∠ADG=90°,
在△ADC和△ADG中,
,
∴△ADC≌△ADG(ASA),
∴CD=GD,即CG=2CD,
∵∠BAC=45°,AB=BC,
∴∠ABC=90°,
∴∠CBG=90°,
∴∠G+∠BCG=90°,
∵∠G+∠BAE=90°,
∴∠BAE=∠BCG,
在△ABE和△CBG中,
,
∴△ADC≌△CBG中(ASA),
∴AE=CG=2CD
拓展延伸:
(3)解:作DG⊥BC交CE的延长线于G,
如图3所示.
【知识点】全等三角形的判定与性质
17.【答案】(1)解:作OD⊥AB,如图.
由题意,得 ,
∵OA=OB,OD⊥AB,
∴∠AOD=18°,AD=AB,
;
(2)解: 平分 ,
.
,
由(1)得,AB=2Rsin18",
解得 : (舍负),
即 .
【知识点】等腰三角形的判定与性质;圆内接正多边形;相似三角形的判定与性质;解直角三角形—边角关系
18.【答案】(1)
(2)解:①证明:∵,,
∴,
将绕点C逆时针旋转得到,连接,,
∴,,,
∴,
∵,,
∴,
∵,,
∴,
∴,
∵,
∴,
∴点、是线段的勾股分割点;
②将绕点C逆时针旋转得到,连接,
∴,,,,
∴,
∵,
∴,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∴.
【知识点】勾股定理的应用;旋转的性质;直角三角形的性质;三角形全等的判定(SAS)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
{浙教版九上同步练习}
第三章圆的基本性质(培优)检测题
一、单选题
1.如图,在矩形ABCD中,,,E是BC的中点,将沿直线AE翻折,点B落在点F处,连接CF,则CF的长为( )
A. B. C. D.
2.已知锐角∠AOB如图,
⑴在射线OA上取一点C,以点O为圆心,OC长为半径作 ,交射线OB于点D,连接CD;
⑵分别以点C,D为圆心,CD长为半径作弧,交 于点M,N;
⑶连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )
A.∠COM=∠COD B.若OM=MN,则∠AOB=20°
C.MN∥CD D.MN=3CD
3.如图,⊙O外接于△ABC,AD为⊙O的直径,∠ABC=30°,则∠CAD=( )
A.30° B.40° C.50° D.60°
4.如图,在平面直角坐标中,过格点A,B,C做一圆弧,点B与下列格点的连线中,能够与该圆弧相切的格点的坐标是( )
A.(0,3) B.(5,1) C.(6,1) D.(7,1)
5.如图,小明从A点出发,沿直线前进8米后向左转45°,再沿直线前进8米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为 ( )
A.80米 B.96米 C.64米 D.48米
二、填空题
6.如图,在矩形ABCD中,AB=3,AE⊥BD,垂足为E,ED=3BE,点P、Q分别在BD、AD上,则AP+PQ最小值为 .
7.如图,抛物线 过点A(1,0),B(3,0),与y轴相交于点C.若点P为线段OC上的动点,连结BP,过点C作CN垂直于直线BP,垂足为N,当点P从点O运动到点C时,点N运动路径的长为 。
8.如图,已知等边 的边长为8,以 为直径的 与边 、 分别交于 、 两点,则劣弧 的长为 .
9.如图,等腰三角形ABC中,AB=AC=2,∠B=75°,以C为旋转中心将△ABC顺时针旋转,当点B落在AB上点D处时,点A的对应点为E,则阴影部分面积为 .
10.如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为 .
11.如图,在中,,半径为3cm的是的内切圆,连接、,则图中阴影部分的面积是 cm2.(结果用含的式子表示)
三、计算题
12.已知,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,求AB与CD的长.
四、解答题
13.如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
(1)求证:∠A=∠AEB.
(2)连接OE,交CD于点F,OE⊥CD.求证:△ABE是等边三角形.
五、作图题
14.如图,从正三角形出发,利用旋转,作一个飞鸟图.请你也利用正三角形用旋转设计一个图案.
六、综合题
15.如图,点E是矩形ABCD的边BC上一点,将△ABE绕点A逆时针旋转至△AB1E1的位置,此时E、B1、E1三点恰好共线.点M、N分别是AE和AE1的中点,连接MN、NB1.
(1)求证:四边形MEB1N是平行四边形;
(2)延长EE1交AD于点F,若EB1=E1F, ,判断△AE1F与△CB1E是否全等,并说明理由.
16.情境观察:
(1)如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 .
(2)如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
(3)如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC= ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
17.如图1,半径为R的⊙O内接一个正十边形,AB是其中一条边.
(1)用R和含18°的三角函数的式子表示边长AB.
(2)如图2,作∠ABO的平分线与半径OA交于点C,试猜想(1)中)18°的三角函数和黄金比有怎样的关系,并说明理由.
七、实践探究题
18.定义:如图1,点、把线段分割成、和,若以、、为边的三角形是一个直角三角形,则称点、是线段的勾股分割点.
(1)已知点、是线段的勾股分割点,,,若,,则 .
(2)如图,在等腰直角中,,、为直线上两点,满足.
①如图2,点、在线段上,求证:点、是线段的勾股分割点;
②如图3,若点在线段上,点在线段的延长线上,,,求的长.
答案解析部分
1.【答案】D
【知识点】勾股定理;矩形的性质;旋转的性质;直角三角形斜边上的中线
2.【答案】D
【知识点】平行线的判定;等边三角形的判定与性质;圆周角定理
3.【答案】D
【知识点】三角形内角和定理;圆周角定理
4.【答案】B
【知识点】坐标与图形性质;垂径定理
5.【答案】C
【知识点】多边形内角与外角;正多边形的性质
6.【答案】
【知识点】勾股定理;矩形的性质;轴对称的应用-最短距离问题;相似三角形的判定与性质
7.【答案】
【知识点】勾股定理;弧长的计算
8.【答案】
【知识点】等边三角形的判定与性质;弧长的计算
9.【答案】
【知识点】扇形面积的计算;旋转的性质
10.【答案】
【知识点】圆周角定理;切线的性质;锐角三角函数的定义
11.【答案】
【知识点】三角形的内切圆与内心;扇形面积的计算
12.【答案】解:在△ABC中,∠ACB=90°,CD⊥AB垂足为D,BC=6,AC=8,由勾股定理得:AB= =10,∵S△ABC= AB CD= AC BC,∴CD= = =4.8
【知识点】勾股定理
13.【答案】(1)解:∵四边形ABCD是⊙O的内接四边形,∴∠A+∠BCD=180°,∵∠DCE+∠BCD=180°,∴∠A=∠DCE,∵DC=DE,∴∠DCE=∠AEB,∴∠A=∠AEB
(2)解:∵∠A=∠AEB,∴△ABE是等腰三角形,∵EO⊥CD,∴CF=DF,∴EO是CD的垂直平分线,∴ED=EC,∵DC=DE,∴DC=DE=EC,∴△DCE是等边三角形,∴∠AEB=60°,∴△ABE是等边三角形.
【知识点】圆内接四边形的性质
14.【答案】解:先以等边三角形的一边为基础画一个基本图形,再绕等边三角形的两个顶点分别旋转60°后删除原等边三角形.
如图所示:
【知识点】利用旋转设计图案
15.【答案】(1)证明:∵四边形ABCD是矩形,
∴∠B=90°,
∵△AB1E1是△ABE旋转所得的,
∴AE=AE1,∠AB1E1=∠AB1E=∠B=90°,
∴B1是EE1的中点,
∴EB1= EE1,
∵M、N分别是AE和AE1的中点,
∴MN∥EB1,MN= EE1,
∴EB1=MN,
∴四边形MEB1N为平行四边形,
(2)解:△AE1F≌△CEB1,
证明:连接FC,
∵EB1=B1E1=E1F,
∴S△AE1F=S△AEB1=S△AE1B1= S△EAF,
同理,S△EB1C= SFEC,
∵S△AE1F=S△EB1C,
∴S△EAF=S△FEC,
∵AF∥EC,
∴△AEF底边AF上的高和△FEC底边上的高相等.
∴AF=EC.
∵AF∥EC,
∴∠AFE=∠FEC,
在△AE1F和△CEB1中,
,
∴△AE1F≌△CEB1(SAS).
【知识点】三角形的面积;平行四边形的判定;旋转的性质;三角形全等的判定(SAS);三角形的中位线定理
16.【答案】(1)△ABE≌△ACE,△ADF≌△CDB;AF=2CE 问题探究:
(2)证明:延长AB、CD交于点G,如图2‘所示:
∵AD平分∠BAC,
∴∠CAD=∠GAD,
∵AD⊥CD,
∴∠ADC=∠ADG=90°,
在△ADC和△ADG中,
,
∴△ADC≌△ADG(ASA),
∴CD=GD,即CG=2CD,
∵∠BAC=45°,AB=BC,
∴∠ABC=90°,
∴∠CBG=90°,
∴∠G+∠BCG=90°,
∵∠G+∠BAE=90°,
∴∠BAE=∠BCG,
在△ABE和△CBG中,
,
∴△ADC≌△CBG中(ASA),
∴AE=CG=2CD
拓展延伸:
(3)解:作DG⊥BC交CE的延长线于G,
如图3所示.
【知识点】全等三角形的判定与性质
17.【答案】(1)解:作OD⊥AB,如图.
由题意,得 ,
∵OA=OB,OD⊥AB,
∴∠AOD=18°,AD=AB,
;
(2)解: 平分 ,
.
,
由(1)得,AB=2Rsin18",
解得 : (舍负),
即 .
【知识点】等腰三角形的判定与性质;圆内接正多边形;相似三角形的判定与性质;解直角三角形—边角关系
18.【答案】(1)
(2)解:①证明:∵,,
∴,
将绕点C逆时针旋转得到,连接,,
∴,,,
∴,
∵,,
∴,
∵,,
∴,
∴,
∵,
∴,
∴点、是线段的勾股分割点;
②将绕点C逆时针旋转得到,连接,
∴,,,,
∴,
∵,
∴,
∴,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∴,
∴.
【知识点】勾股定理的应用;旋转的性质;直角三角形的性质;三角形全等的判定(SAS)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
