【浙教版九上同步练习】九年级上册综合练习数学试题一(含答案)
文档属性
| 名称 | 【浙教版九上同步练习】九年级上册综合练习数学试题一(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-01 17:01:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【浙教版九上同步练习】
九上全册综合题一
一、单选题
1.下列说法正确的是( )
A.对角线相等的四边形是矩形
B.有两边及一角对应相等的两个三角形全等
C.对角线互相垂直的矩形是正方形
D.平分弦的直径垂直于弦
2.赵希的笔袋里装有5支同一品牌、同一型号的中性笔,其中有2支黑色,2支红色和1支蓝色,上课时,赵希随机的从笔袋中取出一只,若正好是黑色中性笔的概率是( )
A. B. C. D.
3.抛物线的 顶点坐标是( )
A. B. C. D.
4.如图,是二次函数的图象,则下列四个结论中正确的有( )
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
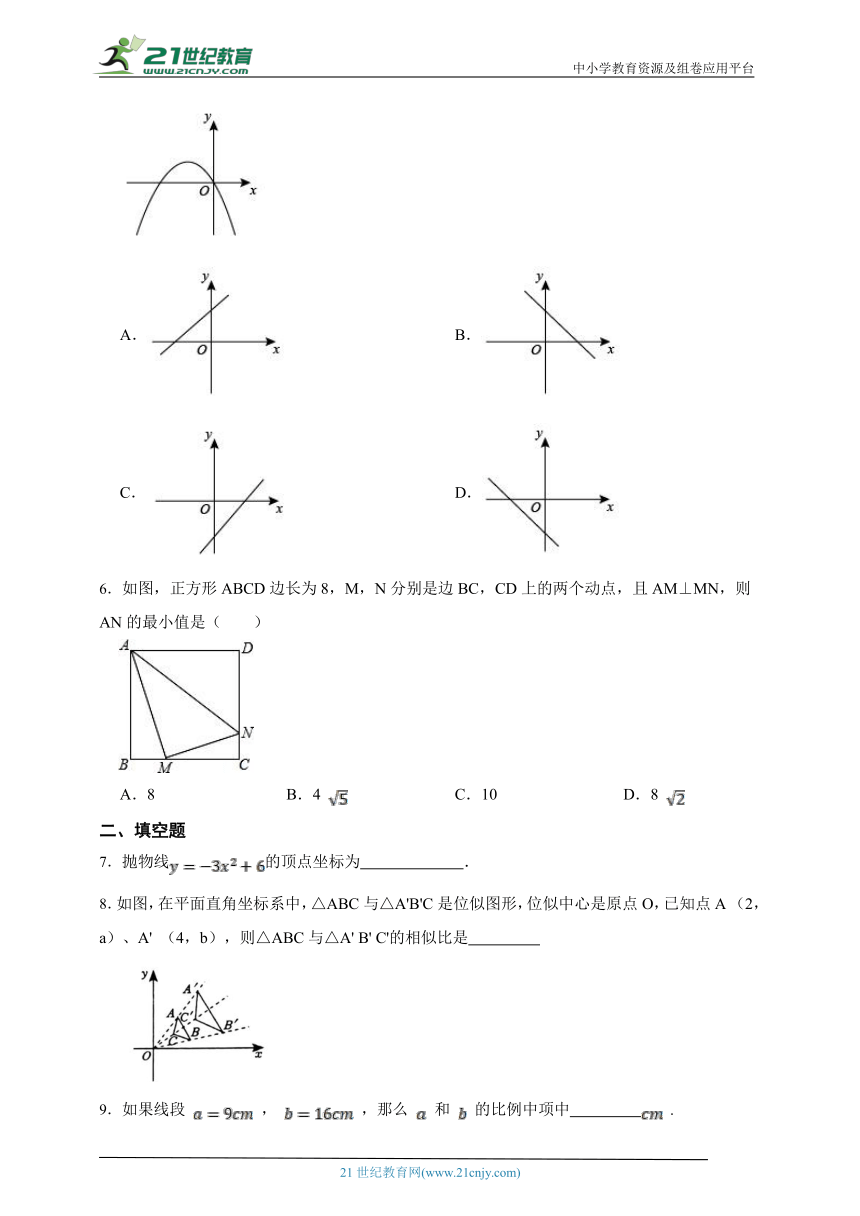
5.二次函数的图象如图所示,则一次函数的图象大致是( )
A. B.
C. D.
6.如图,正方形ABCD边长为8,M,N分别是边BC,CD上的两个动点,且AM⊥MN,则AN的最小值是( )
A.8 B.4 C.10 D.8
二、填空题
7.抛物线的顶点坐标为 .
8.如图,在平面直角坐标系中,△ABC与△A'B'C是位似图形,位似中心是原点O,已知点A (2,a)、A' (4,b),则△ABC与△A' B' C'的相似比是
9.如果线段 , ,那么 和 的比例中项中 .
10.如图,扇形圆心角为直角,,点在上,以,为邻边构造菱形,边交于点,若,则图中两块阴影部分的面积和为 结果保留到
三、判断题
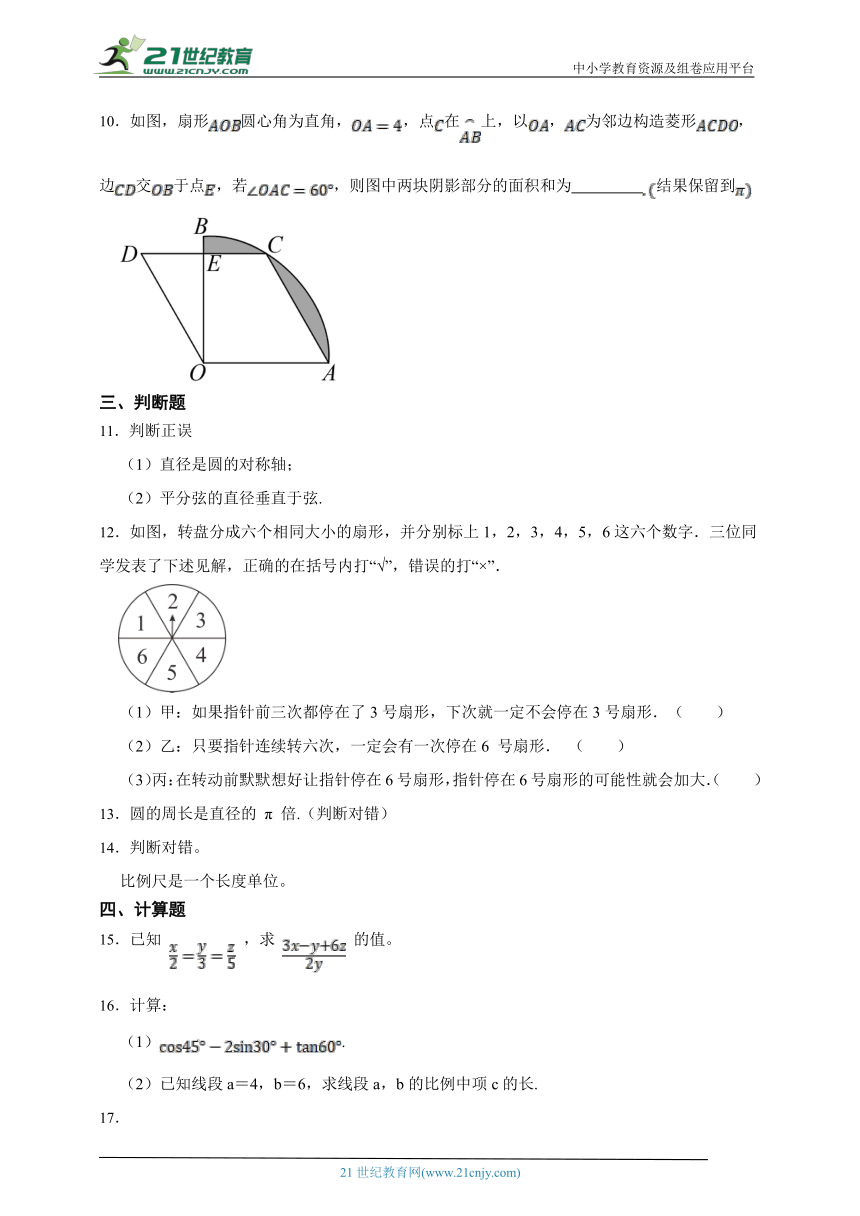
11.判断正误
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
12.如图,转盘分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字.三位同学发表了下述见解,正确的在括号内打“√”,错误的打“×”.
(1)甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形.( )
(2)乙:只要指针连续转六次,一定会有一次停在6 号扇形. ( )
(3)丙:在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大.( )
13.圆的周长是直径的 π 倍.(判断对错)
14.判断对错。
比例尺是一个长度单位。
四、计算题
15.已知 ,求 的值。
16.计算:
(1).
(2)已知线段a=4,b=6,求线段a,b的比例中项c的长.
17.
(1)解方程:2x2+1=3x;
(2)将二次函数 配方成y=a(x﹣h)2+k的形式.
五、解答题
18.一个不透明的盒子中装有两个红球,一个白球和一个黄球,这些球除颜色外都相同,从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,请你用列表法或画树状图法求两次摸到的球的颜色都是红色的概率.
19.如图,在 中,点 , , 分别在 , , 上, , .若 , , ,求 的长.
20.小宇和小伟玩“石头、剪刀、布”的游戏.这个游戏的规则是:“剪刀”胜“布”,“布”胜“石头”,“石头”胜“剪刀”,手势相同不分胜负.如果二人同时随机出手(分别出三种手势中的一种手势)一次,那么小宇获胜的概率是多少?
六、作图题
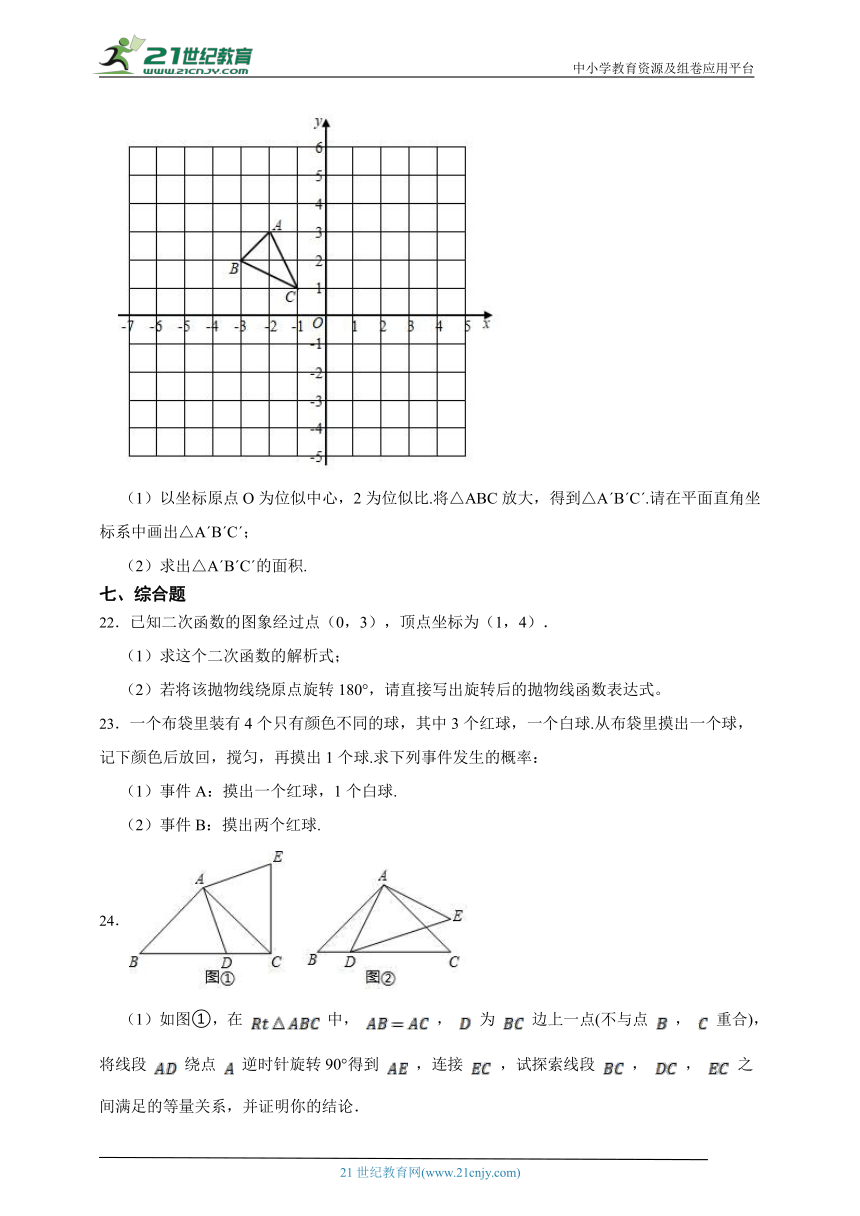
21.如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(﹣2,3),B(﹣3,2),C(﹣1,1).
(1)以坐标原点O为位似中心,2为位似比.将△ABC放大,得到△A B C .请在平面直角坐标系中画出△A B C ;
(2)求出△A B C 的面积.
七、综合题
22.已知二次函数的图象经过点(0,3),顶点坐标为(1,4).
(1)求这个二次函数的解析式;
(2)若将该抛物线绕原点旋转180°,请直接写出旋转后的抛物线函数表达式。
23.一个布袋里装有4个只有颜色不同的球,其中3个红球,一个白球.从布袋里摸出一个球,记下颜色后放回,搅匀,再摸出1个球.求下列事件发生的概率:
(1)事件A:摸出一个红球,1个白球.
(2)事件B:摸出两个红球.
24.
(1)如图①,在 中, , 为 边上一点(不与点 , 重合),将线段 绕点 逆时针旋转90°得到 ,连接 ,试探索线段 , , 之间满足的等量关系,并证明你的结论.
(2)如图②,在 与 中, , ,将 绕点 旋转,使点 落在 边上,试探索线段 , , 之间满足的等量关系,并证明你的结论.
25.问题背景:如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC、BC、CD之间的数量关系.
小吴同学探究此问题的思路是:将ΔBCD绕点D逆时针旋转90°到ΔAED处,点B、C分别落在点A、E处(如图②),易证点C、A、E在同一条直线上,并且ΔCDE是等腰直角三角形,所以CE= CD,从而得出结论:AC+BC= CD.
图①
图②
图③
图④
简单应用:
(1)在图①中,若AC= ,BC=2 ,则CD= .
(2)如图③,AB是⊙O的直径,点C、D在⊙O上,弧AD=弧BD,若AB=13,BC=12,求CD的长.
(3)拓展延伸:
如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m答案解析部分
1.【答案】C
【知识点】三角形全等的判定;矩形的判定;正方形的性质;垂径定理
2.【答案】D
【知识点】概率公式
3.【答案】A
【知识点】二次函数y=a(x-h)^2+k的图象
4.【答案】C
【知识点】二次函数图象与系数的关系;二次函数y=ax^2+bx+c的性质
5.【答案】B
【知识点】二次函数图象与系数的关系;一次函数图象、性质与系数的关系
6.【答案】C
【知识点】二次函数的最值;相似三角形的判定与性质
7.【答案】(0,6)
【知识点】二次函数y=a(x-h)^2+k的图象
8.【答案】1:2
【知识点】位似变换
9.【答案】12
【知识点】比例的性质
10.【答案】
【知识点】菱形的性质;扇形面积的计算
11.【答案】(1)正确
(2)错误
【知识点】垂径定理
12.【答案】(1)错误
(2)错误
(3)错误
【知识点】事件发生的可能性
13.【答案】正确
【知识点】圆的认识
14.【答案】错误
【知识点】比例尺
15.【答案】解:∵ ,∴可设x=2k,则y=3k,z=5k
∴
【知识点】比例的性质
16.【答案】(1)解:原式
(2)解:解:由题意得,,a=4,b=6,,
∴.
【知识点】比例的性质;特殊角的三角函数值
17.【答案】(1)解:∵2x2﹣3x+1=0,
∴(2x﹣1)(x﹣1)=0,
解得:x1= ,x2=1;
(2)解: ,
,
= .
【知识点】因式分解法解一元二次方程;二次函数y=ax^2+bx+c与二次函数y=a(x-h)^2+k的转化
18.【答案】解:画树状图为:
共有12种等可能的结果数,两次摸到的球的颜色都是红色的结果数为2,
∴摸到的两个球的颜色都是红色的概率= .
【知识点】列表法与树状图法
19.【答案】解:∵ ,
∴
∵ , ,
∴
解得
【知识点】平行线分线段成比例
20.【答案】解:画树状图如下,
所有机会均等的情况共9种,小宇获胜的概率为:,
答:小宇获胜的概率是.
【知识点】列表法与树状图法;概率公式
21.【答案】(1)解:如图,△A'B'C'即为所求;
(2)解:△A'B'C的面积=4S△ABC=4(2×2﹣ ×1×1﹣ ×1×2﹣ ×1×2)=6.
【知识点】作图﹣位似变换
22.【答案】(1)解:设二次函数解析式为y=a(x﹣1)2+4,把点(0,3)代入得a+4=3,
解得:a=﹣1,∴这个二次函数解析式为y=﹣(x﹣1)2+4.
(2)解:y=(x+1)2-4
【知识点】二次函数图象的几何变换;待定系数法求二次函数解析式
23.【答案】(1)解:画树状图得:
∵共有16种等可能的结果,摸出一个红球,1个白球的有6种情况,
∴P(事件A)= = ;
(2)解:∵摸出两个红球的有9种情况,
∴P(事件B)= .
【知识点】列表法与树状图法;概率公式
24.【答案】(1)解: BC=DC+EC,证明如下:
∵将线段AD绕点A逆时针旋转90°得到AE,
∴AD=AE,∠DAE=90°,
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,
∴BC=DC+BD=DC+EC;
(2)BD2+CD2=2AD2,证明如下:
连接CE,
由(1)得,△BAD≌△CAE,
∴BD=CE,∠ACE=∠B,
∴∠DCE=90°,
∴CE2+CD2=ED2,
在Rt△ADE中,AD2+AE2=ED2,又AD=AE,
∴BD2+CD2=2AD2.
【知识点】旋转的性质;三角形全等的判定(SAS)
25.【答案】(1)3
(2)解:如图3,连接AC、BD、AD,
∵AB是⊙O的直径,∴∠ADB=∠ACB=90 ,
∵AD =BD ,∴AD=BD,
∵AB=13,BC=12,∴由勾股定理得:AC=5,
由图1得:AC+BC= CD,5+12= CD,∴CD=
(3)解:解法一:以AB为直径作⊙O,连接DO并延长交⊙O于点D1,
连接D1A、D1B、D1C、CD,如图4,
由(2)得:AC+BC= D1C,∴D1C=2 ,
∵D1D是⊙O的直径,∴∠D1CD=90 ,
∵AC=m,BC=n,∴由勾股定理可求得:AB2=m2+n2,∴D1D2=AB2=m2+n2,
∵D1C2+DC2=D1D2,∴CD2=m2+n2 = ,
∵m解法二:如图5,∵∠ACB=∠DB=90 ,
∴A、B. C. D在以AB为直径的圆上,∴∠DAC=∠DBC,
将△BCD绕点D,逆时针旋转90 到△AED处,点B,C分别落在点A,E处,
∴△BCD≌△AED,∴CD=ED,∠ADC=∠ADE,
∴∠ADC ∠ADC=∠ADE ∠ADC,
即∠ADB=∠CDE=90 ,∴△CDE是等腰直角三角形,所以CE= CD,
∵AC=m,BC=n=AE,∴CE=n m,∴CD= .
【知识点】勾股定理;圆周角定理;旋转的性质;等腰直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【浙教版九上同步练习】
九上全册综合题一
一、单选题
1.下列说法正确的是( )
A.对角线相等的四边形是矩形
B.有两边及一角对应相等的两个三角形全等
C.对角线互相垂直的矩形是正方形
D.平分弦的直径垂直于弦
2.赵希的笔袋里装有5支同一品牌、同一型号的中性笔,其中有2支黑色,2支红色和1支蓝色,上课时,赵希随机的从笔袋中取出一只,若正好是黑色中性笔的概率是( )
A. B. C. D.
3.抛物线的 顶点坐标是( )
A. B. C. D.
4.如图,是二次函数的图象,则下列四个结论中正确的有( )
①;②;③;④.
A.1个 B.2个 C.3个 D.4个
5.二次函数的图象如图所示,则一次函数的图象大致是( )
A. B.
C. D.
6.如图,正方形ABCD边长为8,M,N分别是边BC,CD上的两个动点,且AM⊥MN,则AN的最小值是( )
A.8 B.4 C.10 D.8
二、填空题
7.抛物线的顶点坐标为 .
8.如图,在平面直角坐标系中,△ABC与△A'B'C是位似图形,位似中心是原点O,已知点A (2,a)、A' (4,b),则△ABC与△A' B' C'的相似比是
9.如果线段 , ,那么 和 的比例中项中 .
10.如图,扇形圆心角为直角,,点在上,以,为邻边构造菱形,边交于点,若,则图中两块阴影部分的面积和为 结果保留到
三、判断题
11.判断正误
(1)直径是圆的对称轴;
(2)平分弦的直径垂直于弦.
12.如图,转盘分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字.三位同学发表了下述见解,正确的在括号内打“√”,错误的打“×”.
(1)甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形.( )
(2)乙:只要指针连续转六次,一定会有一次停在6 号扇形. ( )
(3)丙:在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大.( )
13.圆的周长是直径的 π 倍.(判断对错)
14.判断对错。
比例尺是一个长度单位。
四、计算题
15.已知 ,求 的值。
16.计算:
(1).
(2)已知线段a=4,b=6,求线段a,b的比例中项c的长.
17.
(1)解方程:2x2+1=3x;
(2)将二次函数 配方成y=a(x﹣h)2+k的形式.
五、解答题
18.一个不透明的盒子中装有两个红球,一个白球和一个黄球,这些球除颜色外都相同,从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,请你用列表法或画树状图法求两次摸到的球的颜色都是红色的概率.
19.如图,在 中,点 , , 分别在 , , 上, , .若 , , ,求 的长.
20.小宇和小伟玩“石头、剪刀、布”的游戏.这个游戏的规则是:“剪刀”胜“布”,“布”胜“石头”,“石头”胜“剪刀”,手势相同不分胜负.如果二人同时随机出手(分别出三种手势中的一种手势)一次,那么小宇获胜的概率是多少?
六、作图题
21.如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(﹣2,3),B(﹣3,2),C(﹣1,1).
(1)以坐标原点O为位似中心,2为位似比.将△ABC放大,得到△A B C .请在平面直角坐标系中画出△A B C ;
(2)求出△A B C 的面积.
七、综合题
22.已知二次函数的图象经过点(0,3),顶点坐标为(1,4).
(1)求这个二次函数的解析式;
(2)若将该抛物线绕原点旋转180°,请直接写出旋转后的抛物线函数表达式。
23.一个布袋里装有4个只有颜色不同的球,其中3个红球,一个白球.从布袋里摸出一个球,记下颜色后放回,搅匀,再摸出1个球.求下列事件发生的概率:
(1)事件A:摸出一个红球,1个白球.
(2)事件B:摸出两个红球.
24.
(1)如图①,在 中, , 为 边上一点(不与点 , 重合),将线段 绕点 逆时针旋转90°得到 ,连接 ,试探索线段 , , 之间满足的等量关系,并证明你的结论.
(2)如图②,在 与 中, , ,将 绕点 旋转,使点 落在 边上,试探索线段 , , 之间满足的等量关系,并证明你的结论.
25.问题背景:如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC、BC、CD之间的数量关系.
小吴同学探究此问题的思路是:将ΔBCD绕点D逆时针旋转90°到ΔAED处,点B、C分别落在点A、E处(如图②),易证点C、A、E在同一条直线上,并且ΔCDE是等腰直角三角形,所以CE= CD,从而得出结论:AC+BC= CD.
图①
图②
图③
图④
简单应用:
(1)在图①中,若AC= ,BC=2 ,则CD= .
(2)如图③,AB是⊙O的直径,点C、D在⊙O上,弧AD=弧BD,若AB=13,BC=12,求CD的长.
(3)拓展延伸:
如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m
1.【答案】C
【知识点】三角形全等的判定;矩形的判定;正方形的性质;垂径定理
2.【答案】D
【知识点】概率公式
3.【答案】A
【知识点】二次函数y=a(x-h)^2+k的图象
4.【答案】C
【知识点】二次函数图象与系数的关系;二次函数y=ax^2+bx+c的性质
5.【答案】B
【知识点】二次函数图象与系数的关系;一次函数图象、性质与系数的关系
6.【答案】C
【知识点】二次函数的最值;相似三角形的判定与性质
7.【答案】(0,6)
【知识点】二次函数y=a(x-h)^2+k的图象
8.【答案】1:2
【知识点】位似变换
9.【答案】12
【知识点】比例的性质
10.【答案】
【知识点】菱形的性质;扇形面积的计算
11.【答案】(1)正确
(2)错误
【知识点】垂径定理
12.【答案】(1)错误
(2)错误
(3)错误
【知识点】事件发生的可能性
13.【答案】正确
【知识点】圆的认识
14.【答案】错误
【知识点】比例尺
15.【答案】解:∵ ,∴可设x=2k,则y=3k,z=5k
∴
【知识点】比例的性质
16.【答案】(1)解:原式
(2)解:解:由题意得,,a=4,b=6,,
∴.
【知识点】比例的性质;特殊角的三角函数值
17.【答案】(1)解:∵2x2﹣3x+1=0,
∴(2x﹣1)(x﹣1)=0,
解得:x1= ,x2=1;
(2)解: ,
,
= .
【知识点】因式分解法解一元二次方程;二次函数y=ax^2+bx+c与二次函数y=a(x-h)^2+k的转化
18.【答案】解:画树状图为:
共有12种等可能的结果数,两次摸到的球的颜色都是红色的结果数为2,
∴摸到的两个球的颜色都是红色的概率= .
【知识点】列表法与树状图法
19.【答案】解:∵ ,
∴
∵ , ,
∴
解得
【知识点】平行线分线段成比例
20.【答案】解:画树状图如下,
所有机会均等的情况共9种,小宇获胜的概率为:,
答:小宇获胜的概率是.
【知识点】列表法与树状图法;概率公式
21.【答案】(1)解:如图,△A'B'C'即为所求;
(2)解:△A'B'C的面积=4S△ABC=4(2×2﹣ ×1×1﹣ ×1×2﹣ ×1×2)=6.
【知识点】作图﹣位似变换
22.【答案】(1)解:设二次函数解析式为y=a(x﹣1)2+4,把点(0,3)代入得a+4=3,
解得:a=﹣1,∴这个二次函数解析式为y=﹣(x﹣1)2+4.
(2)解:y=(x+1)2-4
【知识点】二次函数图象的几何变换;待定系数法求二次函数解析式
23.【答案】(1)解:画树状图得:
∵共有16种等可能的结果,摸出一个红球,1个白球的有6种情况,
∴P(事件A)= = ;
(2)解:∵摸出两个红球的有9种情况,
∴P(事件B)= .
【知识点】列表法与树状图法;概率公式
24.【答案】(1)解: BC=DC+EC,证明如下:
∵将线段AD绕点A逆时针旋转90°得到AE,
∴AD=AE,∠DAE=90°,
∵∠BAC=∠DAE=90°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,
∴BC=DC+BD=DC+EC;
(2)BD2+CD2=2AD2,证明如下:
连接CE,
由(1)得,△BAD≌△CAE,
∴BD=CE,∠ACE=∠B,
∴∠DCE=90°,
∴CE2+CD2=ED2,
在Rt△ADE中,AD2+AE2=ED2,又AD=AE,
∴BD2+CD2=2AD2.
【知识点】旋转的性质;三角形全等的判定(SAS)
25.【答案】(1)3
(2)解:如图3,连接AC、BD、AD,
∵AB是⊙O的直径,∴∠ADB=∠ACB=90 ,
∵AD =BD ,∴AD=BD,
∵AB=13,BC=12,∴由勾股定理得:AC=5,
由图1得:AC+BC= CD,5+12= CD,∴CD=
(3)解:解法一:以AB为直径作⊙O,连接DO并延长交⊙O于点D1,
连接D1A、D1B、D1C、CD,如图4,
由(2)得:AC+BC= D1C,∴D1C=2 ,
∵D1D是⊙O的直径,∴∠D1CD=90 ,
∵AC=m,BC=n,∴由勾股定理可求得:AB2=m2+n2,∴D1D2=AB2=m2+n2,
∵D1C2+DC2=D1D2,∴CD2=m2+n2 = ,
∵m
∴A、B. C. D在以AB为直径的圆上,∴∠DAC=∠DBC,
将△BCD绕点D,逆时针旋转90 到△AED处,点B,C分别落在点A,E处,
∴△BCD≌△AED,∴CD=ED,∠ADC=∠ADE,
∴∠ADC ∠ADC=∠ADE ∠ADC,
即∠ADB=∠CDE=90 ,∴△CDE是等腰直角三角形,所以CE= CD,
∵AC=m,BC=n=AE,∴CE=n m,∴CD= .
【知识点】勾股定理;圆周角定理;旋转的性质;等腰直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
