第3章 圆的基本性质期末复习教案
图片预览



文档简介
《圆的基本性质》期末复习
一、圆的基本概念和垂径定理
1、圆的基本概念: 姓名:__________
(1)圆上任意两点间的部分叫做 。大于半圆的弧叫做 ,小于半圆的弧叫 ,
(2)连接圆上任意两点的线段叫做 ,经过圆心的弦叫 . .
(3)圆是 图形,其对称轴是任意一条 。
(4)下列说法正确的有( )
直径是圆的对称轴 B .半圆是弧 C. 半圆既不是优弧也不是劣弧
D. 直径是弦 E. 圆中两点间的部分为弦 F. 过圆上一点有无数条弦
2、垂径定理:垂直于弦的直径 这条弦,并且 弦所对的弧.
垂径定理的逆定理:平分弦( )的直径垂直 .
几何语言表示:如图,在⊙O中
例1、在直径650mm的圆柱形油槽中倒一些油后,截面如图。若油面宽AB=600mm,求油的最大深度。
同步练习:
1、 已知圆的半径为5,两平行弦长为6和8,则这两条弦的距离为 .
2、已知AB是半圆的直径,O是圆心,C是半圆上一点,OE交AC于D,AC=8,DE=2
OD = .
3、下列命题正确的是( )
A.弦的垂线平分弦所对的弧 B. 平分弦的直径垂直于这条弦
C. 过弦的中点的直线必过圆心
D. 弦所对的两条弧的中点连线垂直平分弦,且过圆心
如图已知⊙O的半径为30mm, 弦AB=36mm,点O到AB的距离是 。
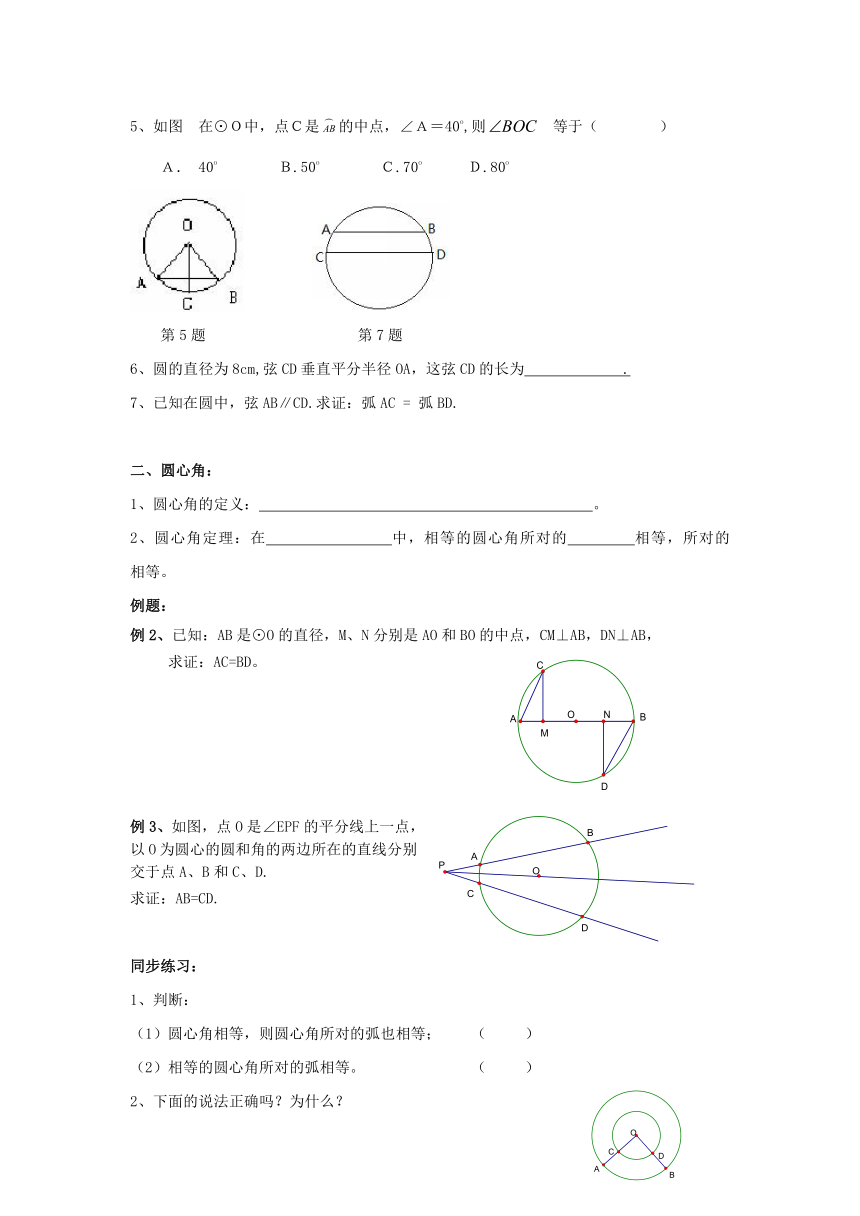
5、如图 在⊙O中,点C是的中点,∠A=40o,则等于( )
A. 40o B.50o C.70o D.80o
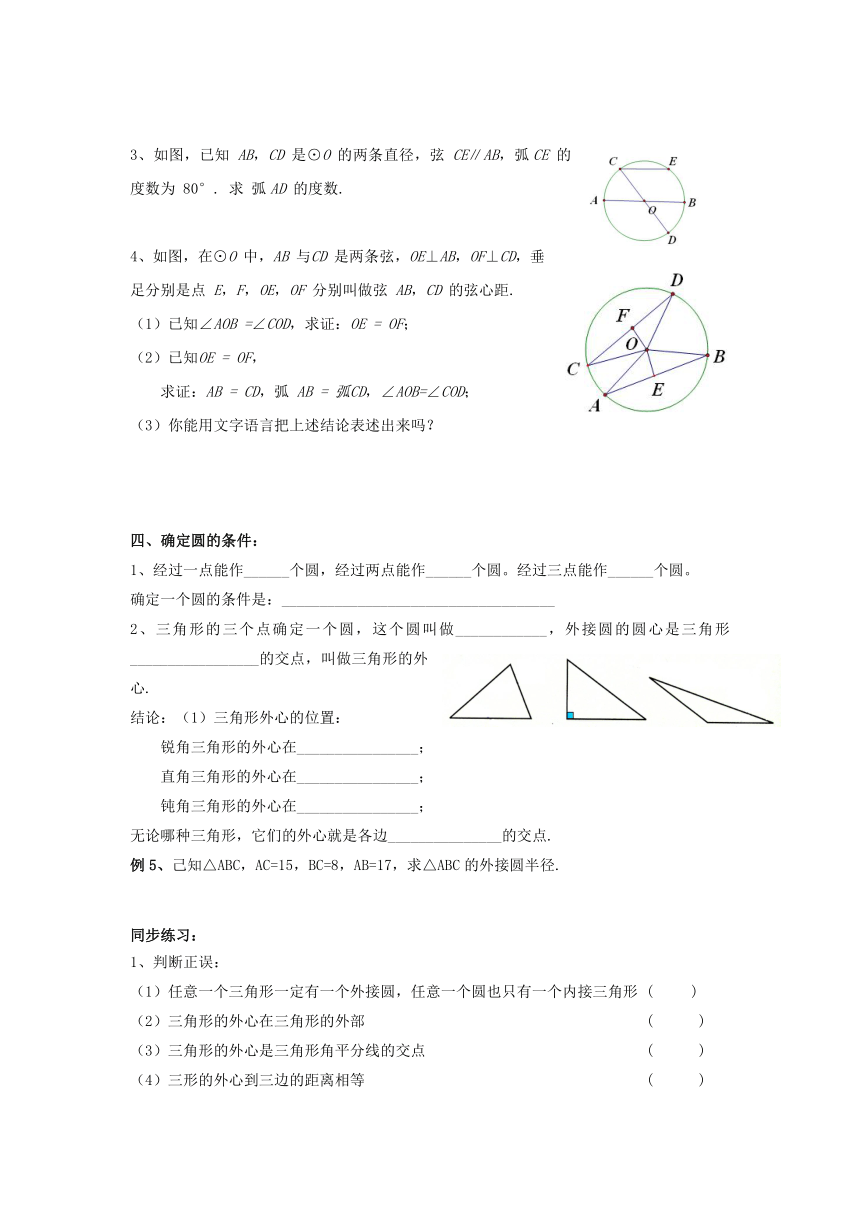
第5题 第7题
6、圆的直径为8cm,弦CD垂直平分半径OA,这弦CD的长为 .
7、已知在圆中,弦AB∥CD.求证:弧AC = 弧BD.
二、圆心角:
1、圆心角的定义: 。
2、圆心角定理:在 中,相等的圆心角所对的 相等,所对的 相等。
例题:
例2、已知:AB是⊙O的直径,M、N分别是AO和BO的中点,CM⊥AB,DN⊥AB,
求证:AC=BD。
例3、如图,点O是∠EPF的平分线上一点,以O为圆心的圆和角的两边所在的直线分别交于点A、B和C、D.
求证:AB=CD.
同步练习:
1、判断:
(1)圆心角相等,则圆心角所对的弧也相等; ( )
(2)相等的圆心角所对的弧相等。 ( )
2、下面的说法正确吗?为什么?
如图,因为∠AOB=∠COD,根据圆心角、弧、弦关系定理可知=。
3、如图,A、B、C、D是⊙O上的四个点,AB=DC,
求证:△ABC△DCB
4、如图,O为两个同圆的圆 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )心,大圆的弦AB交小圆于C、D两点,OE垂直于AB,垂足为E,若AC=2.5cm,ED=1.5cm,OA=5cm,则AB=
5、在⊙O中,弦AB=BC,求证:∠OAB=∠OCB。
三、圆心角的度数:
1、把顶点在圆心的周角等分成 份时,每一份的圆心角是1°的角。
2、因为在同圆中相等的圆心角所对的 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ) 相等,所以整个圆也被等分成360份,这时,把每一份这样得到的 叫做1°的弧。
3、n°的圆心角所对的弧是 的弧;n°的弧所对的圆心角是 的角
4、 圆心角与它所对的弧有以下关系:
圆心角的度数和它们对的弧的 相等。
例4、在⊙O 中,已知 AB 的度数为 120°,C 为 AB 的中点.
求证:四边形 OACB 是菱形.
同步练习:
1、 判断下列命题是真命题还是假命题:
(1)度数相等的弧所对的圆心角相等; ( )
(2)相等的圆心角所对弧的度数相等; ( )
(3)如果两条弧的度数相等,那么这两条弧也相等; ( )
(4)长度相等的弧的度数相等. ( )
2、 如图,在⊙O 中,∠B = 37°,劣弧 AB 的度数是多少?
3、如图,已知 AB,CD 是⊙O 的两条直径,弦 CE∥AB,弧CE 的度数为 80°. 求 弧AD 的度数.
4、如图,在⊙O 中,AB 与CD 是两条弦,OE⊥AB,OF⊥CD,垂足分别是点 E,F,OE,OF 分别叫做弦 AB,CD 的弦心距.
(1)已知∠AOB =∠COD,求证:OE = OF;
(2)已知OE = OF,
求证:AB = CD,弧 AB = 弧CD,∠AOB=∠COD;
你能用文字语言把上述结论表述出来吗?
四、确定圆的条件:
1、经过一点能作______个圆,经过两点能作______个圆。经过三点能作______个圆。
确定一个圆的条件是:____________________________________
2、三角形的三个点确定一个圆,这个圆叫 ( http: / / www.21cnjy.com )做____________,外接圆的圆心是三角形_________________的交点,叫做三角形的外心.
结论:(1)三角形外心的位置:
锐角三角形的外心在________________;
直角三角形的外心在________________;
钝角三角形的外心在________________;
无论哪种三角形,它们的外心就是各边_______________的交点.
例5、己知△ABC,AC=15,BC=8,AB=17,求△ABC的外接圆半径.
同步练习:
1、判断正误:
(1)任意一个三角形一定有一个外接圆,任意一个圆也只有一个内接三角形 ( )
(2)三角形的外心在三角形的外部 ( )
(3)三角形的外心是三角形角平分线的交点 ( )
(4)三形的外心到三边的距离相等 ( )
2、如图,A、B、C、表示三个村庄,现要建一座深水井泵站,向三个村庄分别送水,为使三条输水管线长度相同,请画出图,并说明理由.
3、己知点A、B,经过A、B作圆,则半径为2㎝的圆的个数为_____________个。
4、能在同一个圆上的是( )
A、平行四边形的四个顶点 B、菱形四边的中点
C、矩形四边的中点 D、正方形四边中点
5、己知A、B分别为∠MON边上异于O点的两点,则过A、O、B三点能作一个圆吗?
五、圆周角定理
1、圆周角是:___________________________________________
2、圆周角和圆心角的区别是:_____________________________________
3、圆周角定理:
推论 1: _______________________________________________________。
推论2: _____________________________________________________
例6、如图 ,AB 是⊙O 的直径, ( http: / / www.21cnjy.com )E 为⊙O 上的一点,C 是AE 的中点. CD⊥AB,垂足为点D, AE交CD于点F,连接AC.
求证:AF = CF .
同步练习:
1、下列各图中,是圆周角的是
2、 图3中有几个圆周角?( )(A)2个 (B)3个 (C)4个 (D)5个
( http: / / www.21cnjy.com )
3、 写出图4中的圆周角:_____________________________ .
4、如图5,在⊙O中,∠ABC=50°,则∠AOC等于( )
A、50°; B、80°; ( http: / / www.21cnjy.com ) C、90°; D、100°
5、如图6,△ABC的顶点A、B、C都在⊙O上,∠C=30 °,AB=2,则⊙O的半径是 .
6、如图7,圆心角∠AOB=100°,则∠ACB=__ _。
( http: / / www.21cnjy.com )
7、如图8,半径为R的圆中,有一弦分圆周成 ( http: / / www.21cnjy.com )1:2两部分,则弦所对的圆周角的度数是 . 8、如图9,圆周角∠ACB与∠ADB的关系?圆心角∠AOB是弧AB所对的.∠ACB、 ∠ADB、∠AOB有什么关系?如图,圆周角∠ACB与∠ADB的关系?圆心角∠AOB是弧AB所对的.∠ACB、 ∠ADB、∠AOB有什么关系?
9、填空题:
(1)、在圆中,一条弧所对的圆心角和圆周角 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )分别为(2x+100)°和(5x-30)°,则这条弧所对的圆心角和圆周角的度数分别为 .
(2)、如图,∠A是⊙O的圆周角,∠A=40°,则∠OBC= °.
10、判断题:
(1)等弧所对的圆周角相等; ( )
(2)相等的圆周角所对的弧也相等;( )
(3)90°的角所对的弦是直径; ( )
(4)同弦所对的圆周角相等. ( )
六、圆的内接四边形
1、___________________________叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
2、圆的内接四边形定理: _________________________________________________;
3*、圆的内接四边形定理的推论__________________________________________:
例7、圆内接四边形ABCD中,,则 .
同步练习:
1、下列关于圆内接四边形叙述正确的有
①圆内接四边形的任何一个外角都等于 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )它的内对角;②圆内接四边形对角相等;③圆内接四边形中不相邻的两个内角互补;④在圆内部的四边形叫圆内接四边形.
A.1个 B.2个 C.3个 D.4个
2、如图1,圆内接四边形ABCD中,,AC与BD交于点E,在下图中全等三角形的对数为
A.2对 B.3对 C.4对 D.5对
3、圆内接四边形ABCD中,,则圆的直径为
A.62 B.63 C.65 D.66
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图1 图2 图3
4、如图2,四边形ABCD为圆内接四边形,AC为BD的垂直平分线,,则
A. B. C. D.
5、如图3,圆内接四边形ABCD中,BA与CD的延长线交于点P,AC与BD交于点E,则图中相似三角形有
A.5对 B.4对 C.3对 D.2对
6、如图,已知圆内接四边形ABCD的边长为,则四边形ABCD面积为
A. B.8 C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
第6题 第7题 第10题
7、如图,在以BC为直径的半圆上任取一点P,过弧BP的中点A作于D.连接BP交AD于点E,交AC于点F,则
A.1:1 B.1:2 C.2:1 D.以上结论都不对
8、直线与与两坐标轴围成的四边形内接于一个圆,则实数
A.-3 B.3 C.-6 D.6
9、三角形三边长为5,12,13,则它的外接圆圆心到顶点的距离为 .
10、如图,AB为半圆O的直径,C、D为半圆上的两点,,则 .
11、已知:如图所示,平分.
(1)求AC和DB的长;
(2)求四边形ACBD的面积.
七、弧长和扇形面积计算:
如果扇形的圆心角是n°,半径是R,则:
1、弧长的计算公式: L= 。变形公式:R=_________;n=_________。
2、扇形的面积计算公式:S=_________=_____________。
变形公式:R=_________;n=_________。
例8、(1)如图,三个皮带轮的半径都是1,圆心距AC=3,BC=3.AB=6,则皮带的总长度为 .
(2)如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6,3,则图中阴影部分的面积是( )
A. B.
C. D.
同步练习:
1、填空:
(1)在半径为24的圆中,60°的圆心角所对的弧长为__ ___ .
(2)75°的圆心角所对的弧长是2.5π,则此弧所在圆的半径为 .
(3)若扇形的圆心角n为50°,半径为R=1,则这个扇形的面积S扇= .
(4)若扇形的圆心角n为60°, 面积为,则这个扇形的半径R= .
(5)若扇形的半径R=3, S扇形=3π,则这个扇形的圆心角n的度数为 .
(6)若扇形的半径R=2㎝,弧长㎝,则这个扇形的面积S扇= .
2、一条弧长等于,它的半径等于R,若这条弧所对的圆心角增加,则它的弧长增加( )
A. B. C. D.
3、如图,OA、OB、OC两两不相交,且半径都是2 cm,则图中三个扇形(阴影部分)的面积之和为 ( )
A.cm2 B. cm2 C. cm2 D.2 cm2
4、如图,△ABC是正三角形,曲线CDEF ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )……叫做“正三角形的渐开线”,其中弧CD、弧DE、弧EF……的圆心依次按A、B、C循环,它们依次相连结.若AB=1,那么曲线CDEF的长是( )
A.2 B.4 C.6 D.8
5、把一只折扇展开成一个扇形,它的圆心角为120°,半径为6,则这个扇形的弧长为 .
6、某市第三中学要修建一个圆心角为60°,半径为12米的扇形投掷场地,则该扇形场地的面积约为 ____ 米2. (取3.14,结果精确到0.1米2 )
7、如图,扇形AOB的圆心 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )角为直角,正方形OCDE内接于扇形.点C、E、D分别在OA、OB、弧AB上,过点A作AF⊥ED交ED的延长线于F,垂足为F.如果正方形的边长为1,那么阴影部分的面积为 .
8、如图,直线经过点M(1,)和点N(,3),A、B是此直线与坐标轴的交点.以AB为直径作⊙C,求此圆与y轴围成的阴影部分面积.
9、为庆祝祖国六十华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条、夹角为,的长为,贴布部分的长为,则贴布部分的面积约为____________.(取3)
P
O
B
A
一、圆的基本概念和垂径定理
1、圆的基本概念: 姓名:__________
(1)圆上任意两点间的部分叫做 。大于半圆的弧叫做 ,小于半圆的弧叫 ,
(2)连接圆上任意两点的线段叫做 ,经过圆心的弦叫 . .
(3)圆是 图形,其对称轴是任意一条 。
(4)下列说法正确的有( )
直径是圆的对称轴 B .半圆是弧 C. 半圆既不是优弧也不是劣弧
D. 直径是弦 E. 圆中两点间的部分为弦 F. 过圆上一点有无数条弦
2、垂径定理:垂直于弦的直径 这条弦,并且 弦所对的弧.
垂径定理的逆定理:平分弦( )的直径垂直 .
几何语言表示:如图,在⊙O中
例1、在直径650mm的圆柱形油槽中倒一些油后,截面如图。若油面宽AB=600mm,求油的最大深度。
同步练习:
1、 已知圆的半径为5,两平行弦长为6和8,则这两条弦的距离为 .
2、已知AB是半圆的直径,O是圆心,C是半圆上一点,OE交AC于D,AC=8,DE=2
OD = .
3、下列命题正确的是( )
A.弦的垂线平分弦所对的弧 B. 平分弦的直径垂直于这条弦
C. 过弦的中点的直线必过圆心
D. 弦所对的两条弧的中点连线垂直平分弦,且过圆心
如图已知⊙O的半径为30mm, 弦AB=36mm,点O到AB的距离是 。
5、如图 在⊙O中,点C是的中点,∠A=40o,则等于( )
A. 40o B.50o C.70o D.80o
第5题 第7题
6、圆的直径为8cm,弦CD垂直平分半径OA,这弦CD的长为 .
7、已知在圆中,弦AB∥CD.求证:弧AC = 弧BD.
二、圆心角:
1、圆心角的定义: 。
2、圆心角定理:在 中,相等的圆心角所对的 相等,所对的 相等。
例题:
例2、已知:AB是⊙O的直径,M、N分别是AO和BO的中点,CM⊥AB,DN⊥AB,
求证:AC=BD。
例3、如图,点O是∠EPF的平分线上一点,以O为圆心的圆和角的两边所在的直线分别交于点A、B和C、D.
求证:AB=CD.
同步练习:
1、判断:
(1)圆心角相等,则圆心角所对的弧也相等; ( )
(2)相等的圆心角所对的弧相等。 ( )
2、下面的说法正确吗?为什么?
如图,因为∠AOB=∠COD,根据圆心角、弧、弦关系定理可知=。
3、如图,A、B、C、D是⊙O上的四个点,AB=DC,
求证:△ABC△DCB
4、如图,O为两个同圆的圆 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )心,大圆的弦AB交小圆于C、D两点,OE垂直于AB,垂足为E,若AC=2.5cm,ED=1.5cm,OA=5cm,则AB=
5、在⊙O中,弦AB=BC,求证:∠OAB=∠OCB。
三、圆心角的度数:
1、把顶点在圆心的周角等分成 份时,每一份的圆心角是1°的角。
2、因为在同圆中相等的圆心角所对的 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 ) 相等,所以整个圆也被等分成360份,这时,把每一份这样得到的 叫做1°的弧。
3、n°的圆心角所对的弧是 的弧;n°的弧所对的圆心角是 的角
4、 圆心角与它所对的弧有以下关系:
圆心角的度数和它们对的弧的 相等。
例4、在⊙O 中,已知 AB 的度数为 120°,C 为 AB 的中点.
求证:四边形 OACB 是菱形.
同步练习:
1、 判断下列命题是真命题还是假命题:
(1)度数相等的弧所对的圆心角相等; ( )
(2)相等的圆心角所对弧的度数相等; ( )
(3)如果两条弧的度数相等,那么这两条弧也相等; ( )
(4)长度相等的弧的度数相等. ( )
2、 如图,在⊙O 中,∠B = 37°,劣弧 AB 的度数是多少?
3、如图,已知 AB,CD 是⊙O 的两条直径,弦 CE∥AB,弧CE 的度数为 80°. 求 弧AD 的度数.
4、如图,在⊙O 中,AB 与CD 是两条弦,OE⊥AB,OF⊥CD,垂足分别是点 E,F,OE,OF 分别叫做弦 AB,CD 的弦心距.
(1)已知∠AOB =∠COD,求证:OE = OF;
(2)已知OE = OF,
求证:AB = CD,弧 AB = 弧CD,∠AOB=∠COD;
你能用文字语言把上述结论表述出来吗?
四、确定圆的条件:
1、经过一点能作______个圆,经过两点能作______个圆。经过三点能作______个圆。
确定一个圆的条件是:____________________________________
2、三角形的三个点确定一个圆,这个圆叫 ( http: / / www.21cnjy.com )做____________,外接圆的圆心是三角形_________________的交点,叫做三角形的外心.
结论:(1)三角形外心的位置:
锐角三角形的外心在________________;
直角三角形的外心在________________;
钝角三角形的外心在________________;
无论哪种三角形,它们的外心就是各边_______________的交点.
例5、己知△ABC,AC=15,BC=8,AB=17,求△ABC的外接圆半径.
同步练习:
1、判断正误:
(1)任意一个三角形一定有一个外接圆,任意一个圆也只有一个内接三角形 ( )
(2)三角形的外心在三角形的外部 ( )
(3)三角形的外心是三角形角平分线的交点 ( )
(4)三形的外心到三边的距离相等 ( )
2、如图,A、B、C、表示三个村庄,现要建一座深水井泵站,向三个村庄分别送水,为使三条输水管线长度相同,请画出图,并说明理由.
3、己知点A、B,经过A、B作圆,则半径为2㎝的圆的个数为_____________个。
4、能在同一个圆上的是( )
A、平行四边形的四个顶点 B、菱形四边的中点
C、矩形四边的中点 D、正方形四边中点
5、己知A、B分别为∠MON边上异于O点的两点,则过A、O、B三点能作一个圆吗?
五、圆周角定理
1、圆周角是:___________________________________________
2、圆周角和圆心角的区别是:_____________________________________
3、圆周角定理:
推论 1: _______________________________________________________。
推论2: _____________________________________________________
例6、如图 ,AB 是⊙O 的直径, ( http: / / www.21cnjy.com )E 为⊙O 上的一点,C 是AE 的中点. CD⊥AB,垂足为点D, AE交CD于点F,连接AC.
求证:AF = CF .
同步练习:
1、下列各图中,是圆周角的是
2、 图3中有几个圆周角?( )(A)2个 (B)3个 (C)4个 (D)5个
( http: / / www.21cnjy.com )
3、 写出图4中的圆周角:_____________________________ .
4、如图5,在⊙O中,∠ABC=50°,则∠AOC等于( )
A、50°; B、80°; ( http: / / www.21cnjy.com ) C、90°; D、100°
5、如图6,△ABC的顶点A、B、C都在⊙O上,∠C=30 °,AB=2,则⊙O的半径是 .
6、如图7,圆心角∠AOB=100°,则∠ACB=__ _。
( http: / / www.21cnjy.com )
7、如图8,半径为R的圆中,有一弦分圆周成 ( http: / / www.21cnjy.com )1:2两部分,则弦所对的圆周角的度数是 . 8、如图9,圆周角∠ACB与∠ADB的关系?圆心角∠AOB是弧AB所对的.∠ACB、 ∠ADB、∠AOB有什么关系?如图,圆周角∠ACB与∠ADB的关系?圆心角∠AOB是弧AB所对的.∠ACB、 ∠ADB、∠AOB有什么关系?
9、填空题:
(1)、在圆中,一条弧所对的圆心角和圆周角 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )分别为(2x+100)°和(5x-30)°,则这条弧所对的圆心角和圆周角的度数分别为 .
(2)、如图,∠A是⊙O的圆周角,∠A=40°,则∠OBC= °.
10、判断题:
(1)等弧所对的圆周角相等; ( )
(2)相等的圆周角所对的弧也相等;( )
(3)90°的角所对的弦是直径; ( )
(4)同弦所对的圆周角相等. ( )
六、圆的内接四边形
1、___________________________叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
2、圆的内接四边形定理: _________________________________________________;
3*、圆的内接四边形定理的推论__________________________________________:
例7、圆内接四边形ABCD中,,则 .
同步练习:
1、下列关于圆内接四边形叙述正确的有
①圆内接四边形的任何一个外角都等于 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )它的内对角;②圆内接四边形对角相等;③圆内接四边形中不相邻的两个内角互补;④在圆内部的四边形叫圆内接四边形.
A.1个 B.2个 C.3个 D.4个
2、如图1,圆内接四边形ABCD中,,AC与BD交于点E,在下图中全等三角形的对数为
A.2对 B.3对 C.4对 D.5对
3、圆内接四边形ABCD中,,则圆的直径为
A.62 B.63 C.65 D.66
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
图1 图2 图3
4、如图2,四边形ABCD为圆内接四边形,AC为BD的垂直平分线,,则
A. B. C. D.
5、如图3,圆内接四边形ABCD中,BA与CD的延长线交于点P,AC与BD交于点E,则图中相似三角形有
A.5对 B.4对 C.3对 D.2对
6、如图,已知圆内接四边形ABCD的边长为,则四边形ABCD面积为
A. B.8 C. D.
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
第6题 第7题 第10题
7、如图,在以BC为直径的半圆上任取一点P,过弧BP的中点A作于D.连接BP交AD于点E,交AC于点F,则
A.1:1 B.1:2 C.2:1 D.以上结论都不对
8、直线与与两坐标轴围成的四边形内接于一个圆,则实数
A.-3 B.3 C.-6 D.6
9、三角形三边长为5,12,13,则它的外接圆圆心到顶点的距离为 .
10、如图,AB为半圆O的直径,C、D为半圆上的两点,,则 .
11、已知:如图所示,平分.
(1)求AC和DB的长;
(2)求四边形ACBD的面积.
七、弧长和扇形面积计算:
如果扇形的圆心角是n°,半径是R,则:
1、弧长的计算公式: L= 。变形公式:R=_________;n=_________。
2、扇形的面积计算公式:S=_________=_____________。
变形公式:R=_________;n=_________。
例8、(1)如图,三个皮带轮的半径都是1,圆心距AC=3,BC=3.AB=6,则皮带的总长度为 .
(2)如图,两同心圆的圆心为O,大圆的弦AB切小圆于P,两圆的半径分别为6,3,则图中阴影部分的面积是( )
A. B.
C. D.
同步练习:
1、填空:
(1)在半径为24的圆中,60°的圆心角所对的弧长为__ ___ .
(2)75°的圆心角所对的弧长是2.5π,则此弧所在圆的半径为 .
(3)若扇形的圆心角n为50°,半径为R=1,则这个扇形的面积S扇= .
(4)若扇形的圆心角n为60°, 面积为,则这个扇形的半径R= .
(5)若扇形的半径R=3, S扇形=3π,则这个扇形的圆心角n的度数为 .
(6)若扇形的半径R=2㎝,弧长㎝,则这个扇形的面积S扇= .
2、一条弧长等于,它的半径等于R,若这条弧所对的圆心角增加,则它的弧长增加( )
A. B. C. D.
3、如图,OA、OB、OC两两不相交,且半径都是2 cm,则图中三个扇形(阴影部分)的面积之和为 ( )
A.cm2 B. cm2 C. cm2 D.2 cm2
4、如图,△ABC是正三角形,曲线CDEF ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )……叫做“正三角形的渐开线”,其中弧CD、弧DE、弧EF……的圆心依次按A、B、C循环,它们依次相连结.若AB=1,那么曲线CDEF的长是( )
A.2 B.4 C.6 D.8
5、把一只折扇展开成一个扇形,它的圆心角为120°,半径为6,则这个扇形的弧长为 .
6、某市第三中学要修建一个圆心角为60°,半径为12米的扇形投掷场地,则该扇形场地的面积约为 ____ 米2. (取3.14,结果精确到0.1米2 )
7、如图,扇形AOB的圆心 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )角为直角,正方形OCDE内接于扇形.点C、E、D分别在OA、OB、弧AB上,过点A作AF⊥ED交ED的延长线于F,垂足为F.如果正方形的边长为1,那么阴影部分的面积为 .
8、如图,直线经过点M(1,)和点N(,3),A、B是此直线与坐标轴的交点.以AB为直径作⊙C,求此圆与y轴围成的阴影部分面积.
9、为庆祝祖国六十华诞,某单位排练的节目需用到如图所示的扇形布扇,布扇完全打开后,外侧两竹条、夹角为,的长为,贴布部分的长为,则贴布部分的面积约为____________.(取3)
P
O
B
A
同课章节目录
