6.2菱形(1)

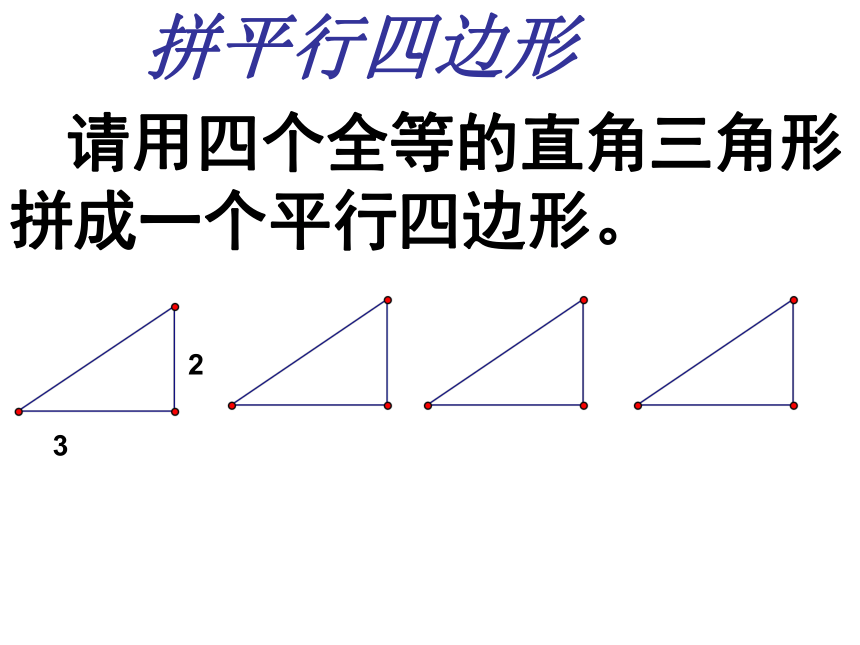
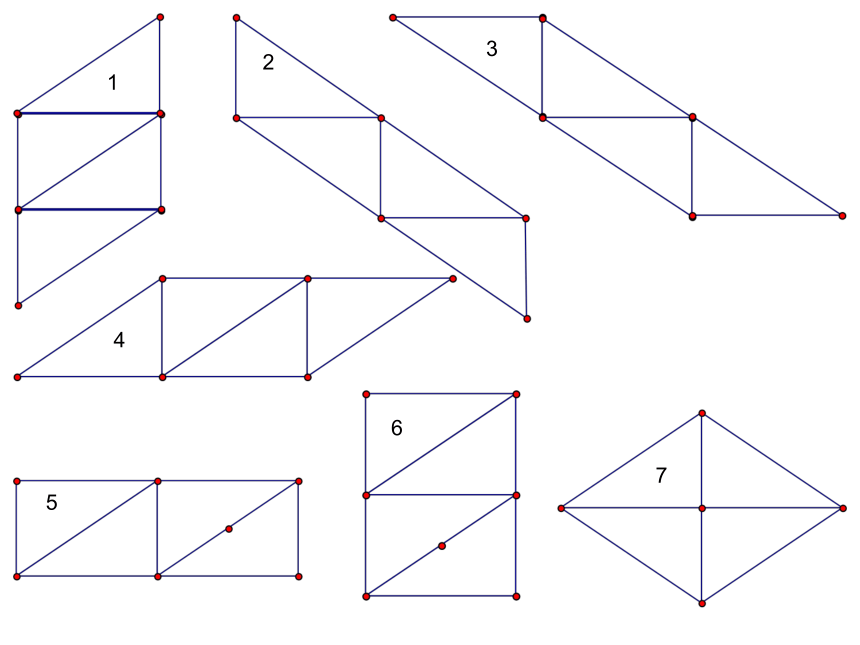
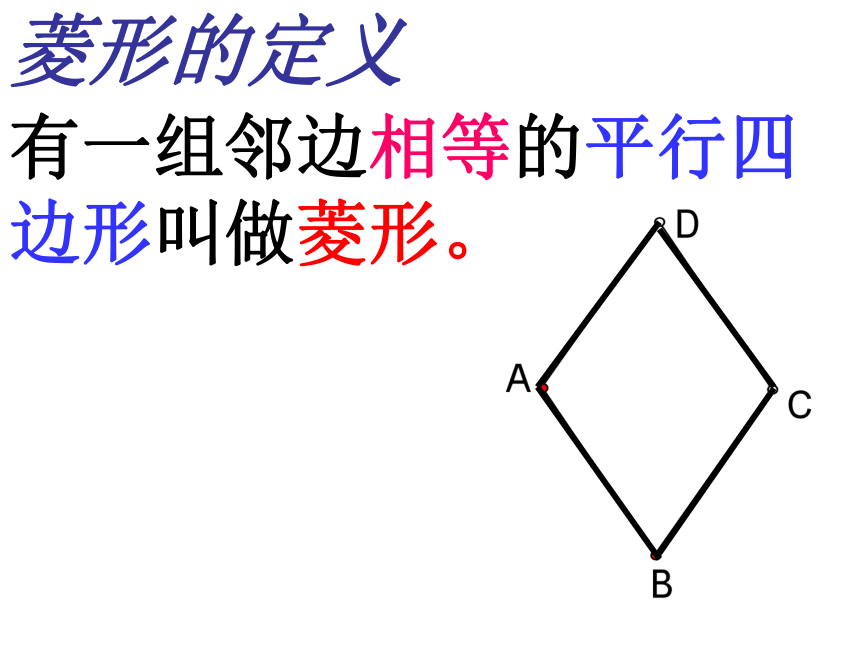
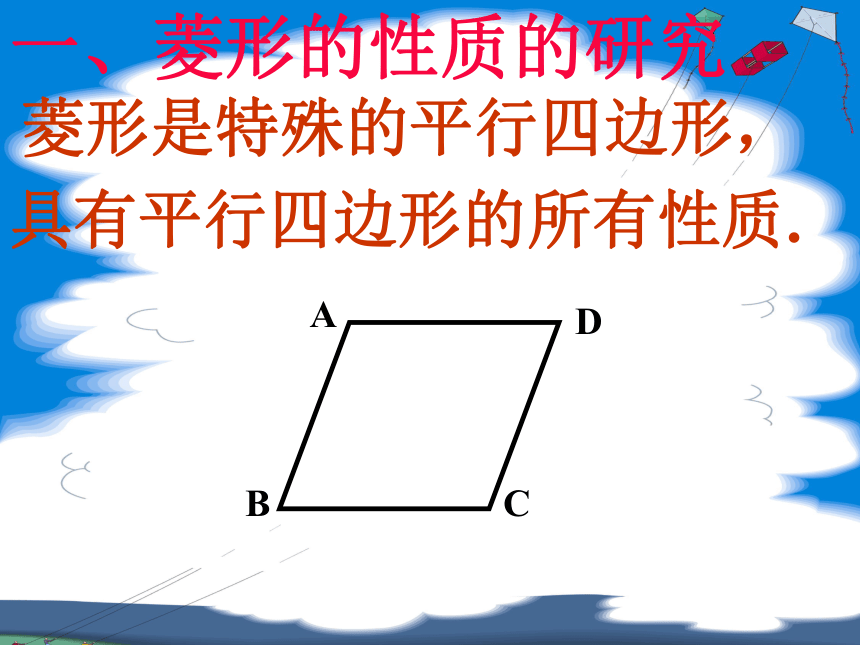
课件26张PPT。拼平行四边形 　请用四个全等的直角三角形拼成一个平行四边形。 2312356746.2 菱形(1)有一组邻边相等的平行四边形叫做菱形。菱形的定义菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.图片欣赏 菱形是特殊的平行四边形，
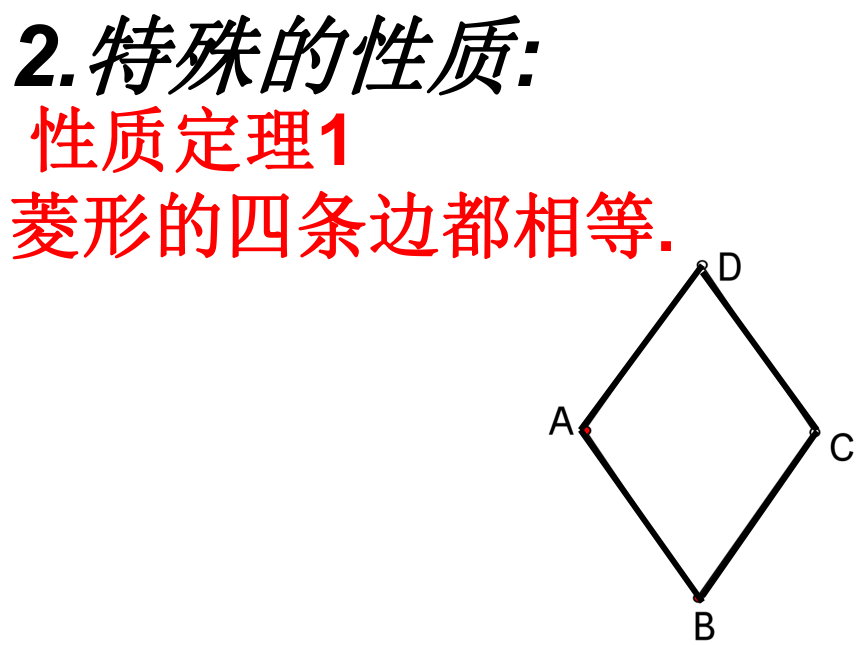
具有平行四边形的所有性质.一、菱形的性质的研究2.特殊的性质: 性质定理1
菱形的四条边都相等.2.特殊的性质: 性质定理2
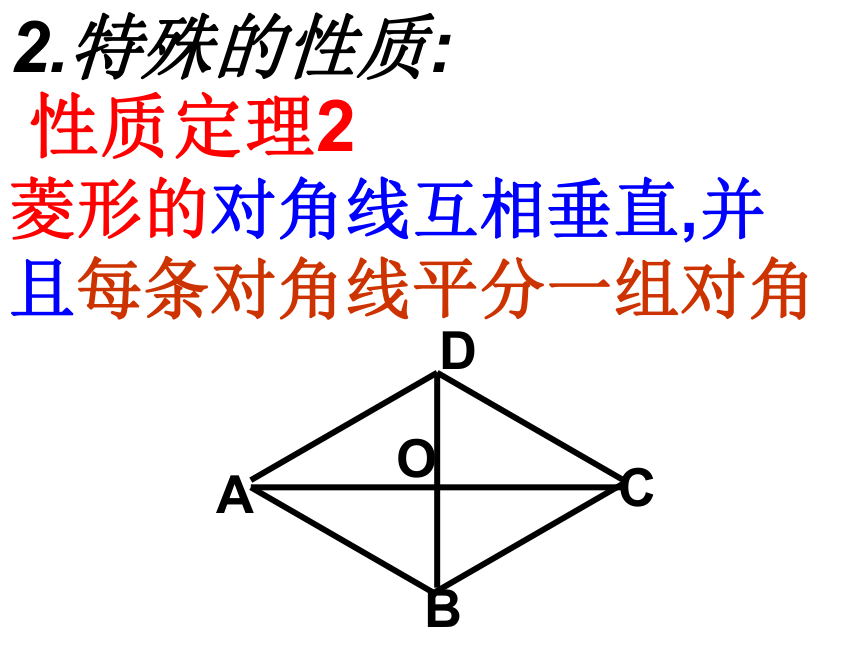
菱形的对角线互相垂直,并且每条对角线平分一组对角已知:在菱形ABCD中,对角线AC,BD相交于点O. 求证:AC⊥BD,AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC.想一想 菱形是不是轴对称图形？如果是轴对称图形，对称轴几条?菱形是轴对称图形，对称轴有两条。想一想 矩形是不是轴对称图形？如果是轴对称图形，对称轴几条?矩形、菱形都是轴对称图形，对称轴都有两条。例.如图,在菱形ABCD中,对角线AC,BD相交于点O, ∠OAB=30度, BD=6,求菱形的边长和对角线AC的长.AODBC【二、菱形的面积公式】　菱形是特殊的平行四边形,那么能否利用平行四边形面积公式计算菱形的面积吗?OES菱形=BC. AE 【二、菱形的面积公式】ABCDOS菱形=BC. AE思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗? 面积：S菱形=底×高=对角线乘积的一半相等的线段：相等的角：等腰三角形有：直角三角形有：全等三角形有：已知四边形ABCD是菱形AB=CD=AD=BC
OA=OC OB=OD∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8△ABC △ DBC △ACD △ABDRt△AOB Rt△BOC Rt△COD Rt△DOARt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACDABCDO12345678 轻松过关1.菱形具有而矩形不一定有的性质是 ( )
(A) 对角线互相平分 (B) 四条边都相等
(C) 对角相等 (D) 邻角互补2.已知:如图,在菱形ABCD中,直线AE交边BC于点E ，直线 AF交CD于点F。请你添加一个条件：
使得△ABE≌△ADF。３.在菱形ABCD中，AE⊥BC，AF⊥CD，E、F分别为BC，CD的中点，那么∠EAF的度数是（ ）A.75°B.60°C.45°D.30°B我来试试变式：在菱形ABCD中，E、F分别为BC、CD的中点，且AE⊥BC，AF⊥CD，求菱形各角的度数及∠EAF的度数。４、小试牛刀（2）已知：菱形ABCD中，对角线AC与BD相交于点O，且 AC=12，BD=16，则菱形ABCD的面积为 ，边长为 ，周长为 。（1）在菱形ABCD中，∠BAD=2∠B，则∠B= , △ABC是 三角形，∠ABD的度数为________ 。等边30 °96104060 °C ５．如图，在一种可伸缩的衣帽架中，每个菱形的周长都为100厘米，固定在墙上的两点A、B之间的距离为25厘米，则∠ACB= .AB6．菱形ABCD的周长为16，相邻两角的度数比为1：2．⑴求菱形ABCD的对角线的长；⑵求菱形ABCD的面积．7．已知如图，菱形ABCD中，E是AB的中点，且DE⊥AB，AB=1。
求（1）∠ABC的度数；
（2）对角线AC、BD的长；
（3）菱形ABCD的面积。９.菱形ABCD中∠ABC=60°,AB=4cm,P为BD上任意一点,E为BC中点,求PE+PC的最小值.挑战自我已知,在菱形ABCD中,∠BAD=120度 现将一块含６０度角的三角尺AMN(其中∠NAM=６０度)叠放在菱形上,然后将三角尺绕点A旋转.在旋转过程中,设AM交边BC于点E,AN交边CD于点F,那么BE+DF与AB有着怎样的数量关系?菱形的性质:1.菱形是特殊的平行四边形,具有一般平行四边形的所有性质.(1) 性质1 菱形的四条边都相等.(2) 性质2 菱形的对角线互相垂直,并且每条对角线平分一组对角.(3) 菱形是轴对称图形,它的对称轴是对角线所在的直线.