2023-2024学年浙教版数学八年级上册第1章三角形的初步知识单元知识点专练(含答案)
文档属性
| 名称 | 2023-2024学年浙教版数学八年级上册第1章三角形的初步知识单元知识点专练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 206.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-22 00:00:00 | ||
图片预览


文档简介
浙教版数学八年级上册单元知识点专练
第1章 三角形的初步知识
类型之一 定义与命题
1.下列命题是假命题的是 ( )
A.三边对应相等的两个三角形全等
B.等角的补角相等
C.角平分线上的点到角两边的距离相等
D.同位角相等
2.下列选项中,可以用来说明命题“若a2>b2,则a>b”是假命题的反例是 ( )
A.a=3,b=-2 B.a=2,b=1
C.a=-3,b=2 D.a=-2,b=3
类型之二 三角形的高线、中线与角平分线
3.如图1-X-1,在△ABC中,已知D,E,F分别是BC,AD,CE的中点,且△ABC的面积是8,则△BEF的面积是 ( )
A.2 B.1 C.4 D.3
图1-X-1
4.如图1-X-2,在△ABC中,∠BAC=56°,BP,CP分别平分∠ABC和∠ACB,则∠BPC的度数为 ( )
A.122° B.118° C.148° D.140°
图1-X-2
类型之三 三角形的三边关系
5.若三角形的两边长分别为2,6,则该三角形的第三边长可能是 ( )
A.3 B.4 C.5 D.9
类型之四 三角形的角的关系
6.在△ABC中,若∠A=∠C-∠B,则△ABC是 ( )
A.锐角三角形 B.钝角三角形
C.等腰三角形 D.直角三角形
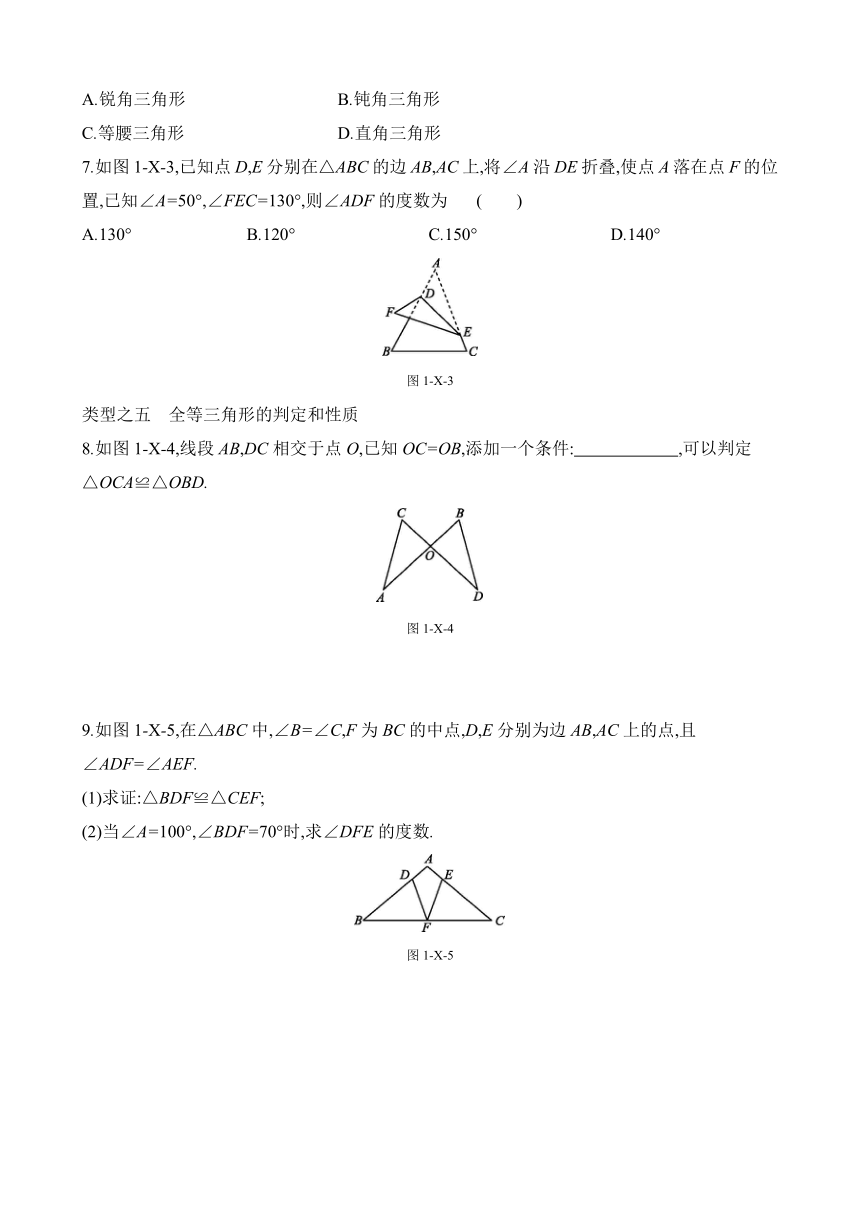
7.如图1-X-3,已知点D,E分别在△ABC的边AB,AC上,将∠A沿DE折叠,使点A落在点F的位置,已知∠A=50°,∠FEC=130°,则∠ADF的度数为 ( )
A.130° B.120° C.150° D.140°
图1-X-3
类型之五 全等三角形的判定和性质
8.如图1-X-4,线段AB,DC相交于点O,已知OC=OB,添加一个条件: ,可以判定△OCA≌△OBD.
图1-X-4
9.如图1-X-5,在△ABC中,∠B=∠C,F为BC的中点,D,E分别为边AB,AC上的点,且∠ADF=∠AEF.
(1)求证:△BDF≌△CEF;
(2)当∠A=100°,∠BDF=70°时,求∠DFE的度数.
图1-X-5
类型之六 角平分线、线段垂直平分线的性质
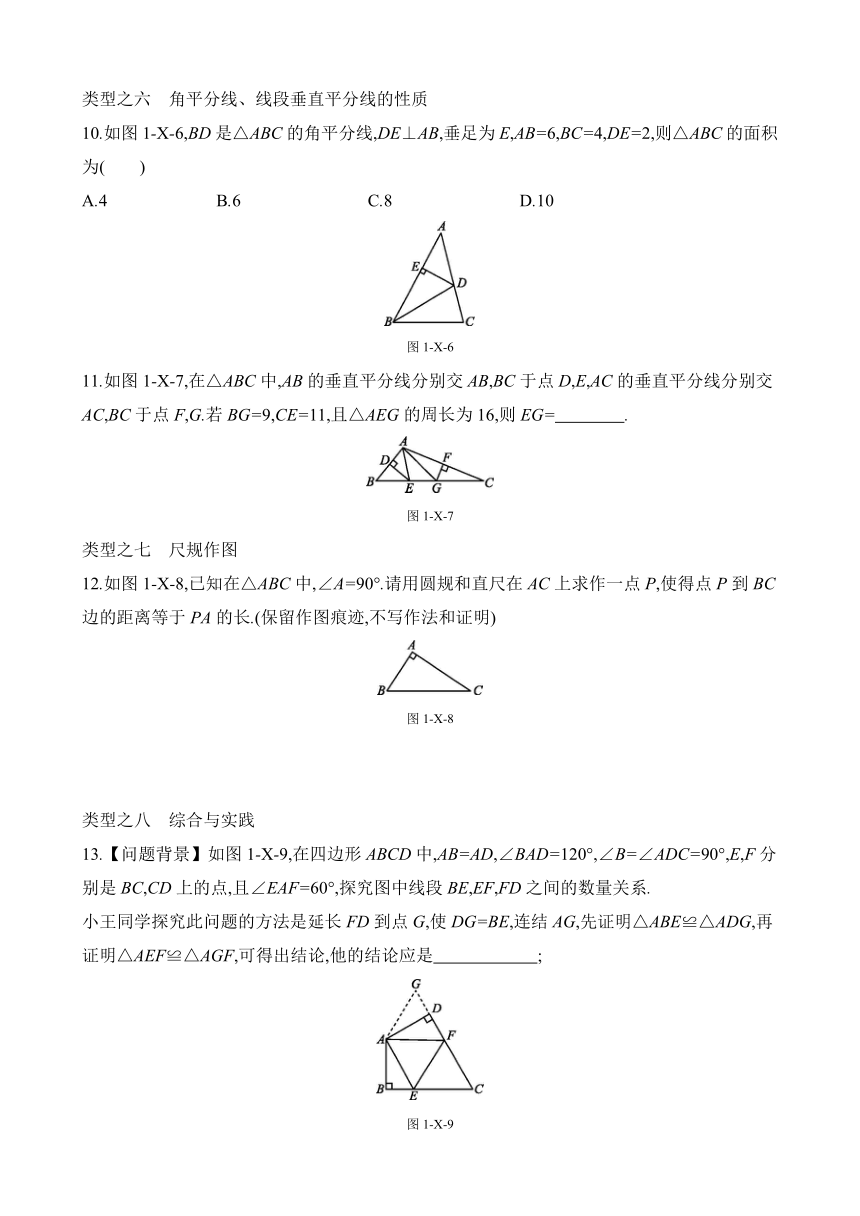
10.如图1-X-6,BD是△ABC的角平分线,DE⊥AB,垂足为E,AB=6,BC=4,DE=2,则△ABC的面积为( )
A.4 B.6 C.8 D.10
图1-X-6
11.如图1-X-7,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,AC的垂直平分线分别交AC,BC于点F,G.若BG=9,CE=11,且△AEG的周长为16,则EG= .
图1-X-7
类型之七 尺规作图
12.如图1-X-8,已知在△ABC中,∠A=90°.请用圆规和直尺在AC上求作一点P,使得点P到BC边的距离等于PA的长.(保留作图痕迹,不写作法和证明)
图1-X-8
类型之八 综合与实践
13.【问题背景】如图1-X-9,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
图1-X-9
【探索延伸】如图1-X-10,若在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立 请说明理由;
图1-X-10
【实际应用】如图1-X-11,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲沿正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角∠EOF为70°,则此时两舰艇之间的距离EF为 .
图1-X-11
【答案解析】
1.D [解析] A项,三边对应相等的两个三角形全等,正确,是真命题;B项,等角的补角相等,正确,是真命题;C项,角平分线上的点到角两边的距离相等,正确,是真命题;D项,两直线平行,同位角相等,故该命题是假命题.故选D.
2.C
3.A [解析] ∵F是CE的中点,
∴S△BEF=S△BEC.
同理可得S△BED=S△ABD,S△CDE=S△ACD,
∴S△BED+S△CDE=S△ABD+S△ACD,
即S△BEC=S△ABC,
∴S△BEF=S△ABC.
又∵S△ABC=8,
∴S△BEF=2,
即△BEF的面积为2.故选A.
4.B
5.C
6.D [解析] ∵∠A=∠C-∠B,
∴∠A+∠B=∠C.
∵∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形.
故选D.
7.C
8.答案不唯一,如OA=OD
9.解:(1)证明:∵∠ADF=∠AEF,
∴∠BDF=∠CEF.
∵F为BC的中点,
∴BF=CF.
在△BDF与△CEF中,
∵
∴△BDF≌△CEF(AAS).
(2)∵∠A=100°,
∴∠B=∠C=40°.
又∵∠BDF=70°,
∴∠BFD=70°.
∵△BDF≌△CEF,
∴∠CFE=∠BFD=70°,
∴∠DFE=180°-∠BFD-∠CFE=180°-70°-70°=40°.
10.D [解析] 过点D作DF⊥BC于点F,如图.
∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,
∴DF=DE=2,
∴S△ABC=S△ABD+S△BCD
=×6×2+×4×2
=10.
故选D.
11.4 [解析] ∵DE是AB的垂直平分线,FG是AC的垂直平分线,
∴AE=BE,AG=CG.
∵△AEG的周长为16,
∴AE+EG+AG=16,
∴BE+EG+CG=16,
∴BC=16.
∵BG=9,CE=11,
∴EG=BG+CE-BC=4.
故答案为4.
12.解:如图,点P即为所求.
13.解:【问题背景】EF=BE+FD
【探索延伸】EF=BE+FD仍然成立.
理由:延长FD到点G,使DG=BE,连结AG.
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,
∴∠B=∠ADG.
在△ABE和△ADG中,
∵
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG.
∵∠EAF=∠BAD,
∴∠GAF=∠FAD+∠DAG=∠FAD+∠BAE=∠BAD-∠EAF=∠BAD-∠BAD=∠BAD,
∴∠EAF=∠GAF.
在△AEF和△AGF中,∵
∴△AEF≌△AGF(SAS),∴EF=GF.
又∵GF=DG+FD=BE+FD,
∴EF=BE+FD.
【实际应用】210海里 [解析] 如图,连结EF,延长AE,BF交于点C.
在四边形AOBC中,
由题意,易得∠AOB=30°+90°+20°=140°,
∠EOF=70°=∠AOB,且OA=OB,∠OAC+∠OBC=60°+120°=180°,符合【探索延伸】中的条件,
∴结论EF=AE+BF成立,
即EF=AE+BF=1.5×(60+80)=210(海里).
故答案为210海里.
第1章 三角形的初步知识
类型之一 定义与命题
1.下列命题是假命题的是 ( )
A.三边对应相等的两个三角形全等
B.等角的补角相等
C.角平分线上的点到角两边的距离相等
D.同位角相等
2.下列选项中,可以用来说明命题“若a2>b2,则a>b”是假命题的反例是 ( )
A.a=3,b=-2 B.a=2,b=1
C.a=-3,b=2 D.a=-2,b=3
类型之二 三角形的高线、中线与角平分线
3.如图1-X-1,在△ABC中,已知D,E,F分别是BC,AD,CE的中点,且△ABC的面积是8,则△BEF的面积是 ( )
A.2 B.1 C.4 D.3
图1-X-1
4.如图1-X-2,在△ABC中,∠BAC=56°,BP,CP分别平分∠ABC和∠ACB,则∠BPC的度数为 ( )
A.122° B.118° C.148° D.140°
图1-X-2
类型之三 三角形的三边关系
5.若三角形的两边长分别为2,6,则该三角形的第三边长可能是 ( )
A.3 B.4 C.5 D.9
类型之四 三角形的角的关系
6.在△ABC中,若∠A=∠C-∠B,则△ABC是 ( )
A.锐角三角形 B.钝角三角形
C.等腰三角形 D.直角三角形
7.如图1-X-3,已知点D,E分别在△ABC的边AB,AC上,将∠A沿DE折叠,使点A落在点F的位置,已知∠A=50°,∠FEC=130°,则∠ADF的度数为 ( )
A.130° B.120° C.150° D.140°
图1-X-3
类型之五 全等三角形的判定和性质
8.如图1-X-4,线段AB,DC相交于点O,已知OC=OB,添加一个条件: ,可以判定△OCA≌△OBD.
图1-X-4
9.如图1-X-5,在△ABC中,∠B=∠C,F为BC的中点,D,E分别为边AB,AC上的点,且∠ADF=∠AEF.
(1)求证:△BDF≌△CEF;
(2)当∠A=100°,∠BDF=70°时,求∠DFE的度数.
图1-X-5
类型之六 角平分线、线段垂直平分线的性质
10.如图1-X-6,BD是△ABC的角平分线,DE⊥AB,垂足为E,AB=6,BC=4,DE=2,则△ABC的面积为( )
A.4 B.6 C.8 D.10
图1-X-6
11.如图1-X-7,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,AC的垂直平分线分别交AC,BC于点F,G.若BG=9,CE=11,且△AEG的周长为16,则EG= .
图1-X-7
类型之七 尺规作图
12.如图1-X-8,已知在△ABC中,∠A=90°.请用圆规和直尺在AC上求作一点P,使得点P到BC边的距离等于PA的长.(保留作图痕迹,不写作法和证明)
图1-X-8
类型之八 综合与实践
13.【问题背景】如图1-X-9,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
图1-X-9
【探索延伸】如图1-X-10,若在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立 请说明理由;
图1-X-10
【实际应用】如图1-X-11,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲沿正东方向以60海里/时的速度前进,舰艇乙沿北偏东50°的方向以80海里/时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角∠EOF为70°,则此时两舰艇之间的距离EF为 .
图1-X-11
【答案解析】
1.D [解析] A项,三边对应相等的两个三角形全等,正确,是真命题;B项,等角的补角相等,正确,是真命题;C项,角平分线上的点到角两边的距离相等,正确,是真命题;D项,两直线平行,同位角相等,故该命题是假命题.故选D.
2.C
3.A [解析] ∵F是CE的中点,
∴S△BEF=S△BEC.
同理可得S△BED=S△ABD,S△CDE=S△ACD,
∴S△BED+S△CDE=S△ABD+S△ACD,
即S△BEC=S△ABC,
∴S△BEF=S△ABC.
又∵S△ABC=8,
∴S△BEF=2,
即△BEF的面积为2.故选A.
4.B
5.C
6.D [解析] ∵∠A=∠C-∠B,
∴∠A+∠B=∠C.
∵∠A+∠B+∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形.
故选D.
7.C
8.答案不唯一,如OA=OD
9.解:(1)证明:∵∠ADF=∠AEF,
∴∠BDF=∠CEF.
∵F为BC的中点,
∴BF=CF.
在△BDF与△CEF中,
∵
∴△BDF≌△CEF(AAS).
(2)∵∠A=100°,
∴∠B=∠C=40°.
又∵∠BDF=70°,
∴∠BFD=70°.
∵△BDF≌△CEF,
∴∠CFE=∠BFD=70°,
∴∠DFE=180°-∠BFD-∠CFE=180°-70°-70°=40°.
10.D [解析] 过点D作DF⊥BC于点F,如图.
∵BD是△ABC的角平分线,DE⊥AB,DF⊥BC,
∴DF=DE=2,
∴S△ABC=S△ABD+S△BCD
=×6×2+×4×2
=10.
故选D.
11.4 [解析] ∵DE是AB的垂直平分线,FG是AC的垂直平分线,
∴AE=BE,AG=CG.
∵△AEG的周长为16,
∴AE+EG+AG=16,
∴BE+EG+CG=16,
∴BC=16.
∵BG=9,CE=11,
∴EG=BG+CE-BC=4.
故答案为4.
12.解:如图,点P即为所求.
13.解:【问题背景】EF=BE+FD
【探索延伸】EF=BE+FD仍然成立.
理由:延长FD到点G,使DG=BE,连结AG.
∵∠B+∠ADC=180°,∠ADG+∠ADC=180°,
∴∠B=∠ADG.
在△ABE和△ADG中,
∵
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG.
∵∠EAF=∠BAD,
∴∠GAF=∠FAD+∠DAG=∠FAD+∠BAE=∠BAD-∠EAF=∠BAD-∠BAD=∠BAD,
∴∠EAF=∠GAF.
在△AEF和△AGF中,∵
∴△AEF≌△AGF(SAS),∴EF=GF.
又∵GF=DG+FD=BE+FD,
∴EF=BE+FD.
【实际应用】210海里 [解析] 如图,连结EF,延长AE,BF交于点C.
在四边形AOBC中,
由题意,易得∠AOB=30°+90°+20°=140°,
∠EOF=70°=∠AOB,且OA=OB,∠OAC+∠OBC=60°+120°=180°,符合【探索延伸】中的条件,
∴结论EF=AE+BF成立,
即EF=AE+BF=1.5×(60+80)=210(海里).
故答案为210海里.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
