3.8弧长及扇形面积 浙教版初中数学九年级上册同步练习(含详细答案解析)
文档属性
| 名称 | 3.8弧长及扇形面积 浙教版初中数学九年级上册同步练习(含详细答案解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 805.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-24 12:35:41 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
3.8弧长及扇形面积浙教版初中数学九年级上册同步练习
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.用一个圆心角为,半径为的扇形作一个圆锥的侧面,则这个圆锥的底面直径是( )
A. B. C. D.
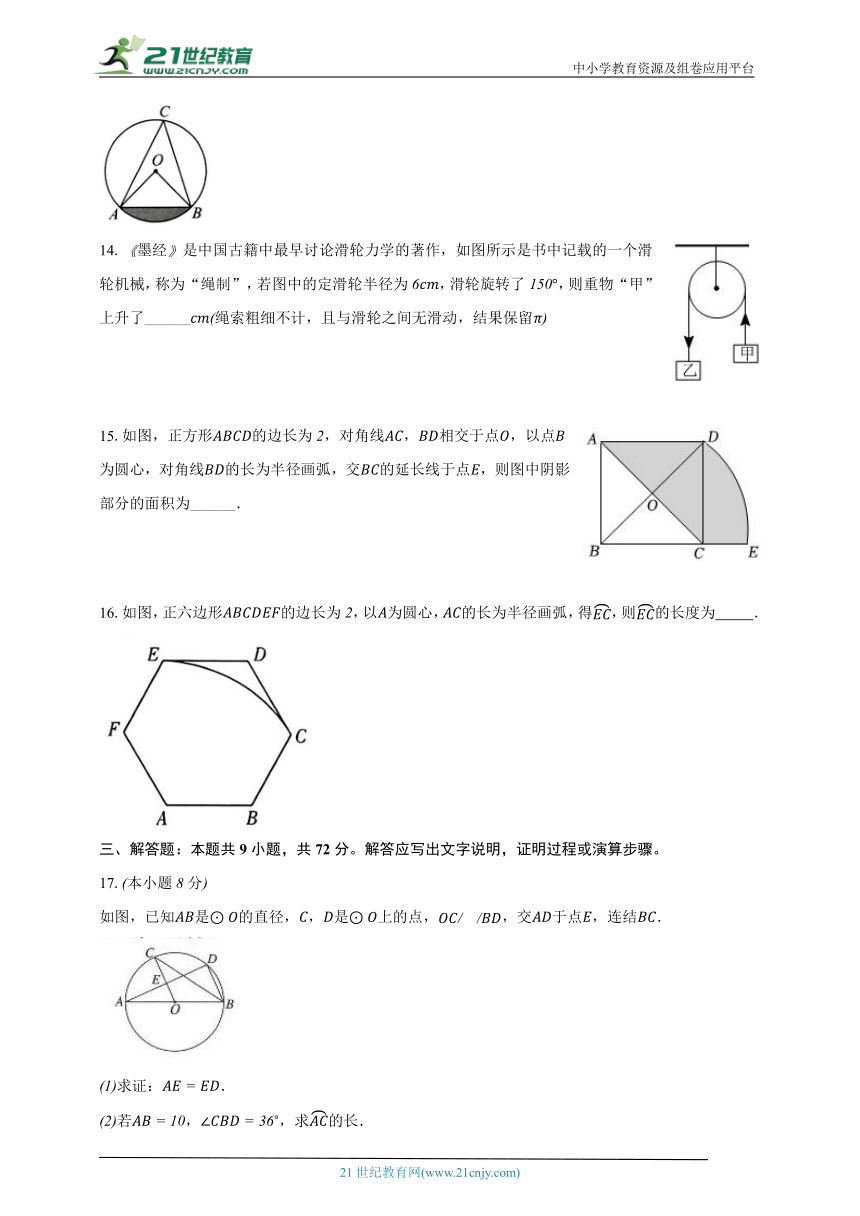
2.一个滑轮起重装置如图所示,滑轮的半径是,当重物上升时,滑轮的一条半径绕轴心按顺时针方向旋转的角度约为 取,结果精确到
A. B. C. D.
3.如图,在扇形中,,半径,将扇形沿过点的直线折叠,点恰好落在上的点处,折痕交于点,则阴影部分的面积为( )
A. B. C. D.
4.如图,点是直径为的半圆的中点,连接,分别以点和为圆心,以大于的长为半径作弧,两弧相交于点,作直线交于点,连接,则阴影部分的面积为( )
A. B. C. D.
5.如图,在扇形中,,,若弦,则的长为( )
A.
B.
C.
D.
6.如图,在正方形中,边长,将正方形绕点按逆时针方向旋转至正方形,则线段扫过的面积为( )
A.
B.
C.
D.
7.如图,是半径为的半圆上的两个点,是直径,,若的长度为,则图中阴影部分的面积为
A. B. C. D.
8.如图,在中,,以为直径的与,分别交于点,,连接,,若,,则阴影部分的面积为( )
A. B. C. D.
9.如图,将扇形沿方向平移,使点移到的中点处,得到扇形若,,则阴影部分的面积为( )
A. B. C. D.
10.如图,一条公路的转弯处是一段圆弧,点是这段弧所在圆的圆心,为上一点,于若,,则的长为( )
A. B. C. D.
11.如图,扇形纸片的半径为,沿折叠扇形纸片,点恰好落在上的点处,图中阴影部分的面积为( )
A. B. C. D.
12.如图,为圆的直径,点在圆上,若,,则的长为
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.如图,在中,,,则图中阴影部分的面积为 .
14.墨经是中国古籍中最早讨论滑轮力学的著作,如图所示是书中记载的一个滑轮机械,称为“绳制”,若图中的定滑轮半径为,滑轮旋转了,则重物“甲”上升了______绳索粗细不计,且与滑轮之间无滑动,结果保留
15.如图,正方形的边长为,对角线,相交于点,以点为圆心,对角线的长为半径画弧,交的延长线于点,则图中阴影部分的面积为______.
16.如图,正六边形的边长为,以为圆心,的长为半径画弧,得,则的长度为 .
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
如图,已知是的直径,,是上的点,,交于点,连结.
求证:.
若,,求的长.
18.本小题分
已知:的直径,与相交于点、,的直径与相交于点,设的半径为,的长为,
如图,当点在线段上时,求关于的函数解析式,并写出定义域;
当点在直径上时,如果的长为,求公共弦的长;
设与相交于,试问能否为等腰三角形?如果能够,请直接写出的长度不必写过程;如果不能,请简要说明理由.
19.本小题分
如图所示,矩形的边在轴上,在轴上,点的坐标是,反比例函数的图象经过点,以点为圆心,为半径作交边于点,连接.
求反比例函数的解析式.
求的度数.
请直接写出图中阴影部分的面积.
20.本小题分
如图,的顶点坐标分别为,,画出将绕点旋转后的,并求旋转过程中点经过的路线长.
21.本小题分
如图,在中,弦垂直于半径,垂足为点点是优弧上一点,连接,,,.
求的度数.
若,求图中劣弧的长.
22.本小题分
如图,在平面直角坐标系中,已知的三个顶点坐标分别是,.
将向上平移个单位,再向右平移个单位,得到,请画出;
请画出关于轴对称的;
将绕着原点顺时针旋转,得到,求线段在旋转过程中扫过的面积结果保留.
23.本小题分
学习下面方框内的内容,并解答下列问题:
小明在反思学习时,发现解决下列个问题时都用到了同一种数学思想方法:
问题若,求的值.
解决思路:.
问题如图,分别以的个顶点为圆心,为半径画圆,求图中块阴影面积之和.
解决思路:将块阴影扇形拼成一个半径为的半圆,则阴影面积为.
问题已知,求的值.
解题思路:对已知条件进行恒等变形,,,因为,所以,类似可以得到.
问题:
方框内个问题的解决都用到了 的数学思想方法从下列选项中选一个
A.分类讨论
B.数形结合
C.整体
D.从特殊到一般
方框内问题中的值为
如图,已知的半径为,、是的弦,且,,求与的长度之和.
24.本小题分
如图,平面直角坐标系中,的顶点都在正方形每个小正方形边长为单位网格的格点上.
的形状是______直接写答案
画出沿轴翻折后的;
画出绕点顺时针旋转的并求出旋转过程中扫过的面积.结果保留
25.本小题分
如图,网格中每个小正方形的边长均为个单位长度,的顶点均在小正方形的格点上.
将向下平移个单位长度得到,画出;
将绕点按顺时针方向旋转得到,画出;
在的条件下,请求出线段在旋转过程中扫过的面积.
答案和解析
1.【答案】
【解析】【分析】
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.根据弧长公式先计算出扇形的弧长,再利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长求解.
【解答】
解:扇形的弧长,
设圆锥的底面直径为,则,
所以.
2.【答案】
【解析】【分析】
本题考查了弧长的计算公式:,其中表示弧长,表示弧所对的圆心角的度数.
重物上升,说明点转过的路径长为,然后根据弧长公式得到的方程,解方程即可.
【解答】
解:根据题意得,,
解得,,
所以绕轴心按逆时针方向旋转的角度约为.
故选:.
3.【答案】
【解析】解:连接,交于,
沿对折和重合,,
,,,,
,是等边三角形,
,
,
,
,
,
阴影部分的面积
,
故选:.
连接,交于,根据对折得出,,,,得出是等边三角形,根据等边三角形的性质得出,求出,求出,再分别求出扇形和的面积即可.
本题考查了等边三角形的性质和判定,直角三角形的性质,扇形的面积计算等知识点,能把求不规则图形的面积转化成求规则图形的面积是解此题的关键,注意:圆心角为,半径为的扇形的面积.
4.【答案】
【解析】解:连接,作于,
点是直径为的半圆的中点,
,,
是等腰直角三角形,
分别以点和为圆心,以大于的长为半径作弧,且,
垂直平分,
,
,,
,
,
是的中位线,
,
,
,
,
.
故选:.
连接,作于,根据圆周角定理得到,,从而得到是等腰直角三角形,判断是的垂直平分线,进一步即可求得,求得,,得到,即可得到.
本题考查扇形的面积公式、圆周角定理,等腰直角三角形的判定和性质,线段垂直平分线的判定,解题的关键是解得,属于中考常考题型.
5.【答案】
【解析】解:连接,如图,
,
,,
,
,
,
,
,
的长.
故选:.
连接,如图,利用等腰三角形的性质和平行线的性质可计算出,然后根据弧长公式计算的长.
本题考查了弧长公式,等腰三角形的性质,平行线的性质等知识,熟练掌握基本图形的性质是解题的关键.
6.【答案】
【解析】解:将正方形绕点按逆时针方向旋转至正方形,
,
线段扫过的面积,
故选:.
根据中心对称的性质得到,根据扇形的面积公式即可得到结论.
本题考查了扇形的面积的计算,正方形的性质,熟练掌握扇形的面积公式是解题的关键.
7.【答案】
【解析】【分析】
本题主要考查了平行线的性质,圆周角定理,圆心角、弧、弦之间的关系,扇形面积的计算,弧长的计算,解答本题的关键是掌握利用“割补法”求面积的思路与方法;连接、,根据,得出,进一步得出,,,进而得出,利用弧长公式求出的度数为,进而得,再利用扇形面积公式进行解答,即可求解.
【解答】
解:连接、,如图:
,
,
,,
,
,
的长度为,设的度数为,
,
,
的度数为,
,
.
故选:.
8.【答案】
【解析】解:连接,,
为的直径,
,
,
,
即点是的中点,
点是的中点,
是的中位线,
,
,
,
,
,
,
,
,
,
,
故选:.
根据直径所对的圆周角是直角得到,再根据等腰三角形三线合一得出点是的中点,从而得出是的中位线,于是,根据同底等高得到和的面积相等,从而阴影部分的面积转化为扇形的面积,根据扇形面积公式计算出扇形的面积即可得出阴影部分的面积.
本题主要考查了扇形的面积,圆周角定理,中位线定理,平行线间的距离相等,等腰三角形的三线合一,不规则图形的面积求法,把不规则图形转化为规则图形计算面积是解题的关键.
9.【答案】
【解析】解:如图,设交于点,连接.
,,
,
,
,,
.
故选:.
设交于点,连接首先证明,根据求解即可.
本题考查扇形的面积,解直角三角形等知识,解题的关键是学会割补法求阴影部分的面积.
10.【答案】
【解析】解:如图所示:
,
,,
在中,
,,
,
,
解得:,
,
,
,
的长.
故选:.
先根据垂径定理求出的长,由题意得,在中利用勾股定理即可求出的值,然后再利用三角函数计算出所对的圆心角的度数,由弧长公式求出的长即可.
本题考查的是垂径定理,勾股定理及弧长的计算公式,根据垂径定理得出的长,再由勾股定理求出半径是解答此题的关键,同时要熟记圆弧长度的计算公式.
11.【答案】
【解析】【分析】
根据折叠的性质推出,,推出四边形是菱形,连接交于,根据等边三角形的性质得到,求得,根据菱形和扇形的面积公式即可得出答案.
本题考查了扇形面积的计算,菱形的判定和性质,等边三角形的判定和性质,正确地作出辅助线是解题的关键.
【解答】
解:沿折叠扇形纸片,点恰好落在上的点处,
,,
,
四边形是菱形,
连接交于,
,
是等边三角形,
,
,
,
,,
,
图中阴影部分的面积,
故选:.
12.【答案】
【解析】解:,,
,
,
,
,
的长度,
直接利用等腰三角形的性质得出的度数,再利用圆周角定理得出的度数,再利用弧长公式求出答案.
此题主要考查了弧长公式应用以及圆周角定理,正确得出的度数是解题关键.
13.【答案】
【解析】略
14.【答案】
【解析】解:由题意得,重物上升的距离是半径为,圆心角为所对应的弧长.
即:
故答案为:.
根据弧长的计算方法,计算弧长即可.
本题考查弧长的计算,熟练掌握弧长计算公式是关键.
15.【答案】
【解析】解:四边形是正方形,
,,,,
≌,
正方形的边长为,
,
阴影部分的面积为扇形的面积,即,
故答案为:.
根据正方形的性质得出阴影部分的面积为扇形的面积,然后由勾股定理得出,再由扇形面积公式求解即可.
本题主要考查正方形的性质以及扇形的面积,能够理解题意,将阴影部分的面积转化为扇形的面积是解题的关键.
16.【答案】
【解析】【分析】
本题考查的是正六边形的性质和弧长的计算、等腰三角形的性质、含度角的直角三角形的性质,勾股定理,掌握扇形弧长公式是解题的关键.
由正六边形的边长为,可得,,进而求出,,过作于,由等腰三角形的性质和含直角三角形的性质得到,,在中,由勾股定理求得,得到,根据扇形的弧长公式即可得到结论.
【解答】
解:正六边形的边长为,
,,
,
,
过作于,
,,
在中,,
,
同理可证,,
,
长度为
故答案为:
17.【答案】【小题】
证明:是的直径,.,,即,.
【小题】
,,,,的长为.
【解析】 见答案
见答案
18.【答案】解:联结,如图:
的直径,
,
的半径为,
,
,
,
∽,
,
,
,
关于的函数解析式为,定义域为
作,垂足为,如图:
是的弦,,
,
设两圆的公共弦与相交于,则垂直平分,
,
在中,,,
在中,,,
,
当点在线段上时,,
,
,
;
当点在线段上时,,
,
,
;
综上所述,公共弦的长为或;
能为等腰三角形,的长度为或.
【解析】【分析】
本题主要考查了圆的综合,圆的相关概念,相似三角形的判定与性质,函数关系式,自变量的取值范围,勾股定理,弧长的计算,解答本题的关键是掌握圆的相关概念与性质.
联结,证明∽,利用相似三角形的性质得出,即,进而得出关于的函数解析式,并写出定义域即可;
作,垂足为,根据垂径定理得出,设两圆的公共弦与相交于,则垂直平分,,根据锐角三角函数的概念得出,根据点的位置分两种情况:当点在线段上时,当点在线段上时,分情况画出图形,结合图形,求出的长,即可求解;
能为等腰三角形,分两种情况:当点在线段上时,,连接,当点在线段上时,,连接,分情况画出图形,结合图形,根据等腰三角形的性质,三角形的内角和定理求出的度数,再利用弧长公式进行解答,即可求解.
【解答】
解:见答案;
见答案;
能为等腰三角形,分两种情况:
当点在线段上时,,连接,如图:
则,
设,则,
,
,
,
,
,
,
,
,
,解得,
,
的长度为;
当点在线段上时,,连接,如图:
则,
设,则,
,
,
,
,
,
,
,
根据对顶角的性质可得,,
,
,解得,
,
的长度为;
综上所述,的长度为或.
19.【答案】解:把点代入,得.
反比例函数的解析式是.
矩形中,
,,.
.
由勾股定理得,
故CD.
由勾股定理得.
,
是等边三角形.
;
.
【解析】本题主要考查了待定系数法求反比例函数解析式,反比例函数的性质,勾股定理,扇形的面积等知识.
利用待定系数法求解即可;
由点的坐标确定出各线段的长,利用勾股定理求得,的长,证明是等边三角形,即可得解;
利用梯形的面积减去扇形的面积即可.
【解答】
解:见答案;
见答案;
阴影部分的面积梯形的面积扇形的面积
.
20.【答案】解:如图所示:即为所求,
,
旋转过程中点经过的路线长为:
【解析】此题主要考查了旋转变换以及弧长公式,勾股定理有关知识,直接利用旋转的性质得出对应点位置,再利用弧长公式得出答案
21.【答案】解:连接,
,过圆心,
,
,
,
;
,
,
,,过圆心,
,
则,
劣弧的长为
【解析】连接,根据垂径定理求出,根据圆周角定理求出,再求出答案即可;
求出圆心角的度数,解直角三角形求出,再根据弧长公式求出答案即可.
本题考查了垂径定理,圆周角定理,弧长公式,解直角三角形等知识点,能熟记垂径定理是解此题的关键.
22.【答案】解:如图所示,即为所求;
如图所示,即为所求;
将绕着原点顺时针旋转,得到,如图,连接交于,连接交于,
,,,
,,,
,
由旋转得:,,,,,
≌,
,
线段在旋转过程中扫过的面积.
【解析】根据平移的性质得出对应点的位置,画出平移后的图形即可;
利用轴对称的性质得出对应点的位置,画出图形即可;
根据题意画出旋转后的图形,先求得:,,,再利用线段在旋转过程中扫过的面积,即可求得答案.
本题考查简单作图、扇形面积的计算、平移变换、轴对称变换、旋转变换,解答本题的关键是明确题意,利用数形结合的思想解答.
23.【答案】
解:连接并延长,交交于点,连接,
是的直径,
.
在中,
,
,
,
,
又,
,
即与的长度之和为
【解析】【分析】
本题考查的是勾股定理,弧长的计算有关知识
根据所给三个问题,发现都用到了整体思想,据此可解决问题.
按要求继续表示出,再将转化为即可解决问题.
连接并延长,与交于点,利用勾股定理求出的值,发现,进一步得出即可解决问题.
【解答】
解:由题中所给三个问题可知,
在解决问题的过程中都用到了整体思想
继续问题的解题过程,
,
所以,
因为,
所以,
所以
见答案
24.【答案】解:等腰直角三角形;
如图,即为所求.
如图,即为所求,
扫过的面积为.
【解析】【分析】
本题主要考查作图轴对称变换和旋转变换,解题的关键是掌握轴对称变换与旋转变换的定义及其性质,扇形的面积公式等知识点.
根据勾股定理及其逆定理即可判断;
分别作出三顶点关于轴的对称点,再顺次连接可得答案;
作出点,绕点顺时针旋转的对应点,再顺次连接可得,旋转过程中三角形扫过的面积是三角形面积与扇形的面积和,据此列式计算.
【解答】
解:,,,
,且,
是等腰直角三角形,
故答案为:等腰直角三角形;
见答案;
见答案.
25.【答案】解:如图所示;
如图所示;
由网格图可知:,
根据旋转,,可知
根据旋转,,可知
由图可见:在旋转过程中扫过的面积为:
【解析】本题考查网格作图平移、旋转,以及网格中图形面积的计算,解题涉及平移的性质,旋转的性质,勾股定理,扇形面积公式,掌握平移、旋转的性质和网格中图形面积的计算方法是解题的关键.
按平移变换的性质分别确定,,平移后的位置,再按原来的连接方式连接即可;
按旋转变换的性质分别确定,,绕点顺时针旋转度后的位置,再按原来的连接方式连接即可;
在旋转过程中扫过的面积为:,根据扇形的面积公式求解即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.8弧长及扇形面积浙教版初中数学九年级上册同步练习
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.用一个圆心角为,半径为的扇形作一个圆锥的侧面,则这个圆锥的底面直径是( )
A. B. C. D.
2.一个滑轮起重装置如图所示,滑轮的半径是,当重物上升时,滑轮的一条半径绕轴心按顺时针方向旋转的角度约为 取,结果精确到
A. B. C. D.
3.如图,在扇形中,,半径,将扇形沿过点的直线折叠,点恰好落在上的点处,折痕交于点,则阴影部分的面积为( )
A. B. C. D.
4.如图,点是直径为的半圆的中点,连接,分别以点和为圆心,以大于的长为半径作弧,两弧相交于点,作直线交于点,连接,则阴影部分的面积为( )
A. B. C. D.
5.如图,在扇形中,,,若弦,则的长为( )
A.
B.
C.
D.
6.如图,在正方形中,边长,将正方形绕点按逆时针方向旋转至正方形,则线段扫过的面积为( )
A.
B.
C.
D.
7.如图,是半径为的半圆上的两个点,是直径,,若的长度为,则图中阴影部分的面积为
A. B. C. D.
8.如图,在中,,以为直径的与,分别交于点,,连接,,若,,则阴影部分的面积为( )
A. B. C. D.
9.如图,将扇形沿方向平移,使点移到的中点处,得到扇形若,,则阴影部分的面积为( )
A. B. C. D.
10.如图,一条公路的转弯处是一段圆弧,点是这段弧所在圆的圆心,为上一点,于若,,则的长为( )
A. B. C. D.
11.如图,扇形纸片的半径为,沿折叠扇形纸片,点恰好落在上的点处,图中阴影部分的面积为( )
A. B. C. D.
12.如图,为圆的直径,点在圆上,若,,则的长为
A. B. C. D.
二、填空题:本题共4小题,每小题3分,共12分。
13.如图,在中,,,则图中阴影部分的面积为 .
14.墨经是中国古籍中最早讨论滑轮力学的著作,如图所示是书中记载的一个滑轮机械,称为“绳制”,若图中的定滑轮半径为,滑轮旋转了,则重物“甲”上升了______绳索粗细不计,且与滑轮之间无滑动,结果保留
15.如图,正方形的边长为,对角线,相交于点,以点为圆心,对角线的长为半径画弧,交的延长线于点,则图中阴影部分的面积为______.
16.如图,正六边形的边长为,以为圆心,的长为半径画弧,得,则的长度为 .
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
如图,已知是的直径,,是上的点,,交于点,连结.
求证:.
若,,求的长.
18.本小题分
已知:的直径,与相交于点、,的直径与相交于点,设的半径为,的长为,
如图,当点在线段上时,求关于的函数解析式,并写出定义域;
当点在直径上时,如果的长为,求公共弦的长;
设与相交于,试问能否为等腰三角形?如果能够,请直接写出的长度不必写过程;如果不能,请简要说明理由.
19.本小题分
如图所示,矩形的边在轴上,在轴上,点的坐标是,反比例函数的图象经过点,以点为圆心,为半径作交边于点,连接.
求反比例函数的解析式.
求的度数.
请直接写出图中阴影部分的面积.
20.本小题分
如图,的顶点坐标分别为,,画出将绕点旋转后的,并求旋转过程中点经过的路线长.
21.本小题分
如图,在中,弦垂直于半径,垂足为点点是优弧上一点,连接,,,.
求的度数.
若,求图中劣弧的长.
22.本小题分
如图,在平面直角坐标系中,已知的三个顶点坐标分别是,.
将向上平移个单位,再向右平移个单位,得到,请画出;
请画出关于轴对称的;
将绕着原点顺时针旋转,得到,求线段在旋转过程中扫过的面积结果保留.
23.本小题分
学习下面方框内的内容,并解答下列问题:
小明在反思学习时,发现解决下列个问题时都用到了同一种数学思想方法:
问题若,求的值.
解决思路:.
问题如图,分别以的个顶点为圆心,为半径画圆,求图中块阴影面积之和.
解决思路:将块阴影扇形拼成一个半径为的半圆,则阴影面积为.
问题已知,求的值.
解题思路:对已知条件进行恒等变形,,,因为,所以,类似可以得到.
问题:
方框内个问题的解决都用到了 的数学思想方法从下列选项中选一个
A.分类讨论
B.数形结合
C.整体
D.从特殊到一般
方框内问题中的值为
如图,已知的半径为,、是的弦,且,,求与的长度之和.
24.本小题分
如图,平面直角坐标系中,的顶点都在正方形每个小正方形边长为单位网格的格点上.
的形状是______直接写答案
画出沿轴翻折后的;
画出绕点顺时针旋转的并求出旋转过程中扫过的面积.结果保留
25.本小题分
如图,网格中每个小正方形的边长均为个单位长度,的顶点均在小正方形的格点上.
将向下平移个单位长度得到,画出;
将绕点按顺时针方向旋转得到,画出;
在的条件下,请求出线段在旋转过程中扫过的面积.
答案和解析
1.【答案】
【解析】【分析】
本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.根据弧长公式先计算出扇形的弧长,再利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长求解.
【解答】
解:扇形的弧长,
设圆锥的底面直径为,则,
所以.
2.【答案】
【解析】【分析】
本题考查了弧长的计算公式:,其中表示弧长,表示弧所对的圆心角的度数.
重物上升,说明点转过的路径长为,然后根据弧长公式得到的方程,解方程即可.
【解答】
解:根据题意得,,
解得,,
所以绕轴心按逆时针方向旋转的角度约为.
故选:.
3.【答案】
【解析】解:连接,交于,
沿对折和重合,,
,,,,
,是等边三角形,
,
,
,
,
,
阴影部分的面积
,
故选:.
连接,交于,根据对折得出,,,,得出是等边三角形,根据等边三角形的性质得出,求出,求出,再分别求出扇形和的面积即可.
本题考查了等边三角形的性质和判定,直角三角形的性质,扇形的面积计算等知识点,能把求不规则图形的面积转化成求规则图形的面积是解此题的关键,注意:圆心角为,半径为的扇形的面积.
4.【答案】
【解析】解:连接,作于,
点是直径为的半圆的中点,
,,
是等腰直角三角形,
分别以点和为圆心,以大于的长为半径作弧,且,
垂直平分,
,
,,
,
,
是的中位线,
,
,
,
,
.
故选:.
连接,作于,根据圆周角定理得到,,从而得到是等腰直角三角形,判断是的垂直平分线,进一步即可求得,求得,,得到,即可得到.
本题考查扇形的面积公式、圆周角定理,等腰直角三角形的判定和性质,线段垂直平分线的判定,解题的关键是解得,属于中考常考题型.
5.【答案】
【解析】解:连接,如图,
,
,,
,
,
,
,
,
的长.
故选:.
连接,如图,利用等腰三角形的性质和平行线的性质可计算出,然后根据弧长公式计算的长.
本题考查了弧长公式,等腰三角形的性质,平行线的性质等知识,熟练掌握基本图形的性质是解题的关键.
6.【答案】
【解析】解:将正方形绕点按逆时针方向旋转至正方形,
,
线段扫过的面积,
故选:.
根据中心对称的性质得到,根据扇形的面积公式即可得到结论.
本题考查了扇形的面积的计算,正方形的性质,熟练掌握扇形的面积公式是解题的关键.
7.【答案】
【解析】【分析】
本题主要考查了平行线的性质,圆周角定理,圆心角、弧、弦之间的关系,扇形面积的计算,弧长的计算,解答本题的关键是掌握利用“割补法”求面积的思路与方法;连接、,根据,得出,进一步得出,,,进而得出,利用弧长公式求出的度数为,进而得,再利用扇形面积公式进行解答,即可求解.
【解答】
解:连接、,如图:
,
,
,,
,
,
的长度为,设的度数为,
,
,
的度数为,
,
.
故选:.
8.【答案】
【解析】解:连接,,
为的直径,
,
,
,
即点是的中点,
点是的中点,
是的中位线,
,
,
,
,
,
,
,
,
,
,
故选:.
根据直径所对的圆周角是直角得到,再根据等腰三角形三线合一得出点是的中点,从而得出是的中位线,于是,根据同底等高得到和的面积相等,从而阴影部分的面积转化为扇形的面积,根据扇形面积公式计算出扇形的面积即可得出阴影部分的面积.
本题主要考查了扇形的面积,圆周角定理,中位线定理,平行线间的距离相等,等腰三角形的三线合一,不规则图形的面积求法,把不规则图形转化为规则图形计算面积是解题的关键.
9.【答案】
【解析】解:如图,设交于点,连接.
,,
,
,
,,
.
故选:.
设交于点,连接首先证明,根据求解即可.
本题考查扇形的面积,解直角三角形等知识,解题的关键是学会割补法求阴影部分的面积.
10.【答案】
【解析】解:如图所示:
,
,,
在中,
,,
,
,
解得:,
,
,
,
的长.
故选:.
先根据垂径定理求出的长,由题意得,在中利用勾股定理即可求出的值,然后再利用三角函数计算出所对的圆心角的度数,由弧长公式求出的长即可.
本题考查的是垂径定理,勾股定理及弧长的计算公式,根据垂径定理得出的长,再由勾股定理求出半径是解答此题的关键,同时要熟记圆弧长度的计算公式.
11.【答案】
【解析】【分析】
根据折叠的性质推出,,推出四边形是菱形,连接交于,根据等边三角形的性质得到,求得,根据菱形和扇形的面积公式即可得出答案.
本题考查了扇形面积的计算,菱形的判定和性质,等边三角形的判定和性质,正确地作出辅助线是解题的关键.
【解答】
解:沿折叠扇形纸片,点恰好落在上的点处,
,,
,
四边形是菱形,
连接交于,
,
是等边三角形,
,
,
,
,,
,
图中阴影部分的面积,
故选:.
12.【答案】
【解析】解:,,
,
,
,
,
的长度,
直接利用等腰三角形的性质得出的度数,再利用圆周角定理得出的度数,再利用弧长公式求出答案.
此题主要考查了弧长公式应用以及圆周角定理,正确得出的度数是解题关键.
13.【答案】
【解析】略
14.【答案】
【解析】解:由题意得,重物上升的距离是半径为,圆心角为所对应的弧长.
即:
故答案为:.
根据弧长的计算方法,计算弧长即可.
本题考查弧长的计算,熟练掌握弧长计算公式是关键.
15.【答案】
【解析】解:四边形是正方形,
,,,,
≌,
正方形的边长为,
,
阴影部分的面积为扇形的面积,即,
故答案为:.
根据正方形的性质得出阴影部分的面积为扇形的面积,然后由勾股定理得出,再由扇形面积公式求解即可.
本题主要考查正方形的性质以及扇形的面积,能够理解题意,将阴影部分的面积转化为扇形的面积是解题的关键.
16.【答案】
【解析】【分析】
本题考查的是正六边形的性质和弧长的计算、等腰三角形的性质、含度角的直角三角形的性质,勾股定理,掌握扇形弧长公式是解题的关键.
由正六边形的边长为,可得,,进而求出,,过作于,由等腰三角形的性质和含直角三角形的性质得到,,在中,由勾股定理求得,得到,根据扇形的弧长公式即可得到结论.
【解答】
解:正六边形的边长为,
,,
,
,
过作于,
,,
在中,,
,
同理可证,,
,
长度为
故答案为:
17.【答案】【小题】
证明:是的直径,.,,即,.
【小题】
,,,,的长为.
【解析】 见答案
见答案
18.【答案】解:联结,如图:
的直径,
,
的半径为,
,
,
,
∽,
,
,
,
关于的函数解析式为,定义域为
作,垂足为,如图:
是的弦,,
,
设两圆的公共弦与相交于,则垂直平分,
,
在中,,,
在中,,,
,
当点在线段上时,,
,
,
;
当点在线段上时,,
,
,
;
综上所述,公共弦的长为或;
能为等腰三角形,的长度为或.
【解析】【分析】
本题主要考查了圆的综合,圆的相关概念,相似三角形的判定与性质,函数关系式,自变量的取值范围,勾股定理,弧长的计算,解答本题的关键是掌握圆的相关概念与性质.
联结,证明∽,利用相似三角形的性质得出,即,进而得出关于的函数解析式,并写出定义域即可;
作,垂足为,根据垂径定理得出,设两圆的公共弦与相交于,则垂直平分,,根据锐角三角函数的概念得出,根据点的位置分两种情况:当点在线段上时,当点在线段上时,分情况画出图形,结合图形,求出的长,即可求解;
能为等腰三角形,分两种情况:当点在线段上时,,连接,当点在线段上时,,连接,分情况画出图形,结合图形,根据等腰三角形的性质,三角形的内角和定理求出的度数,再利用弧长公式进行解答,即可求解.
【解答】
解:见答案;
见答案;
能为等腰三角形,分两种情况:
当点在线段上时,,连接,如图:
则,
设,则,
,
,
,
,
,
,
,
,
,解得,
,
的长度为;
当点在线段上时,,连接,如图:
则,
设,则,
,
,
,
,
,
,
,
根据对顶角的性质可得,,
,
,解得,
,
的长度为;
综上所述,的长度为或.
19.【答案】解:把点代入,得.
反比例函数的解析式是.
矩形中,
,,.
.
由勾股定理得,
故CD.
由勾股定理得.
,
是等边三角形.
;
.
【解析】本题主要考查了待定系数法求反比例函数解析式,反比例函数的性质,勾股定理,扇形的面积等知识.
利用待定系数法求解即可;
由点的坐标确定出各线段的长,利用勾股定理求得,的长,证明是等边三角形,即可得解;
利用梯形的面积减去扇形的面积即可.
【解答】
解:见答案;
见答案;
阴影部分的面积梯形的面积扇形的面积
.
20.【答案】解:如图所示:即为所求,
,
旋转过程中点经过的路线长为:
【解析】此题主要考查了旋转变换以及弧长公式,勾股定理有关知识,直接利用旋转的性质得出对应点位置,再利用弧长公式得出答案
21.【答案】解:连接,
,过圆心,
,
,
,
;
,
,
,,过圆心,
,
则,
劣弧的长为
【解析】连接,根据垂径定理求出,根据圆周角定理求出,再求出答案即可;
求出圆心角的度数,解直角三角形求出,再根据弧长公式求出答案即可.
本题考查了垂径定理,圆周角定理,弧长公式,解直角三角形等知识点,能熟记垂径定理是解此题的关键.
22.【答案】解:如图所示,即为所求;
如图所示,即为所求;
将绕着原点顺时针旋转,得到,如图,连接交于,连接交于,
,,,
,,,
,
由旋转得:,,,,,
≌,
,
线段在旋转过程中扫过的面积.
【解析】根据平移的性质得出对应点的位置,画出平移后的图形即可;
利用轴对称的性质得出对应点的位置,画出图形即可;
根据题意画出旋转后的图形,先求得:,,,再利用线段在旋转过程中扫过的面积,即可求得答案.
本题考查简单作图、扇形面积的计算、平移变换、轴对称变换、旋转变换,解答本题的关键是明确题意,利用数形结合的思想解答.
23.【答案】
解:连接并延长,交交于点,连接,
是的直径,
.
在中,
,
,
,
,
又,
,
即与的长度之和为
【解析】【分析】
本题考查的是勾股定理,弧长的计算有关知识
根据所给三个问题,发现都用到了整体思想,据此可解决问题.
按要求继续表示出,再将转化为即可解决问题.
连接并延长,与交于点,利用勾股定理求出的值,发现,进一步得出即可解决问题.
【解答】
解:由题中所给三个问题可知,
在解决问题的过程中都用到了整体思想
继续问题的解题过程,
,
所以,
因为,
所以,
所以
见答案
24.【答案】解:等腰直角三角形;
如图,即为所求.
如图,即为所求,
扫过的面积为.
【解析】【分析】
本题主要考查作图轴对称变换和旋转变换,解题的关键是掌握轴对称变换与旋转变换的定义及其性质,扇形的面积公式等知识点.
根据勾股定理及其逆定理即可判断;
分别作出三顶点关于轴的对称点,再顺次连接可得答案;
作出点,绕点顺时针旋转的对应点,再顺次连接可得,旋转过程中三角形扫过的面积是三角形面积与扇形的面积和,据此列式计算.
【解答】
解:,,,
,且,
是等腰直角三角形,
故答案为:等腰直角三角形;
见答案;
见答案.
25.【答案】解:如图所示;
如图所示;
由网格图可知:,
根据旋转,,可知
根据旋转,,可知
由图可见:在旋转过程中扫过的面积为:
【解析】本题考查网格作图平移、旋转,以及网格中图形面积的计算,解题涉及平移的性质,旋转的性质,勾股定理,扇形面积公式,掌握平移、旋转的性质和网格中图形面积的计算方法是解题的关键.
按平移变换的性质分别确定,,平移后的位置,再按原来的连接方式连接即可;
按旋转变换的性质分别确定,,绕点顺时针旋转度后的位置,再按原来的连接方式连接即可;
在旋转过程中扫过的面积为:,根据扇形的面积公式求解即可.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
