浙教版八年级数学下册课件:第6章 反比例函数复习课课件(共33张PPT)
文档属性
| 名称 | 浙教版八年级数学下册课件:第6章 反比例函数复习课课件(共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 208.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-20 18:42:51 | ||
图片预览





文档简介
课件33张PPT。第6章 反比例函数复习课(k≠0) y=kx-1(k≠0)xy = k (k≠0)一.反比例函数的表达形式 例1:
(1)y是关于x的反比例函数,当x=-3时,
y=0.6;求函数解析式和自变量x的取值范围。
(2)y与x+1成反比例,当x=2时,y=-1,
求函数解析式和自变量x的取值范围。
(3)已知y=y1+y2,y1与x-1成正比例,y2与x成反
比例,且当x=2时y=4;x=3时,y=6.求x=4时,y的值. 图象是双曲线 当k>0时, 双曲线分别位于第一,三象限内
当k<0时, 双曲线分别位于第二,四象限内 形 状位 置变化趋势双曲线无限接近于x、y轴,但永远不会与坐标轴相交
︱k︱越小,双曲线越靠近原点二、反比例函数图象及性质增 减 性
当k>0时,在每一个象限内, y随x的增大而减小
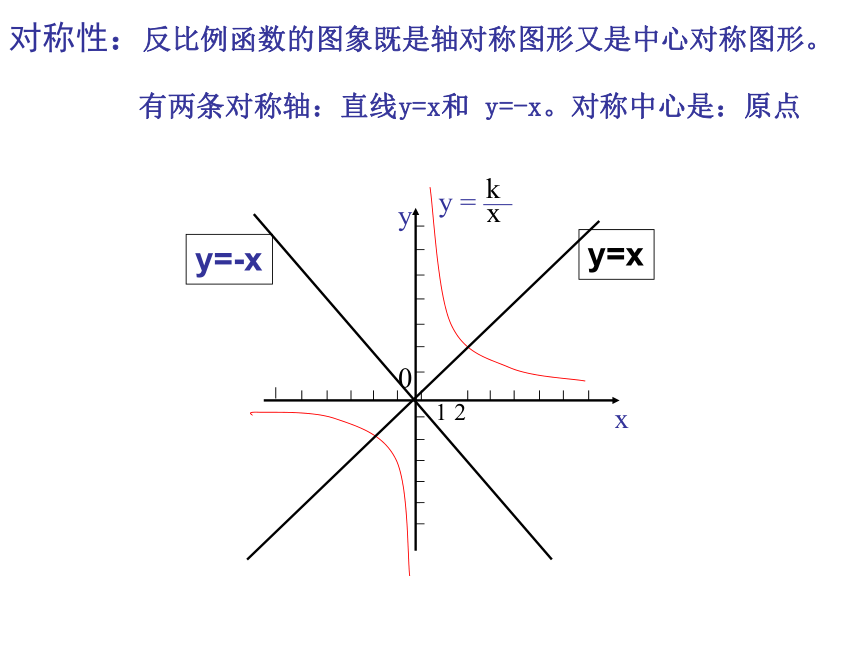
当k<0时,在每一个象限内,y随x的增大而增大对称性:反比例函数的图象既是轴对称图形又是中心对称图形。
有两条对称轴:直线y=x和 y=-x。对称中心是:原点xy012例2、已知反比例函数 的图象经过点A(1,4)(1 )①求此反比例函数 的解析式;
②画出图像;
③并判断点B(-4,-1)是否在此函数图像上。(2)根据图像得,
若y ﹥ 1, 则x的取值范围-----------
若x ﹤ 1,则y的取值范围-----------(3)若点(x1,y1), (x2,y2), (x3,y3),
均在此函数图像上,且x1 ﹤0﹤ x2 ﹤ x3
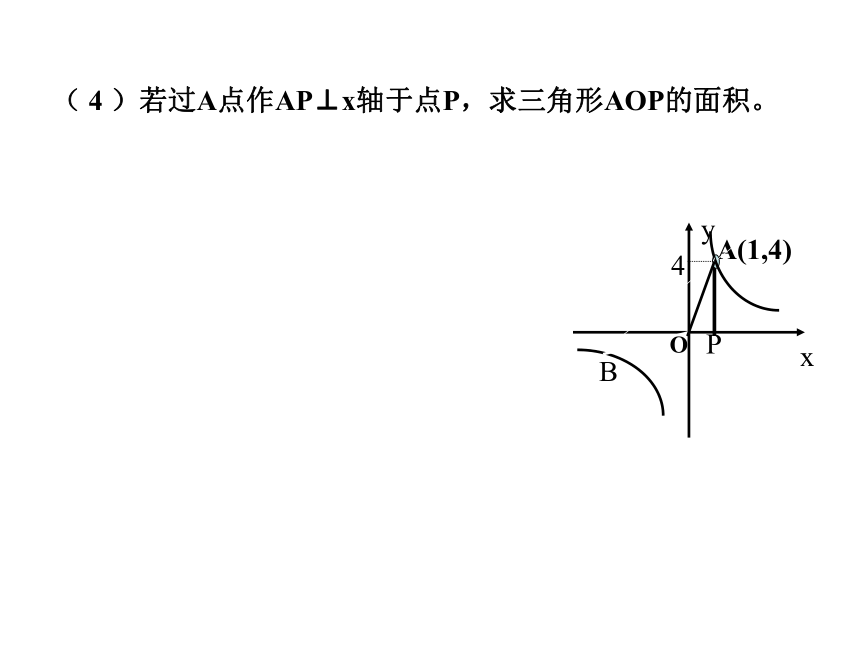
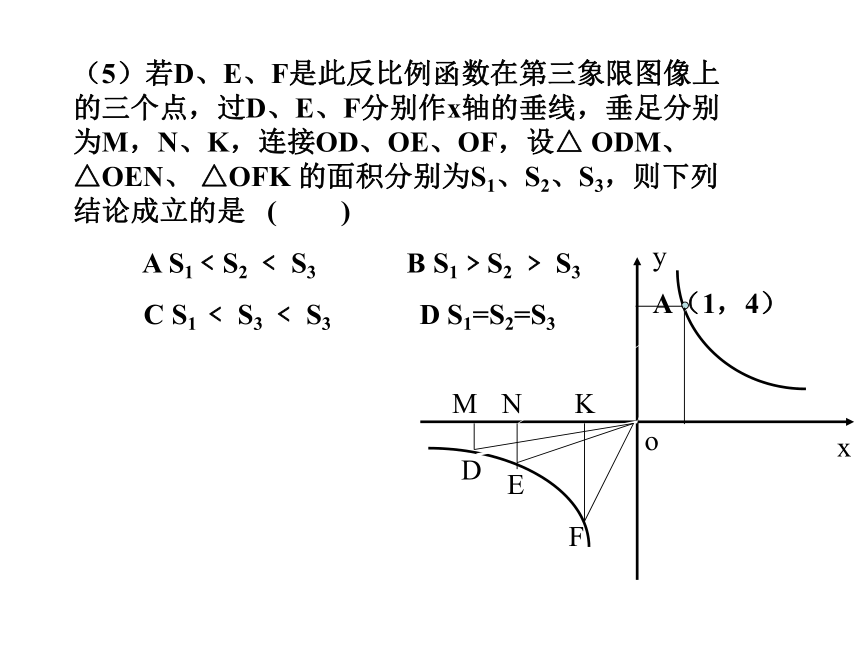
请比较y1、y2、y3的大小( 4 )若过A点作AP⊥x轴于点P,求三角形AOP的面积。(5)若D、E、F是此反比例函数在第三象限图像上的三个点,过D、E、F分别作x轴的垂线,垂足分别为M,N、K,连接OD、OE、OF,设△ ODM、△OEN、 △OFK 的面积分别为S1、S2、S3,则下列结论成立的是 ( ) A S1﹤S2 ﹤ S3 B S1﹥S2 ﹥ S3
C S1 ﹤ S3 ﹤ S3 D S1=S2=S3(7)连OA、OB,设点C是直线AB与y轴的交点,
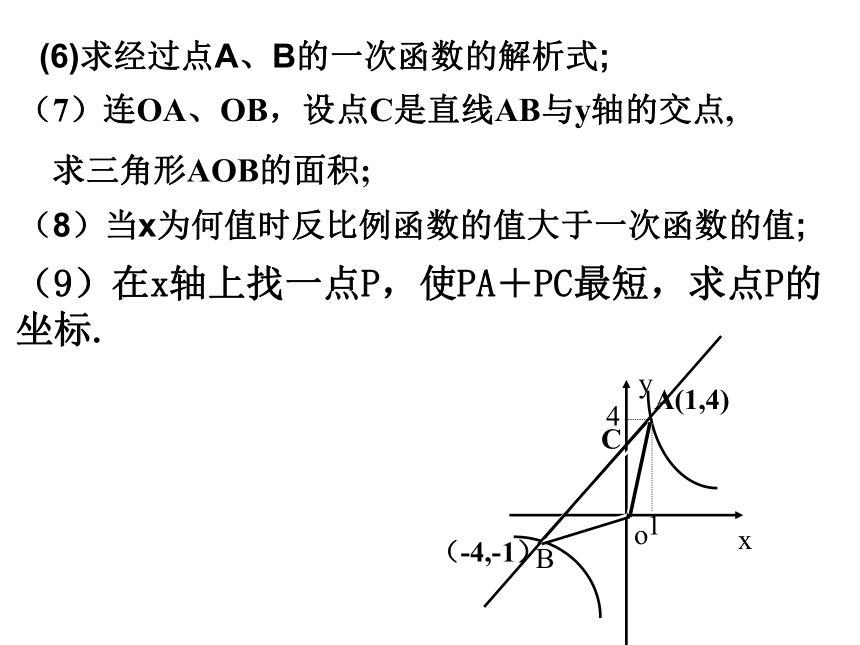
求三角形AOB的面积;(-4,-1)(8)当x为何值时反比例函数的值大于一次函数的值;(9)在x轴上找一点P,使PA+PC最短,求点P的坐标.(6)求经过点A、B的一次函数的解析式;C例3、已知反比例函数y =k/x 和一次函数 y=kx+b
的图象都经过点(2,1)
(1)分别求出这个函数的解析式
(2)试判断是A(-2, -1)在哪个函数的图象上
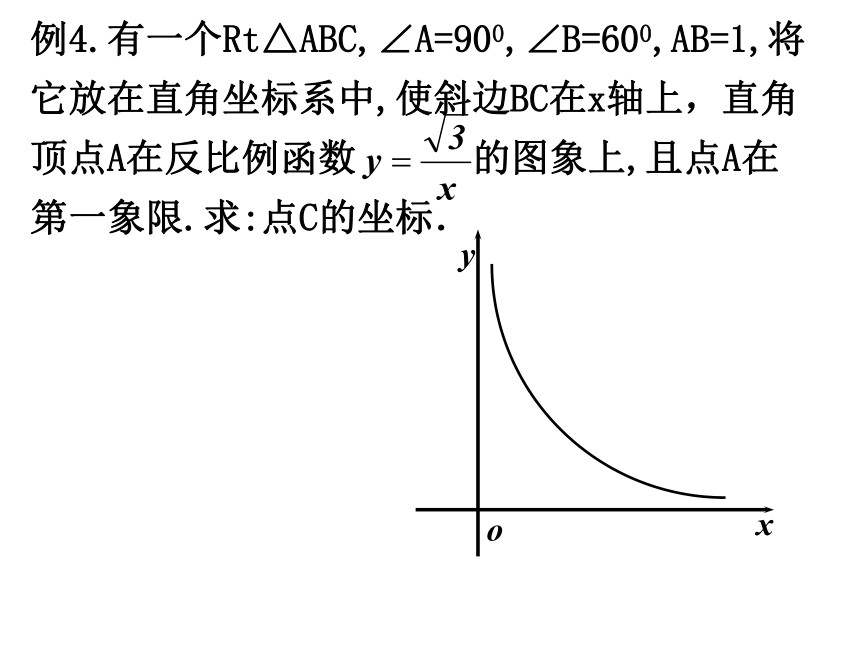
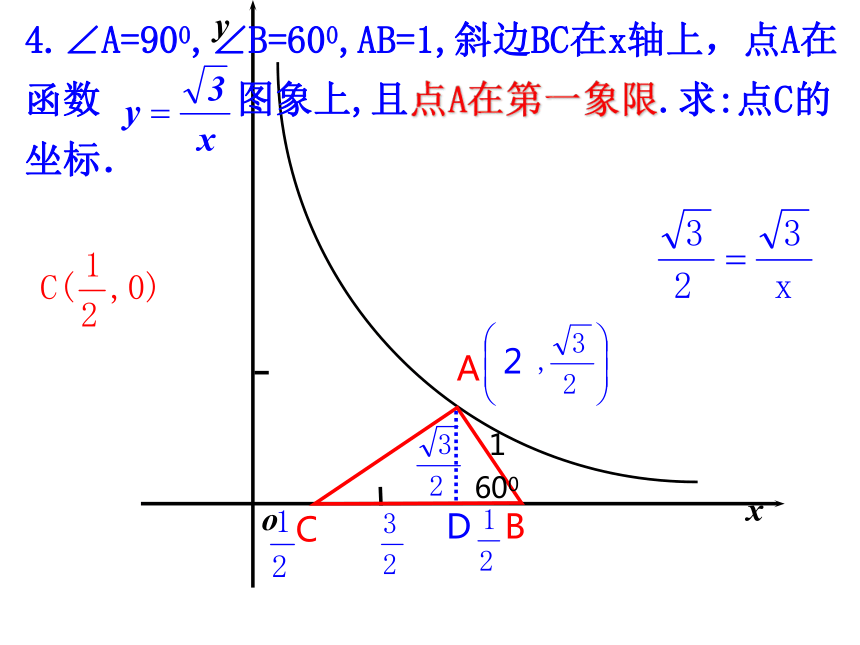
(3)求这两个函数的交点坐标例4.有一个Rt△ABC,∠A=900,∠B=600,AB=1,将它放在直角坐标系中,使斜边BC在x轴上,直角顶点A在反比例函数 的图象上,且点A在第一象限.求:点C的坐标. 4.∠A=900,∠B=600,AB=1,斜边BC在x轴上,点A在函数 图象上,且点A在第一象限.求:点C的坐标. 22A4.∠A=900,∠B=600,AB=1,斜边BC在x轴上,点A在函数 图象上.求:点C的坐标. o4.∠A=900,∠B=600,AB=1,斜边BC在坐标轴上,点A在函数 图象上.求:点C的坐标. C6今天你有什么收获 例2:老师家离我们学校大约50km, 设汽车从老师家开往我们学校的平均速度为V(km/h),开完全程用了t(h)(1) t关于v的函数关系式为 。 (2) t关于v的函数图象大致是( )(t>0)(3)、若汽车平均速度为40 (km/h).则开完全程用了多少小时?(4)、若规定汽车的平均速度不超过60 (km/h).为了尽快到达温州,且不超速,则至少需要多少时间?小组竞赛21341.函数 是 函数,其图象为 ,其中k= ,自变量x的取值范围为 .
2.函数 的图象位于第 象限,
在每一象限内,y的值随x的增大而 ,
当x>0时,y 0,这部分图象位于第 象限.反比例双曲线2x≠ 0一、三减小>一3、当反比例函数 y= 的图象满足y随x的增大而减小时,m的取值范围是 __________。m> -14.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .5.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .6.已知反比例函数 (k≠0)
当x<0时,y随x的增大而减小, ,则一次函数y=kx+k的图象不经过第 象限.k>0四3.已知函数y=k/x 的图象如下右图,则y=k x-2 的图象大致是( )xxxxxyyyyyooooo(A)(D)(C)(B)D6.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .y1 >0>y2y1>y2做一做1.如果反比例函数 的图象位于第二、四象限,那么m的范围为 .由1-3m<0
得-3m<- 1 m>做一做2.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .(m,n)1S△POD = OD·PD
=
==1想一想例1。如图,已知反比例函数 y= 的图象与一次函数
y= kx+4的图象相交于P、Q两点,且P点的纵坐标是6.
(1)求这个一次函数的解析式
(2)求△POQ的面积例2.在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其图象如图所示:
(1)求p与S之间的函数关系式;
(2)求当S=0.5m2时物体承受的压强p ;
(3)求当p=2500Pa时物体的受力面积S. 1.所受压力为F (F为常数且F≠ 0) 的物体,所受压强P与所受面积S的图象大致为( )PPPPSSSSOOOO(A)(B)(C)(D)B练一练PPPPFFFFOOOO(A)(B)(C)(D)2.受力面积为S (S为常数并且不为0)的物体所受
压强P与所受压力F的图象大致为( )A6.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .理一理在每一个象限内:
当k>0时,y随x的增大而减小;
当k<0时,y随x的增大而增大.y=kx(k≠0)( 特殊的一次函数)当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.
(1)y是关于x的反比例函数,当x=-3时,
y=0.6;求函数解析式和自变量x的取值范围。
(2)y与x+1成反比例,当x=2时,y=-1,
求函数解析式和自变量x的取值范围。
(3)已知y=y1+y2,y1与x-1成正比例,y2与x成反
比例,且当x=2时y=4;x=3时,y=6.求x=4时,y的值. 图象是双曲线 当k>0时, 双曲线分别位于第一,三象限内
当k<0时, 双曲线分别位于第二,四象限内 形 状位 置变化趋势双曲线无限接近于x、y轴,但永远不会与坐标轴相交
︱k︱越小,双曲线越靠近原点二、反比例函数图象及性质增 减 性
当k>0时,在每一个象限内, y随x的增大而减小
当k<0时,在每一个象限内,y随x的增大而增大对称性:反比例函数的图象既是轴对称图形又是中心对称图形。
有两条对称轴:直线y=x和 y=-x。对称中心是:原点xy012例2、已知反比例函数 的图象经过点A(1,4)(1 )①求此反比例函数 的解析式;
②画出图像;
③并判断点B(-4,-1)是否在此函数图像上。(2)根据图像得,
若y ﹥ 1, 则x的取值范围-----------
若x ﹤ 1,则y的取值范围-----------(3)若点(x1,y1), (x2,y2), (x3,y3),
均在此函数图像上,且x1 ﹤0﹤ x2 ﹤ x3
请比较y1、y2、y3的大小( 4 )若过A点作AP⊥x轴于点P,求三角形AOP的面积。(5)若D、E、F是此反比例函数在第三象限图像上的三个点,过D、E、F分别作x轴的垂线,垂足分别为M,N、K,连接OD、OE、OF,设△ ODM、△OEN、 △OFK 的面积分别为S1、S2、S3,则下列结论成立的是 ( ) A S1﹤S2 ﹤ S3 B S1﹥S2 ﹥ S3
C S1 ﹤ S3 ﹤ S3 D S1=S2=S3(7)连OA、OB,设点C是直线AB与y轴的交点,
求三角形AOB的面积;(-4,-1)(8)当x为何值时反比例函数的值大于一次函数的值;(9)在x轴上找一点P,使PA+PC最短,求点P的坐标.(6)求经过点A、B的一次函数的解析式;C例3、已知反比例函数y =k/x 和一次函数 y=kx+b
的图象都经过点(2,1)
(1)分别求出这个函数的解析式
(2)试判断是A(-2, -1)在哪个函数的图象上
(3)求这两个函数的交点坐标例4.有一个Rt△ABC,∠A=900,∠B=600,AB=1,将它放在直角坐标系中,使斜边BC在x轴上,直角顶点A在反比例函数 的图象上,且点A在第一象限.求:点C的坐标. 4.∠A=900,∠B=600,AB=1,斜边BC在x轴上,点A在函数 图象上,且点A在第一象限.求:点C的坐标. 22A4.∠A=900,∠B=600,AB=1,斜边BC在x轴上,点A在函数 图象上.求:点C的坐标. o4.∠A=900,∠B=600,AB=1,斜边BC在坐标轴上,点A在函数 图象上.求:点C的坐标. C6今天你有什么收获 例2:老师家离我们学校大约50km, 设汽车从老师家开往我们学校的平均速度为V(km/h),开完全程用了t(h)(1) t关于v的函数关系式为 。 (2) t关于v的函数图象大致是( )(t>0)(3)、若汽车平均速度为40 (km/h).则开完全程用了多少小时?(4)、若规定汽车的平均速度不超过60 (km/h).为了尽快到达温州,且不超速,则至少需要多少时间?小组竞赛21341.函数 是 函数,其图象为 ,其中k= ,自变量x的取值范围为 .
2.函数 的图象位于第 象限,
在每一象限内,y的值随x的增大而 ,
当x>0时,y 0,这部分图象位于第 象限.反比例双曲线2x≠ 0一、三减小>一3、当反比例函数 y= 的图象满足y随x的增大而减小时,m的取值范围是 __________。m> -14.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .5.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .6.已知反比例函数 (k≠0)
当x<0时,y随x的增大而减小, ,则一次函数y=kx+k的图象不经过第 象限.k>0四3.已知函数y=k/x 的图象如下右图,则y=k x-2 的图象大致是( )xxxxxyyyyyooooo(A)(D)(C)(B)D6.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .y1 >0>y2y1>y2做一做1.如果反比例函数 的图象位于第二、四象限,那么m的范围为 .由1-3m<0
得-3m<- 1 m>做一做2.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .(m,n)1S△POD = OD·PD
=
==1想一想例1。如图,已知反比例函数 y= 的图象与一次函数
y= kx+4的图象相交于P、Q两点,且P点的纵坐标是6.
(1)求这个一次函数的解析式
(2)求△POQ的面积例2.在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(m2)的反比例函数,其图象如图所示:
(1)求p与S之间的函数关系式;
(2)求当S=0.5m2时物体承受的压强p ;
(3)求当p=2500Pa时物体的受力面积S. 1.所受压力为F (F为常数且F≠ 0) 的物体,所受压强P与所受面积S的图象大致为( )PPPPSSSSOOOO(A)(B)(C)(D)B练一练PPPPFFFFOOOO(A)(B)(C)(D)2.受力面积为S (S为常数并且不为0)的物体所受
压强P与所受压力F的图象大致为( )A6.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .理一理在每一个象限内:
当k>0时,y随x的增大而减小;
当k<0时,y随x的增大而增大.y=kx(k≠0)( 特殊的一次函数)当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
