1.5 三角形全等的判定 课件(共18张PPT)2024-2025学年浙教版数学八年级上册
文档属性
| 名称 | 1.5 三角形全等的判定 课件(共18张PPT)2024-2025学年浙教版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 20:29:39 | ||
图片预览



文档简介
(共18张PPT)
课本P25-28
钱塘江大桥(Qiantang River Bridge),又名钱江一桥,是中国浙江省杭州市境的一座跨钱塘江双层桁架梁桥,位于西湖之南,六和塔附近钱塘江上,由中国桥梁专家茅以升主持全部结构设计,是中国自行设计、建造的第一座双层铁路、公路两用桥。桥上有许多全等的三角形结构。
全等三角形的定义:能够重合的两个三角形叫做全等三角形。
全等三角形的性质:全等三角形对应角相等;对应边相等;
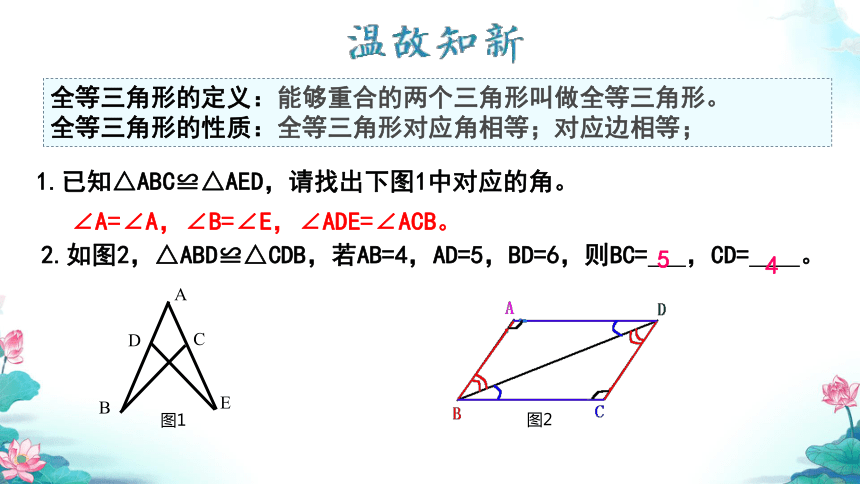
1.已知△ABC≌△AED,请找出下图1中对应的角。
∠A=∠A,∠B=∠E,∠ADE=∠ACB。
2.如图2,△ABD≌△CDB,若AB=4,AD=5,BD=6,则BC= ,CD= 。
5
4
A
B
C
D
E
图1
图2
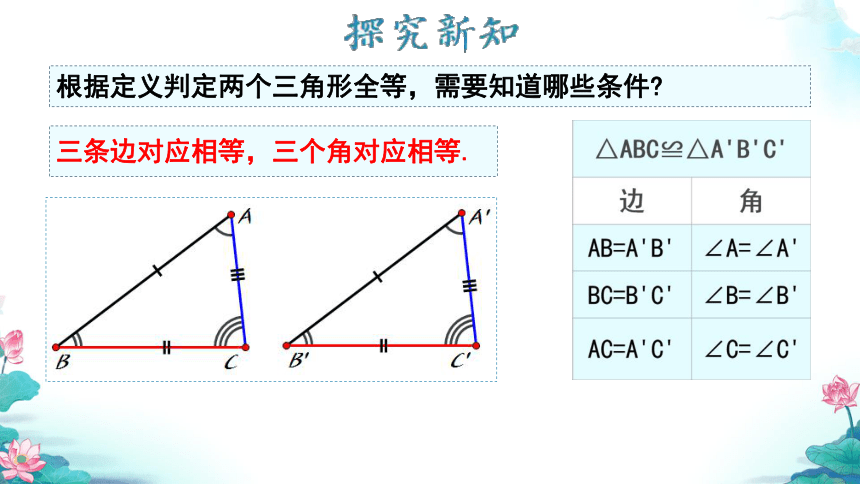
根据定义判定两个三角形全等,需要知道哪些条件
三条边对应相等,三个角对应相等.
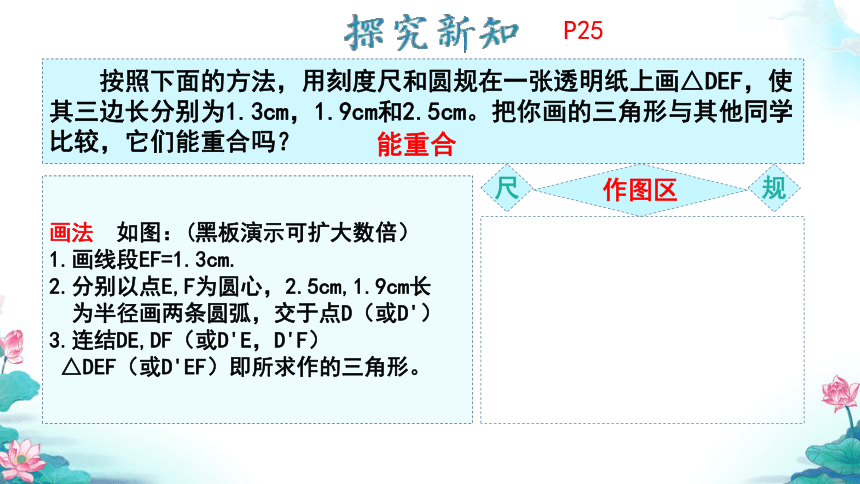
按照下面的方法,用刻度尺和圆规在一张透明纸上画△DEF,使其三边长分别为1.3cm,1.9cm和2.5cm。把你画的三角形与其他同学比较,它们能重合吗?
画法 如图:(黑板演示可扩大数倍)
1.画线段EF=1.3cm.
2.分别以点E,F为圆心,2.5cm,1.9cm长
为半径画两条圆弧,交于点D(或D')
3.连结DE,DF(或D'E,D'F)
△DEF(或D'EF)即所求作的三角形。
能重合
P25
UOTU
尺
规
作图区
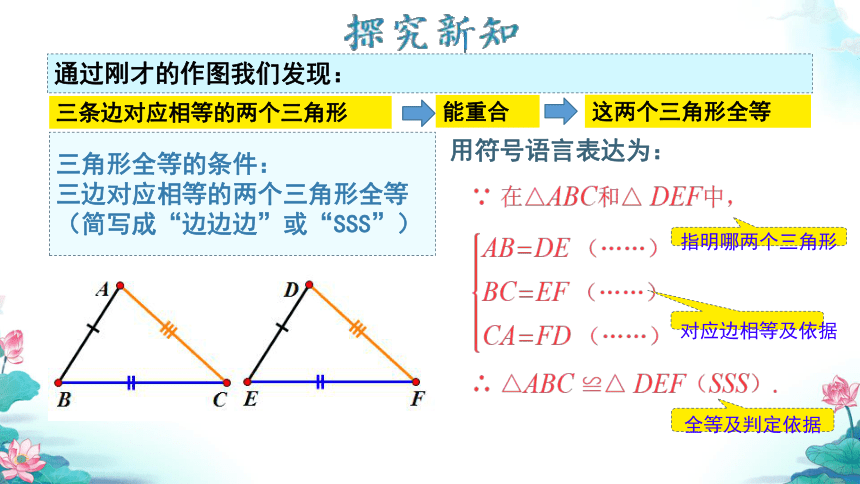
通过刚才的作图我们发现:
三角形全等的条件:
三边对应相等的两个三角形全等
(简写成“边边边”或“SSS”)
三条边对应相等的两个三角形
能重合
这两个三角形全等
用符号语言表达为:
指明哪两个三角形
对应边相等及依据
全等及判定依据
例1 已知:如图,在四边形ABCD中,AB=CD,AD=CB.
求证:∠A=∠C.
P26
P27
已知
DE
已知
已知
AC
EF
SSS
例2 已知∠BAC,用直尺和圆规作∠BAC的平分线AD,并说出该作法正确的理由.
作图区
尺
规
当三角形的三条边长确定时,三角形的形状、大小完全被确定。
三角形的稳定性
(三角形的特有性质)
思考
你能用SSS来解释三角形的稳定性吗?
因为只要给定了一个三角形的三条边,那么根据全等三角形的判定可知,当两个三角形三条边相等时,两个三角形全等,形状和大小不变,只是位置发生了变化,这样的三角形唯一确定. 故三角形具有稳定性.
1.如图,已知线段a,b,c.用直尺和圆规作△ABC,使BC=a,AC=B,AB=C.
作图区
尺
规
1.如图所示,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( )个.
4
2.如图,建筑工人砌墙,在加入门框时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法是利用( )
A.长方形的四个角都是直角 B.两点之间线段最短
C.长方形的对称性 D.三角形的稳定性
D
3.已知:点E,C在线段B上,BE=CF,AB=DE,AC=DF.
求证:△ABC≌△DEF.
证明:∵BE=CF,
∴BE+EC=CF+EC,即CB=EF;
∴△ABC≌△DEF(SSS)
1.三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)
注意几何语言规范
2.三角形具有稳定性。房屋的人字架、大桥的钢梁、起重机的支架、自行车的车座等,采用三角形结构,起到稳固的作用。
5.已知:如图,AB=DE,BC=EF,AF=DC.求证:BC∥EF.
提示:由已知可得△ABC≌△DEF(SSS),
∴ ∠EFD=∠BCA(全等三角形的对应角相等),
∴ ∠EFC=∠BCA(等角的补角相等),
∴ EF∥BC(内错角相等,两直线平行).
课本P25-28
钱塘江大桥(Qiantang River Bridge),又名钱江一桥,是中国浙江省杭州市境的一座跨钱塘江双层桁架梁桥,位于西湖之南,六和塔附近钱塘江上,由中国桥梁专家茅以升主持全部结构设计,是中国自行设计、建造的第一座双层铁路、公路两用桥。桥上有许多全等的三角形结构。
全等三角形的定义:能够重合的两个三角形叫做全等三角形。
全等三角形的性质:全等三角形对应角相等;对应边相等;
1.已知△ABC≌△AED,请找出下图1中对应的角。
∠A=∠A,∠B=∠E,∠ADE=∠ACB。
2.如图2,△ABD≌△CDB,若AB=4,AD=5,BD=6,则BC= ,CD= 。
5
4
A
B
C
D
E
图1
图2
根据定义判定两个三角形全等,需要知道哪些条件
三条边对应相等,三个角对应相等.
按照下面的方法,用刻度尺和圆规在一张透明纸上画△DEF,使其三边长分别为1.3cm,1.9cm和2.5cm。把你画的三角形与其他同学比较,它们能重合吗?
画法 如图:(黑板演示可扩大数倍)
1.画线段EF=1.3cm.
2.分别以点E,F为圆心,2.5cm,1.9cm长
为半径画两条圆弧,交于点D(或D')
3.连结DE,DF(或D'E,D'F)
△DEF(或D'EF)即所求作的三角形。
能重合
P25
UOTU
尺
规
作图区
通过刚才的作图我们发现:
三角形全等的条件:
三边对应相等的两个三角形全等
(简写成“边边边”或“SSS”)
三条边对应相等的两个三角形
能重合
这两个三角形全等
用符号语言表达为:
指明哪两个三角形
对应边相等及依据
全等及判定依据
例1 已知:如图,在四边形ABCD中,AB=CD,AD=CB.
求证:∠A=∠C.
P26
P27
已知
DE
已知
已知
AC
EF
SSS
例2 已知∠BAC,用直尺和圆规作∠BAC的平分线AD,并说出该作法正确的理由.
作图区
尺
规
当三角形的三条边长确定时,三角形的形状、大小完全被确定。
三角形的稳定性
(三角形的特有性质)
思考
你能用SSS来解释三角形的稳定性吗?
因为只要给定了一个三角形的三条边,那么根据全等三角形的判定可知,当两个三角形三条边相等时,两个三角形全等,形状和大小不变,只是位置发生了变化,这样的三角形唯一确定. 故三角形具有稳定性.
1.如图,已知线段a,b,c.用直尺和圆规作△ABC,使BC=a,AC=B,AB=C.
作图区
尺
规
1.如图所示,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出( )个.
4
2.如图,建筑工人砌墙,在加入门框时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法是利用( )
A.长方形的四个角都是直角 B.两点之间线段最短
C.长方形的对称性 D.三角形的稳定性
D
3.已知:点E,C在线段B上,BE=CF,AB=DE,AC=DF.
求证:△ABC≌△DEF.
证明:∵BE=CF,
∴BE+EC=CF+EC,即CB=EF;
∴△ABC≌△DEF(SSS)
1.三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)
注意几何语言规范
2.三角形具有稳定性。房屋的人字架、大桥的钢梁、起重机的支架、自行车的车座等,采用三角形结构,起到稳固的作用。
5.已知:如图,AB=DE,BC=EF,AF=DC.求证:BC∥EF.
提示:由已知可得△ABC≌△DEF(SSS),
∴ ∠EFD=∠BCA(全等三角形的对应角相等),
∴ ∠EFC=∠BCA(等角的补角相等),
∴ EF∥BC(内错角相等,两直线平行).
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
