1.6 尺规作图 课件(共22张PPT)2024-2025学年浙教版数学八年级上册
文档属性
| 名称 | 1.6 尺规作图 课件(共22张PPT)2024-2025学年浙教版数学八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 14.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 20:36:48 | ||
图片预览







文档简介
(共22张PPT)
P36-39
已知:线段a,求作一条线段等于a.
(3)在射线AC 上截取AB =a ,则线段 AB 就是所要画的线段.
(1)先画射线AC;
(2)用圆规量出线段a的长;
尺规作法:
尺
规
作图区
据传为了显示谁的逻辑思维能力更强,古希腊人限制了几何作图的工具,结果一些普通的画图题让数学家苦苦思索了两千多年.尺规作图特有的魅力,使无数人沉湎其中。
想一想:你知道什么是尺规作图吗?尺规的基本作用分别是什么?
只用没有刻度的直尺和圆规作图称为尺规作图.
尺规作图的工具只能是直尺和圆规,其中直尺用来作直线、线段、射线或延长线段等;圆规用来作圆或圆孤等.
值得注意的是直尺是没有刻度的或不考虑刻度的存在.
尺规作图是指用无刻度的直尺和圆规作图。尺规作图是起源于古希腊的数学课题。只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题。尺规作图使用的直尺和圆规带有想象性质,跟现实中的并非完全相同:
1、直尺必须没有刻度,无限长,且只能使用直尺的固定一侧。只可以用它来将两个点连在一起,不可以在上画刻度;
2、圆规可以开至无限宽,但上面亦不能有刻度。它只可以拉开成之前构造过的长度。
“规”就是圆规,是用来画圆的工具,在我国古代甲骨文中就有
“规”这个字。“矩”就像木工使用的角尺,由长短两尺相交成直角而成,两者间用木杠连接以使其牢固,其中短尺叫勾,长尺叫股。
矩的使用是我国古代的一个发明,山东历城武梁祠石室造像中就有“伏羲氏手执矩,女娲氏手执规”之图形。矩不仅可以画直线、直角,加上刻度可以测量,还可以代替圆规。甲骨文中也有矩字,这可追溯到大禹治水(公元前2000年)前。
《史记》卷二记载大禹治水时“左准绳,右规矩”。赵爽注《周髀算经》中有“禹治洪水,……望山川之形,定高下之势,……乃勾股之所由生也。”意即禹治洪水,要先测量地势的高低,就必定要用勾股的道理。这也说明矩起源于很远的中国古代。
春秋时代也有不少著作涉及规矩的论述,《墨子》卷七中说“轮匠(制造车子的工匠)执其规矩,以度天下之方圆。”《孟子》卷四中说“离娄(传说中目力非常强的人)之明,公输子(即鲁班,传说木匠的祖师)之巧,不以规矩,不能成方圆。”可见,在春秋战国时期,规矩已被广泛地用于作图、制作器具了。由于我国古代的矩上已有刻度,因此使用范围较广,具有较大的实用性。
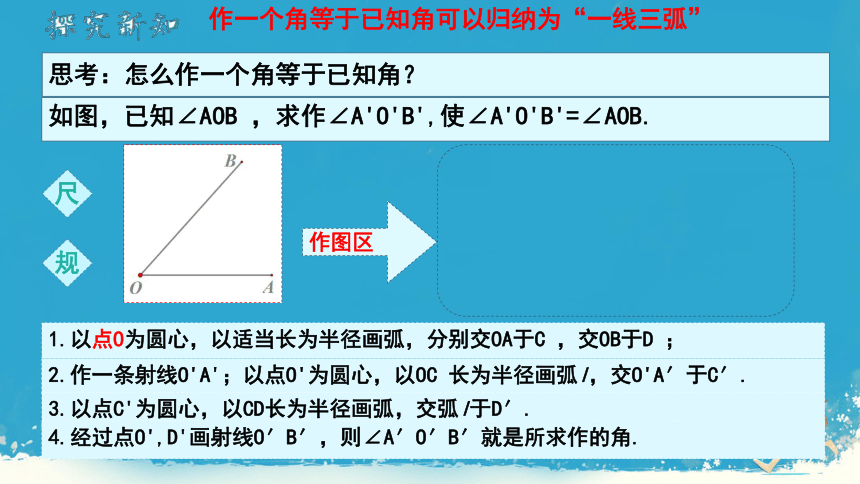
思考:怎么作一个角等于已知角?
如图,已知∠AOB ,求作∠A'O'B',使∠A'O'B'=∠AOB.
尺
规
作图区
2.作一条射线O'A';以点O'为圆心,以OC 长为半径画弧l,交O'A′于C′.
1.以点O为圆心,以适当长为半径画弧,分别交OA于C ,交OB于D ;
3.以点C'为圆心,以CD长为半径画弧,交弧l于D′.
4.经过点O',D'画射线O′B′,则∠A′O′B′就是所求作的角.
作一个角等于已知角可以归纳为“一线三弧”
你能证明上题作图的正确性吗
注:写作法时,不必重复作图的详细过程,只用一句话概括叙述就可以了.如:作线段××=××;作∠×××=∠×××;作线段××的垂直平分线××等。
常用的作图语言
(1)过点×、×作线段或射线、直线;
(2)连结两点×、×;
(3)在线段×或射线×上截取××=××;
(4)以点×为圆心,以××的长为半径作圆(或画弧),交××于点×;
(5)延长××到点×,使××=××.
返回小结
例2 已知线段AB,用直尺和圆规作线段AB的垂直平分线.
(1) 分别以A、B 两点为圆心,以大于AB的一半的长为半径画弧,两弧交于C、D 两点;
(2)过点C、D 作直线CD,直线CD即为所求作线段AB的垂直平分线.
作法:
尺
规
1.完成下面的尺规作图.
(1)如图,已知∠α和∠β,用直尺和圆规作∠ABC,使∠ABC=∠α+∠β.
尺
规
作图区
1.完成下面的尺规作图.
(2)如图,已知线段a,c和∠α,用直尺和圆规作△ABC,使∠ABC=∠α,AB=c,BC=a.
尺
规
作图区
小窍门:两边夹角先作角
例3 已知:∠α,∠β,线段a(如图).
用直尺和圆规作△ABC,使∠A=∠α,∠B=∠β,AB=a.
请按照给出的作法作出相应的图形.
(1)作一条线段AB=a;
(2)分别以A,B为顶点,在AB的同侧作作∠DAB=∠α,∠EBA=∠β,DA与EB相交于点C。
作法:
△则ABC就是求所作的三角形。
尺
规
小窍门: 两角夹边先作边.
2.我们会用三角尺过已知直线外一点作已知直线的垂线.
你能用直尺和圆规完成这一作图吗 若能,说出你的作法.
已知:直线l和直线外一点A.
求作:过点A垂直直线l的直线.
作法:(1) 以点A为圆心,适当长为半径作弧交直线l于B,C两点.
(2) 分别以B,C为圆心,大于BC的一半长为半径画弧,交于点D(不与点A重合).
(3) 过点A,D作直线.直线AD就是所求作的直线l的垂线。
尺
规
3.如图,直线l表示一条公路,点A,B表示两个村庄.现要在公路l上建一个加油站,并使加油站到两个村庄A,B的距离相等.加油站应建在何处 在图上标出加油站的位置,并说明理由.
作法:连结AB,作AB的垂直平分线,交l于点P.加油站应建在P处.理由:线段垂直平分线上的点到线段两端点的距离相等。
尺
规
1.如图,下列四种基本尺规作图分别表示:
①作一个角等于已知角; ②作一个角的平分线;
③作一条线段的垂直平分线; ④过直线外一点P作已知直线的垂线.
对应选项中作法错误的是( )
A.① B.② C.③ D.④
C
2.下列尺规作图,能判断AD是△ABC边上的高的是( )
B
作一个角等于已知角可以归纳为“一线三弧”
只用没有刻度的直尺和圆规作图称为尺规作图.
作三角形小窍门:两边夹角先作角,两角夹边先作边.
要熟悉常用的作图语言
P36-39
已知:线段a,求作一条线段等于a.
(3)在射线AC 上截取AB =a ,则线段 AB 就是所要画的线段.
(1)先画射线AC;
(2)用圆规量出线段a的长;
尺规作法:
尺
规
作图区
据传为了显示谁的逻辑思维能力更强,古希腊人限制了几何作图的工具,结果一些普通的画图题让数学家苦苦思索了两千多年.尺规作图特有的魅力,使无数人沉湎其中。
想一想:你知道什么是尺规作图吗?尺规的基本作用分别是什么?
只用没有刻度的直尺和圆规作图称为尺规作图.
尺规作图的工具只能是直尺和圆规,其中直尺用来作直线、线段、射线或延长线段等;圆规用来作圆或圆孤等.
值得注意的是直尺是没有刻度的或不考虑刻度的存在.
尺规作图是指用无刻度的直尺和圆规作图。尺规作图是起源于古希腊的数学课题。只使用圆规和直尺,并且只准许使用有限次,来解决不同的平面几何作图题。尺规作图使用的直尺和圆规带有想象性质,跟现实中的并非完全相同:
1、直尺必须没有刻度,无限长,且只能使用直尺的固定一侧。只可以用它来将两个点连在一起,不可以在上画刻度;
2、圆规可以开至无限宽,但上面亦不能有刻度。它只可以拉开成之前构造过的长度。
“规”就是圆规,是用来画圆的工具,在我国古代甲骨文中就有
“规”这个字。“矩”就像木工使用的角尺,由长短两尺相交成直角而成,两者间用木杠连接以使其牢固,其中短尺叫勾,长尺叫股。
矩的使用是我国古代的一个发明,山东历城武梁祠石室造像中就有“伏羲氏手执矩,女娲氏手执规”之图形。矩不仅可以画直线、直角,加上刻度可以测量,还可以代替圆规。甲骨文中也有矩字,这可追溯到大禹治水(公元前2000年)前。
《史记》卷二记载大禹治水时“左准绳,右规矩”。赵爽注《周髀算经》中有“禹治洪水,……望山川之形,定高下之势,……乃勾股之所由生也。”意即禹治洪水,要先测量地势的高低,就必定要用勾股的道理。这也说明矩起源于很远的中国古代。
春秋时代也有不少著作涉及规矩的论述,《墨子》卷七中说“轮匠(制造车子的工匠)执其规矩,以度天下之方圆。”《孟子》卷四中说“离娄(传说中目力非常强的人)之明,公输子(即鲁班,传说木匠的祖师)之巧,不以规矩,不能成方圆。”可见,在春秋战国时期,规矩已被广泛地用于作图、制作器具了。由于我国古代的矩上已有刻度,因此使用范围较广,具有较大的实用性。
思考:怎么作一个角等于已知角?
如图,已知∠AOB ,求作∠A'O'B',使∠A'O'B'=∠AOB.
尺
规
作图区
2.作一条射线O'A';以点O'为圆心,以OC 长为半径画弧l,交O'A′于C′.
1.以点O为圆心,以适当长为半径画弧,分别交OA于C ,交OB于D ;
3.以点C'为圆心,以CD长为半径画弧,交弧l于D′.
4.经过点O',D'画射线O′B′,则∠A′O′B′就是所求作的角.
作一个角等于已知角可以归纳为“一线三弧”
你能证明上题作图的正确性吗
注:写作法时,不必重复作图的详细过程,只用一句话概括叙述就可以了.如:作线段××=××;作∠×××=∠×××;作线段××的垂直平分线××等。
常用的作图语言
(1)过点×、×作线段或射线、直线;
(2)连结两点×、×;
(3)在线段×或射线×上截取××=××;
(4)以点×为圆心,以××的长为半径作圆(或画弧),交××于点×;
(5)延长××到点×,使××=××.
返回小结
例2 已知线段AB,用直尺和圆规作线段AB的垂直平分线.
(1) 分别以A、B 两点为圆心,以大于AB的一半的长为半径画弧,两弧交于C、D 两点;
(2)过点C、D 作直线CD,直线CD即为所求作线段AB的垂直平分线.
作法:
尺
规
1.完成下面的尺规作图.
(1)如图,已知∠α和∠β,用直尺和圆规作∠ABC,使∠ABC=∠α+∠β.
尺
规
作图区
1.完成下面的尺规作图.
(2)如图,已知线段a,c和∠α,用直尺和圆规作△ABC,使∠ABC=∠α,AB=c,BC=a.
尺
规
作图区
小窍门:两边夹角先作角
例3 已知:∠α,∠β,线段a(如图).
用直尺和圆规作△ABC,使∠A=∠α,∠B=∠β,AB=a.
请按照给出的作法作出相应的图形.
(1)作一条线段AB=a;
(2)分别以A,B为顶点,在AB的同侧作作∠DAB=∠α,∠EBA=∠β,DA与EB相交于点C。
作法:
△则ABC就是求所作的三角形。
尺
规
小窍门: 两角夹边先作边.
2.我们会用三角尺过已知直线外一点作已知直线的垂线.
你能用直尺和圆规完成这一作图吗 若能,说出你的作法.
已知:直线l和直线外一点A.
求作:过点A垂直直线l的直线.
作法:(1) 以点A为圆心,适当长为半径作弧交直线l于B,C两点.
(2) 分别以B,C为圆心,大于BC的一半长为半径画弧,交于点D(不与点A重合).
(3) 过点A,D作直线.直线AD就是所求作的直线l的垂线。
尺
规
3.如图,直线l表示一条公路,点A,B表示两个村庄.现要在公路l上建一个加油站,并使加油站到两个村庄A,B的距离相等.加油站应建在何处 在图上标出加油站的位置,并说明理由.
作法:连结AB,作AB的垂直平分线,交l于点P.加油站应建在P处.理由:线段垂直平分线上的点到线段两端点的距离相等。
尺
规
1.如图,下列四种基本尺规作图分别表示:
①作一个角等于已知角; ②作一个角的平分线;
③作一条线段的垂直平分线; ④过直线外一点P作已知直线的垂线.
对应选项中作法错误的是( )
A.① B.② C.③ D.④
C
2.下列尺规作图,能判断AD是△ABC边上的高的是( )
B
作一个角等于已知角可以归纳为“一线三弧”
只用没有刻度的直尺和圆规作图称为尺规作图.
作三角形小窍门:两边夹角先作角,两角夹边先作边.
要熟悉常用的作图语言
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
