第2章 特殊三角形 综合复习课件(共18张PPT) 2024-2025学年浙教版数学八年级上册
文档属性
| 名称 | 第2章 特殊三角形 综合复习课件(共18张PPT) 2024-2025学年浙教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 20:42:33 | ||
图片预览





文档简介
(共18张PPT)
第21课 特殊三角形
复习目标:
1、全面梳理有关等腰三角形,等边三角形,直角三角形,线段垂直平分线的相关概念,理解并掌握它们的性质和判定方法,熟练运用性质及判定解题;
2、会用勾股定理解决简单的计算问题,并会用它的逆定理判定直角三角形;
3、理解特殊三角形边角方面的内在联系,并能从不同角度识别特殊三角形,体会事物之间相互转换的特点;
4、在问题解决过程中,渗透一般与特殊、转化、分类讨论等重要的数学思想方法。
线段的垂直平分线
(1)等边对等角;(2)“三线合一”;(3)轴对称.
(1)具有等腰三角形所有的性质;
(2)三边相等;(3)三个角相等,都等于600.
(1)两个锐角互余;(2)两直角边的平方和等于斜边的平方;(3)斜边上的中线等于斜边的一半.
(1)具有等腰三角形与直角三角形所有的性质;(2)两锐角为450.
300角所对的直角边为斜边的一半.
特殊三角形的性质:
1、等腰三角形的性质:
2、等边三角形的性质:
3、直角三角形的性质:
4、等腰直角三角形性质:
5、有一个锐角为300的直角三角形:
特殊三角形的判定:
(1)有两边相等的三角形;(2)有两个角相等的三角形(等角对等边).
(1)三边相等的三角形;(2)三个角相等的三角形;(3)有一个角是600的等腰三角形.
(1)有一个角是直角的三角形;(2)两个锐角互余的三角形;(3)两边平方和等于第三边的平方(勾股定理逆定理)的三角形.
既是等腰三角形又是直角三角形。
1、等腰三角形的判定:
2、等边三角形的判定:
3、直角三角形的判定:
4、等腰直角三角形的判定方法:
线段的垂直平分线:
1、概念:垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线(简称中垂线).
2、性质:(1)线段垂直平分线上的点到线段两个端点的距离相等;(2)线段既是轴对称图形双是中心对称图形①对称轴是线段所在的直线或线段的垂直平分线;②对称中心是线段的中点.
3、判定:到线段两个端点距离相等的点在线段的垂直平分线上。
证明线段垂直平分线的书写过程:如右图
∵CA=CB
∴点C在线段AB的垂直平分线上,
∵DA=DB
∴点D在线段AB的垂直平分线上,
∴CD垂直平分AB
基础过关题:
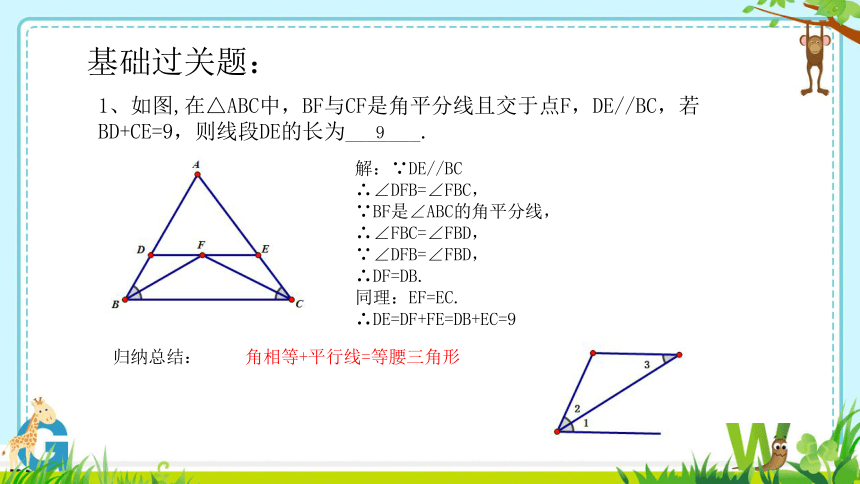
1、如图,在△ABC中,BF与CF是角平分线且交于点F,DE//BC,若BD+CE=9,则线段DE的长为_______.
解:∵DE//BC
∴∠DFB=∠FBC,
∵BF是∠ABC的角平分线,
∴∠FBC=∠FBD,
∵∠DFB=∠FBD,
∴DF=DB.
同理:EF=EC.
∴DE=DF+FE=DB+EC=9
归纳总结:
角相等+平行线=等腰三角形
9
基础过关题:
2、如图,线段AB的长为4,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形ACD和BCE,连结DE,则DE长的最小值是________.
∵根据二次函数的最值,
∴当x=2时,DE取得最小值为2.
基础过关题:
3、在平静的水面上,有一枝荷花,高出水面1米,一阵风吹过来,荷花被吹到一边,花朵齐及水面,已知荷花移动的水平距离为2米,问这里的水深是______米。
解:如图设水深BD为x米;
在Rt△BCD中,BC=(x+1)米,CD=2米;
经典例题:
例1:如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O,
(1)求证:OB=OC;
(2)若∠ABC=50°,求∠BOC的度数。
解:(1)证明:∵AB=AC
∴∠ABC=∠ACB,
∵BD、CE是三角形的两条高线,
∴∠BEC=∠BDC=90°
∴△BEC≌△CDB
∴∠DBC=∠ECB,BE=CD
在△BOE和△COD中
∵∠BOE=∠COD,BE=CD,∠BEO=∠CDO=90°
∴△BOE≌△COD
∴OB=OC
(2)∵∠ABC=50°,AB=AC,
∴∠A=180°-2×50°=80°,
∴∠DOE+∠A=180°
∴∠BOC=∠DOE=180°-80°=100°
经典例题:
例2:如图,矩形ABCD中,AB=3,BC=4,点E是BC边一点,连结AE,把∠B沿AE折叠,使点B落在点B'处,当△CEB'为直角三角形时,求BE的长。
经典例题:
例2:如图,矩形ABCD中,AB=3,BC=4,点E是BC边一点,连结AE,把∠B沿AE折叠,使点B落在点B'处,当△CEB'为直角三角形时,求BE的长。
解:(1)当∠B’EC=90°时,如图,
∴∠BEB’=90°,
∵矩形ABCD沿AE折叠,使点B落在点B’处,
∴∠BEA=∠B’EA=45°
∴B’E=AB=3;
经典例题:
例2:如图,矩形ABCD中,AB=3,BC=4,点E是BC边一点,连结AE,把∠B沿AE折叠,使点B落在点B'处,当△CEB'为直角三角形时,求BE的长。
(2)当∠EB’C=90°时,
在Rt△ABC中,∵AB=3,BC=4
∴AC=5
∵矩形ABCD沿AE折叠,使点B落在点B’处,
∴∠B=∠AB’E=90°,EB=EB’,AB’=AB=3,
∴点A、B’、C共线,即点B’在AC上, CB’=AC-AB’=5-3=2
设BE=x,则EB’=x,CE=4-x,
在Rt△CEB’中,∵EB’2+CB’2=CE2,
∴x2+22=(4-x)2,
解之得:x=1.5
即BE=1.5
(3)当∠B’CE=90°时,点B不存在(舍)
综上所述,BE的长为3或1.5.
经典例题:
例3:在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点 B的对应点为点D,点C的对应点为点E,连结BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F,
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
解:(1)①∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AB=AD,∠BAD=60°,
∴△ABD是等边三角形;
②由①得△ABD是等边三角形,
∴AB=AD
∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AC=AE,BC=DE,
又∵AC=BC
∴EA=ED
∴点B、E在AD的中垂线上,
∴BE垂直平分AD,
∵点F在AD的垂直平分线上,
∴BF⊥AD,AF=DF
经典例题:
例3:在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点 B的对应点为点D,点C的对应点为点E,连结BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F,
③请直接写出BE的长.
解:③由②知BF⊥AD,AF=DF
∴AF=DF=3
∵AE=AC=5
∴EF=4
经典例题:
例3:在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点 B的对应点为点D,点C的对应点为点E,连结BD,BE.
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连结CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
课堂小结:
1、本节课学了哪些知识?掌握了哪些解决问题的方法?
2、在解决问题的过程中用了哪些数学思想方法?
课堂练习:
层层递进:83-84页
第21课 特殊三角形
复习目标:
1、全面梳理有关等腰三角形,等边三角形,直角三角形,线段垂直平分线的相关概念,理解并掌握它们的性质和判定方法,熟练运用性质及判定解题;
2、会用勾股定理解决简单的计算问题,并会用它的逆定理判定直角三角形;
3、理解特殊三角形边角方面的内在联系,并能从不同角度识别特殊三角形,体会事物之间相互转换的特点;
4、在问题解决过程中,渗透一般与特殊、转化、分类讨论等重要的数学思想方法。
线段的垂直平分线
(1)等边对等角;(2)“三线合一”;(3)轴对称.
(1)具有等腰三角形所有的性质;
(2)三边相等;(3)三个角相等,都等于600.
(1)两个锐角互余;(2)两直角边的平方和等于斜边的平方;(3)斜边上的中线等于斜边的一半.
(1)具有等腰三角形与直角三角形所有的性质;(2)两锐角为450.
300角所对的直角边为斜边的一半.
特殊三角形的性质:
1、等腰三角形的性质:
2、等边三角形的性质:
3、直角三角形的性质:
4、等腰直角三角形性质:
5、有一个锐角为300的直角三角形:
特殊三角形的判定:
(1)有两边相等的三角形;(2)有两个角相等的三角形(等角对等边).
(1)三边相等的三角形;(2)三个角相等的三角形;(3)有一个角是600的等腰三角形.
(1)有一个角是直角的三角形;(2)两个锐角互余的三角形;(3)两边平方和等于第三边的平方(勾股定理逆定理)的三角形.
既是等腰三角形又是直角三角形。
1、等腰三角形的判定:
2、等边三角形的判定:
3、直角三角形的判定:
4、等腰直角三角形的判定方法:
线段的垂直平分线:
1、概念:垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线(简称中垂线).
2、性质:(1)线段垂直平分线上的点到线段两个端点的距离相等;(2)线段既是轴对称图形双是中心对称图形①对称轴是线段所在的直线或线段的垂直平分线;②对称中心是线段的中点.
3、判定:到线段两个端点距离相等的点在线段的垂直平分线上。
证明线段垂直平分线的书写过程:如右图
∵CA=CB
∴点C在线段AB的垂直平分线上,
∵DA=DB
∴点D在线段AB的垂直平分线上,
∴CD垂直平分AB
基础过关题:
1、如图,在△ABC中,BF与CF是角平分线且交于点F,DE//BC,若BD+CE=9,则线段DE的长为_______.
解:∵DE//BC
∴∠DFB=∠FBC,
∵BF是∠ABC的角平分线,
∴∠FBC=∠FBD,
∵∠DFB=∠FBD,
∴DF=DB.
同理:EF=EC.
∴DE=DF+FE=DB+EC=9
归纳总结:
角相等+平行线=等腰三角形
9
基础过关题:
2、如图,线段AB的长为4,C为AB上一个动点,分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形ACD和BCE,连结DE,则DE长的最小值是________.
∵根据二次函数的最值,
∴当x=2时,DE取得最小值为2.
基础过关题:
3、在平静的水面上,有一枝荷花,高出水面1米,一阵风吹过来,荷花被吹到一边,花朵齐及水面,已知荷花移动的水平距离为2米,问这里的水深是______米。
解:如图设水深BD为x米;
在Rt△BCD中,BC=(x+1)米,CD=2米;
经典例题:
例1:如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O,
(1)求证:OB=OC;
(2)若∠ABC=50°,求∠BOC的度数。
解:(1)证明:∵AB=AC
∴∠ABC=∠ACB,
∵BD、CE是三角形的两条高线,
∴∠BEC=∠BDC=90°
∴△BEC≌△CDB
∴∠DBC=∠ECB,BE=CD
在△BOE和△COD中
∵∠BOE=∠COD,BE=CD,∠BEO=∠CDO=90°
∴△BOE≌△COD
∴OB=OC
(2)∵∠ABC=50°,AB=AC,
∴∠A=180°-2×50°=80°,
∴∠DOE+∠A=180°
∴∠BOC=∠DOE=180°-80°=100°
经典例题:
例2:如图,矩形ABCD中,AB=3,BC=4,点E是BC边一点,连结AE,把∠B沿AE折叠,使点B落在点B'处,当△CEB'为直角三角形时,求BE的长。
经典例题:
例2:如图,矩形ABCD中,AB=3,BC=4,点E是BC边一点,连结AE,把∠B沿AE折叠,使点B落在点B'处,当△CEB'为直角三角形时,求BE的长。
解:(1)当∠B’EC=90°时,如图,
∴∠BEB’=90°,
∵矩形ABCD沿AE折叠,使点B落在点B’处,
∴∠BEA=∠B’EA=45°
∴B’E=AB=3;
经典例题:
例2:如图,矩形ABCD中,AB=3,BC=4,点E是BC边一点,连结AE,把∠B沿AE折叠,使点B落在点B'处,当△CEB'为直角三角形时,求BE的长。
(2)当∠EB’C=90°时,
在Rt△ABC中,∵AB=3,BC=4
∴AC=5
∵矩形ABCD沿AE折叠,使点B落在点B’处,
∴∠B=∠AB’E=90°,EB=EB’,AB’=AB=3,
∴点A、B’、C共线,即点B’在AC上, CB’=AC-AB’=5-3=2
设BE=x,则EB’=x,CE=4-x,
在Rt△CEB’中,∵EB’2+CB’2=CE2,
∴x2+22=(4-x)2,
解之得:x=1.5
即BE=1.5
(3)当∠B’CE=90°时,点B不存在(舍)
综上所述,BE的长为3或1.5.
经典例题:
例3:在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点 B的对应点为点D,点C的对应点为点E,连结BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F,
①求证:△ABD是等边三角形;
②求证:BF⊥AD,AF=DF;
解:(1)①∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AB=AD,∠BAD=60°,
∴△ABD是等边三角形;
②由①得△ABD是等边三角形,
∴AB=AD
∵△ABC绕点A顺时针方向旋转60°得到△ADE,
∴AC=AE,BC=DE,
又∵AC=BC
∴EA=ED
∴点B、E在AD的中垂线上,
∴BE垂直平分AD,
∵点F在AD的垂直平分线上,
∴BF⊥AD,AF=DF
经典例题:
例3:在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点 B的对应点为点D,点C的对应点为点E,连结BD,BE.
(1)如图,当α=60°时,延长BE交AD于点F,
③请直接写出BE的长.
解:③由②知BF⊥AD,AF=DF
∴AF=DF=3
∵AE=AC=5
∴EF=4
经典例题:
例3:在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点 B的对应点为点D,点C的对应点为点E,连结BD,BE.
(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连结CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接写出BE+CE的值.
课堂小结:
1、本节课学了哪些知识?掌握了哪些解决问题的方法?
2、在解决问题的过程中用了哪些数学思想方法?
课堂练习:
层层递进:83-84页
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
