浙教版数学七年级上册2.4 有理数的除法 精品同步练习(含解析)
文档属性
| 名称 | 浙教版数学七年级上册2.4 有理数的除法 精品同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 07:04:02 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版七年级上册数学 2.4 有理数的除法 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.如果两个数的和是正数,商是负数,那么这两个数的积是( )
A.正数 B.负数 C.零 D.以上三种结论都有可能
2.a是不为2的有理数,我们把称为a的“哈利数”.如:3的“哈利数”是=﹣2,﹣2的“哈利数”是,已知a1=3,a2是a1的“哈利数”,a3是a2的“哈利数”,a4是a3的“哈利数”,…,依此类推,则a2019=( )
A.3 B.﹣2 C. D.
3.已知表示两个非零的实数,则的值不可能是( )
A.2 B.–2 C.1 D.0
4.下列等式或不等式中:①;②;③;④,表示a、b异号的个数有( )
A.0个 B.1个 C.2个 D.3个
5.若a、b都是有理数且都不为零,则式子 值为( )
A.0或﹣2 B.2或﹣2 C.0或2 D.0或±2
6.式子的值等于( )
A. B. C.或 D.3或1
7.下列说法:①若a、b互为相反数,则a+b=0;②若a+b=0,则a、b互为相反数;③若a、b互为相反数,则;④若,则a、b互为相反数.其中正确的结论是( ).
A.②③④ B.①②③ C.①②④ D.①②
8.下列说法:
①2018个有理数相乘,其中负数有2005个,那么所得的积为负数
②若m满足|m|+m=0则m<0
③有理数的倒数是
④若三个有理数a,b,c满足=-1,则
其中正确的是有( )个
A.0 B.1 C.2 D.3
9.己知a、b为有理数,且ab>0,则的值是 ( )
A.3 B.-1 C.-3或1 D.3或-1
10.若1<x<2,则的值是( )
A.﹣3 B.﹣1 C.2 D.1
二、填空题(本大题共5小题,每小题4分,共20分。)
1.在数轴上有理数a,分别用点A,A1表示,我们称点A1是点A的“差倒数点”.已知数轴上点A的差倒数点为点A1;点A1的差倒数点为点A2;点A2的差倒数点为点A3…这样在数轴上依次得到点A,A1,A2,A3,…,An.若点A,A1,A2,A3,…,An在数轴上分别表示的有理数为a,a1、a2、a3、…,an.则当a时,代数式a1+a2+a3+…+a2020的值为______.
2.三个有理数a、b、c满足abc>0,则的值为________.
3.一个数的是,则这个数是______.
4..如图,连接在一起的两个正方形的边长都为1cm,现有一个微型机器人由点A开始按从A→B→C→D→E→F→C→G→A…的顺序沿正方形的边循环移动.当微型机器人移动了2018cm时,它停在_____点.
5..拓展探索:有若干个数,第一个数记为,第二个数记为,第三个数记为,…,第个数记为,若,从第二个数起,每个数都等于1与它前面那个数的差的倒数,如:,…如此计算,_______,______;根据你的推断,_______.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
1.已知++=-1,试求+++的值.
2.若a,b互为相反数,c,d互为倒数,m的绝对值是2,求(a+b+cd)m﹣cd的值.
3.已知,,均为非零有理数,且满足,求的值.
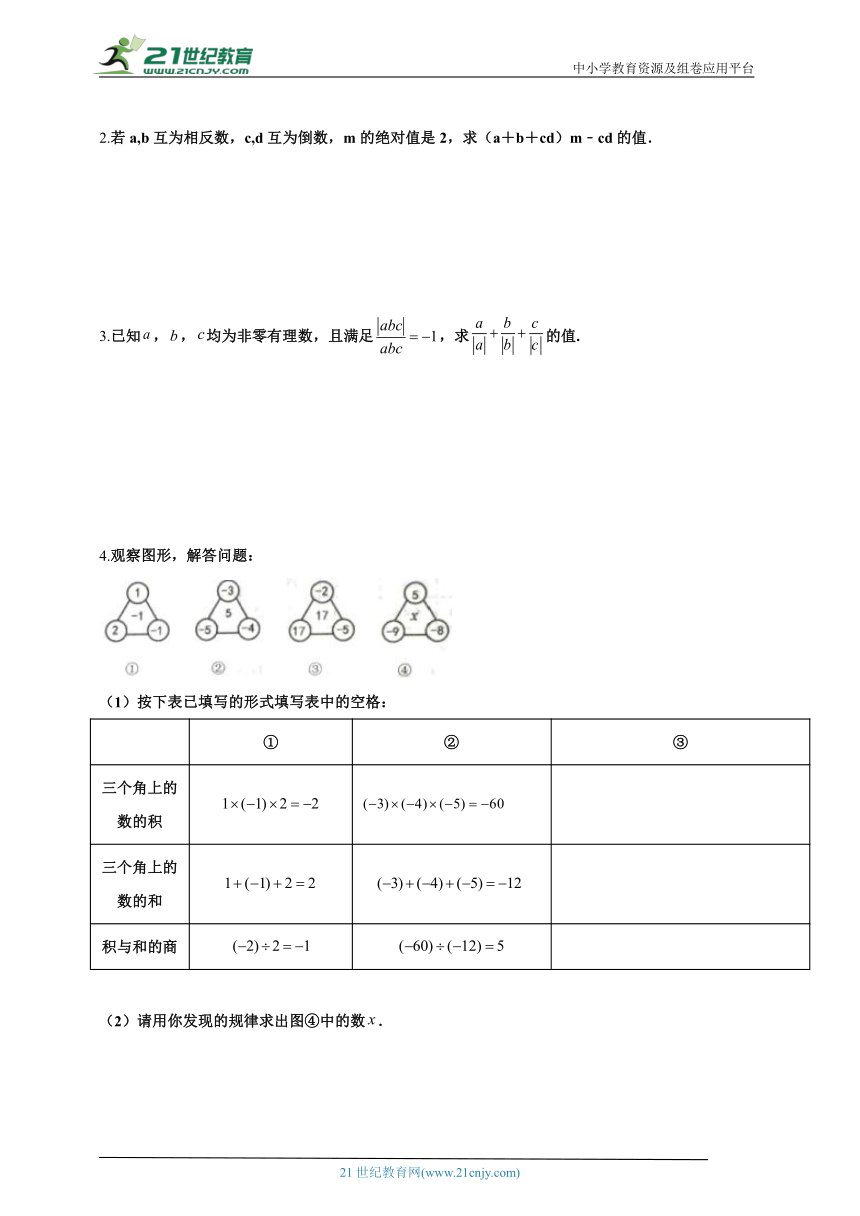
4.观察图形,解答问题:
(1)按下表已填写的形式填写表中的空格:
① ② ③
三个角上的数的积
三个角上的数的和
积与和的商
(2)请用你发现的规律求出图④中的数.
5.小刘、小张两位同学玩数学游戏,小刘说“任意选定一个数,然后按下列步骤进行计算:加上20,乘2,减去4,除以2,再减去你所选定的数”,小张说“不用算了,无论我选什么数,结果总是18”,小张说得对吗?说明理由.
答案解析
选择题
1.答案】B
【解析】
【分析】
根据两个数的积是负数得到两个数异号,而两个数的和是正数,由此即可判定这两个数的符号.
【详解】
解:∵两个数的商是负数,
∴两个数异号,而两个数的和是正数,
∴正数的绝对值大于负数的绝对值.
∴这两个数的积是负数.
故选:B.
2.【答案】C
【分析】
分别求出数列的前5个数得出该数列每4个数为一周期循环,据此可得答案.
【详解】
∵a1=3,
∴a2==﹣2,
a3=,
a4=,
a5=,
∴该数列每4个数为1周期循环,
∵2019÷4=504…3,
∴a2019=a3=.
故选:C.
3.【答案】C
【详解】
∵当时,;当时,;
当时,;当时,;
∴①当时,;
②当时,;
③当时,;
④当时,;
∴综上所述,的值可能为2,-2,0,不可能为1.
故选C.
4.【答案】C
【分析】
根据有理数的加法、乘法、绝对值运算、除法逐个判断即可得.
【详解】
①当时,,但同号;
②,则异号;
③当时,,但同号;
④因为,
所以分以下四种情况:
当时,,
当时,,
当时,,
当时,,
则只有当异号时,;
综上,表示异号的个数有2个,
故选:C.
5.【答案】D
【解析】
试题解析:分情况讨论:
①a>0,b>0;
则式子=1﹣1=0,
②a>0,b<0或a<0,b>0,
则式子=1﹣(﹣1)=2或式子=﹣1﹣1=﹣2
③a<0,b<0,
则式子=﹣1﹣(﹣1)=0.
所以式子的值是2,0或﹣2.
故选D.
6.【答案】C
【解析】
由题意可知:a、b、c的值都不为0.
当时,;当时,;即的值为1或-1.
同理可得:的值为1或-1,的值为1或-1;
因此原式的值共有以下四种情况:
(1)当三个式子的值都为1时,原式=3;
(2)当三个式子的值都为-1时,原式=-3;
(3)当三个式子中有两个的值为1,一个的值为-1时,原式=1;
(4)当三个式子中有两个的值为-1,一个的值为1时,原式=-1;
综上所述,的值为或.
故选C.
7.【答案】C
【详解】
试题分析:根据相反数的定义逐一分析即可得出答案.
解:∵互为相反数的两个数的和为0,
又∵a、b互为相反数,
∴a+b=0,反之也成立,故①、②正确;
∵0的相反数是0,
∴若a=b=0时,无意义,故③错误;
∵= 1,
∴a= b,
∴a、b互为相反数,故④正确;
正确的有①②④.
故选C.
8.【答案】A
【分析】
利用有理数的乘除法法则,绝对值,以及倒数定义判断即可.
【详解】
解:①中当有理数中有0时,结果为0,故①错误;
②中若m满足|m|+m=0则m≤0,故②错误;
③中有理数当分子b=0时,它没有倒数,故③错误;
④中若三个有理数a,b,c满足=-1,可得ab,ac,bc中有两个为负的,
∴a,b,c中负数有2个正数1个或者负数有1个正数2个,
∴或1,故④错误,
故选:A.
9.【答案】D
【解析】
试题分析:根据有理数的乘法,可得a、b同号,分类a、b大于0, a、b都小于0,可化简绝对值,根据有理数的除法,可得答案.
由a、b为有理数,且ab>0,得
b大于0时,,
a、b都小于0时, ,
故选答案:D
10.【答案】D
【分析】
在解绝对值时要考虑到绝对值符号中代数式的正负性,再去掉绝对值符号.
【详解】
解:,
,,,
原式,
故选:.
填空题
1.【答案】
【分析】
先根据已知求出各个数,根据求出的数得出规律,即可得出答案.
【详解】
解:∵a,
∴,
∴,
∴,
∴,
…,
∵2020÷3=673……1,
∴
∴a1+a2+a3+…+a2020
故答案为:.
2.【答案】3或-1
【分析】
a、b、c为三个非零有理数,若,则a、b、c中有两个为负数或者三个都是正数,分两种情况进行讨论即可.
【详解】
a、b、c为三个非零有理数,若,则a、b、c中有一个为负数或者三个都是负数,
若a、b、c中有两个为负数,则原式
a、b、c三个都是正数,则原式
故答案为3或-1.
3.【答案】 8
【分析】
把这个数看成单位“1”,它的对应的数量是,求这个数用除法
【详解】
()÷= 8.
故答案为 8.
4.【答案】C
【分析】
由于沿正方形的边循环移动一圈要走8cm,而2018=8×252+2即微型机器人移动了2018cm时,共走了252圈加2cm,然后得到从A走2cm到C点.
【详解】
∵2018=8×252+2,
∴当微型机器人移动了2018cm时,它停在C点.
故答案为C
5.【答案】; ; .
【分析】
先计算出,的值,再根据特殊情况确定3个一循环即得.
【详解】
∵
∴
∴
∴数据3个一循环
∵
∴
故答案为:,,.
解答题
1.【答案】0.
【解析】
试题分析:已知++=-1,说明a、b、c三数中有两负一正.所以
因为++=-1,所以a,b,c中有两个负数、一个正数.因此可以分情况讨论a、b、c的取值,求出+++的值均为0.
①若a<0,b<0,c>0,则ab>0,bc<0,ca<0,abc>0,所以原式=1-1-1+1=0;
②若a<0,b>0,c<0,则ab<0,bc<0,ca>0,abc>0,所以原式=(-1)-1+1+1=0.
其他几种情况同理可推得ab,bc,ca,abc中有两个正数、两个负数.
所以+++=0.
2.【答案】1或-3.
【解析】
试题分析:
由相反数的定义可知a+b=0;由倒数的定义可知cd=1;由绝对值的定义可知m的值既可以为2也可以为-2. 将待求值的式子中的a+b与cd分别看作一个整体形式代入相应数值,并将m的不同取值分别代入该式求值即可.
试题解析:
因为a,b互为相反数,所以a+b=0,
因为c,d互为倒数,所以cd=1,
因为m的绝对值为2,所以m=2或m=-2.
当m=2时,;
当m=-2时,.
综上所述,(a+b+cd)m-cd的值为1或-3.
3.【答案】1或-3
【分析】
根据可知,的积为负数,则为两正一负或三负;再利用有理数加法、除法法则计算即可.
【详解】
∵
∴为两正一负或三负
当为两正一负时,
当为三个负数时,
4.【答案】(1)③;;. (2)
【分析】
(1)根据图形和表中已填写的形式,即可求出表中的空格.
(2)根据图①②③可知,中间的数是三个角上的数字的乘积与和的商,分别求出三个角上的数字的乘积与和,再相除即可.
【详解】
(1)③
.
(2),,
.
故答案为:-30.
5.【答案】正确
【分析】
设此整数是a,再根据题意列出式子进行计算即可.
【详解】
正确,理由如下:
设此整数是,由题意得
a
=a+20-2
=18,
所以说小张说的对.
答案解析
选择题
1.答案】B
【解析】
【分析】
根据两个数的积是负数得到两个数异号,而两个数的和是正数,由此即可判定这两个数的符号.
【详解】
解:∵两个数的商是负数,
∴两个数异号,而两个数的和是正数,
∴正数的绝对值大于负数的绝对值.
∴这两个数的积是负数.
故选:B.
2.【答案】C
【分析】
分别求出数列的前5个数得出该数列每4个数为一周期循环,据此可得答案.
【详解】
∵a1=3,
∴a2==﹣2,
a3=,
a4=,
a5=,
∴该数列每4个数为1周期循环,
∵2019÷4=504…3,
∴a2019=a3=.
故选:C.
3.【答案】C
【详解】
∵当时,;当时,;
当时,;当时,;
∴①当时,;
②当时,;
③当时,;
④当时,;
∴综上所述,的值可能为2,-2,0,不可能为1.
故选C.
4.【答案】C
【分析】
根据有理数的加法、乘法、绝对值运算、除法逐个判断即可得.
【详解】
①当时,,但同号;
②,则异号;
③当时,,但同号;
④因为,
所以分以下四种情况:
当时,,
当时,,
当时,,
当时,,
则只有当异号时,;
综上,表示异号的个数有2个,
故选:C.
5.【答案】D
【解析】
试题解析:分情况讨论:
①a>0,b>0;
则式子=1﹣1=0,
②a>0,b<0或a<0,b>0,
则式子=1﹣(﹣1)=2或式子=﹣1﹣1=﹣2
③a<0,b<0,
则式子=﹣1﹣(﹣1)=0.
所以式子的值是2,0或﹣2.
故选D.
6.【答案】C
【解析】
由题意可知:a、b、c的值都不为0.
当时,;当时,;即的值为1或-1.
同理可得:的值为1或-1,的值为1或-1;
因此原式的值共有以下四种情况:
(1)当三个式子的值都为1时,原式=3;
(2)当三个式子的值都为-1时,原式=-3;
(3)当三个式子中有两个的值为1,一个的值为-1时,原式=1;
(4)当三个式子中有两个的值为-1,一个的值为1时,原式=-1;
综上所述,的值为或.
故选C.
7.【答案】C
【详解】
试题分析:根据相反数的定义逐一分析即可得出答案.
解:∵互为相反数的两个数的和为0,
又∵a、b互为相反数,
∴a+b=0,反之也成立,故①、②正确;
∵0的相反数是0,
∴若a=b=0时,无意义,故③错误;
∵= 1,
∴a= b,
∴a、b互为相反数,故④正确;
正确的有①②④.
故选C.
8.【答案】A
【分析】
利用有理数的乘除法法则,绝对值,以及倒数定义判断即可.
【详解】
解:①中当有理数中有0时,结果为0,故①错误;
②中若m满足|m|+m=0则m≤0,故②错误;
③中有理数当分子b=0时,它没有倒数,故③错误;
④中若三个有理数a,b,c满足=-1,可得ab,ac,bc中有两个为负的,
∴a,b,c中负数有2个正数1个或者负数有1个正数2个,
∴或1,故④错误,
故选:A.
9.【答案】D
【解析】
试题分析:根据有理数的乘法,可得a、b同号,分类a、b大于0, a、b都小于0,可化简绝对值,根据有理数的除法,可得答案.
由a、b为有理数,且ab>0,得
b大于0时,,
a、b都小于0时, ,
故选答案:D
10.【答案】D
【分析】
在解绝对值时要考虑到绝对值符号中代数式的正负性,再去掉绝对值符号.
【详解】
解:,
,,,
原式,
故选:.
填空题
1.【答案】
【分析】
先根据已知求出各个数,根据求出的数得出规律,即可得出答案.
【详解】
解:∵a,
∴,
∴,
∴,
∴,
…,
∵2020÷3=673……1,
∴
∴a1+a2+a3+…+a2020
故答案为:.
2.【答案】3或-1
【分析】
a、b、c为三个非零有理数,若,则a、b、c中有两个为负数或者三个都是正数,分两种情况进行讨论即可.
【详解】
a、b、c为三个非零有理数,若,则a、b、c中有一个为负数或者三个都是负数,
若a、b、c中有两个为负数,则原式
a、b、c三个都是正数,则原式
故答案为3或-1.
3.【答案】 8
【分析】
把这个数看成单位“1”,它的对应的数量是,求这个数用除法
【详解】
()÷= 8.
故答案为 8.
4.【答案】C
【分析】
由于沿正方形的边循环移动一圈要走8cm,而2018=8×252+2即微型机器人移动了2018cm时,共走了252圈加2cm,然后得到从A走2cm到C点.
【详解】
∵2018=8×252+2,
∴当微型机器人移动了2018cm时,它停在C点.
故答案为C
5.【答案】; ; .
【分析】
先计算出,的值,再根据特殊情况确定3个一循环即得.
【详解】
∵
∴
∴
∴数据3个一循环
∵
∴
故答案为:,,.
解答题
1.【答案】0.
【解析】
试题分析:已知++=-1,说明a、b、c三数中有两负一正.所以
因为++=-1,所以a,b,c中有两个负数、一个正数.因此可以分情况讨论a、b、c的取值,求出+++的值均为0.
①若a<0,b<0,c>0,则ab>0,bc<0,ca<0,abc>0,所以原式=1-1-1+1=0;
②若a<0,b>0,c<0,则ab<0,bc<0,ca>0,abc>0,所以原式=(-1)-1+1+1=0.
其他几种情况同理可推得ab,bc,ca,abc中有两个正数、两个负数.
所以+++=0.
2.【答案】1或-3.
【解析】
试题分析:
由相反数的定义可知a+b=0;由倒数的定义可知cd=1;由绝对值的定义可知m的值既可以为2也可以为-2. 将待求值的式子中的a+b与cd分别看作一个整体形式代入相应数值,并将m的不同取值分别代入该式求值即可.
试题解析:
因为a,b互为相反数,所以a+b=0,
因为c,d互为倒数,所以cd=1,
因为m的绝对值为2,所以m=2或m=-2.
当m=2时,;
当m=-2时,.
综上所述,(a+b+cd)m-cd的值为1或-3.
3.【答案】1或-3
【分析】
根据可知,的积为负数,则为两正一负或三负;再利用有理数加法、除法法则计算即可.
【详解】
∵
∴为两正一负或三负
当为两正一负时,
当为三个负数时,
4.【答案】(1)③;;. (2)
【分析】
(1)根据图形和表中已填写的形式,即可求出表中的空格.
(2)根据图①②③可知,中间的数是三个角上的数字的乘积与和的商,分别求出三个角上的数字的乘积与和,再相除即可.
【详解】
(1)③
.
(2),,
.
故答案为:-30.
5.【答案】正确
【分析】
设此整数是a,再根据题意列出式子进行计算即可.
【详解】
正确,理由如下:
设此整数是,由题意得
a
=a+20-2
=18,
所以说小张说的对.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版七年级上册数学 2.4 有理数的除法 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.如果两个数的和是正数,商是负数,那么这两个数的积是( )
A.正数 B.负数 C.零 D.以上三种结论都有可能
2.a是不为2的有理数,我们把称为a的“哈利数”.如:3的“哈利数”是=﹣2,﹣2的“哈利数”是,已知a1=3,a2是a1的“哈利数”,a3是a2的“哈利数”,a4是a3的“哈利数”,…,依此类推,则a2019=( )
A.3 B.﹣2 C. D.
3.已知表示两个非零的实数,则的值不可能是( )
A.2 B.–2 C.1 D.0
4.下列等式或不等式中:①;②;③;④,表示a、b异号的个数有( )
A.0个 B.1个 C.2个 D.3个
5.若a、b都是有理数且都不为零,则式子 值为( )
A.0或﹣2 B.2或﹣2 C.0或2 D.0或±2
6.式子的值等于( )
A. B. C.或 D.3或1
7.下列说法:①若a、b互为相反数,则a+b=0;②若a+b=0,则a、b互为相反数;③若a、b互为相反数,则;④若,则a、b互为相反数.其中正确的结论是( ).
A.②③④ B.①②③ C.①②④ D.①②
8.下列说法:
①2018个有理数相乘,其中负数有2005个,那么所得的积为负数
②若m满足|m|+m=0则m<0
③有理数的倒数是
④若三个有理数a,b,c满足=-1,则
其中正确的是有( )个
A.0 B.1 C.2 D.3
9.己知a、b为有理数,且ab>0,则的值是 ( )
A.3 B.-1 C.-3或1 D.3或-1
10.若1<x<2,则的值是( )
A.﹣3 B.﹣1 C.2 D.1
二、填空题(本大题共5小题,每小题4分,共20分。)
1.在数轴上有理数a,分别用点A,A1表示,我们称点A1是点A的“差倒数点”.已知数轴上点A的差倒数点为点A1;点A1的差倒数点为点A2;点A2的差倒数点为点A3…这样在数轴上依次得到点A,A1,A2,A3,…,An.若点A,A1,A2,A3,…,An在数轴上分别表示的有理数为a,a1、a2、a3、…,an.则当a时,代数式a1+a2+a3+…+a2020的值为______.
2.三个有理数a、b、c满足abc>0,则的值为________.
3.一个数的是,则这个数是______.
4..如图,连接在一起的两个正方形的边长都为1cm,现有一个微型机器人由点A开始按从A→B→C→D→E→F→C→G→A…的顺序沿正方形的边循环移动.当微型机器人移动了2018cm时,它停在_____点.
5..拓展探索:有若干个数,第一个数记为,第二个数记为,第三个数记为,…,第个数记为,若,从第二个数起,每个数都等于1与它前面那个数的差的倒数,如:,…如此计算,_______,______;根据你的推断,_______.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
1.已知++=-1,试求+++的值.
2.若a,b互为相反数,c,d互为倒数,m的绝对值是2,求(a+b+cd)m﹣cd的值.
3.已知,,均为非零有理数,且满足,求的值.
4.观察图形,解答问题:
(1)按下表已填写的形式填写表中的空格:
① ② ③
三个角上的数的积
三个角上的数的和
积与和的商
(2)请用你发现的规律求出图④中的数.
5.小刘、小张两位同学玩数学游戏,小刘说“任意选定一个数,然后按下列步骤进行计算:加上20,乘2,减去4,除以2,再减去你所选定的数”,小张说“不用算了,无论我选什么数,结果总是18”,小张说得对吗?说明理由.
答案解析
选择题
1.答案】B
【解析】
【分析】
根据两个数的积是负数得到两个数异号,而两个数的和是正数,由此即可判定这两个数的符号.
【详解】
解:∵两个数的商是负数,
∴两个数异号,而两个数的和是正数,
∴正数的绝对值大于负数的绝对值.
∴这两个数的积是负数.
故选:B.
2.【答案】C
【分析】
分别求出数列的前5个数得出该数列每4个数为一周期循环,据此可得答案.
【详解】
∵a1=3,
∴a2==﹣2,
a3=,
a4=,
a5=,
∴该数列每4个数为1周期循环,
∵2019÷4=504…3,
∴a2019=a3=.
故选:C.
3.【答案】C
【详解】
∵当时,;当时,;
当时,;当时,;
∴①当时,;
②当时,;
③当时,;
④当时,;
∴综上所述,的值可能为2,-2,0,不可能为1.
故选C.
4.【答案】C
【分析】
根据有理数的加法、乘法、绝对值运算、除法逐个判断即可得.
【详解】
①当时,,但同号;
②,则异号;
③当时,,但同号;
④因为,
所以分以下四种情况:
当时,,
当时,,
当时,,
当时,,
则只有当异号时,;
综上,表示异号的个数有2个,
故选:C.
5.【答案】D
【解析】
试题解析:分情况讨论:
①a>0,b>0;
则式子=1﹣1=0,
②a>0,b<0或a<0,b>0,
则式子=1﹣(﹣1)=2或式子=﹣1﹣1=﹣2
③a<0,b<0,
则式子=﹣1﹣(﹣1)=0.
所以式子的值是2,0或﹣2.
故选D.
6.【答案】C
【解析】
由题意可知:a、b、c的值都不为0.
当时,;当时,;即的值为1或-1.
同理可得:的值为1或-1,的值为1或-1;
因此原式的值共有以下四种情况:
(1)当三个式子的值都为1时,原式=3;
(2)当三个式子的值都为-1时,原式=-3;
(3)当三个式子中有两个的值为1,一个的值为-1时,原式=1;
(4)当三个式子中有两个的值为-1,一个的值为1时,原式=-1;
综上所述,的值为或.
故选C.
7.【答案】C
【详解】
试题分析:根据相反数的定义逐一分析即可得出答案.
解:∵互为相反数的两个数的和为0,
又∵a、b互为相反数,
∴a+b=0,反之也成立,故①、②正确;
∵0的相反数是0,
∴若a=b=0时,无意义,故③错误;
∵= 1,
∴a= b,
∴a、b互为相反数,故④正确;
正确的有①②④.
故选C.
8.【答案】A
【分析】
利用有理数的乘除法法则,绝对值,以及倒数定义判断即可.
【详解】
解:①中当有理数中有0时,结果为0,故①错误;
②中若m满足|m|+m=0则m≤0,故②错误;
③中有理数当分子b=0时,它没有倒数,故③错误;
④中若三个有理数a,b,c满足=-1,可得ab,ac,bc中有两个为负的,
∴a,b,c中负数有2个正数1个或者负数有1个正数2个,
∴或1,故④错误,
故选:A.
9.【答案】D
【解析】
试题分析:根据有理数的乘法,可得a、b同号,分类a、b大于0, a、b都小于0,可化简绝对值,根据有理数的除法,可得答案.
由a、b为有理数,且ab>0,得
b大于0时,,
a、b都小于0时, ,
故选答案:D
10.【答案】D
【分析】
在解绝对值时要考虑到绝对值符号中代数式的正负性,再去掉绝对值符号.
【详解】
解:,
,,,
原式,
故选:.
填空题
1.【答案】
【分析】
先根据已知求出各个数,根据求出的数得出规律,即可得出答案.
【详解】
解:∵a,
∴,
∴,
∴,
∴,
…,
∵2020÷3=673……1,
∴
∴a1+a2+a3+…+a2020
故答案为:.
2.【答案】3或-1
【分析】
a、b、c为三个非零有理数,若,则a、b、c中有两个为负数或者三个都是正数,分两种情况进行讨论即可.
【详解】
a、b、c为三个非零有理数,若,则a、b、c中有一个为负数或者三个都是负数,
若a、b、c中有两个为负数,则原式
a、b、c三个都是正数,则原式
故答案为3或-1.
3.【答案】 8
【分析】
把这个数看成单位“1”,它的对应的数量是,求这个数用除法
【详解】
()÷= 8.
故答案为 8.
4.【答案】C
【分析】
由于沿正方形的边循环移动一圈要走8cm,而2018=8×252+2即微型机器人移动了2018cm时,共走了252圈加2cm,然后得到从A走2cm到C点.
【详解】
∵2018=8×252+2,
∴当微型机器人移动了2018cm时,它停在C点.
故答案为C
5.【答案】; ; .
【分析】
先计算出,的值,再根据特殊情况确定3个一循环即得.
【详解】
∵
∴
∴
∴数据3个一循环
∵
∴
故答案为:,,.
解答题
1.【答案】0.
【解析】
试题分析:已知++=-1,说明a、b、c三数中有两负一正.所以
因为++=-1,所以a,b,c中有两个负数、一个正数.因此可以分情况讨论a、b、c的取值,求出+++的值均为0.
①若a<0,b<0,c>0,则ab>0,bc<0,ca<0,abc>0,所以原式=1-1-1+1=0;
②若a<0,b>0,c<0,则ab<0,bc<0,ca>0,abc>0,所以原式=(-1)-1+1+1=0.
其他几种情况同理可推得ab,bc,ca,abc中有两个正数、两个负数.
所以+++=0.
2.【答案】1或-3.
【解析】
试题分析:
由相反数的定义可知a+b=0;由倒数的定义可知cd=1;由绝对值的定义可知m的值既可以为2也可以为-2. 将待求值的式子中的a+b与cd分别看作一个整体形式代入相应数值,并将m的不同取值分别代入该式求值即可.
试题解析:
因为a,b互为相反数,所以a+b=0,
因为c,d互为倒数,所以cd=1,
因为m的绝对值为2,所以m=2或m=-2.
当m=2时,;
当m=-2时,.
综上所述,(a+b+cd)m-cd的值为1或-3.
3.【答案】1或-3
【分析】
根据可知,的积为负数,则为两正一负或三负;再利用有理数加法、除法法则计算即可.
【详解】
∵
∴为两正一负或三负
当为两正一负时,
当为三个负数时,
4.【答案】(1)③;;. (2)
【分析】
(1)根据图形和表中已填写的形式,即可求出表中的空格.
(2)根据图①②③可知,中间的数是三个角上的数字的乘积与和的商,分别求出三个角上的数字的乘积与和,再相除即可.
【详解】
(1)③
.
(2),,
.
故答案为:-30.
5.【答案】正确
【分析】
设此整数是a,再根据题意列出式子进行计算即可.
【详解】
正确,理由如下:
设此整数是,由题意得
a
=a+20-2
=18,
所以说小张说的对.
答案解析
选择题
1.答案】B
【解析】
【分析】
根据两个数的积是负数得到两个数异号,而两个数的和是正数,由此即可判定这两个数的符号.
【详解】
解:∵两个数的商是负数,
∴两个数异号,而两个数的和是正数,
∴正数的绝对值大于负数的绝对值.
∴这两个数的积是负数.
故选:B.
2.【答案】C
【分析】
分别求出数列的前5个数得出该数列每4个数为一周期循环,据此可得答案.
【详解】
∵a1=3,
∴a2==﹣2,
a3=,
a4=,
a5=,
∴该数列每4个数为1周期循环,
∵2019÷4=504…3,
∴a2019=a3=.
故选:C.
3.【答案】C
【详解】
∵当时,;当时,;
当时,;当时,;
∴①当时,;
②当时,;
③当时,;
④当时,;
∴综上所述,的值可能为2,-2,0,不可能为1.
故选C.
4.【答案】C
【分析】
根据有理数的加法、乘法、绝对值运算、除法逐个判断即可得.
【详解】
①当时,,但同号;
②,则异号;
③当时,,但同号;
④因为,
所以分以下四种情况:
当时,,
当时,,
当时,,
当时,,
则只有当异号时,;
综上,表示异号的个数有2个,
故选:C.
5.【答案】D
【解析】
试题解析:分情况讨论:
①a>0,b>0;
则式子=1﹣1=0,
②a>0,b<0或a<0,b>0,
则式子=1﹣(﹣1)=2或式子=﹣1﹣1=﹣2
③a<0,b<0,
则式子=﹣1﹣(﹣1)=0.
所以式子的值是2,0或﹣2.
故选D.
6.【答案】C
【解析】
由题意可知:a、b、c的值都不为0.
当时,;当时,;即的值为1或-1.
同理可得:的值为1或-1,的值为1或-1;
因此原式的值共有以下四种情况:
(1)当三个式子的值都为1时,原式=3;
(2)当三个式子的值都为-1时,原式=-3;
(3)当三个式子中有两个的值为1,一个的值为-1时,原式=1;
(4)当三个式子中有两个的值为-1,一个的值为1时,原式=-1;
综上所述,的值为或.
故选C.
7.【答案】C
【详解】
试题分析:根据相反数的定义逐一分析即可得出答案.
解:∵互为相反数的两个数的和为0,
又∵a、b互为相反数,
∴a+b=0,反之也成立,故①、②正确;
∵0的相反数是0,
∴若a=b=0时,无意义,故③错误;
∵= 1,
∴a= b,
∴a、b互为相反数,故④正确;
正确的有①②④.
故选C.
8.【答案】A
【分析】
利用有理数的乘除法法则,绝对值,以及倒数定义判断即可.
【详解】
解:①中当有理数中有0时,结果为0,故①错误;
②中若m满足|m|+m=0则m≤0,故②错误;
③中有理数当分子b=0时,它没有倒数,故③错误;
④中若三个有理数a,b,c满足=-1,可得ab,ac,bc中有两个为负的,
∴a,b,c中负数有2个正数1个或者负数有1个正数2个,
∴或1,故④错误,
故选:A.
9.【答案】D
【解析】
试题分析:根据有理数的乘法,可得a、b同号,分类a、b大于0, a、b都小于0,可化简绝对值,根据有理数的除法,可得答案.
由a、b为有理数,且ab>0,得
b大于0时,,
a、b都小于0时, ,
故选答案:D
10.【答案】D
【分析】
在解绝对值时要考虑到绝对值符号中代数式的正负性,再去掉绝对值符号.
【详解】
解:,
,,,
原式,
故选:.
填空题
1.【答案】
【分析】
先根据已知求出各个数,根据求出的数得出规律,即可得出答案.
【详解】
解:∵a,
∴,
∴,
∴,
∴,
…,
∵2020÷3=673……1,
∴
∴a1+a2+a3+…+a2020
故答案为:.
2.【答案】3或-1
【分析】
a、b、c为三个非零有理数,若,则a、b、c中有两个为负数或者三个都是正数,分两种情况进行讨论即可.
【详解】
a、b、c为三个非零有理数,若,则a、b、c中有一个为负数或者三个都是负数,
若a、b、c中有两个为负数,则原式
a、b、c三个都是正数,则原式
故答案为3或-1.
3.【答案】 8
【分析】
把这个数看成单位“1”,它的对应的数量是,求这个数用除法
【详解】
()÷= 8.
故答案为 8.
4.【答案】C
【分析】
由于沿正方形的边循环移动一圈要走8cm,而2018=8×252+2即微型机器人移动了2018cm时,共走了252圈加2cm,然后得到从A走2cm到C点.
【详解】
∵2018=8×252+2,
∴当微型机器人移动了2018cm时,它停在C点.
故答案为C
5.【答案】; ; .
【分析】
先计算出,的值,再根据特殊情况确定3个一循环即得.
【详解】
∵
∴
∴
∴数据3个一循环
∵
∴
故答案为:,,.
解答题
1.【答案】0.
【解析】
试题分析:已知++=-1,说明a、b、c三数中有两负一正.所以
因为++=-1,所以a,b,c中有两个负数、一个正数.因此可以分情况讨论a、b、c的取值,求出+++的值均为0.
①若a<0,b<0,c>0,则ab>0,bc<0,ca<0,abc>0,所以原式=1-1-1+1=0;
②若a<0,b>0,c<0,则ab<0,bc<0,ca>0,abc>0,所以原式=(-1)-1+1+1=0.
其他几种情况同理可推得ab,bc,ca,abc中有两个正数、两个负数.
所以+++=0.
2.【答案】1或-3.
【解析】
试题分析:
由相反数的定义可知a+b=0;由倒数的定义可知cd=1;由绝对值的定义可知m的值既可以为2也可以为-2. 将待求值的式子中的a+b与cd分别看作一个整体形式代入相应数值,并将m的不同取值分别代入该式求值即可.
试题解析:
因为a,b互为相反数,所以a+b=0,
因为c,d互为倒数,所以cd=1,
因为m的绝对值为2,所以m=2或m=-2.
当m=2时,;
当m=-2时,.
综上所述,(a+b+cd)m-cd的值为1或-3.
3.【答案】1或-3
【分析】
根据可知,的积为负数,则为两正一负或三负;再利用有理数加法、除法法则计算即可.
【详解】
∵
∴为两正一负或三负
当为两正一负时,
当为三个负数时,
4.【答案】(1)③;;. (2)
【分析】
(1)根据图形和表中已填写的形式,即可求出表中的空格.
(2)根据图①②③可知,中间的数是三个角上的数字的乘积与和的商,分别求出三个角上的数字的乘积与和,再相除即可.
【详解】
(1)③
.
(2),,
.
故答案为:-30.
5.【答案】正确
【分析】
设此整数是a,再根据题意列出式子进行计算即可.
【详解】
正确,理由如下:
设此整数是,由题意得
a
=a+20-2
=18,
所以说小张说的对.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
