2024—2025学年浙教版九年级上册 第1章二次函数题型模拟训练(含答案)
文档属性
| 名称 | 2024—2025学年浙教版九年级上册 第1章二次函数题型模拟训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 163.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 00:00:00 | ||
图片预览




文档简介
2024浙江模拟二次函数题型训练
一、选择题
1.将二次函数的图象向左平移m个单位后过点,则m的值为( )
A.2 B.3 C.4 D.5
2.已知二次函数y=a(x+m﹣1)(x﹣m)(a≠0)的图象上有两点A(x1,y1)和B(x2,y2)(其中x1<x2),则( )
A.若a>0,当x1+x2<1时,a(y1﹣y2)<0
B.若a>0,当x1+x2<1时,a(y1﹣y2)>0
C.若a<0,当x1+x2>﹣1时,a(y1﹣y2)<0
D.若a<0,当x1+x2>﹣1时,a(y1﹣y2)>0
3.已知点,,均在抛物线的图象上,且,点和也在此抛物线上,则下列说法正确的是( )
A.若恒成立,则 B.若恒成立,则
C.若恒成立,则 D.若恒成立,则
4.定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min(﹣x2+3,﹣2x}的最大值是( )
A.3 B.2 C.1 D.0
5.对于二次函数y=﹣2x2+mx﹣1,当x<1时,y随x的增大而增大,则满足条件的m的取值范围是( )
A.m≥4 B.m≥3 C.m≥2 D.m≥﹣4
6.已知抛物线和直线交于,两点,其中,且满足,则直线一定经过( )
A.第一、二象限 B.第二、三象限
C.第三、四象限 D.第一、四象限
二、填空题
7.已知二次函数,当时,的最大值为9,则的值为 .
8.已知二次函敞.
(1)若点在该函数图象上,则的值为 .
(2)若点都在该函数图象上,且,则的取值范围为 .
9.已知,为x轴上两点,,为二次函数图象上两点,当时,二次函数y随x增大而减小,若,时,恒成立,则A、B两点的最大距离为 .
三、解答题
10.如图,直线分别交轴、轴于点,,抛物线经过点.
(1)求点的坐标和抛物线的函数表达式;
(2)若抛物线向左平移个单位后经过点,求的值.
11.已知二次函数的图象经过原点O和点,其中.
(1)当时
①求y关于x的函数表达式,并求出当x为何值时,y有最大值,最大值为多少?
②当和时(),函数值相等,求m,n之间的关系式.
(2)当时,在范围内,y是否存在最大值18?若存在,求出相应的t和x的值,若不存在,请说明理由.
12.在平面直角坐标系中,抛物线为常数,且经过和两点.
(1)求和的值用含的代数式表示;
(2)若该抛物线开口向下,且经过,两点,当时,随的增大而减小,求的取值范围;
(3)已知点,,若该抛物线与线段恰有一个公共点时,结合函数图象,求的取值范围.
13.顶点为的二次函数满足以下三个条件的任意两个:
其与轴的交点为;
其与轴的交点为和;
该函数其最大值为.
(1)从以上条件任选两个,求出函数的表达式;
(2)若存在直线,二次函数上的存在一个点,使得等于到直线的距离,求出点的坐标.
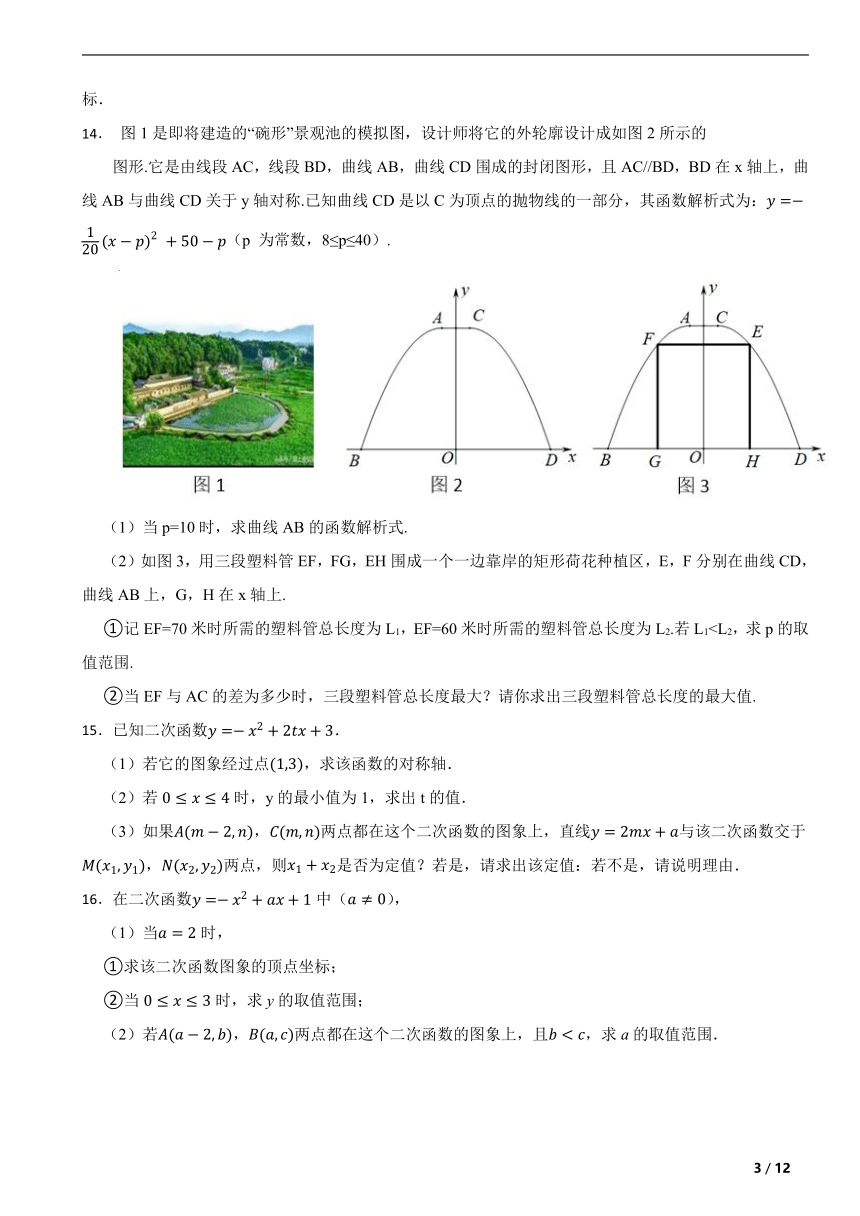
14. 图1是即将建造的“碗形”景观池的模拟图,设计师将它的外轮廓设计成如图2所示的
图形.它是由线段AC,线段BD,曲线AB,曲线CD围成的封闭图形,且AC//BD,BD在x轴上,曲线AB与曲线CD关于y轴对称.已知曲线CD是以C为顶点的抛物线的一部分,其函数解析式为:(p 为常数,8≤p≤40).
(1)当p=10时,求曲线AB的函数解析式.
(2)如图3,用三段塑料管EF,FG,EH围成一个一边靠岸的矩形荷花种植区,E,F分别在曲线CD,曲线AB上,G,H在x轴上.
①记EF=70米时所需的塑料管总长度为L1,EF=60米时所需的塑料管总长度为L2.若L1②当EF与AC的差为多少时,三段塑料管总长度最大?请你求出三段塑料管总长度的最大值.
15.已知二次函数.
(1)若它的图象经过点,求该函数的对称轴.
(2)若时,y的最小值为1,求出t的值.
(3)如果,两点都在这个二次函数的图象上,直线与该二次函数交于,两点,则是否为定值?若是,请求出该定值:若不是,请说明理由.
16.在二次函数中(),
(1)当时,
①求该二次函数图象的顶点坐标;
②当时,求y的取值范围;
(2)若,两点都在这个二次函数的图象上,且,求a的取值范围.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】A
6.【答案】B
7.【答案】
8.【答案】(1)2或-2
(2)-3<b<-2或b>2
9.【答案】8
10.【答案】(1)解:由可知,令,则,
∴点的坐标为,
令,则,
∴点坐标为,
代入抛物线的表达式,得,解得,
∴抛物线的函数表达式为;
(2)解:由(1)得,
∴平移后的抛物线为,将点代入,得,
解得,.
11.【答案】(1)解:当时,,
把、代入得,
,
∴,
∴二次函数为,
∵,
∴当时,有最大值,最大值为;
∵和时,函数值相等,
∴,
整理得,,
∵,则,
∴,
∴.
(2)解:∵二次函数的图象经过原点,
∴,
∴二次函数,
∴对称轴为直线,
∵二次函数的图象经过原点和点,
∴,
当时,对称轴,
∵,
∴时,有最大值,
即,
整理得,,
∴或,
∵
∴,
∴或不合,舍去;
当时,对称轴,
∵,
∴在对称轴的左侧,的值随的增大而增大,
∵,
∴当时,有最大值,
即,
解得,
∴,
∴;
综上,,.
12.【答案】(1)解:把和代入,
得:,
解得:
(2)解:抛物线经过,两点,
抛物线的对称轴为:直线,
抛物线开口向下,当时,随的增大而减小,
,即
(3)解:∵,
∴抛物线为:.
当时,如图,
抛物线与线段只有一个交点,根据抛物线的图象可知,抛物线不经过点N.
故时,,即,
解得:.
当时,若抛物线的顶点在线段上时,则,
解得:,,
当时,,
此时,顶点横坐标满足,符合题意;
∴当时,如图,抛物线与线段只有一个交点,
如图,
当时,.
此时顶点横坐标不满足,不符合题意,舍去;
若抛物线与线段有两个交点,且其中一个交点恰好为点 时,如图④:
把代入,得:
,
解得:,
故当x=2时,y>5,则抛物线不经过点N,和线段有1个交点,
解,
得.
综上所述:的取值范围为:或或时. 抛物线与线段恰有一个公共点.
13.【答案】(1)解:选择条件和,
二次函数与轴的交点为,
,
二次函数与轴的交点为和,
将点和代入函数,
,,
函数的表达式,
答:函数的表达式为:
(2)解:设点的坐标为,
点为函数的顶点,
点的坐标为,
直线,
点到直线的距离,
,
设,
到直线的距离等于,
,
,
或,
点或,
答:点的坐标为:或
14.【答案】(1)解:当p=10时,抛物线CD的解析式为:,
故C坐标为(10,40),
由对称得点A坐标为(-10,40),
∴抛物线AB的解析式为:.
(2)解:①根据题意,设E1(35,y1),E2(30,y2),
∵L1<L2,
∴35+y1<30+y2,
即:,
化简得:65-2p>20,
∴,
∴.
②解:设EF AC=2d,三段塑料管总长度为L,
根据题意可得:,
∴,
化简得:,
当d=10时,L有最大值110.
∴当EF与AC的差为20m时,三段塑料管总长度最大,最大值为110m.
15.【答案】(1)解:将点代入二次函数,得
,
解得:,
对称轴直线为:
;
(2)解:当时,,
∵抛物线开口向下,对称轴为直线,
∴当时,有最大值,
∵时,的最小值为1,
∴当时,,
解得:;
(3)解:是定值,理由:
∵,两点都在这个二次函数的图象上,
,
令,整理得:
,
∵直线与该二次函数交于,两点,
∴是方程的两个根,
是定值.
16.【答案】(1)解:①把代入得,
∴抛物线的顶点坐标为;
②∵当时,y随x的增大而增大,当时.y随x的增大而减小,
∴当时,y有最大值2.
∵当时,;当时,,
∴当时,;
(2)解:抛物线的对称轴为直线,
①当,即时,点B到对称轴的距离小于点A到对称轴的距离,
∴,解得,∴;
②当,即时,点B到对称轴的距离小于点A到对称轴的距离,
∴成立,∴,
③对称轴在点A左侧不合题意,舍去;
综上所述,.
试题分析部分
1、试卷总体分布分析
总分:98分
分值分布 客观题(占比) 14.0(14.3%)
主观题(占比) 84.0(85.7%)
题量分布 客观题(占比) 7(43.8%)
主观题(占比) 9(56.3%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
选择题 6(37.5%) 12.0(12.2%)
填空题 3(18.8%) 6.0(6.1%)
解答题 7(43.8%) 80.0(81.6%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (75.0%)
2 困难 (25.0%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 一次函数图象与坐标轴交点问题 10.0(10.2%) 10
2 二次函数图象的几何变换 12.0(12.2%) 1,10
3 二次函数图象上点的坐标特征 21.0(21.4%) 2,3,8,12
4 二次函数y=ax +bx+c的性质 35.0(35.7%) 2,3,5,8,9,15,16
5 换元法解一元二次方程 10.0(10.2%) 13
6 二次函数图象与系数的关系 17.0(17.3%) 6,12
7 点到直线的距离 10.0(10.2%) 13
8 二次函数的其他应用 10.0(10.2%) 14
9 二次函数y=ax +bx+c与二次函数y=a(x-h) +k的转化 2.0(2.0%) 1
10 二次函数的最值 16.0(16.3%) 4,7,9,11
11 二次函数与一次函数的综合应用 15.0(15.3%) 15
12 待定系数法求二次函数解析式 55.0(56.1%) 10,11,12,13,16
13 坐标系中的两点距离公式 10.0(10.2%) 13
14 二次函数图象与坐标轴的交点问题 2.0(2.0%) 2
1 / 1
一、选择题
1.将二次函数的图象向左平移m个单位后过点,则m的值为( )
A.2 B.3 C.4 D.5
2.已知二次函数y=a(x+m﹣1)(x﹣m)(a≠0)的图象上有两点A(x1,y1)和B(x2,y2)(其中x1<x2),则( )
A.若a>0,当x1+x2<1时,a(y1﹣y2)<0
B.若a>0,当x1+x2<1时,a(y1﹣y2)>0
C.若a<0,当x1+x2>﹣1时,a(y1﹣y2)<0
D.若a<0,当x1+x2>﹣1时,a(y1﹣y2)>0
3.已知点,,均在抛物线的图象上,且,点和也在此抛物线上,则下列说法正确的是( )
A.若恒成立,则 B.若恒成立,则
C.若恒成立,则 D.若恒成立,则
4.定义符号min{a,b}的含义为:当a≥b时min{a,b}=b;当a<b时min{a,b}=a.如min{1,﹣3}=﹣3,min{﹣4,﹣2}=﹣4.则min(﹣x2+3,﹣2x}的最大值是( )
A.3 B.2 C.1 D.0
5.对于二次函数y=﹣2x2+mx﹣1,当x<1时,y随x的增大而增大,则满足条件的m的取值范围是( )
A.m≥4 B.m≥3 C.m≥2 D.m≥﹣4
6.已知抛物线和直线交于,两点,其中,且满足,则直线一定经过( )
A.第一、二象限 B.第二、三象限
C.第三、四象限 D.第一、四象限
二、填空题
7.已知二次函数,当时,的最大值为9,则的值为 .
8.已知二次函敞.
(1)若点在该函数图象上,则的值为 .
(2)若点都在该函数图象上,且,则的取值范围为 .
9.已知,为x轴上两点,,为二次函数图象上两点,当时,二次函数y随x增大而减小,若,时,恒成立,则A、B两点的最大距离为 .
三、解答题
10.如图,直线分别交轴、轴于点,,抛物线经过点.
(1)求点的坐标和抛物线的函数表达式;
(2)若抛物线向左平移个单位后经过点,求的值.
11.已知二次函数的图象经过原点O和点,其中.
(1)当时
①求y关于x的函数表达式,并求出当x为何值时,y有最大值,最大值为多少?
②当和时(),函数值相等,求m,n之间的关系式.
(2)当时,在范围内,y是否存在最大值18?若存在,求出相应的t和x的值,若不存在,请说明理由.
12.在平面直角坐标系中,抛物线为常数,且经过和两点.
(1)求和的值用含的代数式表示;
(2)若该抛物线开口向下,且经过,两点,当时,随的增大而减小,求的取值范围;
(3)已知点,,若该抛物线与线段恰有一个公共点时,结合函数图象,求的取值范围.
13.顶点为的二次函数满足以下三个条件的任意两个:
其与轴的交点为;
其与轴的交点为和;
该函数其最大值为.
(1)从以上条件任选两个,求出函数的表达式;
(2)若存在直线,二次函数上的存在一个点,使得等于到直线的距离,求出点的坐标.
14. 图1是即将建造的“碗形”景观池的模拟图,设计师将它的外轮廓设计成如图2所示的
图形.它是由线段AC,线段BD,曲线AB,曲线CD围成的封闭图形,且AC//BD,BD在x轴上,曲线AB与曲线CD关于y轴对称.已知曲线CD是以C为顶点的抛物线的一部分,其函数解析式为:(p 为常数,8≤p≤40).
(1)当p=10时,求曲线AB的函数解析式.
(2)如图3,用三段塑料管EF,FG,EH围成一个一边靠岸的矩形荷花种植区,E,F分别在曲线CD,曲线AB上,G,H在x轴上.
①记EF=70米时所需的塑料管总长度为L1,EF=60米时所需的塑料管总长度为L2.若L1
15.已知二次函数.
(1)若它的图象经过点,求该函数的对称轴.
(2)若时,y的最小值为1,求出t的值.
(3)如果,两点都在这个二次函数的图象上,直线与该二次函数交于,两点,则是否为定值?若是,请求出该定值:若不是,请说明理由.
16.在二次函数中(),
(1)当时,
①求该二次函数图象的顶点坐标;
②当时,求y的取值范围;
(2)若,两点都在这个二次函数的图象上,且,求a的取值范围.
答案解析部分
1.【答案】B
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】A
6.【答案】B
7.【答案】
8.【答案】(1)2或-2
(2)-3<b<-2或b>2
9.【答案】8
10.【答案】(1)解:由可知,令,则,
∴点的坐标为,
令,则,
∴点坐标为,
代入抛物线的表达式,得,解得,
∴抛物线的函数表达式为;
(2)解:由(1)得,
∴平移后的抛物线为,将点代入,得,
解得,.
11.【答案】(1)解:当时,,
把、代入得,
,
∴,
∴二次函数为,
∵,
∴当时,有最大值,最大值为;
∵和时,函数值相等,
∴,
整理得,,
∵,则,
∴,
∴.
(2)解:∵二次函数的图象经过原点,
∴,
∴二次函数,
∴对称轴为直线,
∵二次函数的图象经过原点和点,
∴,
当时,对称轴,
∵,
∴时,有最大值,
即,
整理得,,
∴或,
∵
∴,
∴或不合,舍去;
当时,对称轴,
∵,
∴在对称轴的左侧,的值随的增大而增大,
∵,
∴当时,有最大值,
即,
解得,
∴,
∴;
综上,,.
12.【答案】(1)解:把和代入,
得:,
解得:
(2)解:抛物线经过,两点,
抛物线的对称轴为:直线,
抛物线开口向下,当时,随的增大而减小,
,即
(3)解:∵,
∴抛物线为:.
当时,如图,
抛物线与线段只有一个交点,根据抛物线的图象可知,抛物线不经过点N.
故时,,即,
解得:.
当时,若抛物线的顶点在线段上时,则,
解得:,,
当时,,
此时,顶点横坐标满足,符合题意;
∴当时,如图,抛物线与线段只有一个交点,
如图,
当时,.
此时顶点横坐标不满足,不符合题意,舍去;
若抛物线与线段有两个交点,且其中一个交点恰好为点 时,如图④:
把代入,得:
,
解得:,
故当x=2时,y>5,则抛物线不经过点N,和线段有1个交点,
解,
得.
综上所述:的取值范围为:或或时. 抛物线与线段恰有一个公共点.
13.【答案】(1)解:选择条件和,
二次函数与轴的交点为,
,
二次函数与轴的交点为和,
将点和代入函数,
,,
函数的表达式,
答:函数的表达式为:
(2)解:设点的坐标为,
点为函数的顶点,
点的坐标为,
直线,
点到直线的距离,
,
设,
到直线的距离等于,
,
,
或,
点或,
答:点的坐标为:或
14.【答案】(1)解:当p=10时,抛物线CD的解析式为:,
故C坐标为(10,40),
由对称得点A坐标为(-10,40),
∴抛物线AB的解析式为:.
(2)解:①根据题意,设E1(35,y1),E2(30,y2),
∵L1<L2,
∴35+y1<30+y2,
即:,
化简得:65-2p>20,
∴,
∴.
②解:设EF AC=2d,三段塑料管总长度为L,
根据题意可得:,
∴,
化简得:,
当d=10时,L有最大值110.
∴当EF与AC的差为20m时,三段塑料管总长度最大,最大值为110m.
15.【答案】(1)解:将点代入二次函数,得
,
解得:,
对称轴直线为:
;
(2)解:当时,,
∵抛物线开口向下,对称轴为直线,
∴当时,有最大值,
∵时,的最小值为1,
∴当时,,
解得:;
(3)解:是定值,理由:
∵,两点都在这个二次函数的图象上,
,
令,整理得:
,
∵直线与该二次函数交于,两点,
∴是方程的两个根,
是定值.
16.【答案】(1)解:①把代入得,
∴抛物线的顶点坐标为;
②∵当时,y随x的增大而增大,当时.y随x的增大而减小,
∴当时,y有最大值2.
∵当时,;当时,,
∴当时,;
(2)解:抛物线的对称轴为直线,
①当,即时,点B到对称轴的距离小于点A到对称轴的距离,
∴,解得,∴;
②当,即时,点B到对称轴的距离小于点A到对称轴的距离,
∴成立,∴,
③对称轴在点A左侧不合题意,舍去;
综上所述,.
试题分析部分
1、试卷总体分布分析
总分:98分
分值分布 客观题(占比) 14.0(14.3%)
主观题(占比) 84.0(85.7%)
题量分布 客观题(占比) 7(43.8%)
主观题(占比) 9(56.3%)
2、试卷题量分布分析
大题题型 题目量(占比) 分值(占比)
选择题 6(37.5%) 12.0(12.2%)
填空题 3(18.8%) 6.0(6.1%)
解答题 7(43.8%) 80.0(81.6%)
3、试卷难度结构分析
序号 难易度 占比
1 普通 (75.0%)
2 困难 (25.0%)
4、试卷知识点分析
序号 知识点(认知水平) 分值(占比) 对应题号
1 一次函数图象与坐标轴交点问题 10.0(10.2%) 10
2 二次函数图象的几何变换 12.0(12.2%) 1,10
3 二次函数图象上点的坐标特征 21.0(21.4%) 2,3,8,12
4 二次函数y=ax +bx+c的性质 35.0(35.7%) 2,3,5,8,9,15,16
5 换元法解一元二次方程 10.0(10.2%) 13
6 二次函数图象与系数的关系 17.0(17.3%) 6,12
7 点到直线的距离 10.0(10.2%) 13
8 二次函数的其他应用 10.0(10.2%) 14
9 二次函数y=ax +bx+c与二次函数y=a(x-h) +k的转化 2.0(2.0%) 1
10 二次函数的最值 16.0(16.3%) 4,7,9,11
11 二次函数与一次函数的综合应用 15.0(15.3%) 15
12 待定系数法求二次函数解析式 55.0(56.1%) 10,11,12,13,16
13 坐标系中的两点距离公式 10.0(10.2%) 13
14 二次函数图象与坐标轴的交点问题 2.0(2.0%) 2
1 / 1
同课章节目录
