2.3 等腰三角形的判定

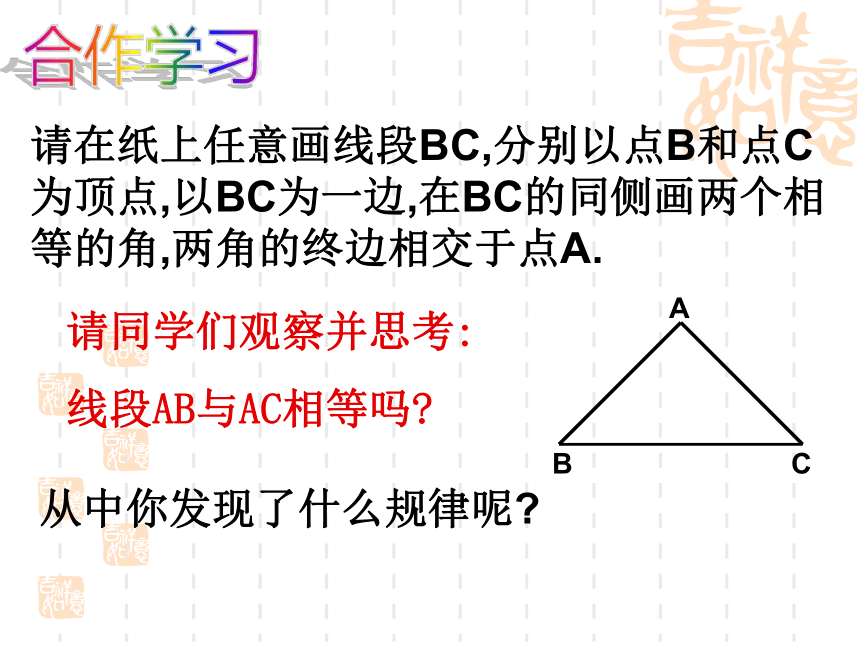
课件22张PPT。等腰三角形的判定如图所示,量出AC的长,就可知道河的宽度AB,你知道为什么吗?1.等腰三角形的定义?2.等腰三角形的性质?思考:根据等腰三角形的意义可知,如果一个三角形的两条边相等,那么就可判定这个三角形是等腰三角形.除此之外,还有其他的判定方法吗?知识回顾有两条边相等的三角形叫等腰三角形。2.等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合(等腰三角形三线合一).1.等腰三角形的两个底角相等(在同一个三角形中，等边对等角).合作学习请在纸上任意画线段BC,分别以点B和点C为顶点,以BC为一边,在BC的同侧画两个相等的角,两角的终边相交于点A.请同学们观察并思考:
线段AB与AC相等吗?从中你发现了什么规律呢?BCA如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
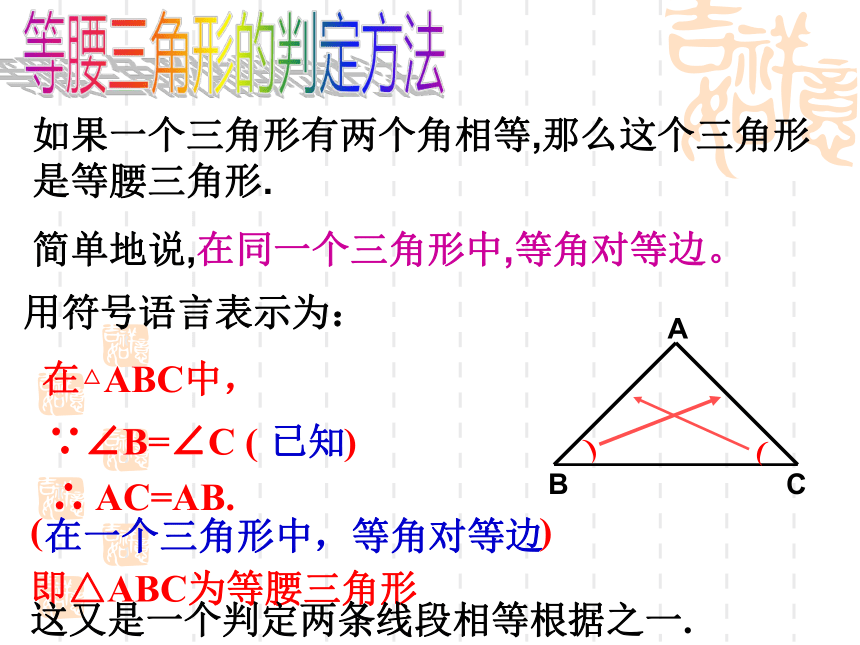
简单地说,在同一个三角形中,等角对等边。等腰三角形的判定方法已知在一个三角形中，等角对等边 在△ABC中， ∵∠B=∠C ( ) ∴ AC=AB. ( )
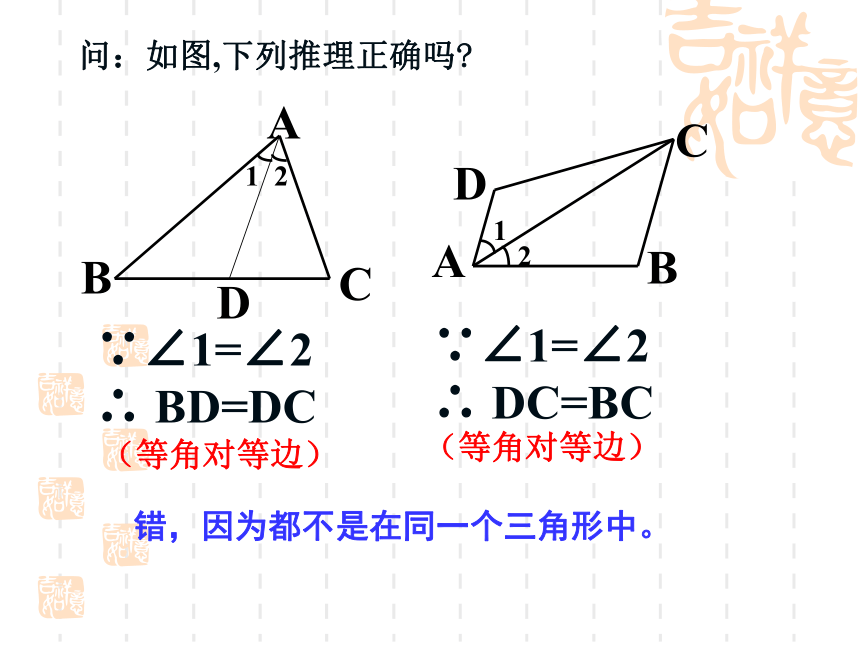
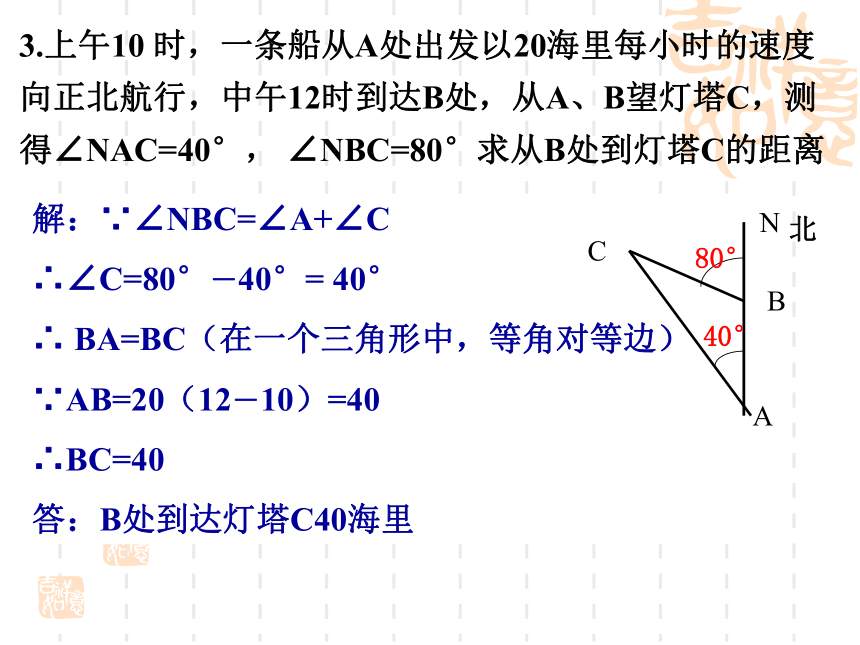
即△ABC为等腰三角形用符号语言表示为：这又是一个判定两条线段相等根据之一.((在△ABC中, ∠B=∠C,则△ABC是等腰三角形.在△ABD与△ACD∠1=∠2∴ △ABD ≌ △ACD ∠B=∠CAD=AD∴AB=AC(全等三角形的对应边相等)∴ △ ABC是等腰三角形还有什么方法可证明? 问：如图,下列推理正确吗? （等角对等边）（等角对等边）错，因为都不是在同一个三角形中。B例1 一次数学实践活动的内容是测量河宽.如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°.量出AC的长,它就是河的宽度(即A,B之间的距离).这个方法正确吗?请说明理由.∵∠DAC=∠B+∠C（三角形外角的性质）∴ ∠ABC=∠DAC－∠C=60°－ 30°= 30°解：小聪的测量方法正确，理由如下：∴ ∠ABC= ∠C ∴ AB= AC 想一想：你还有其他的测量方法吗？反馈练习 1.在△ABC中, 已知∠A=50°，∠B=65°，判断△ABC是什么三角形，为什么?△ABC是等腰三角形, 因为∠B=65°, ∠A=50°, 所以∠C=65°, ∠B =∠C=65°2.如图，已知∠A=36°，∠DBC=36°，∠C=72°，则∠1=_____，∠2=_____，图中的等腰三角形有________________.36°72°△ABC△DBA△BCD解：∵∠NBC=∠A+∠C
∴∠C=80°－40°= 40°
∴ BA=BC（在一个三角形中，等角对等边）
∵AB=20（12－10）=40
∴BC=40
答：B处到达灯塔C40海里3.上午10 时，一条船从A处出发以20海里每小时的速度向正北航行，中午12时到达B处，从A、B望灯塔C，测得∠NAC=40°， ∠NBC=80°求从B处到灯塔C的距离例2 如图，BD是等腰三角形ABC的底边AC上的高，DE∥BC，交AB于点E，判断△BED是不是等腰三角形，并说明理由.(1)要说明△BDE是等腰三角形，需要说明哪两条边相等, 还是两个角等？(2)要说明BE=DE,应说明哪两角相等？BE=DE∠EBD=∠EDB(4) 由∠EBD=∠CBD 能转化为∠EBD=∠EDB吗？(3) 由BD是等腰三角形ABC的底边AC上的高，你能得到什么结论？∠EBD=∠CBD或∠EBD=∠EDBDE‖BC课内练习解:(两直线平行,同位角相等)(在同一个三角形中,等角对等边)∵ DE∥BC1. 如图，在△ABC中，D、E分别是AB、AC上的点，DE∥BC，∠1= ∠2。说明△ABC的等腰三角形的理由.2. 如图，在△ABC中，D、E分别是AC、AB上的点，BD、CE交于点O。若∠BEO= ∠CDO，BE=CD。问△ABC是等腰三角形吗？请说明理由.小小设计家: 在下图三角形的边上找出一点，使得该点与
三角形的两顶点构成等腰三角形！BAC50°110°20°小小设计家:1、对∠A进行讨论2、对∠B进行讨论3、对∠C进行讨论（分类讨论）在同一个三角形中,等角对等边.本节课我们学习了什么内容？课堂小结有两边相等的三角形是等腰三角形2.等边对等角3. 三线合一4.是轴对称图形2.等角对等边1.两边相等1.两腰相等1.如果三角形一个角的外的角平分线平行于三角形的第三边，那么这个三角形是等腰三角形吗？为什么？3.如图，△ABC中，AB=AC，∠B=∠C，BD=CE，说明∠1=∠2的理由。拓展提高通过以上的解答大家发现当哪个角的度数为定值时, ∠CDE为定值.1.如图，AB=AC，D是BC上一点，AD=AE，∠BAD=40°，求∠CDE的度数。2.如图，GF⊥AF于F，且AB=BC=CD=DE=EF=FG，求∠A的度数。3.如图，△ABC中，AB=AC，直线DE交AB、BC于D、F，交AC延长线于E。若DF=EF，说明BD=CE的理由。1. 如图1，在△ABC中，已知∠ABC=∠ACB，BG平分∠ABC，CG平分∠ACB。（1）由以上条件，你能得到什么结论？并说明理由。（2）如图2，添加EF∥BC，你又能得到什么结论？并说明理由。