2.5 直角三角形

课件13张PPT。2.5 直角三角形(2)复习上节课学习的直角三角形知识:∟１．直角三角形的两个锐角互余．(性质）
２．有两个角互余的三角形是直角三角形（判定）
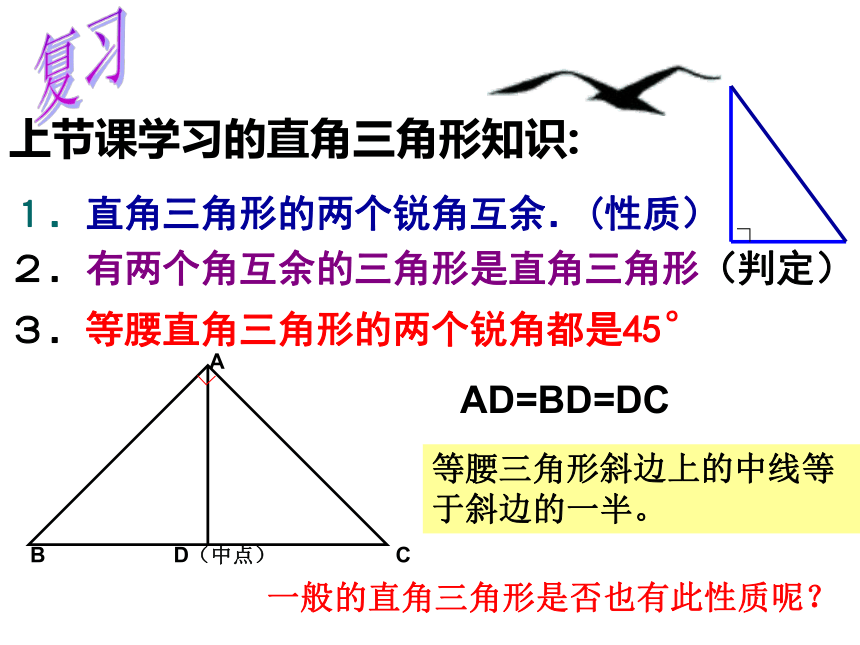
３．等腰直角三角形的两个锐角都是45°ABCD（中点）∟AD=BD=DC等腰三角形斜边上的中线等于斜边的一半。一般的直角三角形是否也有此性质呢？任意画一个直角三角形，作出斜边上的中线，并利用圆规比较中线与斜边的一半的长短．你发现了什么？
（请所有同学把结果都说出来．）操作实践，总结规律:ＢＡＣＤ总结：直角三角形一个特殊性质：★直角三角形斜边上的中线
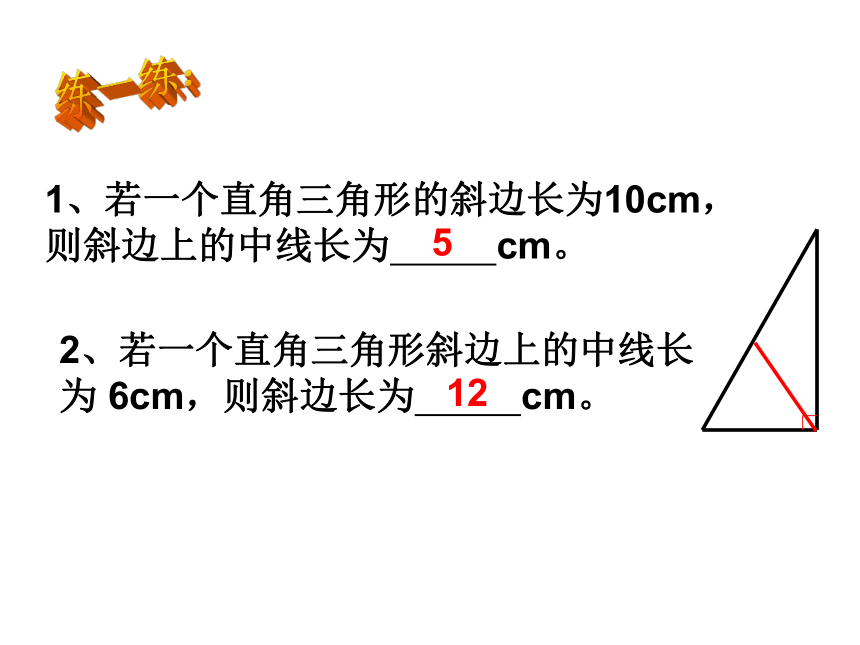
等于斜边的一半几何语言格式：练一练：1、若一个直角三角形的斜边长为10cm，则斜边上的中线长为 cm。52、若一个直角三角形斜边上的中线长为 6cm，则斜边长为 cm。12 ★直角三角形斜边上的中线
等于斜边的一半。直角三角形一个特殊性质：反过来，若三角形一边上的中线等于这边的一半，则这个三角形是直角三角形吗？★若三角形一边上的中线等于这边的一半，
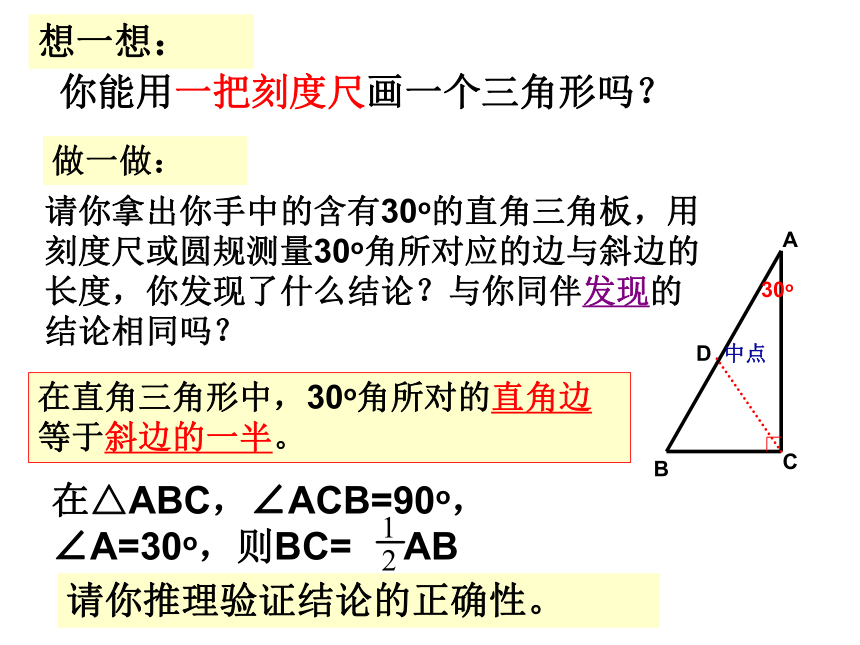
则这个三角形是直角三角形。试说明理由?想一想：你能用一把刻度尺画一个三角形吗？做一做：请你拿出你手中的含有30o的直角三角板，用刻度尺或圆规测量30o角所对应的边与斜边的长度，你发现了什么结论？与你同伴发现的结论相同吗？在直角三角形中，30o角所对的直角边等于斜边的一半。请你推理验证结论的正确性。D 中点1、已知，在Rt△ABC中，∠A=90o，∠B=30o，BC=6cm，则AC= cm练一练2、若等腰三角形的底角等于15o，腰长20，则腰上的高等于 。3∟10 例3、一名滑雪运动员沿着倾斜角为30°的斜坡，从A滑行至B。已知AB＝200m，问这名滑雪运动员的高度下降了多少m？30°AB解：如图，作Rt△ABC的斜边上的中线CD，则CD=AD=0.5AB=0.5×200=100(m)（直角三角形斜边上的中线等于斜边的一半）∵∠B=300∴∠A=900－∠B=900－300=600(直角三角形的两个锐角互余)∴△ADC是等边三角形(有一个角是60°的等腰三角形是等边三角形)∴AC=AD=100(m)答:这名滑雪运动员的高度下降了100m.30°AB练习如图，已知AD⊥BD，AC⊥BC，E为AB的中点，试判断DE与CE是否相等，并说明理由。说明两条线段相等，有时还可以通过第三条线段进行等量代换。如图，AD是△ABC的角平分线，过点B向AD的延长线作垂线BE，垂足为E，F是AB的中点，则EF∥AC。试说明理由。迁移拓展直角三角形的性质小结　１．直角三角形的两个锐角互余．
　２．有两个角互余的三角形是直角三角形．
　３．等腰直角三角形的两个锐角都是45°４．直角三角形斜边上的中线等于斜边的一半．5.在直角三角形中，30o角所对的直角边等于斜边的一半。课本　第３７页
　　　第２、３．
作业本（2）作业