浙教版数学八年级上册2.3等腰三角形的判定定理 精品同步练习(含解析)
文档属性
| 名称 | 浙教版数学八年级上册2.3等腰三角形的判定定理 精品同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-19 14:22:35 | ||
图片预览



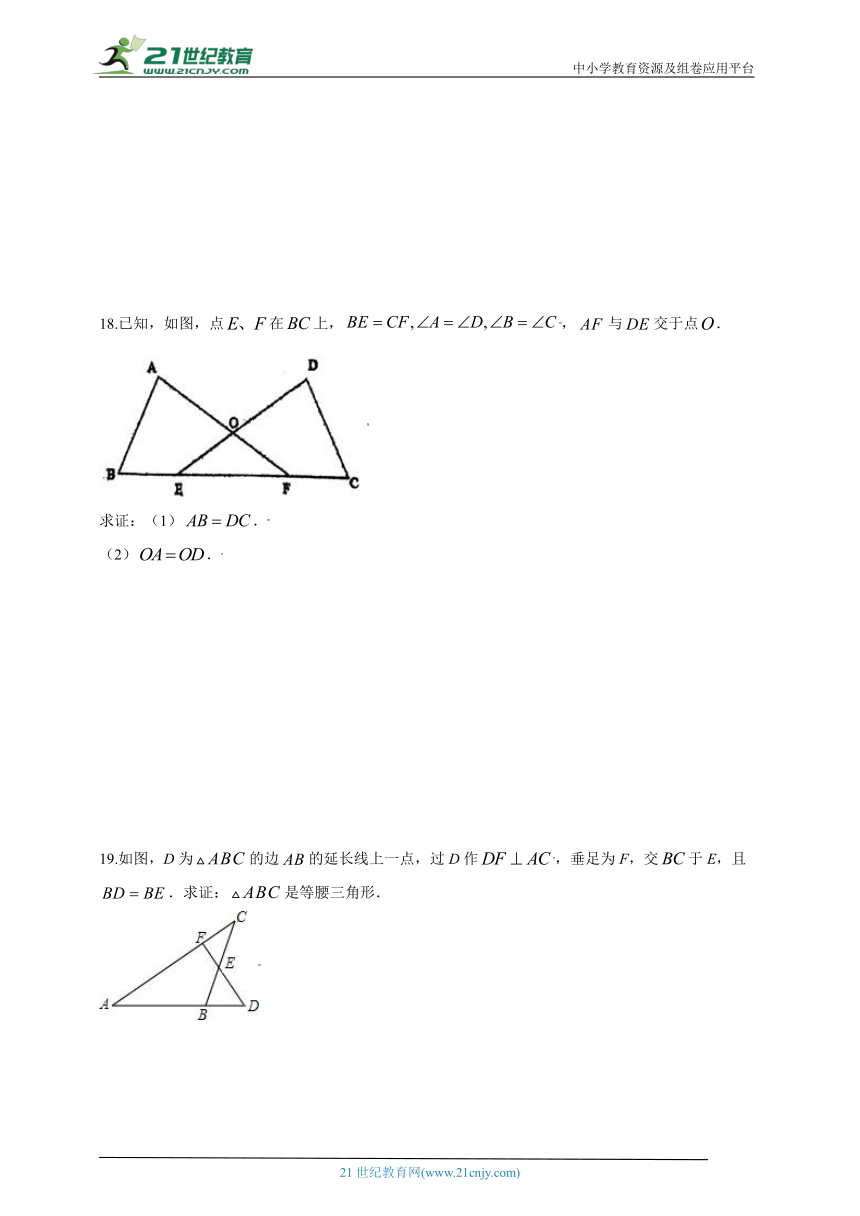
文档简介
中小学教育资源及组卷应用平台
浙教版八年级上册数学 2.3等腰三角形的判定定理 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.等腰三角形的一边等于3,一边等于6,则它的周长为( )
A.12 B.12或15 C.15或18 D.15
2..若等腰三角形有一个角为40°,则它的顶角为( )
A.40° B.100° C.40°或100° D.无法确定
3.△ABC中,AD,BE分别是边BC,AC上的高,若∠EBC=∠BAD,则△ABC一定是( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
4.在平面直角坐标系中,已知点A(3,3),在x轴的正半轴上确定一点P,使得三角形AOP是等腰三角形,则符合条件的点P共有( )
A.2 个 B.3个 C.4个 D.1个
5.列说法错误的是( )
A.有两个角相等的三角形是等腰三角形
B.到线段两端的距离相等的点,在线段的垂直平分线上
C.成轴对称的两个图形中,对称轴垂直平分连结两个对称点的线段
D.面积相等的两个三角形全等
6.如图,已知每个小方格的边长为1,A,B,两点都在小方格的顶点上,请在图形中找一个格点C,使是等腰三角形,这样的格点C有( )
A.5个 B.6个 C.7个 D.8个
7.如图,关于△ABC,给出下列四组条件:
①△ABC中,AB=AC;
②△ABC中,∠B=56°,∠BAC=68°;
③△ABC中,AD⊥BC,AD平分∠BAC;
④△ABC中,AD⊥BC,AD平分边BC.
其中,能判定△ABC是等腰三角形的条件共有( )
A.1组 B.2组 C.3组 D.4组
8.已知∠MON=20° ,点A B分别是射线OM、ON上的动点(A、B不与点0重合),若ABOM,在射线ON上有一点C,设∠OAC=x°,下列x的值不能使△ABC为等腰三角形的是( )
A.20
B.45
C.50
D.125
9.如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+∠C;
②AE+BF=EF;
③当∠C=90°时,E,F分别是AC,BC的中点;
④若OD=a,CE+CF=2b,则S△CEF=ab.
其中正确的是( )
A.①② B.③④ C.①②④ D.①③④
10..如图,△ABC,点D在AC上,连接BD,∠ABD=2∠DBC,∠ADB=2∠C,∠DBC=∠A,则图中共有等腰三角形( )个.
A.0 B.1 C.2 D.3
填空题(本大题共5小题,每小题4分,共20分。)
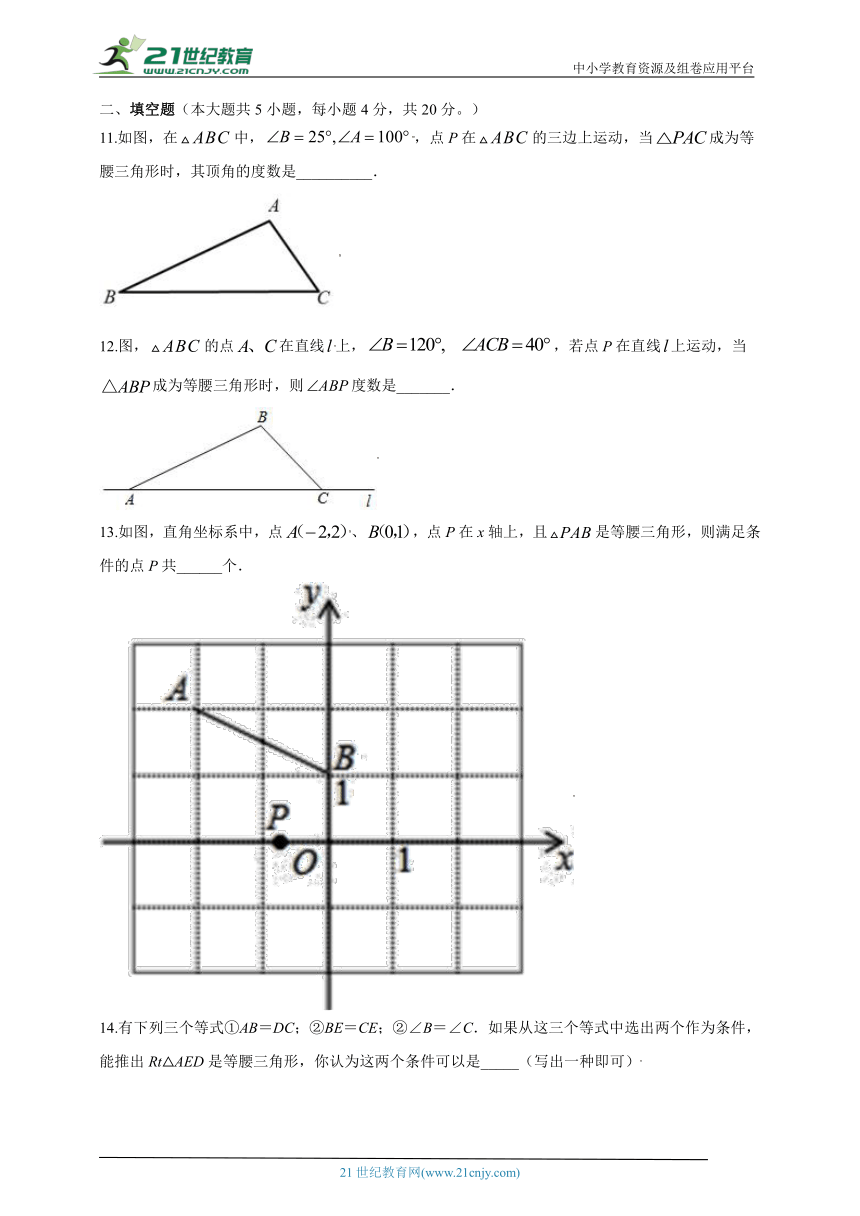
11.如图,在中,,点P在的三边上运动,当成为等腰三角形时,其顶角的度数是__________.
12.图,的点在直线上,,若点P在直线上运动,当成为等腰三角形时,则度数是_______.
13.如图,直角坐标系中,点、,点P在x轴上,且是等腰三角形,则满足条件的点P共______个.
14.有下列三个等式①AB=DC;②BE=CE;②∠B=∠C.如果从这三个等式中选出两个作为条件,能推出Rt△AED是等腰三角形,你认为这两个条件可以是_____(写出一种即可)
15.已知在中,且为最小的内角,过顶点B的一条直线把这个三角形分割成两个等腰三角形,则_______
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,点E是AB的中点,连结DE.
(1)求证:△ABD是等腰三角形;
(2)求∠BDE的度数.
17.(1)如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于点E、F,试猜想EF、BE、CF之间有怎样的关系,并说明理由;
(2)如图,若将图①中∠ACB的平分线改为外角∠ACD的平分线,其它条件不变,请直接写出EF、BE、CF之间的关系 .
18.已知,如图,点在上,,与交于点.
求证:(1).
(2).
19.如图,D为的边的延长线上一点,过D作,垂足为F,交于E,且.求证:是等腰三角形.
20.已知:如图,△ABC中,AC=BC,D、E分别为AB,AC上的点.若AD=AE,DF=BD,试求∠BDF的度数.
参考答案
选择题
1.【答案】D
【分析】分别从若腰长为3,底边长为6,若腰长为6,底边长为3,去分析求解即可求得答案,注意三角形的三边关系.
【详解】解:①若腰长为3,底边长为6,
∵3+3=6,
∴不能组成三角形,舍去;
②若腰长为6,底边长为3,
则它的周长是:6+6+3=15.
∴它的周长是15,
故选:D.
2.【答案】C
【分析】三角形内角与相邻的的外角和为180°,三角形内角和为180°,等腰三角形两底角相等,然后分别讨论40°为顶角时和40°为底角时,然后即可求得答案.
【详解】当40°是等腰三角形的顶角时,则顶角就是40°;
当40°是等腰三角形的底角时,则顶角是180°-40°×2=100°,故选C.
3.【分析】发现∠ABC与∠C分别是∠BAD与∠EBC的余角,得到二角相等,根据等腰三角形的判定可得答案.
【解析】∵∠EBC+∠C=90°,∠C+∠CAD=90°,
∴∠CAD=∠EBC,
∵∠EBC=∠BAD
∴∠BAD=∠CAD,∠CAD+∠C=90°∠BAD+∠ABC=90°
∴∠ABC=∠C
∴AB=AC
∴△ABC为等腰三角形.
故选:A.
4.【分析】分别从当OP=AP时、当OA=OP时、当OA=AP时去分析求解即可求得答案.
【解析】如图所示,当OP=AP时,P1(3,0),
当OA=OP时,OP=OA=3,此时P1(3,0),
当OA=AP时,P3(6,0).
故符合条件的点P共有3个.
故选:B.
5.【答案】D
【分析】A.根据等腰三角形的判定进行判断即可;B.根据线段垂直平分线的判定进行判断即可;B.根据轴对称的性质进行判断即可;D.根据全等三角形的判定进行判断即可.
【详解】A.根据等腰三角形的判定可知:有两个角相等的三角形是等腰三角形,故A正确;
B.根据线段垂直平分线的判定定理可知:到线段两端的距离相等的点在线段的垂直平分线上,故B正确;
C.根据轴对称的性质可知:成轴对称的两个图形,对称轴垂直平分连结两个对称点的线段,故C正确;
D.根据三角形的面积公式可知:面积相等的两个三角形不一定全等,故D错误.
故选:D.
6.【答案】D
【分析】分AB为腰和为底两种情况考虑,画出图形,即可找出点C的个数.
【详解】解:当AB为腰时,分别以A、B点为顶点,以AB为半径作圆,可找出格点点C的个数有6个;
当AB为底时,作AB的垂直平分线,可找出格点C的个数有2个,
6+2=8.
故选:D.
7.【答案】D
【分析】根据等腰三角形的判定定理即可逐一判断.
【详解】解:①∵△ABC中,AB=AC,
∴△ABC是等腰三角形,故①正确;
②∵△ABC中,∠B=56°,∠BAC=68°,
∴∠C=180°﹣∠BAC﹣∠B=180°﹣68°﹣56°=56°,
∴∠B=∠C,则AB=AC,
∴△ABC是等腰三角形,故②正确;
③∵△ABC中,AD⊥BC,AD平分∠BAC,
∴∠BAD=∠CAD,∠ADB=∠ADC,
∵∠B+∠BAD+∠ADB=180°,∠C+∠CAD+∠ADC=180°,
∴∠B=∠C,则AB=AC,
∴△ABC是等腰三角形,故③正确;
④∵△ABC中,AD⊥BC,AD平分边BC,
∴AB=AC,
∴△ABC是等腰三角形,故④正确;
即正确的个数是4,
故选:D.
8.【答案】B
【分析】依据题意作出图形,按照选项画出C的位置,根据等腰三角形的判定进行判断.
【详解】A.当∠OAC=20°时,如图所示,
∠ACB=∠MON+∠OAC=40°,∠BAC=90°-∠OAC=70°,
∴∠ABC=180°-40°-70°=70°,
∴∠BAC=∠ABC
∴△ABC是等腰三角形,故A不符合题意;
B. 当∠OAC=45°时,如图所示,
∠ACB=∠MON+∠OAC=65°,∠BAC=90°-∠OAC=45°,∠ABC=70°,
∴△ABC不是等腰三角形,故B符合题意;
C. 当∠OAC=50°时,如图所示,
∠ACB=∠MON+∠OAC=70°,∠BAC=20°,∠ABC=70°,
∴∠ACB=∠ABC
∴△ABC是等腰三角形,故C不符合题意;
D. 当∠OAC=125°时,如图所示,
∠BAC=∠OAC-90°=35°,∠ABC=∠BAC+∠BCA=70°,
∴∠BAC=∠BCA=35°,
∴△ABC是等腰三角形,故D不符合题意;
故选B.
9.【答案】C
【分析】根据角平分线的定义和三角形内角和定理判断①;根据角平分线的定义和平行线的性质判断②;根据三角形三边关系判断③;根据角平分线的性质判断④.
【详解】∵∠BAC和∠ABC的平分线相交于点O,
∴∠OBA=∠CBA,∠OAB=∠CAB,
∴∠AOB=180°﹣∠OBA﹣∠OAB
=180°﹣∠CBA﹣∠CAB
=180°﹣(180°﹣∠C)
=90°+∠C,①正确;
∵EF∥AB,
∴∠FOB=∠ABO,又∠ABO=∠FBO,
∴∠FOB=∠FBO,
∴FO=FB,
同理EO=EA,
∴AE+BF=EF,②正确;
当∠C=90°时,AE+BF=EF<CF+CE,
∴E,F不是AC,BC的中点,③错误;
作OH⊥AC于H,
∵∠BAC和∠ABC的平分线相交于点O,
∴点O在∠C的平分线上,
∴OD=OH,
∴S△CEF=×CF×OD×CE×OH=ab,④正确.
故选C.
10.【答案】D
【分析】根据等腰三角形的判定分别证出DB=DC,AB=AD,AB=CB即可.
【解答】解:图中共有等腰三角形3个,理由如下:
∵∠ADB=∠C+∠DBC,∠ADB=2∠C,
∴∠DBC=∠C,
∴△BCD是等腰三角形,DB=DC,
∵∠ABD=2∠DBC,
∴∠ABD=∠ADB,
∴△ABD是等腰三角形,AB=AD,
∵∠DBC=∠A,
∴∠A=∠C,
∴△ABC是等腰三角形,AB=CB,
故选:D.
填空题
11.【答案】100°或55°或70°
【分析】作出图形,然后分点P在AB上与BC上两种情况讨论求解.
【详解】解:①如图1,点P在AB上时,AP=AC,顶角为∠A=100°,
②∵∠ABC=25°,∠BAC=100°,
∴∠ACB=180°-25°-100°=55°,
如图2,点P在BC上时,若AC=PC,顶角为∠ACB=55°,
如图3,若AC=AP,则顶角为∠CAP=180°-2∠ACB=180°-2×55°=70°,
综上所述,顶角为105°或55°或70°.
故答案为:100°或55°或70°.
12.【答案】10°或80°或20°或140°
【分析】分三种情形:,,分别求解即可解决问题.
【详解】解:如图,
在中,,
①当时,,,
②当时,,
③当时,,
综上所述,满足条件的的值为或或或.
13.【答案】4
【分析】分AB=AP、BA=BP、PA=PB三种情况,画出图形即可得答案.
【详解】①AB=AP:以A为圆心,AB长为半径画弧,与x轴有2个交点P1、P2,
∴P1、P2,符号条件,
②BA=BP:以B为圆心,BA长为半径画弧,与x轴有2个交点P3、点(2,0),
∵点(2,0)与AB不能构成三角形,
∴P3符合条件,
③PA=PB:作线段AB的垂直平分线,与x轴有1个交点P4,
∴P4A=P4B,
∴P4符合条件,
综上所述,符合条件的点共有4个.
故答案为:4.
14.【答案】①②或①③或②③.(答案不唯一)
【分析】依据条件判定△ABE≌△DCE,即可得到AE=DE,进而得出Rt△AED是等腰三角形.
【详解】解:当AB=DC,BE=CE,∠AEB=∠DEC时,Rt△ABE≌Rt△DCE(HL),故AE=DE,即Rt△AED是等腰三角形;
当AB=DC,∠B=∠C,∠AEB=∠DEC时,△ABE≌△DCE(AAS),故AE=DE,即Rt△AED是等腰三角形;
当BE=CE,∠B=∠C,∠AEB=∠DEC时,△ABE≌△DCE(ASA),故AE=DE,即Rt△AED是等腰三角形.
故答案为:①②或①③或②③.(答案不唯一)
15.【答案】123°或132°或90°或48°
【分析】根据题意作图,结合等腰三角形的性质分情况讨论即可求解.
【详解】解:如图,若BC=CD,AD=BD,
由题意可得:∠DBC=∠BDC=(180°-∠C)÷2=82°,
∴∠ABD=∠BAD=∠BDC=41°,
∴∠ABC=∠ABD+∠DBC=123°,
∵∠ADB=180°-82°=98°,
则在BC=CD的前提下只有AD=BD;
如图,若CD=BD,AB=BD,
由题意可得:∠DBC=∠C=16°,
∴∠ADB=2∠C=32°,
∴∠A=∠ADB=32°,
∠ABD=180°-∠A-∠ADB=116°,
∴∠ABC=∠ABD+∠DBC=132°,
符合最小的内角为∠C=16°,
如图,若BD=CD,AB=AD,
则∠C=∠DBC=16°,
∴∠ADB=∠ABD=2∠C=32°,
∴∠A=180°-2×32°=116°,
∴∠ABC=∠ABD+∠DBC=48°;
如图,若BD=CD,AD=BD,
∴∠ADB=2∠C=2∠DBC=32°,
∴∠A=∠ABD=(180°-32°)÷2=74°,
∴∠ABC=∠ABD+∠DBC=90°;
若BD=BC,
则∠C=∠CDB=16°,
∴∠ADB=180°-∠CDB=164°,
则只能满足AD=BD,
∴∠A=∠CDB=8°,
即∠A<∠C,不满足;
综上:∠ABC的度数为123°或132°或90°或48°.
故答案为:123°或132°或90°或48°.
解答题
16.【解答】证明:(1)∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=36°,∠A=36°,
∴BD=AD,
即△ABD是等腰三角形;
(2)∵点E是AB的中点,
∴AE=EB,
∴∠DEB=90°,
∴∠BDE=90°﹣36°=54°.
17.【解析】(1)EF=BE+CF,
理由:∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=∠OBC,∠FCO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF;
(2)不成立,
理由:∵BO平分∠ABC,CO平分∠ACD,
∴∠EBO=∠OBC,∠FCO=∠OCD,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCD,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴EF=OE﹣OF=BE﹣CF.
故答案为EF=BE﹣CF.
18.【答案】(1)见解析;(2)见解析
【分析】(1)只要证明△ABF≌△DCE(AAS)即可;
(2)只要证明AF=DE,OF=OE即可;
【详解】证明:(1)∵BE=CF,
∴BF=CE,
∵在△ABF和△DCE中
,
∴△ABF≌△DCE(AAS),
∴AB=DC;
(2)∵△ABF≌△DCE,
∴∠AFB=∠DEC,AF=DE,
∴OE=OF,
∴AF-OF=DE-OE,
∴.
19.【详解】解:证明:∵BD=BE,
∴∠BDE=∠BED
又∵∠BED=∠CEF,
∴∠BDE=∠CEF
又∵DF⊥AC,
∴∠A+∠BDF=90°,∠C+∠CEF=90°,
∴∠A=∠C,
∴AB=BC(等角对等边),
∴△ABC是等腰三角形.
20.【解答】解:∵CA=CB,
∴设∠A=∠B=x.
∵DF=DB,
∴∠B=∠F=x,
∵AD=AE,
∴∠ADE=∠AED=∠B+∠F=2x.
在△AED中,x+2x+2x=180°,
∴x=36°,
∴∠B=∠F=36°,
∴∠BDF=180°﹣2×36°=108°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版八年级上册数学 2.3等腰三角形的判定定理 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.等腰三角形的一边等于3,一边等于6,则它的周长为( )
A.12 B.12或15 C.15或18 D.15
2..若等腰三角形有一个角为40°,则它的顶角为( )
A.40° B.100° C.40°或100° D.无法确定
3.△ABC中,AD,BE分别是边BC,AC上的高,若∠EBC=∠BAD,则△ABC一定是( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
4.在平面直角坐标系中,已知点A(3,3),在x轴的正半轴上确定一点P,使得三角形AOP是等腰三角形,则符合条件的点P共有( )
A.2 个 B.3个 C.4个 D.1个
5.列说法错误的是( )
A.有两个角相等的三角形是等腰三角形
B.到线段两端的距离相等的点,在线段的垂直平分线上
C.成轴对称的两个图形中,对称轴垂直平分连结两个对称点的线段
D.面积相等的两个三角形全等
6.如图,已知每个小方格的边长为1,A,B,两点都在小方格的顶点上,请在图形中找一个格点C,使是等腰三角形,这样的格点C有( )
A.5个 B.6个 C.7个 D.8个
7.如图,关于△ABC,给出下列四组条件:
①△ABC中,AB=AC;
②△ABC中,∠B=56°,∠BAC=68°;
③△ABC中,AD⊥BC,AD平分∠BAC;
④△ABC中,AD⊥BC,AD平分边BC.
其中,能判定△ABC是等腰三角形的条件共有( )
A.1组 B.2组 C.3组 D.4组
8.已知∠MON=20° ,点A B分别是射线OM、ON上的动点(A、B不与点0重合),若ABOM,在射线ON上有一点C,设∠OAC=x°,下列x的值不能使△ABC为等腰三角形的是( )
A.20
B.45
C.50
D.125
9.如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
①∠AOB=90°+∠C;
②AE+BF=EF;
③当∠C=90°时,E,F分别是AC,BC的中点;
④若OD=a,CE+CF=2b,则S△CEF=ab.
其中正确的是( )
A.①② B.③④ C.①②④ D.①③④
10..如图,△ABC,点D在AC上,连接BD,∠ABD=2∠DBC,∠ADB=2∠C,∠DBC=∠A,则图中共有等腰三角形( )个.
A.0 B.1 C.2 D.3
填空题(本大题共5小题,每小题4分,共20分。)
11.如图,在中,,点P在的三边上运动,当成为等腰三角形时,其顶角的度数是__________.
12.图,的点在直线上,,若点P在直线上运动,当成为等腰三角形时,则度数是_______.
13.如图,直角坐标系中,点、,点P在x轴上,且是等腰三角形,则满足条件的点P共______个.
14.有下列三个等式①AB=DC;②BE=CE;②∠B=∠C.如果从这三个等式中选出两个作为条件,能推出Rt△AED是等腰三角形,你认为这两个条件可以是_____(写出一种即可)
15.已知在中,且为最小的内角,过顶点B的一条直线把这个三角形分割成两个等腰三角形,则_______
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,点E是AB的中点,连结DE.
(1)求证:△ABD是等腰三角形;
(2)求∠BDE的度数.
17.(1)如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于点E、F,试猜想EF、BE、CF之间有怎样的关系,并说明理由;
(2)如图,若将图①中∠ACB的平分线改为外角∠ACD的平分线,其它条件不变,请直接写出EF、BE、CF之间的关系 .
18.已知,如图,点在上,,与交于点.
求证:(1).
(2).
19.如图,D为的边的延长线上一点,过D作,垂足为F,交于E,且.求证:是等腰三角形.
20.已知:如图,△ABC中,AC=BC,D、E分别为AB,AC上的点.若AD=AE,DF=BD,试求∠BDF的度数.
参考答案
选择题
1.【答案】D
【分析】分别从若腰长为3,底边长为6,若腰长为6,底边长为3,去分析求解即可求得答案,注意三角形的三边关系.
【详解】解:①若腰长为3,底边长为6,
∵3+3=6,
∴不能组成三角形,舍去;
②若腰长为6,底边长为3,
则它的周长是:6+6+3=15.
∴它的周长是15,
故选:D.
2.【答案】C
【分析】三角形内角与相邻的的外角和为180°,三角形内角和为180°,等腰三角形两底角相等,然后分别讨论40°为顶角时和40°为底角时,然后即可求得答案.
【详解】当40°是等腰三角形的顶角时,则顶角就是40°;
当40°是等腰三角形的底角时,则顶角是180°-40°×2=100°,故选C.
3.【分析】发现∠ABC与∠C分别是∠BAD与∠EBC的余角,得到二角相等,根据等腰三角形的判定可得答案.
【解析】∵∠EBC+∠C=90°,∠C+∠CAD=90°,
∴∠CAD=∠EBC,
∵∠EBC=∠BAD
∴∠BAD=∠CAD,∠CAD+∠C=90°∠BAD+∠ABC=90°
∴∠ABC=∠C
∴AB=AC
∴△ABC为等腰三角形.
故选:A.
4.【分析】分别从当OP=AP时、当OA=OP时、当OA=AP时去分析求解即可求得答案.
【解析】如图所示,当OP=AP时,P1(3,0),
当OA=OP时,OP=OA=3,此时P1(3,0),
当OA=AP时,P3(6,0).
故符合条件的点P共有3个.
故选:B.
5.【答案】D
【分析】A.根据等腰三角形的判定进行判断即可;B.根据线段垂直平分线的判定进行判断即可;B.根据轴对称的性质进行判断即可;D.根据全等三角形的判定进行判断即可.
【详解】A.根据等腰三角形的判定可知:有两个角相等的三角形是等腰三角形,故A正确;
B.根据线段垂直平分线的判定定理可知:到线段两端的距离相等的点在线段的垂直平分线上,故B正确;
C.根据轴对称的性质可知:成轴对称的两个图形,对称轴垂直平分连结两个对称点的线段,故C正确;
D.根据三角形的面积公式可知:面积相等的两个三角形不一定全等,故D错误.
故选:D.
6.【答案】D
【分析】分AB为腰和为底两种情况考虑,画出图形,即可找出点C的个数.
【详解】解:当AB为腰时,分别以A、B点为顶点,以AB为半径作圆,可找出格点点C的个数有6个;
当AB为底时,作AB的垂直平分线,可找出格点C的个数有2个,
6+2=8.
故选:D.
7.【答案】D
【分析】根据等腰三角形的判定定理即可逐一判断.
【详解】解:①∵△ABC中,AB=AC,
∴△ABC是等腰三角形,故①正确;
②∵△ABC中,∠B=56°,∠BAC=68°,
∴∠C=180°﹣∠BAC﹣∠B=180°﹣68°﹣56°=56°,
∴∠B=∠C,则AB=AC,
∴△ABC是等腰三角形,故②正确;
③∵△ABC中,AD⊥BC,AD平分∠BAC,
∴∠BAD=∠CAD,∠ADB=∠ADC,
∵∠B+∠BAD+∠ADB=180°,∠C+∠CAD+∠ADC=180°,
∴∠B=∠C,则AB=AC,
∴△ABC是等腰三角形,故③正确;
④∵△ABC中,AD⊥BC,AD平分边BC,
∴AB=AC,
∴△ABC是等腰三角形,故④正确;
即正确的个数是4,
故选:D.
8.【答案】B
【分析】依据题意作出图形,按照选项画出C的位置,根据等腰三角形的判定进行判断.
【详解】A.当∠OAC=20°时,如图所示,
∠ACB=∠MON+∠OAC=40°,∠BAC=90°-∠OAC=70°,
∴∠ABC=180°-40°-70°=70°,
∴∠BAC=∠ABC
∴△ABC是等腰三角形,故A不符合题意;
B. 当∠OAC=45°时,如图所示,
∠ACB=∠MON+∠OAC=65°,∠BAC=90°-∠OAC=45°,∠ABC=70°,
∴△ABC不是等腰三角形,故B符合题意;
C. 当∠OAC=50°时,如图所示,
∠ACB=∠MON+∠OAC=70°,∠BAC=20°,∠ABC=70°,
∴∠ACB=∠ABC
∴△ABC是等腰三角形,故C不符合题意;
D. 当∠OAC=125°时,如图所示,
∠BAC=∠OAC-90°=35°,∠ABC=∠BAC+∠BCA=70°,
∴∠BAC=∠BCA=35°,
∴△ABC是等腰三角形,故D不符合题意;
故选B.
9.【答案】C
【分析】根据角平分线的定义和三角形内角和定理判断①;根据角平分线的定义和平行线的性质判断②;根据三角形三边关系判断③;根据角平分线的性质判断④.
【详解】∵∠BAC和∠ABC的平分线相交于点O,
∴∠OBA=∠CBA,∠OAB=∠CAB,
∴∠AOB=180°﹣∠OBA﹣∠OAB
=180°﹣∠CBA﹣∠CAB
=180°﹣(180°﹣∠C)
=90°+∠C,①正确;
∵EF∥AB,
∴∠FOB=∠ABO,又∠ABO=∠FBO,
∴∠FOB=∠FBO,
∴FO=FB,
同理EO=EA,
∴AE+BF=EF,②正确;
当∠C=90°时,AE+BF=EF<CF+CE,
∴E,F不是AC,BC的中点,③错误;
作OH⊥AC于H,
∵∠BAC和∠ABC的平分线相交于点O,
∴点O在∠C的平分线上,
∴OD=OH,
∴S△CEF=×CF×OD×CE×OH=ab,④正确.
故选C.
10.【答案】D
【分析】根据等腰三角形的判定分别证出DB=DC,AB=AD,AB=CB即可.
【解答】解:图中共有等腰三角形3个,理由如下:
∵∠ADB=∠C+∠DBC,∠ADB=2∠C,
∴∠DBC=∠C,
∴△BCD是等腰三角形,DB=DC,
∵∠ABD=2∠DBC,
∴∠ABD=∠ADB,
∴△ABD是等腰三角形,AB=AD,
∵∠DBC=∠A,
∴∠A=∠C,
∴△ABC是等腰三角形,AB=CB,
故选:D.
填空题
11.【答案】100°或55°或70°
【分析】作出图形,然后分点P在AB上与BC上两种情况讨论求解.
【详解】解:①如图1,点P在AB上时,AP=AC,顶角为∠A=100°,
②∵∠ABC=25°,∠BAC=100°,
∴∠ACB=180°-25°-100°=55°,
如图2,点P在BC上时,若AC=PC,顶角为∠ACB=55°,
如图3,若AC=AP,则顶角为∠CAP=180°-2∠ACB=180°-2×55°=70°,
综上所述,顶角为105°或55°或70°.
故答案为:100°或55°或70°.
12.【答案】10°或80°或20°或140°
【分析】分三种情形:,,分别求解即可解决问题.
【详解】解:如图,
在中,,
①当时,,,
②当时,,
③当时,,
综上所述,满足条件的的值为或或或.
13.【答案】4
【分析】分AB=AP、BA=BP、PA=PB三种情况,画出图形即可得答案.
【详解】①AB=AP:以A为圆心,AB长为半径画弧,与x轴有2个交点P1、P2,
∴P1、P2,符号条件,
②BA=BP:以B为圆心,BA长为半径画弧,与x轴有2个交点P3、点(2,0),
∵点(2,0)与AB不能构成三角形,
∴P3符合条件,
③PA=PB:作线段AB的垂直平分线,与x轴有1个交点P4,
∴P4A=P4B,
∴P4符合条件,
综上所述,符合条件的点共有4个.
故答案为:4.
14.【答案】①②或①③或②③.(答案不唯一)
【分析】依据条件判定△ABE≌△DCE,即可得到AE=DE,进而得出Rt△AED是等腰三角形.
【详解】解:当AB=DC,BE=CE,∠AEB=∠DEC时,Rt△ABE≌Rt△DCE(HL),故AE=DE,即Rt△AED是等腰三角形;
当AB=DC,∠B=∠C,∠AEB=∠DEC时,△ABE≌△DCE(AAS),故AE=DE,即Rt△AED是等腰三角形;
当BE=CE,∠B=∠C,∠AEB=∠DEC时,△ABE≌△DCE(ASA),故AE=DE,即Rt△AED是等腰三角形.
故答案为:①②或①③或②③.(答案不唯一)
15.【答案】123°或132°或90°或48°
【分析】根据题意作图,结合等腰三角形的性质分情况讨论即可求解.
【详解】解:如图,若BC=CD,AD=BD,
由题意可得:∠DBC=∠BDC=(180°-∠C)÷2=82°,
∴∠ABD=∠BAD=∠BDC=41°,
∴∠ABC=∠ABD+∠DBC=123°,
∵∠ADB=180°-82°=98°,
则在BC=CD的前提下只有AD=BD;
如图,若CD=BD,AB=BD,
由题意可得:∠DBC=∠C=16°,
∴∠ADB=2∠C=32°,
∴∠A=∠ADB=32°,
∠ABD=180°-∠A-∠ADB=116°,
∴∠ABC=∠ABD+∠DBC=132°,
符合最小的内角为∠C=16°,
如图,若BD=CD,AB=AD,
则∠C=∠DBC=16°,
∴∠ADB=∠ABD=2∠C=32°,
∴∠A=180°-2×32°=116°,
∴∠ABC=∠ABD+∠DBC=48°;
如图,若BD=CD,AD=BD,
∴∠ADB=2∠C=2∠DBC=32°,
∴∠A=∠ABD=(180°-32°)÷2=74°,
∴∠ABC=∠ABD+∠DBC=90°;
若BD=BC,
则∠C=∠CDB=16°,
∴∠ADB=180°-∠CDB=164°,
则只能满足AD=BD,
∴∠A=∠CDB=8°,
即∠A<∠C,不满足;
综上:∠ABC的度数为123°或132°或90°或48°.
故答案为:123°或132°或90°或48°.
解答题
16.【解答】证明:(1)∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=36°,∠A=36°,
∴BD=AD,
即△ABD是等腰三角形;
(2)∵点E是AB的中点,
∴AE=EB,
∴∠DEB=90°,
∴∠BDE=90°﹣36°=54°.
17.【解析】(1)EF=BE+CF,
理由:∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=∠OBC,∠FCO=∠OCB,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCB,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF;
(2)不成立,
理由:∵BO平分∠ABC,CO平分∠ACD,
∴∠EBO=∠OBC,∠FCO=∠OCD,
∵EF∥BC,
∴∠EOB=∠OBC,∠FOC=∠OCD,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=OE,CF=OF,
∴EF=OE﹣OF=BE﹣CF.
故答案为EF=BE﹣CF.
18.【答案】(1)见解析;(2)见解析
【分析】(1)只要证明△ABF≌△DCE(AAS)即可;
(2)只要证明AF=DE,OF=OE即可;
【详解】证明:(1)∵BE=CF,
∴BF=CE,
∵在△ABF和△DCE中
,
∴△ABF≌△DCE(AAS),
∴AB=DC;
(2)∵△ABF≌△DCE,
∴∠AFB=∠DEC,AF=DE,
∴OE=OF,
∴AF-OF=DE-OE,
∴.
19.【详解】解:证明:∵BD=BE,
∴∠BDE=∠BED
又∵∠BED=∠CEF,
∴∠BDE=∠CEF
又∵DF⊥AC,
∴∠A+∠BDF=90°,∠C+∠CEF=90°,
∴∠A=∠C,
∴AB=BC(等角对等边),
∴△ABC是等腰三角形.
20.【解答】解:∵CA=CB,
∴设∠A=∠B=x.
∵DF=DB,
∴∠B=∠F=x,
∵AD=AE,
∴∠ADE=∠AED=∠B+∠F=2x.
在△AED中,x+2x+2x=180°,
∴x=36°,
∴∠B=∠F=36°,
∴∠BDF=180°﹣2×36°=108°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
