浙教版九上数学第三章圆的基本性质练习(含答案)
文档属性
| 名称 | 浙教版九上数学第三章圆的基本性质练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 614.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-21 14:26:25 | ||
图片预览


文档简介
浙教版九上数学第三章圆的基本性质练习
一、选择题
1.已知 的半径为5,点 在 内,则 的长可能是( )
A.7 B.6 C.5 D.4
2.下列图形中的角是圆心角的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.平分弦的直径垂直于弦
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.垂直于弦的直线平分弦
4.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
A.28° B.30° C.36° D.56°
5.如图,AB为⊙O的直径,点C在⊙O上,若,,则的长为( )
A. B. C. D.
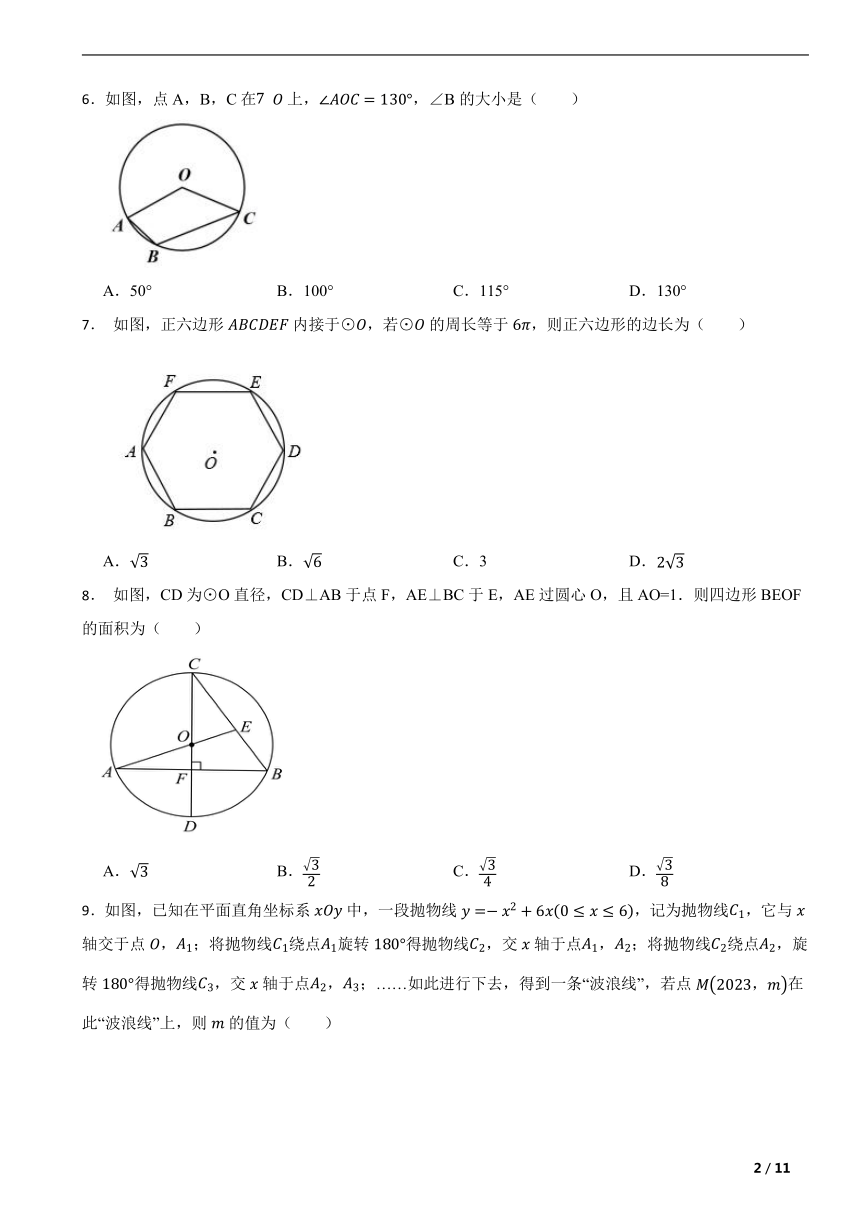
6.如图,点A,B,C在上,,∠B的大小是( )
A.50° B.100° C.115° D.130°
7. 如图,正六边形内接于⊙,若⊙的周长等于,则正六边形的边长为( )
A. B. C.3 D.
8. 如图,CD为⊙O直径,CD⊥AB于点F,AE⊥BC于E,AE过圆心O,且AO=1.则四边形BEOF的面积为( )
A. B. C. D.
9.如图,已知在平面直角坐标系中,一段抛物线,记为抛物线,它与轴交于点,;将抛物线绕点旋转得抛物线,交轴于点,;将抛物线绕点,旋转得抛物线,交轴于点,;……如此进行下去,得到一条“波浪线”,若点在此“波浪线”上,则的值为( )
A. B. C.9 D.5
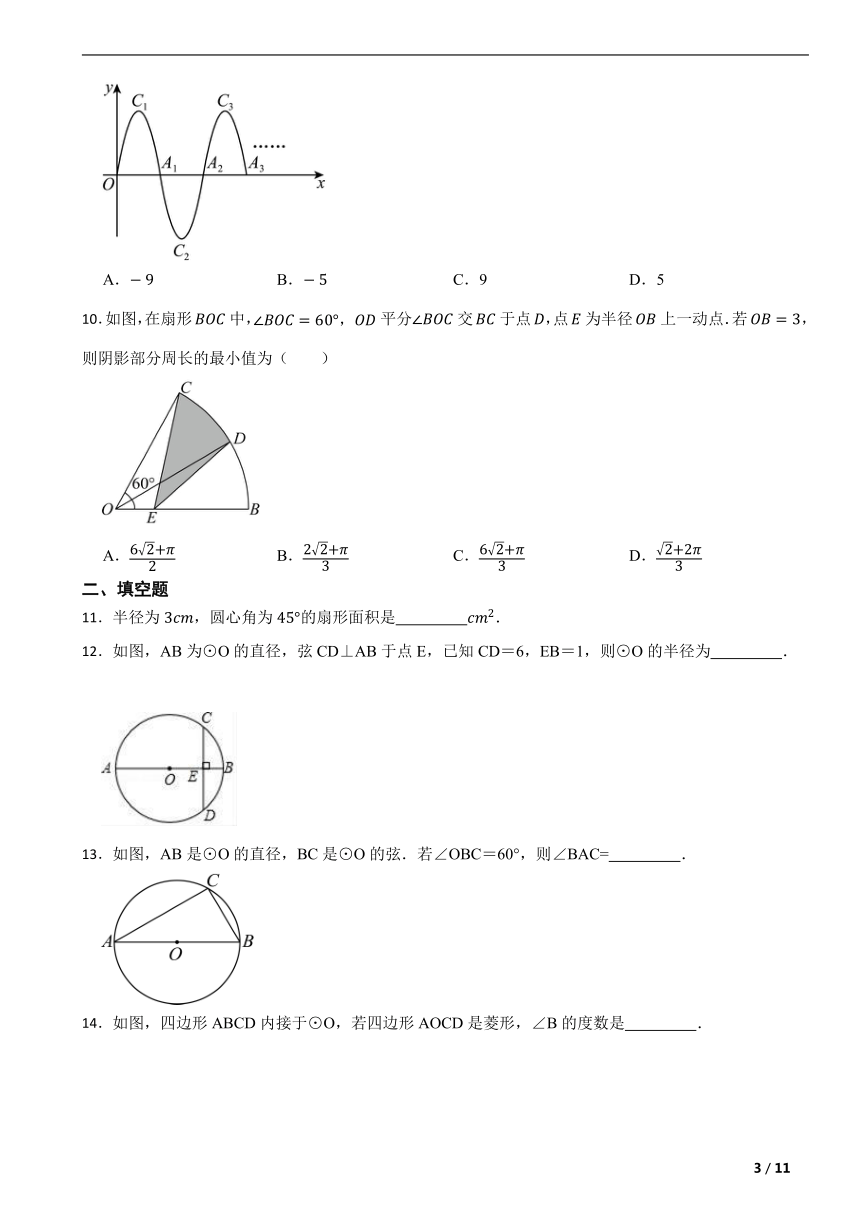
10.如图,在扇形中,平分交于点,点为半径上一动点.若,则阴影部分周长的最小值为( )
A. B. C. D.
二、填空题
11.半径为,圆心角为的扇形面积是 .
12.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为 .
13.如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC= .
14.如图,四边形ABCD内接于⊙O,若四边形AOCD是菱形,∠B的度数是 .
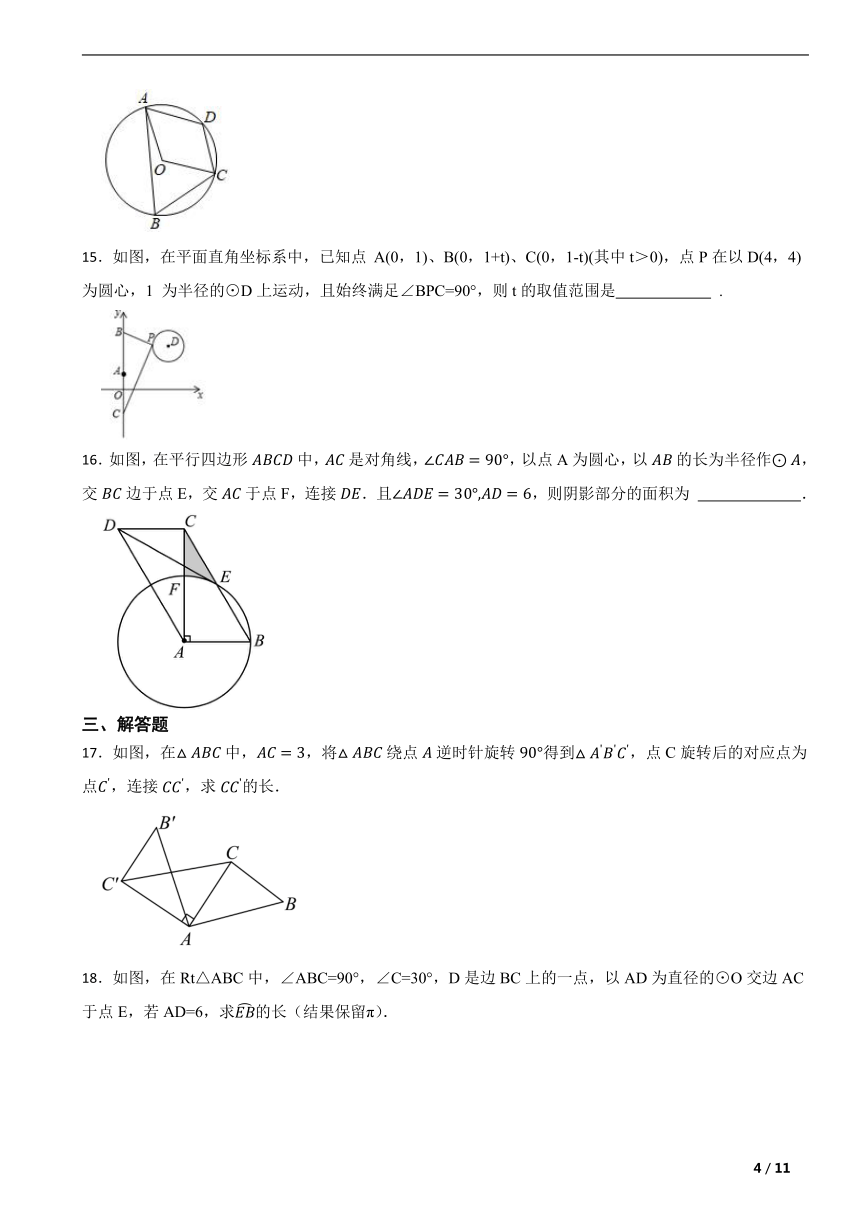
15.如图,在平面直角坐标系中,已知点 A(0,1)、B(0,1+t)、C(0,1-t)(其中t>0),点P在以D(4,4)为圆心,1 为半径的⊙D上运动,且始终满足∠BPC=90°,则t的取值范围是 .
16.如图,在平行四边形中,是对角线,,以点A为圆心,以的长为半径作,交边于点E,交于点F,连接.且,则阴影部分的面积为 .
三、解答题
17.如图,在中,,将绕点逆时针旋转得到,点C旋转后的对应点为点,连接,求的长.
18.如图,在Rt△ABC中,∠ABC=90°,∠C=30°,D是边BC上的一点,以AD为直径的⊙O交边AC于点E,若AD=6,求的长(结果保留π).
19.如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
(1)求证DB平分∠ADC,并求∠BAD的大小;
(2)过点C作CF∥AD交AB的延长线于点F,若AC=AD,BF=2求此圆半径的长
20.如图,水平放置的圆柱形排水管的截面半径为,截面中有水部分弓形的高为.
(1)求截面中弦的长;
(2)求截面中有水部分弓形的面积.
21.如图所示,AB为☉O的直径,AC是☉O的一条弦,D为的中点,作DE⊥AC于点E,交AB的延长线于点F,连接DA.
(1)若AB=90 cm,则圆心O到EF的距离是多少 说明你的理由.
(2)若DA=DF=6,求阴影部分的面积(结果保留π).
22.在中,,,为平面内的一点.
图1 图2 图3
(1)如图1,当点在边上时,,且,求的长;
(2)如图2,当点在的外部,且满足,求证:;
(3)如图3,,当、分别为、的中点时,把绕点顺时针旋转,设旋转角为,直线与的交点为,连接,直接写出旋转中面积的最大值.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】A
11.【答案】
12.【答案】5
13.【答案】30°
14.【答案】60°
15.【答案】4≤t≤6
16.【答案】
17.【答案】
18.【答案】解:解:如图,连接OB,OE,
∵∠ABC=90°,∠C=30°,
∴∠BAC=60°,
∴∠BOE=2∠BAC=120°,
∵AD=6,
∴OD=3,
∴的长为=2π.
19.【答案】(1)证明:∵∠BAC=∠ADB,∠BAC=∠CDB,∴∠ADB=∠CDB,
∴BD平分∠ADC,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
∴∠ABD+∠CBD+∠ADB+∠CDB=180°,
∴2(∠ABD+∠ADB)=180°,
∴∠ABD+∠ADB=90°,
∴∠BAD=180°-90°=90°;
(2)解:∵∠BAE+∠DAE=90°,∠BAE=∠ADE,∴∠ADE+∠DAE=90°,
∴∠AED=90°,
∵∠BAD=90°,
∴BD是圆的直径,
∴BD垂直平分AC,
∴AD=CD,
∵AC=AD,
∴△ACD是等边三角形,
∴∠ADC=60°
∵BD⊥AC,
∴,
∵CF∥AD,
∴∠F+∠BAD=180°,
∴∠F=90°,
∵四边形ABCD是圆内接四边形,
∴∠ADC+∠ABC=180°,
∵∠FBC+∠ABC=180°,
∴∠FBC=∠ADC=60°,
∴BC=2BF=4,
∵∠BCD=90°,∠BDC=30°,
∴,即BD=2BC=8,
∵BD是圆的直径,
∴圆的半径长是4.
20.【答案】(1)解:如图:
作交于,连结
∴OB=12cm.
是圆心,,
cm,
(cm),
(cm),
cm.
即弦AB长cm.
(2)解:连结
,,
,
(cm2).
即截面中有水部分弓形的面积为cm2.
21.【答案】(1)解:如图所示,连接OD,
∵D为的中点,
∴∠CAD=∠BAD.
∵OA=OD,
∴∠BAD=∠ADO.
∴∠CAD=∠ADO.∴OD∥AE.
∵DE⊥AC,∴OD⊥EF.
∴OD的长是圆心O到EF的距离.
∵AB=90 cm,∴OD=AB=45 cm.
(2)解:如图所示,过点O作OG⊥AD交AD于点G.
∵DA=DF,∴∠F=∠BAD.
由(1),得∠CAD=∠BAD,
∴∠F=∠CAD.
∵∠F+∠BAD+∠CAD=90°,
∴∠F=∠BAD=∠CAD=30°.
∴∠BOD=2∠BAD=60°,OF=2OD.
∵在Rt△ODF中,OF2-OD2=DF2,
∴(2OD)2-OD2=(6)2,解得OD=6.
在Rt△OAG中,OA=OD=6,∠OAG=30°,AG==3,AD=2,
S△AOD=×6×3=9.
∴S阴影=S扇形OBD+S△AOD=+9=6π+9.
22.【答案】(1)解:如图,将沿折叠,得到,连接,
∵,
∴,
将沿折叠,得到,
∴
∴,,,
∴,
∴为等边三角形,为等腰直角三角形
∴,
∴;
(2)证明:如图,过作,且,连接,
∵
∴,
又∵,
∴
∴
又∵,
∴,,即
,,
∴
∴;
(3)解: 的面积最大值为.
1 / 1
一、选择题
1.已知 的半径为5,点 在 内,则 的长可能是( )
A.7 B.6 C.5 D.4
2.下列图形中的角是圆心角的是( )
A. B.
C. D.
3.下列说法正确的是( )
A.平分弦的直径垂直于弦
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.垂直于弦的直线平分弦
4.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
A.28° B.30° C.36° D.56°
5.如图,AB为⊙O的直径,点C在⊙O上,若,,则的长为( )
A. B. C. D.
6.如图,点A,B,C在上,,∠B的大小是( )
A.50° B.100° C.115° D.130°
7. 如图,正六边形内接于⊙,若⊙的周长等于,则正六边形的边长为( )
A. B. C.3 D.
8. 如图,CD为⊙O直径,CD⊥AB于点F,AE⊥BC于E,AE过圆心O,且AO=1.则四边形BEOF的面积为( )
A. B. C. D.
9.如图,已知在平面直角坐标系中,一段抛物线,记为抛物线,它与轴交于点,;将抛物线绕点旋转得抛物线,交轴于点,;将抛物线绕点,旋转得抛物线,交轴于点,;……如此进行下去,得到一条“波浪线”,若点在此“波浪线”上,则的值为( )
A. B. C.9 D.5
10.如图,在扇形中,平分交于点,点为半径上一动点.若,则阴影部分周长的最小值为( )
A. B. C. D.
二、填空题
11.半径为,圆心角为的扇形面积是 .
12.如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为 .
13.如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC= .
14.如图,四边形ABCD内接于⊙O,若四边形AOCD是菱形,∠B的度数是 .
15.如图,在平面直角坐标系中,已知点 A(0,1)、B(0,1+t)、C(0,1-t)(其中t>0),点P在以D(4,4)为圆心,1 为半径的⊙D上运动,且始终满足∠BPC=90°,则t的取值范围是 .
16.如图,在平行四边形中,是对角线,,以点A为圆心,以的长为半径作,交边于点E,交于点F,连接.且,则阴影部分的面积为 .
三、解答题
17.如图,在中,,将绕点逆时针旋转得到,点C旋转后的对应点为点,连接,求的长.
18.如图,在Rt△ABC中,∠ABC=90°,∠C=30°,D是边BC上的一点,以AD为直径的⊙O交边AC于点E,若AD=6,求的长(结果保留π).
19.如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
(1)求证DB平分∠ADC,并求∠BAD的大小;
(2)过点C作CF∥AD交AB的延长线于点F,若AC=AD,BF=2求此圆半径的长
20.如图,水平放置的圆柱形排水管的截面半径为,截面中有水部分弓形的高为.
(1)求截面中弦的长;
(2)求截面中有水部分弓形的面积.
21.如图所示,AB为☉O的直径,AC是☉O的一条弦,D为的中点,作DE⊥AC于点E,交AB的延长线于点F,连接DA.
(1)若AB=90 cm,则圆心O到EF的距离是多少 说明你的理由.
(2)若DA=DF=6,求阴影部分的面积(结果保留π).
22.在中,,,为平面内的一点.
图1 图2 图3
(1)如图1,当点在边上时,,且,求的长;
(2)如图2,当点在的外部,且满足,求证:;
(3)如图3,,当、分别为、的中点时,把绕点顺时针旋转,设旋转角为,直线与的交点为,连接,直接写出旋转中面积的最大值.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】C
9.【答案】B
10.【答案】A
11.【答案】
12.【答案】5
13.【答案】30°
14.【答案】60°
15.【答案】4≤t≤6
16.【答案】
17.【答案】
18.【答案】解:解:如图,连接OB,OE,
∵∠ABC=90°,∠C=30°,
∴∠BAC=60°,
∴∠BOE=2∠BAC=120°,
∵AD=6,
∴OD=3,
∴的长为=2π.
19.【答案】(1)证明:∵∠BAC=∠ADB,∠BAC=∠CDB,∴∠ADB=∠CDB,
∴BD平分∠ADC,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
∴∠ABD+∠CBD+∠ADB+∠CDB=180°,
∴2(∠ABD+∠ADB)=180°,
∴∠ABD+∠ADB=90°,
∴∠BAD=180°-90°=90°;
(2)解:∵∠BAE+∠DAE=90°,∠BAE=∠ADE,∴∠ADE+∠DAE=90°,
∴∠AED=90°,
∵∠BAD=90°,
∴BD是圆的直径,
∴BD垂直平分AC,
∴AD=CD,
∵AC=AD,
∴△ACD是等边三角形,
∴∠ADC=60°
∵BD⊥AC,
∴,
∵CF∥AD,
∴∠F+∠BAD=180°,
∴∠F=90°,
∵四边形ABCD是圆内接四边形,
∴∠ADC+∠ABC=180°,
∵∠FBC+∠ABC=180°,
∴∠FBC=∠ADC=60°,
∴BC=2BF=4,
∵∠BCD=90°,∠BDC=30°,
∴,即BD=2BC=8,
∵BD是圆的直径,
∴圆的半径长是4.
20.【答案】(1)解:如图:
作交于,连结
∴OB=12cm.
是圆心,,
cm,
(cm),
(cm),
cm.
即弦AB长cm.
(2)解:连结
,,
,
(cm2).
即截面中有水部分弓形的面积为cm2.
21.【答案】(1)解:如图所示,连接OD,
∵D为的中点,
∴∠CAD=∠BAD.
∵OA=OD,
∴∠BAD=∠ADO.
∴∠CAD=∠ADO.∴OD∥AE.
∵DE⊥AC,∴OD⊥EF.
∴OD的长是圆心O到EF的距离.
∵AB=90 cm,∴OD=AB=45 cm.
(2)解:如图所示,过点O作OG⊥AD交AD于点G.
∵DA=DF,∴∠F=∠BAD.
由(1),得∠CAD=∠BAD,
∴∠F=∠CAD.
∵∠F+∠BAD+∠CAD=90°,
∴∠F=∠BAD=∠CAD=30°.
∴∠BOD=2∠BAD=60°,OF=2OD.
∵在Rt△ODF中,OF2-OD2=DF2,
∴(2OD)2-OD2=(6)2,解得OD=6.
在Rt△OAG中,OA=OD=6,∠OAG=30°,AG==3,AD=2,
S△AOD=×6×3=9.
∴S阴影=S扇形OBD+S△AOD=+9=6π+9.
22.【答案】(1)解:如图,将沿折叠,得到,连接,
∵,
∴,
将沿折叠,得到,
∴
∴,,,
∴,
∴为等边三角形,为等腰直角三角形
∴,
∴;
(2)证明:如图,过作,且,连接,
∵
∴,
又∵,
∴
∴
又∵,
∴,,即
,,
∴
∴;
(3)解: 的面积最大值为.
1 / 1
同课章节目录
