浙教版数学八年级上册5.5一次函数的简单应用 精品同步练习(含解析)
文档属性
| 名称 | 浙教版数学八年级上册5.5一次函数的简单应用 精品同步练习(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-21 20:15:51 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
浙教版八年级上册数学 5.5一次函数的简单应用 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.已知一次函数y=kx+b的图象经过第一,二,三象限,且与x轴交于点(﹣2,0),则不等式kx+b>0的解是( )
A.x>﹣2 B.x>2 C.x<﹣2 D.x<2
2.已知不等式ax+b<0的解是x>﹣2,下列有可能是函数y=ax+b的图象的是( )
A. B.
C. D.
3.如图,购买一种苹果,付款金额(元与购买量(千克)之间的函数图象由线段和射线组成,则一次购买5千克这种苹果比分五次每次购买1千克这种苹果可节省
A.4 元 B.5 元 C.6 元 D.7 元
4.受国际金融危机影响,市自来水公司号召全市市民节约用水.决定采取月用水量分段收费办法,某户居民应交水费(元与用水量(吨的函数关系如图所示.若该用户本月用水21吨,则应交水费
A.52.5元 B.45元 C.42元 D.37.8元
5.如图,反映了某公司产品的销售收入与销售量的关系;反映了该公司产品的销售成本与销售量的关系.根据图象判断,该公司盈利时,销售量
A. B. C. D.
6.端午节至,甲、乙两队参加了一年一度的赛龙舟比赛,两队在比赛时的路程(米与时间(秒之间的函数图象如图所示,请你根据图象判断,下列说法错误的是
A.甲队率先到达终点
B.甲队比乙队多走了126米
C.在47.8秒时,甲、乙两队所走的路程相等
D.乙队全程所花的时间为90.2秒
7.一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为(小时),两车之间的距离为(千米),如图中的折线表示与之间的函数关系,下列说法:①甲、乙两地相距1000千米;②点的实际意义是两车出发3小时后相遇;③普通列车从乙地到达甲地时间是9小时;④动车的速度是270千米小时,其中不正确的有
A.4个 B.3个 C.2个 D.1个
8.甲、乙两人相约从地到地,甲骑自行车先行,乙开车,两人均在同一路线上匀速行驶,乙到地后即停车等甲.甲、乙两人之间的距离(千米)与甲行驶的时间(小时)之间的函数关系如图所示,则乙从地到地所用的时间为
A.0.25小时 B.0.5小时 C.1小时 D.2.5小时
9.甲、乙两人在直线跑道上同起点,同终点,同方向匀速跑200米,先到终点的人原地休息.已知甲先跑8米,乙才出发,在跑步过程中,甲、乙两人的距离(单位:米)与乙出发的时间(单位:秒)之间的关系如图所示,则图中的值是
A.44 B.46 C.48 D.50
10.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返速度的大小不变,两车离乙地的距离(单位:与慢车行驶时间(单位:的函数关系如图,则两车先后两次相遇的间隔时间是
A. B. C. D.
二、填空题(本大题共5小题,每小题4分,共20分。)
11.过(0,4)且与直线y=2x平行的直线的表达式是 .
12.某市政府大力扶持大学生创业.小甬在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量(件与销售单价(元之间的关系可近似地看作一次函数:.根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果小甬想要每月获得的利润不低于2000元,那么他每月的成本最少需要 元.(成本进价销售量)
13.某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中,分别表示去年、今年水费(元与用水量之间的关系.小雨家去年用水量为,若今年用水量与去年相同,水费将比去年多 元.
14.学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离(米与时间(分钟)之间的函数关系如图所示.乙回到学校用了 分钟.
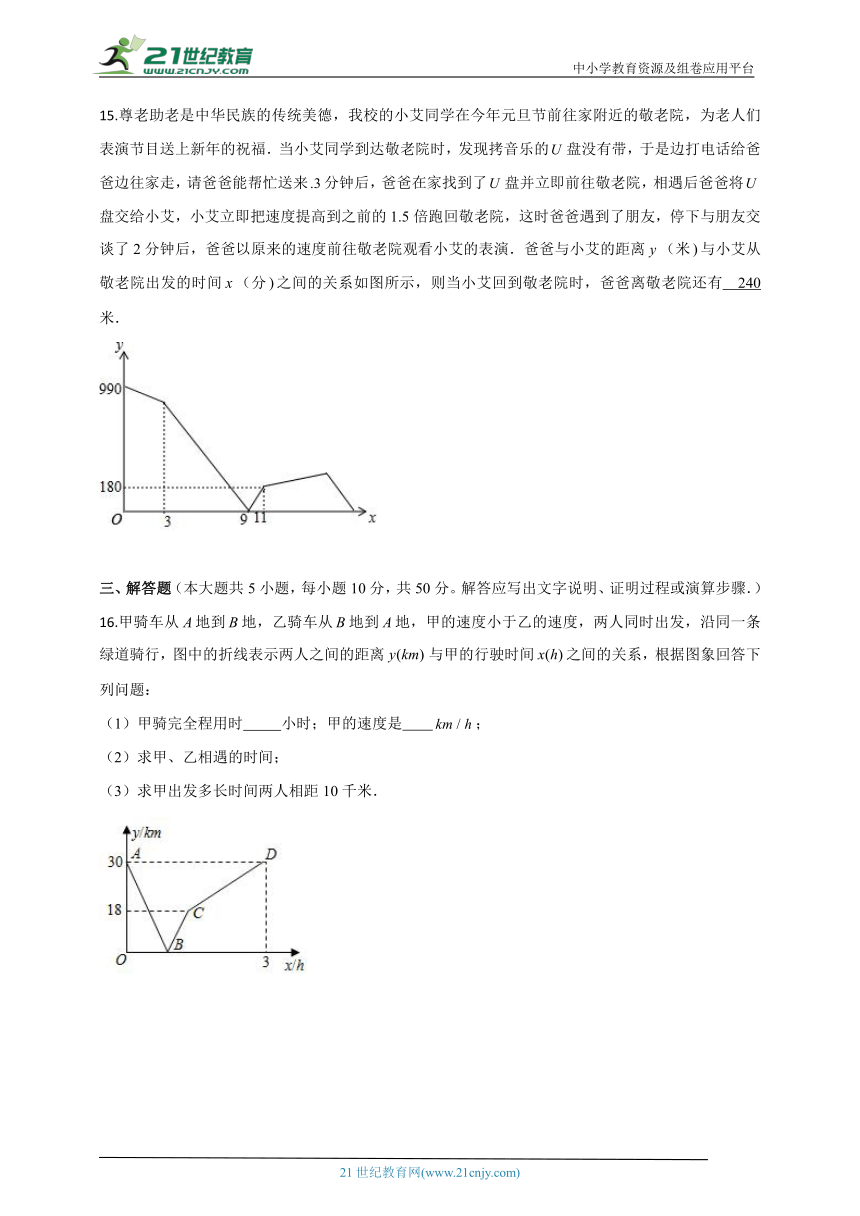
15.尊老助老是中华民族的传统美德,我校的小艾同学在今年元旦节前往家附近的敬老院,为老人们表演节目送上新年的祝福.当小艾同学到达敬老院时,发现拷音乐的盘没有带,于是边打电话给爸爸边往家走,请爸爸能帮忙送来分钟后,爸爸在家找到了盘并立即前往敬老院,相遇后爸爸将盘交给小艾,小艾立即把速度提高到之前的1.5倍跑回敬老院,这时爸爸遇到了朋友,停下与朋友交谈了2分钟后,爸爸以原来的速度前往敬老院观看小艾的表演.爸爸与小艾的距离(米与小艾从敬老院出发的时间(分之间的关系如图所示,则当小艾回到敬老院时,爸爸离敬老院还有 240 米.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.甲骑车从地到地,乙骑车从地到地,甲的速度小于乙的速度,两人同时出发,沿同一条绿道骑行,图中的折线表示两人之间的距离与甲的行驶时间之间的关系,根据图象回答下列问题:
(1)甲骑完全程用时 小时;甲的速度是 ;
(2)求甲、乙相遇的时间;
(3)求甲出发多长时间两人相距10千米.
17.如图,在平面直角坐标系中,已知点A(1,0),B(0,﹣2),直线y=﹣x+4与x轴交于点C,与y轴交于点D,且交直线AB于点E.
(1)求直线AB的函数解析式;
(2)求△ACE的面积;
(3)若点F为直线AB上的一点,且满足S△ACF=3S△ACE,求点F的坐标.
18.元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离(千米)与汽车行驶时间(小时)之间的函数图象.
(1)求小黄出发0.5小时时,离家的距离;
(2)求出段的图象的函数解析式;
(3)小黄出发1.5小时时,离目的地还有多少千米?
19.甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)设先由甲队施工天,再由乙队施工天,刚好完成筑路任务,求与之间的函数关系式.
(3)在(2)的条件下,若每天需付给甲队的筑路费用为0.1万元,需付给乙队的筑路费用为0.2万元,且甲、乙两队施工的总天数不超过24天,则如何安排甲、乙两队施工的天数,使施工费用最少,并求出最少费用.
20.为减少碳排量,提倡使用新能源汽车,给汽车商家带来了商机.某汽车行经营的型新能源汽车去年销售总额为9000万元.今年该型新能源汽车每辆售价预计比去年降低2万元.若该型新能源汽车的今年销售数量是去年的1.2倍,那么今年的销售总额将比去年多600万元.
(1)求型号新能源汽车去年售价每辆多少万元?
(2)该汽车行今年计划新进一批型新能源汽车和新款型新能源汽车共60辆,且型新能源汽车的进货数量不超过型新能源汽车数量的两倍.已知,型车和型车的进货价格分别为每辆15万元和每辆18万元,计划型车销售价格为每辆20万元,应如何组织进货才能使该汽车行这批新能源车销售后获利最多?
参考答案
选择题
1.【分析】先由一次函数y=kx+b的图象经过一、二、三象限,则函数y随x的增大而增大,得出k>0,再由y=kx+b的图象与x轴交于点(﹣2,0),确定不等式kx+b>0的解集.
【解答】解:∵一次函数y=kx+b的图象经过一、二、三象限,则函数y随x的增大而增大,
∴k>0.
∵一次函数y=kx+b的图象与x轴交于点(﹣2,0),即当x=﹣2时,y=0,
∴关于x的不等式kx+b>0的解集是x>﹣2.
故选:A.
2.【分析】由不等式ax+b<0的解是x>﹣2可得直线y=ax+b与x轴交点为(﹣2,0)且y随x增大而减小,进而求解.
【解答】解:∵不等式ax+b<0的解是x>﹣2,
∴直线y=ax+b与x轴交点为(﹣2,0)且y随x增大而减小,
故选:D.
3.【分析】利用待定系数法可分别求得直线、的函数解析式,再分别求得两种方式所需费用,即可求得答案.
【解析】
由图象可知,,
设直线解析式为,则,解得,
直线解析式为,
买1千克时,付款金额为,
分五次购买1千克所需要费用为50元,
设直线解析式为,
,解得,
直线解析式为,
当时,,即一次购买5千克所需费用为44元,
,
一次购买5千克这种苹果比分五次每次购买1千克这种苹果可节省6元,
故选:.
4.【分析】由图象知用水量不超过15吨时水费为(元吨),超过部分为(元吨).搞清楚价格后再计算就好办了.
【解析】设直线解析式为,把,,代入得:,
解之得:即,当时,.
故选:.
5.【分析】要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
【解析】由图意可知:的轴表示的是销售收入,的轴表示的是销售成本.
盈利需要销售收入大于销售成本,应是的函数图象高于的函数图象,那么.
故选:.
6.【分析】根据函数图象中的数据,可以判断各个选项中的说法是否正确,从而可以解答本题.
【解析】由图象可得,
甲队率先到达终点,故选项正确;
甲队和乙队走的一样多,故选项错误;
在47.8秒时,甲、乙两队所走的路程相等,故选项正确;
乙队全程所花的时间为90.2秒,故选项正确;
故选:.
7.【分析】根据题意和函数图象中的数据可以判断各个小题中的结论是否正确,从而可以解答本题.
【解答】解解:由图象可得,
甲、乙两地相距1000千米,
故①正确;
出发后3小时,两车之间的距离为0,
可知点的实际意义是两车出发后3小时相遇,
故②正确;
由图象可得,普通列车从乙地到达甲地时间是12小时,
故③不正确;
普通列车的速度是(千米小时),
设动车的速度为千米小时,
根据题意,得:,
解得:,
动车的速度为250千米小时,
故④不正确;
故选:.
8.【分析】根据速度路程时间,可求甲骑自行车的速度为千米小时,根据乙出发0.25小时追上甲,设乙速度为千米小时,列方程求出乙速度,设追上后到达地的时间是小时,根据追击路程列方程求解,再把两个时间相加即可求解.
【解析】由图像可得:甲骑自行车的速度为千米小时,乙出发0.25小时追上甲,
设乙速度为千米小时,
,
解得:,
乙速度为50千米小时,
设追上后到达地的时间是,
,
解得:,
乙从地到地所用的时间为(小时),
故选:.
9.【分析】乙的速度为(米秒),由追击问题可以求出甲的速度,即可得出结论.
【解析】由题意,得
乙的速度为:(米秒),
甲的速度为:(米秒),
(秒.
故选:.
10.【分析】根据图象得出,慢车的速度为,快车的速度为.从而得出快车和慢车对应的与的函数关系式.联立两个函数关系式,求解出图象对应两个交点的坐标,即可得出间隔时间.
【解析】根据图象可知,慢车的速度为.
对于快车,由于往返速度大小不变,总共行驶时间是,
故其速度为.
所以对于慢车,与的函数表达式为①.
对于快车,设当时,与的函数表达式为,
由题意得:,
解得:,
对于快车,当时,与的函数表达式为②,
对于快车,设当时,与的函数表达式为,
由题意得:,
解得:,
对于快车,当时,与的函数表达式为③,
联立①②,可解得交点横坐标为,
联立①③,可解得交点横坐标为,
因此,两车先后两次相遇的间隔时间是,
故选:.
填空题
11.【分析】根据两平行直线的解析式的k值相等求出k,再把经过的点的坐标代入函数解析式计算求出b,从而得解.
【解答】解:设直线l的函数解析式为一次函数y=kx+b,
∵它的图象平行于直线y=2x,
∴k=2,
∵直线l经过点(0,4),
∴b=4,
∴这个一次函数的解析式为y=2x+4.
故答案为:y=2x+4.
12.【分析】设成本为(元,根据题意得出与的函数关系式,再根据一次函数的性质解答即可.
【解析】设成本为(元,由题意,得:,
,
随的增大而减小,
由,
当时,,
当时,,
(元,
答:想要每月获得的利润不低于2000元,每月的成本最少为3600元.
故答案为:3600.
13.【分析】根据题意和函数图象中的数据,可以计算出今年用水量与去年相同,水费将比去年多多少元.
【解析】由图象可得,
去年用水量时,需缴纳水费480元,今年用水量时,需缴纳水费720元,
今年用水量与去年相同,水费将比去年多(元,
故答案为:240.
14.【分析】根据题意和函数图象中的数据,可以先求出甲的速度,然后根据图象可知24分钟两人相遇,从而可以求得乙的速度,然后即可得到乙回到学校用的时间.
【解析】由图象可得,
甲的速度为:(米分钟),
乙的速度为:(米分钟),
则乙回到学校用了:(分钟),
故答案为:40.
15.【分析】根据函数图象中的数据可知,在9分钟到11分钟小艾走的路程是180米,用时2分钟,从而可以求得此时的速度,即小艾提速后的速度,然后即可得到小艾开始的速度,再根据两人9分钟相遇,可以求得爸爸的速度,再根据题意和图象中的数据即可计算出当小艾回到敬老院时,爸爸离敬老院还有多少米.
【解析】由题意可得,
小艾的原来的速度为:(米分钟),
爸爸的速度为:(米分钟),
9分钟的时候,小艾离敬老院的距离为:(米,
小艾最后回到敬老院的时间为:(分钟),
当小艾回到敬老院时,爸爸离敬老院还有:(米,
故答案为:240.
解答题
16.【分析】(1)根据题意和函数图象中的数据可以求得甲骑完全程所用的时间和速度;
(2)根据相同时间甲、乙的速度之比等于路程之比可求出乙的速度,则可求出甲、乙相遇的时间;
(3)分甲、乙相遇前和相遇后两种情况列出方程可求出答案.
【解析】(1)由图象可知,甲骑完全程用时3小时,
甲的速度是.
故答案为:3;10.
(2)由题意可知,乙到地时,甲距离地18千米处,
相同时间甲、乙的速度之比等于路程之比,
,
相遇时间为;
(3)①甲、乙相遇前,,
解得,;
②甲、乙相遇后,且未到地时,,
解得,;
综合以上可得,当或时,两人相距10千米.
17.【分析】(1)待定系数法求解析式即可;
(2)先求出点C坐标,再联立求出点E坐标,再根据三角形面积公式计算即可;
(3)设点F坐标为(m,2m﹣2),根据S△ACF=3S△ACE,可得S△ACF==9,进一步求解即可.
【解答】解:(1)设直线AB的函数解析式为y=kx+b(k≠0),
代入点A(1,0),B(0,﹣2),
得,
解得,
∴直线AB的解析式为y=2x﹣2;
(2)令y=﹣x+4=0,
解得x=4,
∴点C坐标为(4,0),
∵A(1,0),
∴AC=3,
联立,
解得,
∴点E坐标为(2,2),
∴=3;
(3)设点F坐标为(m,2m﹣2),
∵S△ACF=3S△ACE,
∴S△ACF==9,
∴|2m﹣2|=6,
解得m=4或m=﹣2,
∴点F坐标为(4,6)或(﹣2,﹣6).
18.【分析】(1)先运用待定系数法求出的解析式,再将代入,求出的值即可;
(2)设段图象的函数表达式为,将、两点的坐标代入,运用待定系数法即可求解;
(3)先将代入段图象的函数表达式,求出对应的值,再用156减去即可求解.
【解析】(1)设段图象的函数表达式为.
当时,,
,
.
,
当时,.
故小黄出发0.5小时时,离家30千米;
(2)设段图象的函数表达式为.
,在上,
,
解得,
;
(3)当时,,
.
故小黄出发1.5小时时,离目的地还有45千米.
19.【分析】(1)设乙队完成此项任务需要天,则甲队完成此项任务天,然后根据甲队单独施工45天和队单独施工30天的工作量相同,可以得到相应的分式方程,从而可以得到甲、乙两队单独完成此项任务各需多少天;
(2)根据题意,可以得到与的函数关系式;
(3)根据(2)中的条件和题意,可以得到总费用与甲施工天数之间的函数关系式,然后利用一次函数的性质,即可解答本题,
【解析】(1)设乙队完成此项任务需要天,则甲队完成此项任务天,
,
解得,,
经检验,是原分式方程的解,
,
答:甲、乙两队单独完成此项任务各需30天、20天;
(2)由题意可得,
,
化简,得
,
即与之间的函数关系式是;
(3)设施工的总费用为元,
,
甲、乙两队施工的总天数不超过24天,
,
即,
解得,,
当时,取得最小值,此时,,
答:安排甲施工12天、乙施工12天,使施工费用最少,最少费用是3.6万元.
20.【分析】(1)设型号新能源汽车去年售价每辆万元,销售量为辆,根据今年和去年的销售额列方程组,解方程组即可;
(2)设型号新能源汽车进辆,则型号新能源汽车进辆,利润为万元,根据利润等于售价乘以销售量列出函数关系式,再根据型新能源汽车的进货数量不超过型新能源汽车数量的两倍,即,得出的取值范围,根据函数的性质求最值即可.
【解析】(1)设型号新能源汽车去年售价每辆万元,销售量为辆,
则今年型号新能源汽车售价每辆万元,销售量为辆,
由题意得:,
解得:,
答:型号新能源汽车去年售价每辆18万元.
(2)设型号新能源汽车进辆,则型号新能源汽车进辆,利润为万元,
今年型新能源汽车每辆售价预计比去年降低2万元,
今年型新能源汽车每辆售价(万元)
由题意得:,
型新能源汽车的进货数量不超过型新能源汽车数量的两倍,
,
解得:,
,
随的增大而减小,
当时,最大,最大值为:(万元),
此时(辆
购买型号新能源汽车20辆,购买型号新能源汽车40辆,销售后利润最大.
答:购买型号新能源汽车20辆,购买型号新能源汽车40辆,销售后利润最大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版八年级上册数学 5.5一次函数的简单应用 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.已知一次函数y=kx+b的图象经过第一,二,三象限,且与x轴交于点(﹣2,0),则不等式kx+b>0的解是( )
A.x>﹣2 B.x>2 C.x<﹣2 D.x<2
2.已知不等式ax+b<0的解是x>﹣2,下列有可能是函数y=ax+b的图象的是( )
A. B.
C. D.
3.如图,购买一种苹果,付款金额(元与购买量(千克)之间的函数图象由线段和射线组成,则一次购买5千克这种苹果比分五次每次购买1千克这种苹果可节省
A.4 元 B.5 元 C.6 元 D.7 元
4.受国际金融危机影响,市自来水公司号召全市市民节约用水.决定采取月用水量分段收费办法,某户居民应交水费(元与用水量(吨的函数关系如图所示.若该用户本月用水21吨,则应交水费
A.52.5元 B.45元 C.42元 D.37.8元
5.如图,反映了某公司产品的销售收入与销售量的关系;反映了该公司产品的销售成本与销售量的关系.根据图象判断,该公司盈利时,销售量
A. B. C. D.
6.端午节至,甲、乙两队参加了一年一度的赛龙舟比赛,两队在比赛时的路程(米与时间(秒之间的函数图象如图所示,请你根据图象判断,下列说法错误的是
A.甲队率先到达终点
B.甲队比乙队多走了126米
C.在47.8秒时,甲、乙两队所走的路程相等
D.乙队全程所花的时间为90.2秒
7.一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为(小时),两车之间的距离为(千米),如图中的折线表示与之间的函数关系,下列说法:①甲、乙两地相距1000千米;②点的实际意义是两车出发3小时后相遇;③普通列车从乙地到达甲地时间是9小时;④动车的速度是270千米小时,其中不正确的有
A.4个 B.3个 C.2个 D.1个
8.甲、乙两人相约从地到地,甲骑自行车先行,乙开车,两人均在同一路线上匀速行驶,乙到地后即停车等甲.甲、乙两人之间的距离(千米)与甲行驶的时间(小时)之间的函数关系如图所示,则乙从地到地所用的时间为
A.0.25小时 B.0.5小时 C.1小时 D.2.5小时
9.甲、乙两人在直线跑道上同起点,同终点,同方向匀速跑200米,先到终点的人原地休息.已知甲先跑8米,乙才出发,在跑步过程中,甲、乙两人的距离(单位:米)与乙出发的时间(单位:秒)之间的关系如图所示,则图中的值是
A.44 B.46 C.48 D.50
10.一辆快车和一辆慢车将一批物资从甲地运往乙地,其中快车送达后立即沿原路返回,且往返速度的大小不变,两车离乙地的距离(单位:与慢车行驶时间(单位:的函数关系如图,则两车先后两次相遇的间隔时间是
A. B. C. D.
二、填空题(本大题共5小题,每小题4分,共20分。)
11.过(0,4)且与直线y=2x平行的直线的表达式是 .
12.某市政府大力扶持大学生创业.小甬在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量(件与销售单价(元之间的关系可近似地看作一次函数:.根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果小甬想要每月获得的利润不低于2000元,那么他每月的成本最少需要 元.(成本进价销售量)
13.某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中,分别表示去年、今年水费(元与用水量之间的关系.小雨家去年用水量为,若今年用水量与去年相同,水费将比去年多 元.
14.学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离(米与时间(分钟)之间的函数关系如图所示.乙回到学校用了 分钟.
15.尊老助老是中华民族的传统美德,我校的小艾同学在今年元旦节前往家附近的敬老院,为老人们表演节目送上新年的祝福.当小艾同学到达敬老院时,发现拷音乐的盘没有带,于是边打电话给爸爸边往家走,请爸爸能帮忙送来分钟后,爸爸在家找到了盘并立即前往敬老院,相遇后爸爸将盘交给小艾,小艾立即把速度提高到之前的1.5倍跑回敬老院,这时爸爸遇到了朋友,停下与朋友交谈了2分钟后,爸爸以原来的速度前往敬老院观看小艾的表演.爸爸与小艾的距离(米与小艾从敬老院出发的时间(分之间的关系如图所示,则当小艾回到敬老院时,爸爸离敬老院还有 240 米.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.甲骑车从地到地,乙骑车从地到地,甲的速度小于乙的速度,两人同时出发,沿同一条绿道骑行,图中的折线表示两人之间的距离与甲的行驶时间之间的关系,根据图象回答下列问题:
(1)甲骑完全程用时 小时;甲的速度是 ;
(2)求甲、乙相遇的时间;
(3)求甲出发多长时间两人相距10千米.
17.如图,在平面直角坐标系中,已知点A(1,0),B(0,﹣2),直线y=﹣x+4与x轴交于点C,与y轴交于点D,且交直线AB于点E.
(1)求直线AB的函数解析式;
(2)求△ACE的面积;
(3)若点F为直线AB上的一点,且满足S△ACF=3S△ACE,求点F的坐标.
18.元旦期间,小黄自驾游去了离家156千米的黄石矿博园,右图是小黄离家的距离(千米)与汽车行驶时间(小时)之间的函数图象.
(1)求小黄出发0.5小时时,离家的距离;
(2)求出段的图象的函数解析式;
(3)小黄出发1.5小时时,离目的地还有多少千米?
19.甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.
(1)甲、乙两队单独完成此项任务各需多少天?
(2)设先由甲队施工天,再由乙队施工天,刚好完成筑路任务,求与之间的函数关系式.
(3)在(2)的条件下,若每天需付给甲队的筑路费用为0.1万元,需付给乙队的筑路费用为0.2万元,且甲、乙两队施工的总天数不超过24天,则如何安排甲、乙两队施工的天数,使施工费用最少,并求出最少费用.
20.为减少碳排量,提倡使用新能源汽车,给汽车商家带来了商机.某汽车行经营的型新能源汽车去年销售总额为9000万元.今年该型新能源汽车每辆售价预计比去年降低2万元.若该型新能源汽车的今年销售数量是去年的1.2倍,那么今年的销售总额将比去年多600万元.
(1)求型号新能源汽车去年售价每辆多少万元?
(2)该汽车行今年计划新进一批型新能源汽车和新款型新能源汽车共60辆,且型新能源汽车的进货数量不超过型新能源汽车数量的两倍.已知,型车和型车的进货价格分别为每辆15万元和每辆18万元,计划型车销售价格为每辆20万元,应如何组织进货才能使该汽车行这批新能源车销售后获利最多?
参考答案
选择题
1.【分析】先由一次函数y=kx+b的图象经过一、二、三象限,则函数y随x的增大而增大,得出k>0,再由y=kx+b的图象与x轴交于点(﹣2,0),确定不等式kx+b>0的解集.
【解答】解:∵一次函数y=kx+b的图象经过一、二、三象限,则函数y随x的增大而增大,
∴k>0.
∵一次函数y=kx+b的图象与x轴交于点(﹣2,0),即当x=﹣2时,y=0,
∴关于x的不等式kx+b>0的解集是x>﹣2.
故选:A.
2.【分析】由不等式ax+b<0的解是x>﹣2可得直线y=ax+b与x轴交点为(﹣2,0)且y随x增大而减小,进而求解.
【解答】解:∵不等式ax+b<0的解是x>﹣2,
∴直线y=ax+b与x轴交点为(﹣2,0)且y随x增大而减小,
故选:D.
3.【分析】利用待定系数法可分别求得直线、的函数解析式,再分别求得两种方式所需费用,即可求得答案.
【解析】
由图象可知,,
设直线解析式为,则,解得,
直线解析式为,
买1千克时,付款金额为,
分五次购买1千克所需要费用为50元,
设直线解析式为,
,解得,
直线解析式为,
当时,,即一次购买5千克所需费用为44元,
,
一次购买5千克这种苹果比分五次每次购买1千克这种苹果可节省6元,
故选:.
4.【分析】由图象知用水量不超过15吨时水费为(元吨),超过部分为(元吨).搞清楚价格后再计算就好办了.
【解析】设直线解析式为,把,,代入得:,
解之得:即,当时,.
故选:.
5.【分析】要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件,结合实际意义得到正确的结论.
【解析】由图意可知:的轴表示的是销售收入,的轴表示的是销售成本.
盈利需要销售收入大于销售成本,应是的函数图象高于的函数图象,那么.
故选:.
6.【分析】根据函数图象中的数据,可以判断各个选项中的说法是否正确,从而可以解答本题.
【解析】由图象可得,
甲队率先到达终点,故选项正确;
甲队和乙队走的一样多,故选项错误;
在47.8秒时,甲、乙两队所走的路程相等,故选项正确;
乙队全程所花的时间为90.2秒,故选项正确;
故选:.
7.【分析】根据题意和函数图象中的数据可以判断各个小题中的结论是否正确,从而可以解答本题.
【解答】解解:由图象可得,
甲、乙两地相距1000千米,
故①正确;
出发后3小时,两车之间的距离为0,
可知点的实际意义是两车出发后3小时相遇,
故②正确;
由图象可得,普通列车从乙地到达甲地时间是12小时,
故③不正确;
普通列车的速度是(千米小时),
设动车的速度为千米小时,
根据题意,得:,
解得:,
动车的速度为250千米小时,
故④不正确;
故选:.
8.【分析】根据速度路程时间,可求甲骑自行车的速度为千米小时,根据乙出发0.25小时追上甲,设乙速度为千米小时,列方程求出乙速度,设追上后到达地的时间是小时,根据追击路程列方程求解,再把两个时间相加即可求解.
【解析】由图像可得:甲骑自行车的速度为千米小时,乙出发0.25小时追上甲,
设乙速度为千米小时,
,
解得:,
乙速度为50千米小时,
设追上后到达地的时间是,
,
解得:,
乙从地到地所用的时间为(小时),
故选:.
9.【分析】乙的速度为(米秒),由追击问题可以求出甲的速度,即可得出结论.
【解析】由题意,得
乙的速度为:(米秒),
甲的速度为:(米秒),
(秒.
故选:.
10.【分析】根据图象得出,慢车的速度为,快车的速度为.从而得出快车和慢车对应的与的函数关系式.联立两个函数关系式,求解出图象对应两个交点的坐标,即可得出间隔时间.
【解析】根据图象可知,慢车的速度为.
对于快车,由于往返速度大小不变,总共行驶时间是,
故其速度为.
所以对于慢车,与的函数表达式为①.
对于快车,设当时,与的函数表达式为,
由题意得:,
解得:,
对于快车,当时,与的函数表达式为②,
对于快车,设当时,与的函数表达式为,
由题意得:,
解得:,
对于快车,当时,与的函数表达式为③,
联立①②,可解得交点横坐标为,
联立①③,可解得交点横坐标为,
因此,两车先后两次相遇的间隔时间是,
故选:.
填空题
11.【分析】根据两平行直线的解析式的k值相等求出k,再把经过的点的坐标代入函数解析式计算求出b,从而得解.
【解答】解:设直线l的函数解析式为一次函数y=kx+b,
∵它的图象平行于直线y=2x,
∴k=2,
∵直线l经过点(0,4),
∴b=4,
∴这个一次函数的解析式为y=2x+4.
故答案为:y=2x+4.
12.【分析】设成本为(元,根据题意得出与的函数关系式,再根据一次函数的性质解答即可.
【解析】设成本为(元,由题意,得:,
,
随的增大而减小,
由,
当时,,
当时,,
(元,
答:想要每月获得的利润不低于2000元,每月的成本最少为3600元.
故答案为:3600.
13.【分析】根据题意和函数图象中的数据,可以计算出今年用水量与去年相同,水费将比去年多多少元.
【解析】由图象可得,
去年用水量时,需缴纳水费480元,今年用水量时,需缴纳水费720元,
今年用水量与去年相同,水费将比去年多(元,
故答案为:240.
14.【分析】根据题意和函数图象中的数据,可以先求出甲的速度,然后根据图象可知24分钟两人相遇,从而可以求得乙的速度,然后即可得到乙回到学校用的时间.
【解析】由图象可得,
甲的速度为:(米分钟),
乙的速度为:(米分钟),
则乙回到学校用了:(分钟),
故答案为:40.
15.【分析】根据函数图象中的数据可知,在9分钟到11分钟小艾走的路程是180米,用时2分钟,从而可以求得此时的速度,即小艾提速后的速度,然后即可得到小艾开始的速度,再根据两人9分钟相遇,可以求得爸爸的速度,再根据题意和图象中的数据即可计算出当小艾回到敬老院时,爸爸离敬老院还有多少米.
【解析】由题意可得,
小艾的原来的速度为:(米分钟),
爸爸的速度为:(米分钟),
9分钟的时候,小艾离敬老院的距离为:(米,
小艾最后回到敬老院的时间为:(分钟),
当小艾回到敬老院时,爸爸离敬老院还有:(米,
故答案为:240.
解答题
16.【分析】(1)根据题意和函数图象中的数据可以求得甲骑完全程所用的时间和速度;
(2)根据相同时间甲、乙的速度之比等于路程之比可求出乙的速度,则可求出甲、乙相遇的时间;
(3)分甲、乙相遇前和相遇后两种情况列出方程可求出答案.
【解析】(1)由图象可知,甲骑完全程用时3小时,
甲的速度是.
故答案为:3;10.
(2)由题意可知,乙到地时,甲距离地18千米处,
相同时间甲、乙的速度之比等于路程之比,
,
相遇时间为;
(3)①甲、乙相遇前,,
解得,;
②甲、乙相遇后,且未到地时,,
解得,;
综合以上可得,当或时,两人相距10千米.
17.【分析】(1)待定系数法求解析式即可;
(2)先求出点C坐标,再联立求出点E坐标,再根据三角形面积公式计算即可;
(3)设点F坐标为(m,2m﹣2),根据S△ACF=3S△ACE,可得S△ACF==9,进一步求解即可.
【解答】解:(1)设直线AB的函数解析式为y=kx+b(k≠0),
代入点A(1,0),B(0,﹣2),
得,
解得,
∴直线AB的解析式为y=2x﹣2;
(2)令y=﹣x+4=0,
解得x=4,
∴点C坐标为(4,0),
∵A(1,0),
∴AC=3,
联立,
解得,
∴点E坐标为(2,2),
∴=3;
(3)设点F坐标为(m,2m﹣2),
∵S△ACF=3S△ACE,
∴S△ACF==9,
∴|2m﹣2|=6,
解得m=4或m=﹣2,
∴点F坐标为(4,6)或(﹣2,﹣6).
18.【分析】(1)先运用待定系数法求出的解析式,再将代入,求出的值即可;
(2)设段图象的函数表达式为,将、两点的坐标代入,运用待定系数法即可求解;
(3)先将代入段图象的函数表达式,求出对应的值,再用156减去即可求解.
【解析】(1)设段图象的函数表达式为.
当时,,
,
.
,
当时,.
故小黄出发0.5小时时,离家30千米;
(2)设段图象的函数表达式为.
,在上,
,
解得,
;
(3)当时,,
.
故小黄出发1.5小时时,离目的地还有45千米.
19.【分析】(1)设乙队完成此项任务需要天,则甲队完成此项任务天,然后根据甲队单独施工45天和队单独施工30天的工作量相同,可以得到相应的分式方程,从而可以得到甲、乙两队单独完成此项任务各需多少天;
(2)根据题意,可以得到与的函数关系式;
(3)根据(2)中的条件和题意,可以得到总费用与甲施工天数之间的函数关系式,然后利用一次函数的性质,即可解答本题,
【解析】(1)设乙队完成此项任务需要天,则甲队完成此项任务天,
,
解得,,
经检验,是原分式方程的解,
,
答:甲、乙两队单独完成此项任务各需30天、20天;
(2)由题意可得,
,
化简,得
,
即与之间的函数关系式是;
(3)设施工的总费用为元,
,
甲、乙两队施工的总天数不超过24天,
,
即,
解得,,
当时,取得最小值,此时,,
答:安排甲施工12天、乙施工12天,使施工费用最少,最少费用是3.6万元.
20.【分析】(1)设型号新能源汽车去年售价每辆万元,销售量为辆,根据今年和去年的销售额列方程组,解方程组即可;
(2)设型号新能源汽车进辆,则型号新能源汽车进辆,利润为万元,根据利润等于售价乘以销售量列出函数关系式,再根据型新能源汽车的进货数量不超过型新能源汽车数量的两倍,即,得出的取值范围,根据函数的性质求最值即可.
【解析】(1)设型号新能源汽车去年售价每辆万元,销售量为辆,
则今年型号新能源汽车售价每辆万元,销售量为辆,
由题意得:,
解得:,
答:型号新能源汽车去年售价每辆18万元.
(2)设型号新能源汽车进辆,则型号新能源汽车进辆,利润为万元,
今年型新能源汽车每辆售价预计比去年降低2万元,
今年型新能源汽车每辆售价(万元)
由题意得:,
型新能源汽车的进货数量不超过型新能源汽车数量的两倍,
,
解得:,
,
随的增大而减小,
当时,最大,最大值为:(万元),
此时(辆
购买型号新能源汽车20辆,购买型号新能源汽车40辆,销售后利润最大.
答:购买型号新能源汽车20辆,购买型号新能源汽车40辆,销售后利润最大.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
