2024-2025学年九年级上册数学第一章 二次函数单元培优测试(大讲堂)(含详解)
文档属性
| 名称 | 2024-2025学年九年级上册数学第一章 二次函数单元培优测试(大讲堂)(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 546.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 09:37:03 | ||
图片预览



文档简介
二次函数单元测试培优强基卷
一、选择题(每题3分,共30分)
1.二次函数中,自变量与函数的对应值如下表:
若,则下面叙述正确的是( )
A.该函数图象开口向上
B.该函数图象与轴的交点在轴的下方
C.对称轴是直线
D.若是方程的正数解,则
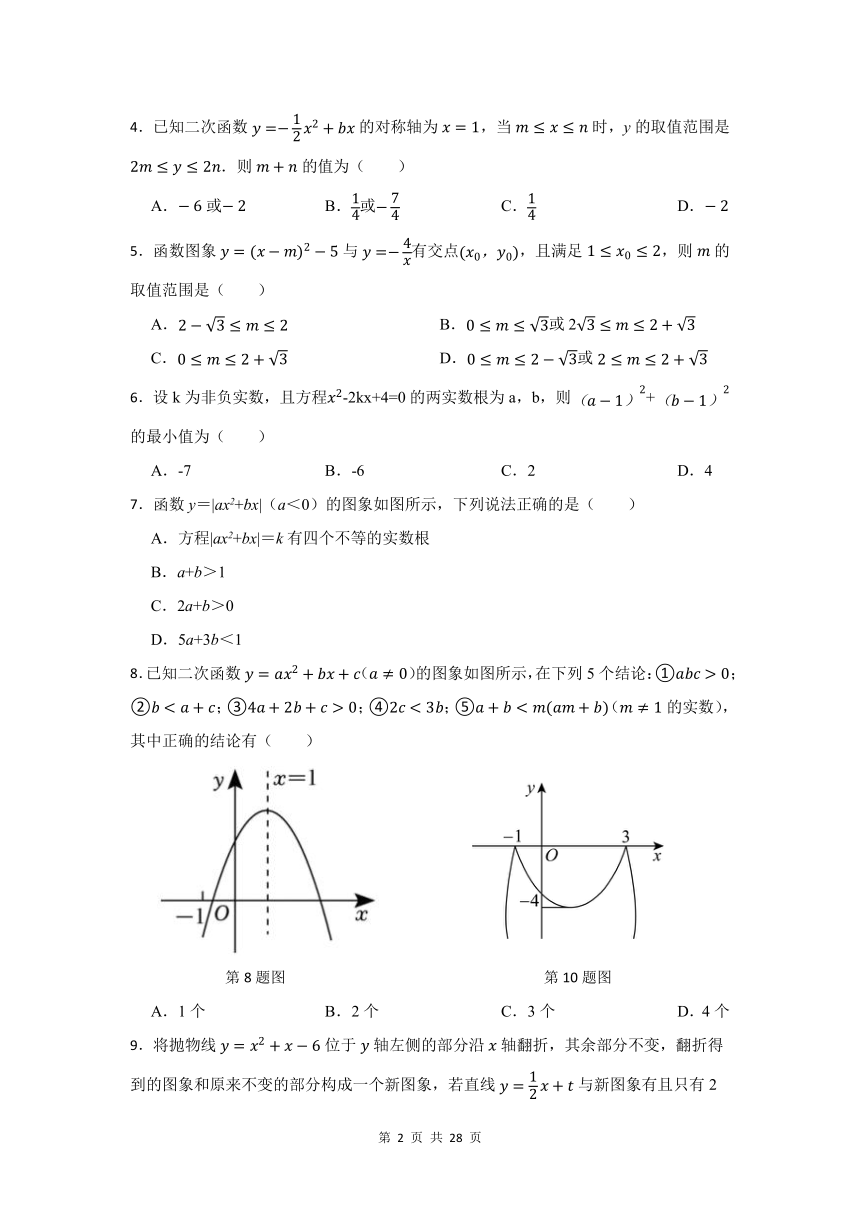
2.如图,二次函数的图象与x轴的交点为A、D的横坐标分别为3和,其图像与x轴围成封闭图形L,图形L内部(不包含边界)恰有4个整点(横纵坐标均为整数的点),系数a的值可以是( )
第2题图 第7题图
A. B. C. D.
3.定义:在平面直角坐标系中,若点A满足横、纵坐标都为整数,则把点A叫做“整点”.如:B(3,0)、C(﹣1,3)都是“整点”.抛物线y=ax2﹣2ax+a+2(a<0)与x轴交于点M,N两点,若该抛物线在M、N之间的部分与线段MN所围的区域(包括边界)恰有5个整点,则a的取值范围是( )
A.﹣1≤a<0 B.﹣2≤a<﹣1
C.﹣1≤a< D.﹣2≤a<0
4.已知二次函数的对称轴为,当时,y的取值范围是.则的值为( )
A.或 B.或 C. D.
5.函数图象与有交点,且满足,则的取值范围是( )
A. B.或2
C. D.或
6.设k为非负实数,且方程-2kx+4=0的两实数根为a,b,则+的最小值为( )
A.-7 B.-6 C.2 D.4
7.函数y=|ax2+bx|(a<0)的图象如图所示,下列说法正确的是( )
A.方程|ax2+bx|=k有四个不等的实数根
B.a+b>1
C.2a+b>0
D.5a+3b<1
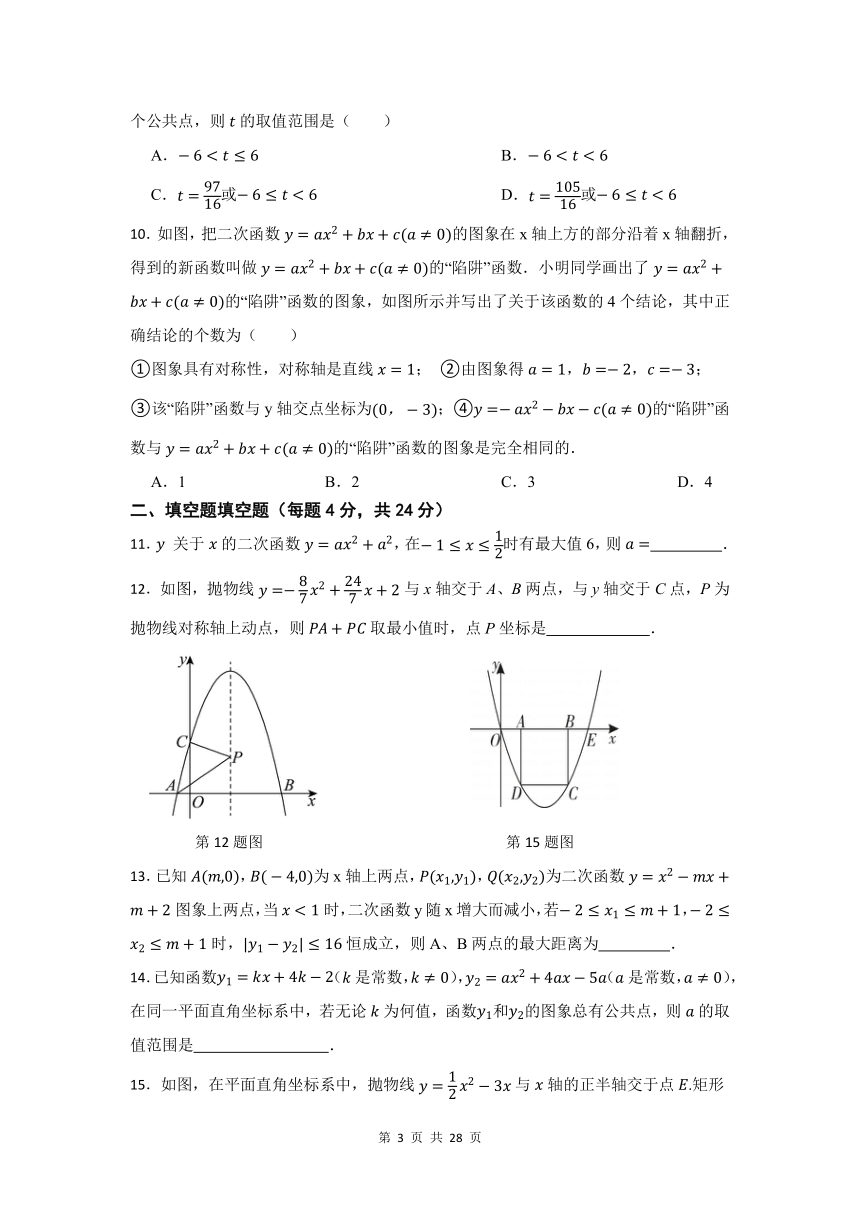
8.已知二次函数()的图象如图所示,在下列5个结论:①;②;③;④;⑤(的实数),其中正确的结论有( )
第8题图 第10题图
A.1个 B.2个 C.3个 D.4个
9.将抛物线位于轴左侧的部分沿轴翻折,其余部分不变,翻折得到的图象和原来不变的部分构成一个新图象,若直线与新图象有且只有2个公共点,则的取值范围是( )
A. B.
C.或 D.或
10.如图,把二次函数的图象在x轴上方的部分沿着x轴翻折,得到的新函数叫做的“陷阱”函数.小明同学画出了的“陷阱”函数的图象,如图所示并写出了关于该函数的4个结论,其中正确结论的个数为( )
①图象具有对称性,对称轴是直线; ②由图象得,,;
③该“陷阱”函数与y轴交点坐标为;④的“陷阱”函数与的“陷阱”函数的图象是完全相同的.
A.1 B.2 C.3 D.4
二、填空题填空题(每题4分,共24分)
11. 关于的二次函数,在时有最大值6,则 .
12.如图,抛物线与x轴交于A、B两点,与y轴交于C点,P为抛物线对称轴上动点,则取最小值时,点P坐标是 .
第12题图 第15题图
13.已知,为x轴上两点,,为二次函数图象上两点,当时,二次函数y随x增大而减小,若,时,恒成立,则A、B两点的最大距离为 .
14.已知函数(是常数,),(是常数,),在同一平面直角坐标系中,若无论为何值,函数和的图象总有公共点,则的取值范围是 .
15.如图,在平面直角坐标系中,抛物线与轴的正半轴交于点.矩形的边在线段上,点C、D在抛物线上,则矩形周长的最大值为 .
16.已知抛物线y=ax2+bx+c(a,b,c是常数,a<0)经过点(2,0),且2①方程ax2+bx+c=0有两个不相等的实数根;
②若对任意的实数m,都有bm-b≥am2-a,则
③若抛物线经过点(-1,0),在抛物线上有且仅有2个点到x轴的距离等于n(n>0),则;
④点A(x1,y1),B(x2,y2)在抛物线上,且都在y轴右侧,若4a+c>0,则(x1-x2)(y1-y2)>0.
其中正确的是 (填写序号).
三、综合题(17-21每题6分,22、23每题8分,共46分)
17. 如图,△ABC中,,,,,反比例函数的图象与AB交于点,与BC交于点E.
(1)求m,k的值;
(2)点P为反比例函数图象上一动点(点P在D,E之间运动,不与D,E重合),过点P作,交y轴于点M,过点P作轴,交BC于点N,连接MN,求△PMN面积的最大值,并求出此时点P的坐标.
18.如图,对称轴为直线的抛物线与轴相交于,两点,其中点的坐标为,且点在抛物线上.
(1)求抛物线的解析式;
(2)点为抛物线与轴的交点;
①点在抛物线上,且,求点点坐标;
②设点是线段上的动点,作轴交抛物线于点,求线段长度的最大值.
19.如图,已知二次函数 的图象经过点 ,与 轴分别交于点 ,点 .点 是直线 上方的抛物线上一动点.
(1)求二次函数 的表达式;
(2)连接 , ,并把 沿 轴翻折,得到四边形 .若四边形 为菱形,请求出此时点 的坐标;
(3)当点 运动到什么位置时,四边形 的面积最大?求出此时 点的坐标和四边形 的最大面积.
20.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+2与x轴相交于A(﹣1,0),B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是直线BC上方抛物线上一动点,连接PB,PC,求△PBC面积的最大值以及此时点P的坐标;
(3)抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
21.如图1,已知抛物线与x轴交于点和点,与y轴交于点C.
(1)求b和c的值;
(2)已知点D是在第一象限内的抛物线上的一点,过点D作轴于点E.
①如图2,点D是抛物线的顶点,点P是上一点,若,求点P的坐标;
②如图3,若与交于点F,连接,且,求点D的坐标.
图1 图2 图3
22.如图,直线AB与抛物线交于、两点,与y轴交于点C,点D为线段AB上一点,连接OD、OB.
(1)求抛物线的解析式;
(2)若OD将分成面积相等的两部分,求点D的坐标;
(3)在平面坐标内是否存在点P,使得以A、O、B、P为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
23.如图1,在平面直角坐标中,抛物线与x轴交于点、两点,与y轴交于点C,连接,直线交y轴于点M.P为直线上方抛物线上一动点,过点P作x轴的垂线,分别交直线、于点E、F.
(1)求抛物线的表达式;
(2)当点P落在抛物线的对称轴上时,求的面积;
(3)若点N为y轴上一动点,当四边形为矩形时,求点N的坐标;
答案解析部分
1.【答案】D
【解答】根据表格可知
若,
A:该函数图象开口向上,叙述错误,图象开口应向下,不符合题意
B:该函数图象与轴的交点在轴的下方,叙述错误,函数图象与轴的交点在轴的上方,不符合题意
C:对称轴是直线,叙述错误,对称轴是直线,不符合题意
D:若是方程的正数解,则,叙述正确,当 时,,有,符合题意
故选:D
2.【答案】B
【解答】解:∵二次函数的图象与x轴的交点为A、D的横坐标分别为3和,
∴二次函数解析式为,对称轴为直线,
当时,,,
∴抛物线顶点坐标为,与y轴的交点坐标为,
如图所示:
∵图形L内部(不包含边界)恰有4个整点(横纵坐标均为整数的点),
∴,
解得,
∴四个选项中只有B选项符合题意,
故答案为:B
【解答】解:抛物线y=ax2﹣2ax+a+2(a<0)化为顶点式为y=a(x﹣1)2+2,故函数的对称轴:x=1,M和N两点关于x=1对称,根据题意,抛物线在M、N之间的部分与线段MN所围的区域(包括边界)恰有5个整点,这些整点是(0,0),(1,0),((1,1),(1,2),(2,0),
如图所示:
∵当x=0时,y=a+2
∴0≤a+2<1
当x=﹣1时,y=4a+2<0
即:,
解得﹣2≤a<﹣1
故选B.
4.【答案】D
【解答】解:∵二次函数的对称轴为,
∴,即,
∴,
当时,有最大值,
∴,
∴,
∴当时,随的增大而增大,
∴,,
解得:或;或;
经检验时,不符合题意;
∴,,
∴.
故答案为:D
5.【答案】D
【解答】解:如图,
函数 图象与函数有交点 ,且满足
对于函数,当x=1时,y=(1-m)2-5;当x=2时,y=(2-m)2-5;
对于函数,当x=1时,y=-4;当x=2时,y=-2;
若二次函数在对称轴右侧的部分与反比例函数有交点,且满足
从图中观察可得:
由①得:0≤m≤2
由②得:m≤2-3或m>2+3
∴0≤m≤2-3 ;
若二次函数在对称轴左侧的部分与反比例函数有交点,且满足
从图中观察可得:
由①得:m≤0或m≥2
由②得:2-3≤m≤2+3 ∴2≤m≤2+ 3 综上所述, 或
故答案为:D.
6.【答案】C
【解答】解:∵x2-2kx+4=0有两个实数根
∴ =(-2k)2-4×4=4k2-16≥0
∴k2≥4
∵k为非负实数
∴k≥2
由韦达定理得:a+b=2k,ab=4
∴(a-1)+(b-1)=2k-2,
(a-1)(b-1)=ab-(a+b)+1=4-2k+1=5-2k
∴(a-1)2+(b-1)2=[(a-1)+(b-1)]2-2(a-1)(b-1)=(2k-2)2-2(5-2k)=4(k-)2-7
令y=4(k-12)2-7,则函数图象开口向上,在对称轴右侧,y随k的增大而增大
∴当k=2时,y有最小值4(2-12)2-7=2,即 + 的最小值为2
故答案为:C.
7.【答案】D
【解答】解:A、由题意得当时,方程 |ax2+bx| =k没有实数根,故选项A错误;
B、由题意得时, ,当x=1时,,故选项B错误;
C、由题意得,∴,故选项C错误;
D、由题意得时, ,当时, ,
当x=1时,①,
当x=2时,,即②,
由①+②得 5a+3b<1
故答案为:D.
8.【答案】B
【解答】解∶开口向下,;对称轴在轴的右侧,a、b异号,则;抛物线与轴的交点在轴的上方,,则,所以①不正确;
当时图象在轴下方,则,即,所以②不正确;
对称轴为直线,则时图象在轴上方,则,所以③正确;
,则,而,则,所以④正确;
开口向下,当有最大值;
当时,,则,即,所以⑤正不确.
故答案为:B.
9.【答案】D
【解答】解: ,
令y=0,则x2+x-6=0,解得x=-3,y=2,
抛物线与x轴交点为(-3,0),(2,0),
由题意可得翻折后y轴左侧的抛物线为,
当直线经过点(0,-6) 时,得t=-6,此时直线与新图象有且只有2个公共点,
然后将直线向上平移过程中直至经过(0,6)之前,始终与新图象有且只有2个公共点,
把(0,6)代入中得t=6,
∴-6≤t<6时,直线与新图象有且只有2个公共点,
联立与,令y值相等,得=,
整理为2x2+3x+2t-12=0,
△=32+4×2(2t-12)=0,解得t=,
当t=,直线与新图象有且只有2个公共点,
∴或.
故答案为:D.
10.【答案】C
【解答】解:①∵二次函数的图象与x轴的交点为:,,
∴二次函数图象的对称轴为直线,故此说法正确;
②由函数图象可知,原二次函数的顶点坐标为,
∴该二次函数的解析式为:,
把代入得:,
解得:,
∴
,
∴,,,故原说法错误;
③把代入得:,
∴原函数与y轴的交点坐标为,
∵把二次函数的图象在x轴上方的部分沿着x轴翻折,得到的新函数叫做的“陷阱”函数,
∴该“陷阱”函数与y轴交点坐标为,故此说法正确;
④∵,
∴的图象与的图象关于x轴对称,
∴的“陷阱”函数与的“陷阱”函数的图象是完全相同,故此说法正确;
综上分析可知,正确的结论有3个,
故答案为:C
11.【答案】2或
【解答】解:y=ax2+a2,
①当a>0时,二次函数的对称轴为x=0,
∴x=-1时,ymax=a+a2=6,
解得:a=2或a=-3(舍去);
②当a<0时,二次函数的对称轴为x=0,
∴x=0时,ymax=a2=6,
解得:a=或a=(舍去),
综上所述,a=2或.
故答案为:2或.
12.【答案】
【解答】解:如图所示:连接BC,交抛物线对称轴于点P,根据的对称性可知,此时取得最小值,
令x=0,则y=2,
点C坐标为(0,2),
令y=0,则,
解得:
点B坐标为,
设直线BC的表达式为y=kx+b,
将点C坐标(0,2),点B坐标代入y=kx+b,
得:,
解得:,
直线BC的表达式为,
抛物线的对称轴,
点P的横坐标为,
把x=代入,
解得y=,
点P的坐标为 .
故答案为: .
13.【答案】8
【解答】解:当x=1时,y=3,
抛物线y=x2-mx+m+2的对称轴为直线,
∵当x<1时,二次函数y随x增大而减小,
,
∴m≥2.
∴m+1≥3,
当x=-2时,y=6+3m,当时,,
∵-2≤x1≤m+1,-2≤x2≤m+1,
∴|y1-y2|的最大值为,
∵|y1-y2|≤16恒成立,
.
∴-12≤m≤4,
∵m≥2,
∴2≤m≤4,
∴m的最大值为4,
∴A、B两点的最大距离为4-(-4)=8.
故答案为:8.
14.【答案】或
【解答】且 ,
该函数过点(-4,-2),
且 ,
该函数过(-5,0),(1,0)
当a<0时,无论k为何值,函数和的图象总有公共点,
a<0符合题意;
当a>0时,无论k为何值,函数和的图象总有公共点,
x=-4时,可得
解得
符合题意;
无论为何值,函数和的图象总有公共点,则的取值范围为或 .
15.【答案】13
【解答】设点D的横坐标为m,则点D的纵坐标为,
∴AD=,
∵抛物线的对称轴是直线,
∴点C的横坐标为3-(m-3)=6-m,
∴CD=2m-6,
∴矩形ABCD的周长=,
∴当m=5时,矩形周长有最大值为13,
故答案为:13.
16.【答案】①②③
【解答】解:①∵a<0, 2∴,
∴方程ax2+bx+c=0有两个不相等的实数根 ,结论①正确;
②∵y=ax2+bx+c,经过点(2,0),∴4a+2b+c=0.
若对任意的实数m,都有bm-b≥am2-a ,即-am2+bm+a-b≥0总成立,
则,
∵总成立,
∴b-2a=0,b=2a.
∴4a+2b+c=8a+c=0,c=-8a.
∵2∴2<-8a<3,
∴,结论②正确;
③∵抛物线经过点(-1,0) 和 点(2,0)时,对称轴为,
∴4a+2b+c=0,a-b+c=0,
解得:a+b=0,
∴b=-a,
c=-a+b=-2a,
当时,抛物线有最大值
当 时,抛物线上有4个点到x轴的距离等于n;
当 时,抛物线上有3个点到x轴的距离等于n;
当 时,抛物线上有且仅有2个点到x轴的距离等于n;结论③正确;
④∵4a+2b+c=0,∴4a+c=-2b>0,∴b<0,
故对称轴,
∵a<0,∴抛物线开口向下,在对称轴右侧y随x的增大而减小.
∵点A(x1,y1),B(x2,y2)在抛物线上,且都在y轴右侧,
故x1y2,即(x1-x2)(y1-y2)<0,结论④错误;
故答案为:①②③.
17.【答案】(1)解:,,.
又,.
,点.
设直线AB的函数表达式为,
将,代入,得
∴直线AB的函数表达式为.
将点代入,得.
.
将代入,得.
(2)解:延长NP交y轴于点Q,交AB于点L.
,,.
轴,,.
,,,.
设点P的坐标为,,则,.
.
.
当时,有最大值,此时.
18.【答案】(1)解:抛物线的对称轴为直线,
又点与在抛物线上,
,
解得,
抛物线的解析式为
(2)解:①由(1)知,二次函数的解析式为,
抛物线与轴的交点的坐标为,与轴的另一交点为,
则,,
设点坐标为,
,
,
,
则,
当时,,
当时,,
点的坐标为或;
②如图,
设直线的解析式为,
将,代入得,
解得,
直线的解析式为,
设点坐标为,,
则点坐标为,
,
当时,线段的长度有最大值.
19.【答案】(1)解:将点B和点C的坐标代入 ,
得 ,解得 , .
∴ 该二次函数的表达式为 .
(2)解:若四边形POP′C是菱形,则点P在线段CO的垂直平分线上;如图,连接PP′,则PE⊥CO,垂足为E,∵ C(0,3),∴ E(0, ),∴ 点P的纵坐标等于 .∴ ,解得 , (不合题意,舍去),
∴ 点P的坐标为( , ).
(3)解:过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(m, ),设直线BC的表达式为 ,则 , 解得 .
∴直线BC的表达式为 .
∴Q点的坐标为(m, ),
∴ .
当 ,
解得 ,∴ AO=1,AB=4,
∴ S四边形ABPC =S△ABC+S△CPQ+S△BPQ
=
=
当 时,四边形ABPC的面积最大.
此时P点的坐标为 ,四边形ABPC的面积的最大值为 .
20.【答案】(1)解:把A(﹣1,0),B(4,0)代入y=ax2+bx+2得:
,
解得,
∴抛物线的解析式为;
(2)解:过P作PK∥y轴交BC于K,如图:
在中,令x=0得y=2,
∴C(0,2),
由B(4,0),C(0,2)得直线BC解析式为,
设P(t,),则K,
∴PK=
∴S△PBC=,
∵﹣1<0,
∴当t=2时,S△PBC取最大值4,此时P(2,3),
∴△PBC面积的最大值为4,此时点P的坐标为(2,3);
(3)解:抛物线上存在点Q,使∠QCB=45°,理由如下:
当Q在BC上方时,过B作BT⊥CQ于T,过T作MN⊥y轴于N,过B作BM⊥MN于M,如图:
∵∠QCB=45°,
∴△BCT是等腰直角三角形,
∴∠BTC=90°,BT=CT,
∴∠CTN=90°﹣∠BTM=∠TBM,
∵∠M=∠TNC=90°,
∴△BTM≌△TCN(AAS),
∴BM=NT,TM=CN,
设T(m,n),则NT=m,BM=n,
∵B(4,0),C(0,2),
∴TM=MN﹣NT=4﹣m,CN=ON﹣OC=n﹣2,
∵BM=NT,TM=CN,
∴,
解得
∴T(3,3),
由C(0,2),T(3,3)得直线CT解析式为,
联立,
解得,
∴Q();
当Q在BC下方时,过B作BR⊥CQ于R,过R作SW⊥y轴于W,过B作BS⊥SW于S,如图:
同理可得△BSR≌△RWC(AAS),
∴BS=RW,RS=CW,
设R(p,q),
∴,
解得,
∴R(1,﹣1),
∴直线CR解析式为y=﹣3x+2,
联立,
解得 ,
∴Q(9,﹣25),
综上所述,Q的坐标为()或(9,﹣25).
21.【答案】(1)解:将点和点代入抛物线中,
得,
解得,
所以,;
故
(2)解:①由(1)知抛物线的表达式为
,抛物线的顶点D的坐标为
设点P的坐标为,
根据勾股定理,得,,
,
,
即,
解得.
点P的坐标为;
②设直线的函数表达式为
把点和点代入,
得,
解得
直线的函数表达式为
设点E的坐标为,则点,点
,
则,.
由,得
整理得,
解得,(不符合题意,舍去),
当时,
点D的坐标为.
22.【答案】(1)解:由题意可得,
,解得:,
∴抛物线的解析式为:;
(2)解:设直线AB的解析式为:,则
,解得:,
∴直线AB的解析式为:,
设点D的坐标为(m,m+4),
∵OD将△分成面积相等的两部分,即,
∴,解得:,
∴点D的坐标为(-1,3);
(3)解:存在;
设点P的坐标为(xp,yp),
①当四边形AOBP是平行四边形时,p1在第二象限时,
轴,,
∵B(2,6),
∴点P的坐标为(-2,6);
②当四边形AOPB是平行四边形时,p2在第一象限时,
点P的横坐标为2+4=6,点P的,纵坐标坐标为6,
点P的坐标为(6,6);
③当四边形APOB是平行四边形时,p3在第三象限时,
,,
∴,,
即,,
解得:,,
此时点P的坐标为(-6,-6);
综上所述,存在满足条件的点P的坐标为(-2,6)或(6,6)或(-6,-6).
23.【答案】(1)解:把点、代入抛物线得,
,
解得,
∴抛物线的表达式为:;
(2)解:,
,
,
设直线的表达式为,
,,
∴,
解得,
∴直线的表达式为:,
把代入得:,
∴,
;
(3)解:如图,过点N作于点G,
过点,
,
,
∴直线BM的表达式为:,
,
设,,
∵四边形为矩形,
∴,,
又∵,
,
,,
,
,
、,
,,
.
一、选择题(每题3分,共30分)
1.二次函数中,自变量与函数的对应值如下表:
若,则下面叙述正确的是( )
A.该函数图象开口向上
B.该函数图象与轴的交点在轴的下方
C.对称轴是直线
D.若是方程的正数解,则
2.如图,二次函数的图象与x轴的交点为A、D的横坐标分别为3和,其图像与x轴围成封闭图形L,图形L内部(不包含边界)恰有4个整点(横纵坐标均为整数的点),系数a的值可以是( )
第2题图 第7题图
A. B. C. D.
3.定义:在平面直角坐标系中,若点A满足横、纵坐标都为整数,则把点A叫做“整点”.如:B(3,0)、C(﹣1,3)都是“整点”.抛物线y=ax2﹣2ax+a+2(a<0)与x轴交于点M,N两点,若该抛物线在M、N之间的部分与线段MN所围的区域(包括边界)恰有5个整点,则a的取值范围是( )
A.﹣1≤a<0 B.﹣2≤a<﹣1
C.﹣1≤a< D.﹣2≤a<0
4.已知二次函数的对称轴为,当时,y的取值范围是.则的值为( )
A.或 B.或 C. D.
5.函数图象与有交点,且满足,则的取值范围是( )
A. B.或2
C. D.或
6.设k为非负实数,且方程-2kx+4=0的两实数根为a,b,则+的最小值为( )
A.-7 B.-6 C.2 D.4
7.函数y=|ax2+bx|(a<0)的图象如图所示,下列说法正确的是( )
A.方程|ax2+bx|=k有四个不等的实数根
B.a+b>1
C.2a+b>0
D.5a+3b<1
8.已知二次函数()的图象如图所示,在下列5个结论:①;②;③;④;⑤(的实数),其中正确的结论有( )
第8题图 第10题图
A.1个 B.2个 C.3个 D.4个
9.将抛物线位于轴左侧的部分沿轴翻折,其余部分不变,翻折得到的图象和原来不变的部分构成一个新图象,若直线与新图象有且只有2个公共点,则的取值范围是( )
A. B.
C.或 D.或
10.如图,把二次函数的图象在x轴上方的部分沿着x轴翻折,得到的新函数叫做的“陷阱”函数.小明同学画出了的“陷阱”函数的图象,如图所示并写出了关于该函数的4个结论,其中正确结论的个数为( )
①图象具有对称性,对称轴是直线; ②由图象得,,;
③该“陷阱”函数与y轴交点坐标为;④的“陷阱”函数与的“陷阱”函数的图象是完全相同的.
A.1 B.2 C.3 D.4
二、填空题填空题(每题4分,共24分)
11. 关于的二次函数,在时有最大值6,则 .
12.如图,抛物线与x轴交于A、B两点,与y轴交于C点,P为抛物线对称轴上动点,则取最小值时,点P坐标是 .
第12题图 第15题图
13.已知,为x轴上两点,,为二次函数图象上两点,当时,二次函数y随x增大而减小,若,时,恒成立,则A、B两点的最大距离为 .
14.已知函数(是常数,),(是常数,),在同一平面直角坐标系中,若无论为何值,函数和的图象总有公共点,则的取值范围是 .
15.如图,在平面直角坐标系中,抛物线与轴的正半轴交于点.矩形的边在线段上,点C、D在抛物线上,则矩形周长的最大值为 .
16.已知抛物线y=ax2+bx+c(a,b,c是常数,a<0)经过点(2,0),且2
②若对任意的实数m,都有bm-b≥am2-a,则
③若抛物线经过点(-1,0),在抛物线上有且仅有2个点到x轴的距离等于n(n>0),则;
④点A(x1,y1),B(x2,y2)在抛物线上,且都在y轴右侧,若4a+c>0,则(x1-x2)(y1-y2)>0.
其中正确的是 (填写序号).
三、综合题(17-21每题6分,22、23每题8分,共46分)
17. 如图,△ABC中,,,,,反比例函数的图象与AB交于点,与BC交于点E.
(1)求m,k的值;
(2)点P为反比例函数图象上一动点(点P在D,E之间运动,不与D,E重合),过点P作,交y轴于点M,过点P作轴,交BC于点N,连接MN,求△PMN面积的最大值,并求出此时点P的坐标.
18.如图,对称轴为直线的抛物线与轴相交于,两点,其中点的坐标为,且点在抛物线上.
(1)求抛物线的解析式;
(2)点为抛物线与轴的交点;
①点在抛物线上,且,求点点坐标;
②设点是线段上的动点,作轴交抛物线于点,求线段长度的最大值.
19.如图,已知二次函数 的图象经过点 ,与 轴分别交于点 ,点 .点 是直线 上方的抛物线上一动点.
(1)求二次函数 的表达式;
(2)连接 , ,并把 沿 轴翻折,得到四边形 .若四边形 为菱形,请求出此时点 的坐标;
(3)当点 运动到什么位置时,四边形 的面积最大?求出此时 点的坐标和四边形 的最大面积.
20.如图,在平面直角坐标系中,已知抛物线y=ax2+bx+2与x轴相交于A(﹣1,0),B(4,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是直线BC上方抛物线上一动点,连接PB,PC,求△PBC面积的最大值以及此时点P的坐标;
(3)抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
21.如图1,已知抛物线与x轴交于点和点,与y轴交于点C.
(1)求b和c的值;
(2)已知点D是在第一象限内的抛物线上的一点,过点D作轴于点E.
①如图2,点D是抛物线的顶点,点P是上一点,若,求点P的坐标;
②如图3,若与交于点F,连接,且,求点D的坐标.
图1 图2 图3
22.如图,直线AB与抛物线交于、两点,与y轴交于点C,点D为线段AB上一点,连接OD、OB.
(1)求抛物线的解析式;
(2)若OD将分成面积相等的两部分,求点D的坐标;
(3)在平面坐标内是否存在点P,使得以A、O、B、P为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
23.如图1,在平面直角坐标中,抛物线与x轴交于点、两点,与y轴交于点C,连接,直线交y轴于点M.P为直线上方抛物线上一动点,过点P作x轴的垂线,分别交直线、于点E、F.
(1)求抛物线的表达式;
(2)当点P落在抛物线的对称轴上时,求的面积;
(3)若点N为y轴上一动点,当四边形为矩形时,求点N的坐标;
答案解析部分
1.【答案】D
【解答】根据表格可知
若,
A:该函数图象开口向上,叙述错误,图象开口应向下,不符合题意
B:该函数图象与轴的交点在轴的下方,叙述错误,函数图象与轴的交点在轴的上方,不符合题意
C:对称轴是直线,叙述错误,对称轴是直线,不符合题意
D:若是方程的正数解,则,叙述正确,当 时,,有,符合题意
故选:D
2.【答案】B
【解答】解:∵二次函数的图象与x轴的交点为A、D的横坐标分别为3和,
∴二次函数解析式为,对称轴为直线,
当时,,,
∴抛物线顶点坐标为,与y轴的交点坐标为,
如图所示:
∵图形L内部(不包含边界)恰有4个整点(横纵坐标均为整数的点),
∴,
解得,
∴四个选项中只有B选项符合题意,
故答案为:B
【解答】解:抛物线y=ax2﹣2ax+a+2(a<0)化为顶点式为y=a(x﹣1)2+2,故函数的对称轴:x=1,M和N两点关于x=1对称,根据题意,抛物线在M、N之间的部分与线段MN所围的区域(包括边界)恰有5个整点,这些整点是(0,0),(1,0),((1,1),(1,2),(2,0),
如图所示:
∵当x=0时,y=a+2
∴0≤a+2<1
当x=﹣1时,y=4a+2<0
即:,
解得﹣2≤a<﹣1
故选B.
4.【答案】D
【解答】解:∵二次函数的对称轴为,
∴,即,
∴,
当时,有最大值,
∴,
∴,
∴当时,随的增大而增大,
∴,,
解得:或;或;
经检验时,不符合题意;
∴,,
∴.
故答案为:D
5.【答案】D
【解答】解:如图,
函数 图象与函数有交点 ,且满足
对于函数,当x=1时,y=(1-m)2-5;当x=2时,y=(2-m)2-5;
对于函数,当x=1时,y=-4;当x=2时,y=-2;
若二次函数在对称轴右侧的部分与反比例函数有交点,且满足
从图中观察可得:
由①得:0≤m≤2
由②得:m≤2-3或m>2+3
∴0≤m≤2-3 ;
若二次函数在对称轴左侧的部分与反比例函数有交点,且满足
从图中观察可得:
由①得:m≤0或m≥2
由②得:2-3≤m≤2+3 ∴2≤m≤2+ 3 综上所述, 或
故答案为:D.
6.【答案】C
【解答】解:∵x2-2kx+4=0有两个实数根
∴ =(-2k)2-4×4=4k2-16≥0
∴k2≥4
∵k为非负实数
∴k≥2
由韦达定理得:a+b=2k,ab=4
∴(a-1)+(b-1)=2k-2,
(a-1)(b-1)=ab-(a+b)+1=4-2k+1=5-2k
∴(a-1)2+(b-1)2=[(a-1)+(b-1)]2-2(a-1)(b-1)=(2k-2)2-2(5-2k)=4(k-)2-7
令y=4(k-12)2-7,则函数图象开口向上,在对称轴右侧,y随k的增大而增大
∴当k=2时,y有最小值4(2-12)2-7=2,即 + 的最小值为2
故答案为:C.
7.【答案】D
【解答】解:A、由题意得当时,方程 |ax2+bx| =k没有实数根,故选项A错误;
B、由题意得时, ,当x=1时,,故选项B错误;
C、由题意得,∴,故选项C错误;
D、由题意得时, ,当时, ,
当x=1时,①,
当x=2时,,即②,
由①+②得 5a+3b<1
故答案为:D.
8.【答案】B
【解答】解∶开口向下,;对称轴在轴的右侧,a、b异号,则;抛物线与轴的交点在轴的上方,,则,所以①不正确;
当时图象在轴下方,则,即,所以②不正确;
对称轴为直线,则时图象在轴上方,则,所以③正确;
,则,而,则,所以④正确;
开口向下,当有最大值;
当时,,则,即,所以⑤正不确.
故答案为:B.
9.【答案】D
【解答】解: ,
令y=0,则x2+x-6=0,解得x=-3,y=2,
抛物线与x轴交点为(-3,0),(2,0),
由题意可得翻折后y轴左侧的抛物线为,
当直线经过点(0,-6) 时,得t=-6,此时直线与新图象有且只有2个公共点,
然后将直线向上平移过程中直至经过(0,6)之前,始终与新图象有且只有2个公共点,
把(0,6)代入中得t=6,
∴-6≤t<6时,直线与新图象有且只有2个公共点,
联立与,令y值相等,得=,
整理为2x2+3x+2t-12=0,
△=32+4×2(2t-12)=0,解得t=,
当t=,直线与新图象有且只有2个公共点,
∴或.
故答案为:D.
10.【答案】C
【解答】解:①∵二次函数的图象与x轴的交点为:,,
∴二次函数图象的对称轴为直线,故此说法正确;
②由函数图象可知,原二次函数的顶点坐标为,
∴该二次函数的解析式为:,
把代入得:,
解得:,
∴
,
∴,,,故原说法错误;
③把代入得:,
∴原函数与y轴的交点坐标为,
∵把二次函数的图象在x轴上方的部分沿着x轴翻折,得到的新函数叫做的“陷阱”函数,
∴该“陷阱”函数与y轴交点坐标为,故此说法正确;
④∵,
∴的图象与的图象关于x轴对称,
∴的“陷阱”函数与的“陷阱”函数的图象是完全相同,故此说法正确;
综上分析可知,正确的结论有3个,
故答案为:C
11.【答案】2或
【解答】解:y=ax2+a2,
①当a>0时,二次函数的对称轴为x=0,
∴x=-1时,ymax=a+a2=6,
解得:a=2或a=-3(舍去);
②当a<0时,二次函数的对称轴为x=0,
∴x=0时,ymax=a2=6,
解得:a=或a=(舍去),
综上所述,a=2或.
故答案为:2或.
12.【答案】
【解答】解:如图所示:连接BC,交抛物线对称轴于点P,根据的对称性可知,此时取得最小值,
令x=0,则y=2,
点C坐标为(0,2),
令y=0,则,
解得:
点B坐标为,
设直线BC的表达式为y=kx+b,
将点C坐标(0,2),点B坐标代入y=kx+b,
得:,
解得:,
直线BC的表达式为,
抛物线的对称轴,
点P的横坐标为,
把x=代入,
解得y=,
点P的坐标为 .
故答案为: .
13.【答案】8
【解答】解:当x=1时,y=3,
抛物线y=x2-mx+m+2的对称轴为直线,
∵当x<1时,二次函数y随x增大而减小,
,
∴m≥2.
∴m+1≥3,
当x=-2时,y=6+3m,当时,,
∵-2≤x1≤m+1,-2≤x2≤m+1,
∴|y1-y2|的最大值为,
∵|y1-y2|≤16恒成立,
.
∴-12≤m≤4,
∵m≥2,
∴2≤m≤4,
∴m的最大值为4,
∴A、B两点的最大距离为4-(-4)=8.
故答案为:8.
14.【答案】或
【解答】且 ,
该函数过点(-4,-2),
且 ,
该函数过(-5,0),(1,0)
当a<0时,无论k为何值,函数和的图象总有公共点,
a<0符合题意;
当a>0时,无论k为何值,函数和的图象总有公共点,
x=-4时,可得
解得
符合题意;
无论为何值,函数和的图象总有公共点,则的取值范围为或 .
15.【答案】13
【解答】设点D的横坐标为m,则点D的纵坐标为,
∴AD=,
∵抛物线的对称轴是直线,
∴点C的横坐标为3-(m-3)=6-m,
∴CD=2m-6,
∴矩形ABCD的周长=,
∴当m=5时,矩形周长有最大值为13,
故答案为:13.
16.【答案】①②③
【解答】解:①∵a<0, 2
∴方程ax2+bx+c=0有两个不相等的实数根 ,结论①正确;
②∵y=ax2+bx+c,经过点(2,0),∴4a+2b+c=0.
若对任意的实数m,都有bm-b≥am2-a ,即-am2+bm+a-b≥0总成立,
则,
∵总成立,
∴b-2a=0,b=2a.
∴4a+2b+c=8a+c=0,c=-8a.
∵2
∴,结论②正确;
③∵抛物线经过点(-1,0) 和 点(2,0)时,对称轴为,
∴4a+2b+c=0,a-b+c=0,
解得:a+b=0,
∴b=-a,
c=-a+b=-2a,
当时,抛物线有最大值
当 时,抛物线上有4个点到x轴的距离等于n;
当 时,抛物线上有3个点到x轴的距离等于n;
当 时,抛物线上有且仅有2个点到x轴的距离等于n;结论③正确;
④∵4a+2b+c=0,∴4a+c=-2b>0,∴b<0,
故对称轴,
∵a<0,∴抛物线开口向下,在对称轴右侧y随x的增大而减小.
∵点A(x1,y1),B(x2,y2)在抛物线上,且都在y轴右侧,
故x1
故答案为:①②③.
17.【答案】(1)解:,,.
又,.
,点.
设直线AB的函数表达式为,
将,代入,得
∴直线AB的函数表达式为.
将点代入,得.
.
将代入,得.
(2)解:延长NP交y轴于点Q,交AB于点L.
,,.
轴,,.
,,,.
设点P的坐标为,,则,.
.
.
当时,有最大值,此时.
18.【答案】(1)解:抛物线的对称轴为直线,
又点与在抛物线上,
,
解得,
抛物线的解析式为
(2)解:①由(1)知,二次函数的解析式为,
抛物线与轴的交点的坐标为,与轴的另一交点为,
则,,
设点坐标为,
,
,
,
则,
当时,,
当时,,
点的坐标为或;
②如图,
设直线的解析式为,
将,代入得,
解得,
直线的解析式为,
设点坐标为,,
则点坐标为,
,
当时,线段的长度有最大值.
19.【答案】(1)解:将点B和点C的坐标代入 ,
得 ,解得 , .
∴ 该二次函数的表达式为 .
(2)解:若四边形POP′C是菱形,则点P在线段CO的垂直平分线上;如图,连接PP′,则PE⊥CO,垂足为E,∵ C(0,3),∴ E(0, ),∴ 点P的纵坐标等于 .∴ ,解得 , (不合题意,舍去),
∴ 点P的坐标为( , ).
(3)解:过点P作y轴的平行线与BC交于点Q,与OB交于点F,设P(m, ),设直线BC的表达式为 ,则 , 解得 .
∴直线BC的表达式为 .
∴Q点的坐标为(m, ),
∴ .
当 ,
解得 ,∴ AO=1,AB=4,
∴ S四边形ABPC =S△ABC+S△CPQ+S△BPQ
=
=
当 时,四边形ABPC的面积最大.
此时P点的坐标为 ,四边形ABPC的面积的最大值为 .
20.【答案】(1)解:把A(﹣1,0),B(4,0)代入y=ax2+bx+2得:
,
解得,
∴抛物线的解析式为;
(2)解:过P作PK∥y轴交BC于K,如图:
在中,令x=0得y=2,
∴C(0,2),
由B(4,0),C(0,2)得直线BC解析式为,
设P(t,),则K,
∴PK=
∴S△PBC=,
∵﹣1<0,
∴当t=2时,S△PBC取最大值4,此时P(2,3),
∴△PBC面积的最大值为4,此时点P的坐标为(2,3);
(3)解:抛物线上存在点Q,使∠QCB=45°,理由如下:
当Q在BC上方时,过B作BT⊥CQ于T,过T作MN⊥y轴于N,过B作BM⊥MN于M,如图:
∵∠QCB=45°,
∴△BCT是等腰直角三角形,
∴∠BTC=90°,BT=CT,
∴∠CTN=90°﹣∠BTM=∠TBM,
∵∠M=∠TNC=90°,
∴△BTM≌△TCN(AAS),
∴BM=NT,TM=CN,
设T(m,n),则NT=m,BM=n,
∵B(4,0),C(0,2),
∴TM=MN﹣NT=4﹣m,CN=ON﹣OC=n﹣2,
∵BM=NT,TM=CN,
∴,
解得
∴T(3,3),
由C(0,2),T(3,3)得直线CT解析式为,
联立,
解得,
∴Q();
当Q在BC下方时,过B作BR⊥CQ于R,过R作SW⊥y轴于W,过B作BS⊥SW于S,如图:
同理可得△BSR≌△RWC(AAS),
∴BS=RW,RS=CW,
设R(p,q),
∴,
解得,
∴R(1,﹣1),
∴直线CR解析式为y=﹣3x+2,
联立,
解得 ,
∴Q(9,﹣25),
综上所述,Q的坐标为()或(9,﹣25).
21.【答案】(1)解:将点和点代入抛物线中,
得,
解得,
所以,;
故
(2)解:①由(1)知抛物线的表达式为
,抛物线的顶点D的坐标为
设点P的坐标为,
根据勾股定理,得,,
,
,
即,
解得.
点P的坐标为;
②设直线的函数表达式为
把点和点代入,
得,
解得
直线的函数表达式为
设点E的坐标为,则点,点
,
则,.
由,得
整理得,
解得,(不符合题意,舍去),
当时,
点D的坐标为.
22.【答案】(1)解:由题意可得,
,解得:,
∴抛物线的解析式为:;
(2)解:设直线AB的解析式为:,则
,解得:,
∴直线AB的解析式为:,
设点D的坐标为(m,m+4),
∵OD将△分成面积相等的两部分,即,
∴,解得:,
∴点D的坐标为(-1,3);
(3)解:存在;
设点P的坐标为(xp,yp),
①当四边形AOBP是平行四边形时,p1在第二象限时,
轴,,
∵B(2,6),
∴点P的坐标为(-2,6);
②当四边形AOPB是平行四边形时,p2在第一象限时,
点P的横坐标为2+4=6,点P的,纵坐标坐标为6,
点P的坐标为(6,6);
③当四边形APOB是平行四边形时,p3在第三象限时,
,,
∴,,
即,,
解得:,,
此时点P的坐标为(-6,-6);
综上所述,存在满足条件的点P的坐标为(-2,6)或(6,6)或(-6,-6).
23.【答案】(1)解:把点、代入抛物线得,
,
解得,
∴抛物线的表达式为:;
(2)解:,
,
,
设直线的表达式为,
,,
∴,
解得,
∴直线的表达式为:,
把代入得:,
∴,
;
(3)解:如图,过点N作于点G,
过点,
,
,
∴直线BM的表达式为:,
,
设,,
∵四边形为矩形,
∴,,
又∵,
,
,,
,
,
、,
,,
.
同课章节目录
