二次函数的图像3

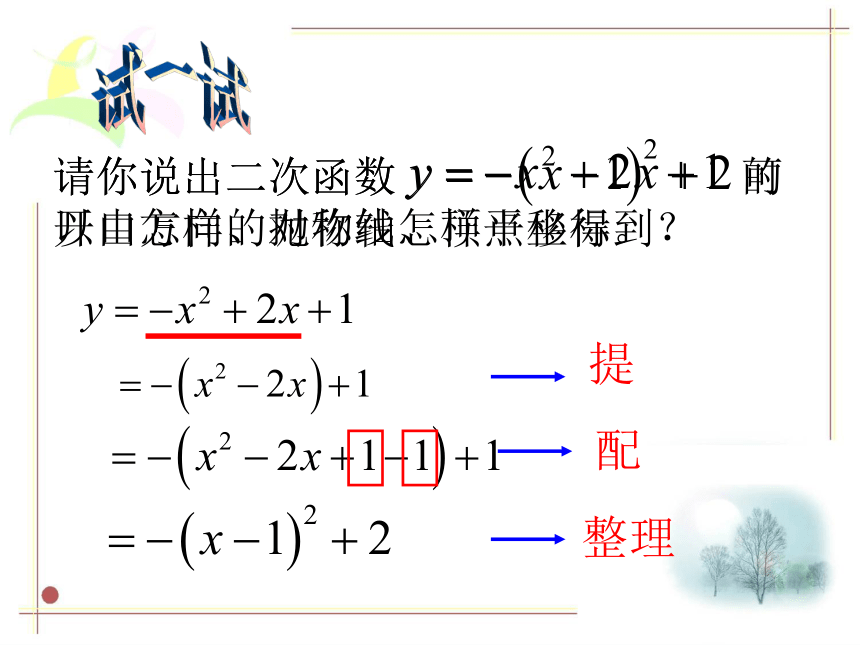
课件20张PPT。2.2 二次函数的图象（3）请你说出二次函数 的开口方向、对称轴、顶点坐标。试一试提配整理请你说出二次函数 可以由怎样的抛物线怎样平移得到？ 对于二次函数y=ax2+bx+c （ a≠0 ）的图象的形状、开口方向、顶点坐标又是怎样的？
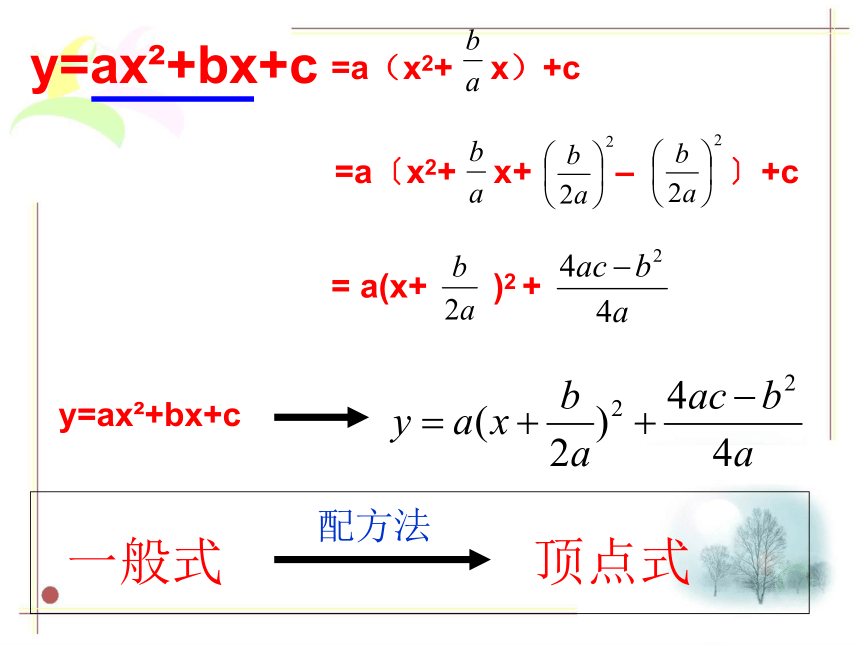
通过变形能否将y=ax2+bx+c转化为
y = a(x+m)2 +k的形式 ？y=ax2+bx+c =a（x2+ x）+c=a〔x2+ x+ – 〕+c= a(x+ )2 + y=ax2+bx+c 一般式顶点式配方法 二次函数 ( a≠0)的图象是一条抛物线，
顶点坐标是为（ ， ）
对称轴是直线x= y=ax2+bx+c当a>0时，抛物线的开口向上，顶点是抛物线上的最低点。当a<0时，抛物线的开口向下，顶点是抛物线上的最高点。例题学习:解：因此，抛物线的对称轴是直线x=3，顶点坐标是（3，2）。例4 求抛物线
的对称轴和顶点坐标。说出下列抛物线的开口方向、顶点坐标和对称轴：做一做:开口方向顶点坐标对称轴向下向上直线x=-1直线x=例5:已知二次函数y= x2+4x–3,
请回答下列问题：1、函数 的图象能否由函数
的图象通过平移变换得到？若能，请说出平移的过程，并画出示意图；2、说出函数图象的开口方向、对称轴和顶点坐标。1. 说出函数 的图象可由怎样的抛物线y=ax2（a≠0），经过怎样的平移后得到？课 内 练 习可以由抛物线 向左平移3个单
位，再向上平移21个单位得到。例：已知关于的二次函数的图象的顶点坐标为（-1，2），且图象过点（1，-3）
求这个二次函数的解析式；解：设这个二次函数的解析式为：这个二次函数的解析式为：把点（1，-3）代入 得， 2、请写出如图所示的抛物线的解析式： 课 内 练 习（0，1）（2，4）xyO解：设y = a(x-2)2+4把（0，1）代入y = a(x-2)2+4 得，1 = a(0-2)2+4y = (x-2)2+4a=
一座拱桥的示意图如图，当水面宽12m时，桥洞顶部
离水面4m。已知桥洞的拱形是抛物线，要求该抛物线
的函数解析式，你认为首先要做的工作是什么?1、点A 2、点B 3、抛物线的顶点C
所得的函数解析式相同吗？
请试一试。哪一种取法求
得的函数解析式最简单？ 探究活动:ABC4m12m 如果以
水平方向为x轴，取以下三个不同的点为坐标原点：　　大家收获不小吧！说说你的感受，让大家一起来分享，怎么样？你说我讲共交流我掌握了……
我学会了……
我体会到了……
我还有……疑问.见作业本作业：把抛物线 的图象向右平移3个单位，再向下平移2个单位，所得图象的解析式是 ，求b和c的值课 内 练 习3、已知抛物线 的图象如图所示，则a______0 b______0 c______0
2a+b______0
a+b+c______0
a-b+c______0
（填”>”=”<”） 01xy-1>><=>< 二次函数图象与系数a、b、c的关系:知识回顾:时，图象将发生怎样的变化？二次函数y=ax2y = a(x+m)2y = a(x+m)2 +k1、顶点坐标？（0，0）（–m，0）（ –m，k ）2、对称轴？y轴（直线x=0）（直线x= –m ）（直线x= –m ）3、平移问题？一般地，函数y=ax2的图象先向右（当m<0）或向左 （当m>0）平移|m|个单位可得y = a(x+m)2的图象；若再向上（当k>0 ）或向下 （当k<0 ）平移|k|个单位可得到y = a(x+m)2 +k的图象。
已知抛物线
（1）求它的顶点坐标；
（2）求它分别与x轴、y轴的交点坐标；
（3）利用图象写出当x为何值时，y>0若函数 的图象是以(3,-2)为顶点的抛物线,则p、q的值分别是__________.若抛物线 的顶点在x轴上,则m=______.若抛物线 关于y轴对称后的抛物线解析式是__________.ABC(6,4)(12,0)xy(6,-4)(-6,4)(-12,0)(-6,-4)ABC4m12m