二次函数的性质

课件14张PPT。2.3二次函数的性质实验初中 曹学勤问题：
次函数 ，当－1≤x≤2时， y的取值范围是什么？引入：请你来当回小老师－5≤y≤1y=2x－3一2二浩浩：将-1与2分别代入y=2x2-3，得y的值分别
是-1和5， 所以：－1≤y≤5浩浩的说法正确吗？填空：
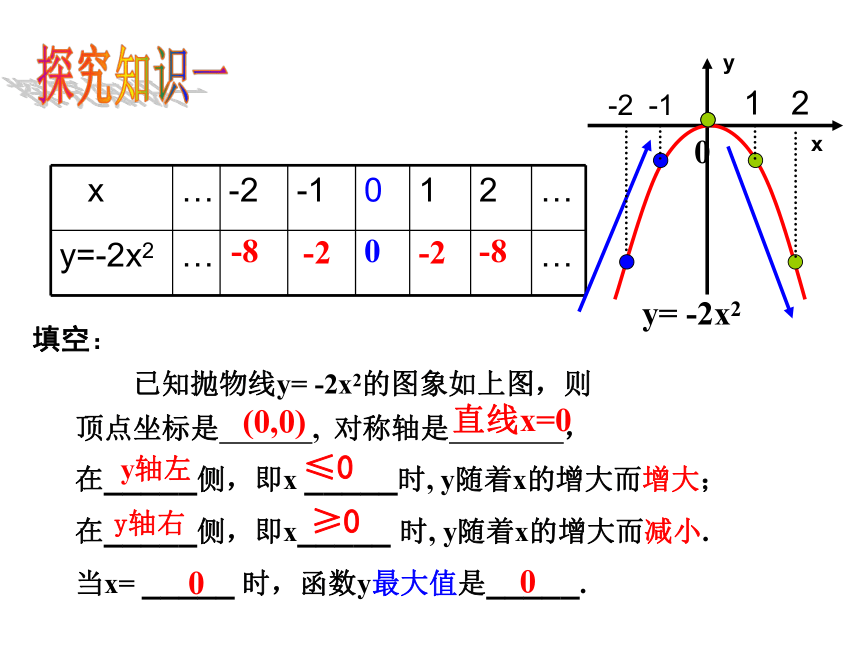
已知抛物线y= -2x2的图象如上图，则
　 顶点坐标是 , 对称轴是 ，
在_____侧，即x _____时, y随着x的增大而增大；
在_____侧，即x_____ 时, y随着x的增大而减小.
当x= _____ 时，函数y最大值是_____.
(0,0)直线x=0y轴右y轴左000y= -2x2≤0≥0yx探究知识一-8-20-2-8-2-112填空：
已知抛物线y= 2(x-1)2-2的图象如上图，则
　 顶点坐标是 , 对称轴是 ，
在 侧，即x 时, y随着x的增大而减小；
在 侧，即x 时, y随着x的增大而增大.
当x= 时，函数y最小值是____.
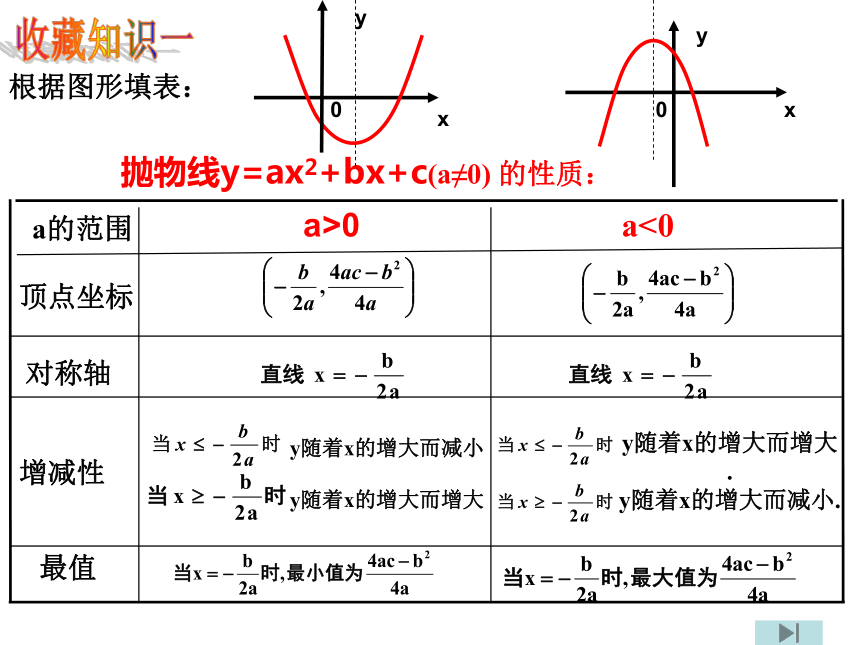
(1,-2)直线x=1对称轴右对称轴左-21 ≤1≥10y= 2(x-1)2-2yx探究知识一-21直线x=1a的范围顶点坐标对称轴增减性最值抛物线y=ax2+bx+c(a≠0) 的性质：y随着x的增大而减小
y随着x的增大而增大 y随着x的增大而增大
.
y随着x的增大而减小. 根据图形填表：收藏知识一a>0a<00xyyx0例题教学已知函数
（1）写出函数图象的对称轴与顶点坐标。
（2）自变量x在什么范围内时， y随着x的增大而增大？
何时y随着x的增大而减少；并求出函数的最大值或最小值。
（3）求图象与坐标轴的交点坐标。
（4）画出该函数图象的草图。 顶点（－1，2）直线x=－1当x≤－1时,y随着x的增大而增大；x≥－1时,y随着x的增大而减少当x=－1时，函数有最大值是2（－3，0）（1，0）变式：你能求出y=x2+2x+2与x轴的交点坐标吗？（0， ）例题教学已知函数
（1）写出函数图象的对称轴与顶点坐标。
（2）自变量x在什么范围内时， y随着x的增大而增大？
何时y随着x的增大而减少；并求出函数的最大值或最小值。
（3）求图象与坐标轴的交点坐标。
（4）画出该函数图象的草图。 顶点（－1，2）直线x=－1当x≤－1时,y随着x的增大而增大；x≥－1时,y随着x的增大而减少当x=－1时，函数有最大值是2（－3，0）（1，0）变式：你能求出y=x2+2x+2与x轴的交点坐标吗？（0， ）(1，0)(-3，0)(0，1.5)(-1，2)(-2,1.5)0xy画草图描出关键点
收藏知识三1.顶点3.与x轴交点2.与y轴交点4.与y轴交点的对称点抛物线y=ax2+bx+c(a ? 0)与x轴交点个数与一元二次方程ax2+bx+c=0 (a ? 0)的根的判别式b2-4ac关系。b2-4ac > 0b2-4ac = 0b2-4ac < 0知识收藏二00xy综合运用数形结合1．若抛物线y=kx2-2x+1与x轴有交点，则k的取值为 。k≤1且k≠0-26 2．根据图象填空
当x 时，y随x的增大而增大；
当x 时，y随x的增大而减小；
当x 时，y有最 值。
≥2≤2=2大 若函数y=－x2＋2x＋m的图象经过点A( ，y1)
B( ，y2)，
（1） 你能判断y1、y2的大小吗？ 　　( )

＞不能y1＜ y2＜y3温馨提示：通过该点与对称轴的距离的大小来作比较。C(－2，y3)（2）请将y1，y2，y3,用＜连接数形结合综合运用x1x23．变式：23y1 y2能若x1＜x2(2,5)
二次函数y=2x2-3，当－1≤x≤2时，y的取值范围是什么？揭晓-3≤y≤5！必须考虑顶点的位置
是否在已知的范围内。0x y(-1,-1)(0,-3)温馨提示：2-15谈谈你这节课的收获：三个收藏分享喜悦2．二次函数y=ax2+bx+c与x轴的交点坐标与
二次方程ax2+bx+c＝０的解关系。 1．二次函数y=ax2+bx+c（a≠0)的性质。本节课的几个数学思想的运用：
函数思想 方程思想 转化思想 数形结合思想3．用五点法画二次函数y=ax2+bx+c草图。课后作业：配套作业本数与形，
本是相倚依，
焉能分作两边飞。
数缺形时少直觉、形少数时难入微。
数形结合百般好，隔离分家万事非。
数学能锻炼你的思维;
数学让你变得更加聪明！教师寄语