浙教版数学九年级上册1.2 二次函数的图像 精品同步练习(含解析)
文档属性
| 名称 | 浙教版数学九年级上册1.2 二次函数的图像 精品同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版九年级上册数学 1.2 二次函数的图像 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.关于二次函数的下列结论,不正确的是( )
A.图象的开口向上 B.当时,随的增大而减小
C.图象经过点 D.图象的对称轴是直线
2.关于二次函数,下列说法正确的是( )
A.图像开口向下 B.图像经过点 C.图像的对称轴是直线 D.最小值是
3.已知,是抛物线上两点,则正数( )
A.2 B.4 C.8 D.16
4..已知函数经过A(m,)、B(m 1,),若.则m的取值范围是( )
A. B. C. D.
5.抛物线y=2x2, y=-2x2, y=x2的共同性质是( )
A.开口向上 B.对称轴是y轴 C.都有最高点 D.y随x的增大而增大
6.抛物线的顶点坐标是( )
A.(,1) B.(5,1) C.(,) D.(1,)
7.已知的图象如图所示,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.已知抛物线与二次函数y=-5x2的图象相同,开口方向相同,且顶点坐标为(-1,2020),它对应的函数表达式为( )
A.y=-5(x-1) 2+2020 B.y=5(x-1) 2+2020 C.y=5(x+1) 2+2020 D.y=-5(x+1)2+2020
9.有下列四个函数:①;②;③;④.其中图象经过如图所示阴影部分(包括边界)的函数有( )
A.①② B.①③ C.②③ D.②③④
10.如图,菱形对角线,相交于点,点,分别在线段,上,且.以为边作一个菱形,使得它的两条对角线分别在线段,上,设,新作菱形的面积为,则反映与之间函数关系的图象大致是( )
A.B.C.D.
填空题(本大题共5小题,每小题4分,共20分。)
11.二次函数y=﹣x2﹣2x+2的对称轴是x=__________.
12.若二次函数y=2x2﹣3的图象上有两个点A(﹣3,m)、B(2,n),则m_____n(填“<”或“=”或“>”).
13.若抛物线的顶点在第一象限,则m的取值范围为______.
14.一抛物线的形状,开口方向与相同,顶点在(-2,3),则此抛物线的解析式为_______.
15.二次函数y=x2﹣4x+m的最小值是2,则m=_____.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.已知点A(t,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)与y=x图象的交点.
(1)求t;
(2)若函数y=ax2+bx+4的图象与x轴只有一个交点,求a,b;
(3)若1≤a≤2,设当≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
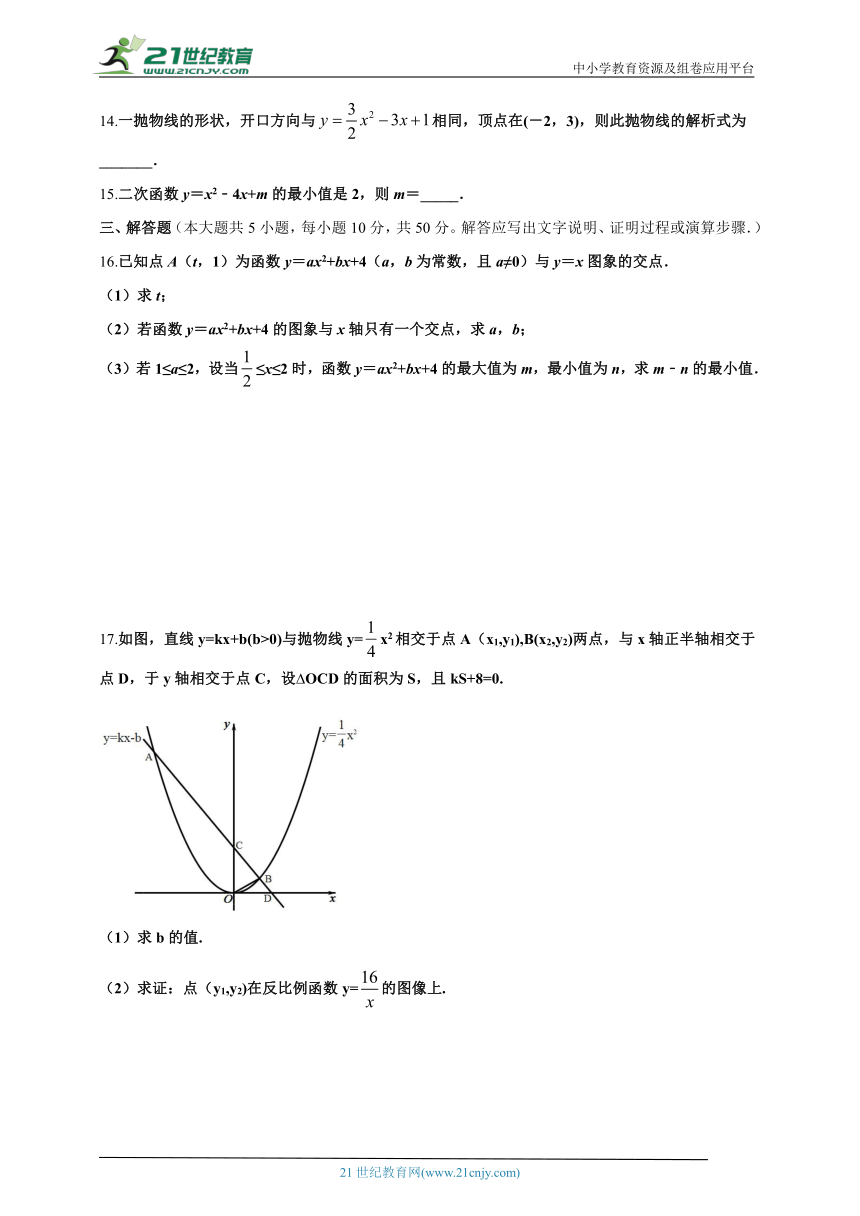
17.如图,直线y=kx+b(b>0)与抛物线y=x2相交于点A(x1,y1),B(x2,y2)两点,与x轴正半轴相交于点D,于y轴相交于点C,设 OCD的面积为S,且kS+8=0.
(1)求b的值.
(2)求证:点(y1,y2)在反比例函数y=的图像上.
18.一条抛物线的顶点和形状都与抛物线相同,但开口方向相反,求此抛物线解析式,并画出它的图像.
19.二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x … -4 -3 -2 -1 0 1 …
… 5 0 -3 -4 -3 m …
(1)m= ;
(2)在图中画出这个二次函数的图象;
(3)当时,x的取值范围是 ;
(4)当时,y的取值范围是 .
20.如图,在平面直角坐标系中,为原点,四边形是矩形,点、的坐标分别是和,点为对角线上一动点(不与、重合),连结,作,交轴于点,以线段、为邻边作矩形.
(1)填空:点的坐标为______;
(2)当是等腰三角形时,试求出的长;
(3)设,矩形的面积为,求关于的函数关系式,并求出的最小值.
浙教版九年级上册数学 1.2二次函数的图像 同步练习(解析版)
考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.关于二次函数的下列结论,不正确的是( )
A.图象的开口向上 B.当时,随的增大而减小
C.图象经过点 D.图象的对称轴是直线
【答案】D
【分析】
根据二次函数图象性质解题.
【详解】
二次函数,,二次函数开口向上,故A正确;
顶点坐标为,对称轴为,故D错误;
当时,随的增大而减小,故B正确;
当时,,经过点,故C正确,
故选:D.
2.关于二次函数,下列说法正确的是( )
A.图像开口向下 B.图像经过点 C.图像的对称轴是直线 D.最小值是
【答案】D
【分析】
根据二次函数的解析式得到它的图象和性质,选出正确选项.
【详解】
A选项错误,二次项系数大于0,开口向上;
B选项错误,把点代入函数解析式不成立;
C选项错误,对称轴是直线;
D选项正确.
故选:D.
3.已知,是抛物线上两点,则正数( )
A.2 B.4 C.8 D.16
【答案】C
【分析】
根据二次函数的对称性可得,代入二次函数解析式即可求解.
【详解】
解:∵,是抛物线上两点,
∴,
∴且n为正数,
解得,
故选:C.
4.已知函数经过A(m,)、B(m 1,),若.则m的取值范围是( )
A. B. C. D.
【答案】B
【分析】
由图像开口向下,对称轴为y=0知,要使,需使A点更靠近对称轴y轴,由此列出关于m的不等式解之即可 .
【详解】
解:∵图像开口向下,对称轴为y=0且
∴,下面解此不等式.
第一种情况,当m<0时,得,解得m<0;
第二种情况,当时,得,解得;
第三种情况,当时,得,解得,无解;
综上所述得.
故选:B.
5.抛物线y=2x2, y=-2x2, y=x2的共同性质是( )
A.开口向上 B.对称轴是y轴 C.都有最高点 D.y随x的增大而增大
【答案】B
【分析】
根据二次函数的图象与性质解题.
【详解】
抛物线y=2x2, y=x2 开口向上,对称轴是对称轴是y轴,有最低点,在y轴的右侧,y随x的增大而增大,y=-2x2,开口向下,对称轴是对称轴是y轴,有最高点,在y轴的左侧,y随x的增大而增大,
故抛物线y=2x2, y=-2x2, y=x2的共同性质是对称轴是y轴,
故选:B.
6..抛物线的顶点坐标是( )
A.(,1) B.(5,1) C.(,) D.(1,)
【答案】B
【分析】
根据二次函数的顶点求解即可.
【详解】
解:抛物线y=-(x-5)2+1的顶点坐标是(5,1),
故选:B.
7.已知的图象如图所示,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】C
【分析】
根据图像判断二次函数的系数a、b、c的正负性,即可求得.
【详解】
∵二次函数图像开口向下
∴a<0
又∵二次函数图形与y轴交点在y正半轴上
∴c>0
∵对称轴在y轴左侧
∴
∴b<0
∴ac<0,bc<0
∴点在第三象限
故选C
8.已知抛物线与二次函数y=-5x2的图象相同,开口方向相同,且顶点坐标为(-1,2020),它对应的函数表达式为( )
A.y=-5(x-1) 2+2020 B.y=5(x-1) 2+2020 C.y=5(x+1) 2+2020 D.y=-5(x+1)2+2020
【答案】D
【分析】
根据题意及二次函数的图像与性质可直接进行排除选项.
【详解】
由已知抛物线与二次函数y=-5x2的图象相同,开口方向相同,且顶点坐标为(-1,2020),则有该抛物线解析式为:y=-5(x+1)2+2020;
故选D.
9.有下列四个函数:①;②;③;④.其中图象经过如图所示阴影部分(包括边界)的函数有( )
A.①② B.①③ C.②③ D.②③④
【答案】D
【分析】
根据阴影部分顶点坐标,结合函数图像,作出判断即可.
【详解】
解:①;图像经过(0,0)、(1,2)两点,如图1
②;图像经过(0,4)、(3,2)两点,如图2
③;图像经过(1,4)、(4,1)两点,如图3
④;图像开口向下,顶点为,经过点,,如图4.
∴图象经过如图所示阴影部分(包括边界)的函数有②③④
故选:D.
10.如图,菱形对角线,相交于点,点,分别在线段,上,且.以为边作一个菱形,使得它的两条对角线分别在线段,上,设,新作菱形的面积为,则反映与之间函数关系的图象大致是( )
A.B.C.D.
【答案】C
【分析】
,即可求解.
【详解】
解:设OB=a,则OP=a-x,
则OQ=OPtan∠QPO=(a-x)tan∠QPO,
故
∵2tan∠QPO为大于0的常数,
故上述函数为开口向上的抛物线,且x=a时,y取得最大值0,
故选:C.
填空题(本大题共5小题,每小题4分,共20分。)
11.二次函数y=﹣x2﹣2x+2的对称轴是x=__________.
【答案】-1
【分析】
利用抛物线配方变为顶点式来解即可.
【详解】
解:∵二次函数y=﹣x2﹣2x+2=﹣(x+1)2+3,
∴该函数的对称轴是直线x=﹣1,
故答案为:﹣1.
12.若二次函数y=2x2﹣3的图象上有两个点A(﹣3,m)、B(2,n),则m_____n(填“<”或“=”或“>”).
【答案】>
【分析】
易得抛物线y=2x2﹣3的对称轴是y轴,然后即可确定点A(﹣3,m)关于y对称的点的坐标是(3,m),再根据抛物线的性质解答即可.
【详解】
解:∵抛物线y=2x2﹣3的对称轴是y轴,
∴点A(﹣3,m)关于y对称的点的坐标是(3,m),
∵当x>0时,y随着x的增大而增大,2<3,
∴m>n.
故答案为:>.
13.若抛物线的顶点在第一象限,则m的取值范围为______.
【答案】
【分析】
直接利用抛物线的顶点形式得出抛物线的顶点坐标,结合第一象限点的坐标特点列出不等式组解答即可.
【详解】
抛物线,
顶点坐标为,
顶点在第一象限,
且,
的取值范围为,
故答案为.
14.一抛物线的形状,开口方向与相同,顶点在(-2,3),则此抛物线的解析式为_______.
【答案】
【分析】
根据二次函数的图象与性质即可得.
【详解】
抛物线的顶点为
可设此抛物线的解析式为
又此抛物线的形状,开口方向与相同
则此抛物线的解析式为
故答案为:.
15.二次函数y=x2﹣4x+m的最小值是2,则m=_____.
【答案】6
【分析】
先把y=x2﹣4x+m配成顶点式得到y=(x﹣2)2+m﹣4,根据二次函数的性质得到当x=2时,y有最小值为m﹣4,根据题意得m﹣4=2,然后解方程即可.
【详解】
解:y=x2﹣4x+m=(x﹣2)2+m﹣4,
∵a=1>0,
∴当x=2时,y有最小值为m﹣4,
∴m﹣4=2,
∴m=6.
故答案为:6.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.已知点A(t,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)与y=x图象的交点.
(1)求t;
(2)若函数y=ax2+bx+4的图象与x轴只有一个交点,求a,b;
(3)若1≤a≤2,设当≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
【答案】(1)t=1;(2)或;(3)m﹣n的最小值
【分析】
(1)把A(t,1)代入y=x即可得到结论;
(2)根据题意得方程组,解方程组即可得到结论;
(3)把A(1,1)代入y=ax2+bx+4得,b= 3 a,得到y=ax2 (a+3)x+4的对称轴为直线x=,根据1≤a≤2,得到对称轴的取值范围≤x≤2,当x=时,得到m= ,当x=2时,得到n= ,即可得到结论.
【详解】
解:(1)把A(t,1)代入y=x得t=1;
(2)∵y=ax2+bx+4的图象与x轴只有一个交点,
∴,
∴或;
(3)把A(1,1)代入y=ax2+bx+4得,b=﹣3﹣a,
∴y=ax2﹣(a+3)x+4=a(x﹣)2﹣,
∴对称轴为直线x=,
∵1≤a≤2,
∴≤x=≤2,
∵≤x≤2,
∴当x=时,y=ax2+bx+4的最大值为m=﹣,
当x=2时,n=﹣,
∴m﹣n=,
∵1≤a≤2,
∴当a=2时,m﹣n的值最小,
即m﹣n的最小值.
17.如图,直线y=kx+b(b>0)与抛物线y=x2相交于点A(x1,y1),B(x2,y2)两点,与x轴正半轴相交于点D,于y轴相交于点C,设 OCD的面积为S,且kS+8=0.
(1)求b的值.
(2)求证:点(y1,y2)在反比例函数y=的图像上.
【答案】(1)b=4(b>0) ;(2)见解析
【分析】
(1)根据直线解析式求OC和OD长,依据面积公式代入即可得;
(2)联立方程,根据根与系数的关系即可证明.
【详解】
(1)∵D(0,b),C(-,0)
∴由题意得OD=b,OC= -
∴S=
∴k ()+8=0 ∴b=4(b>0)
(2)∵
∴
∴
∴
∴点(y1,y2)在反比例函数y=的图像上
18.一条抛物线的顶点和形状都与抛物线相同,但开口方向相反,求此抛物线解析式,并画出它的图像.
【答案】,图见解析.
【分析】
根据二次函数的图像性质直接求解即可.
【详解】
解:所求抛物线的顶点和形状与抛物线相同,但开口方向相反,
∴为的相反数,
解析式为
19.如图,在平面直角坐标系中,为原点,四边形是矩形,点、的坐标分别是和,点为对角线上一动点(不与、重合),连结,作,交轴于点,以线段、为邻边作矩形.
(1)填空:点的坐标为______;
(2)当是等腰三角形时,试求出的长;
(3)设,矩形的面积为,求关于的函数关系式,并求出的最小值.
【答案】(1);(2)满足条件的的长为2或;(3),有最小值.
【解析】
【分析】
(1)求出AB、BC的长即可解决问题;
(2)存在.连接BE,取BE的中点K,连接DK、KC.首先证明B、D、E、C四点共圆,可得∠DBC=∠DCE,∠EDC=∠EBC,由tan∠ACO=∠ACO=,推出∠ACO=30°,∠ACD=60°由△DEC是等腰三角形,观察图象可知,只有ED=EC,推出∠DBC=∠DCE=∠EDC=∠EBC=30°,推出∠DBC=∠BCD=60°,可得△DBC是等边三角形,推出DC=BC=2,由此即可解决问题;
(3)①由(2)可知,B、D、E、C四点共圆,推出∠DBC=∠DCE=30°,由此即可解决问题;
②作DH⊥AB于H.想办法用x表示BD、DE的长,构建二次函数即可解决问题;
解答
【详解】
(1)∵四边形是矩形,∴,,,∴.
(2)如图1,在中,.∵是等腰三角形,故有如下三种情况:
①若,则.
②若,过作于,则.在中,由,得,∵,∴.在中,,∴.
③若,则,∴,这与矛盾,∴.
综上所述,满足条件的的长为2或.
(3)如图2,连结,取的中点,连结、.
∵,∴,以为圆心,为直径作圆,则、、、四点在同一圆上,∴,∴.则.
如图3,作于.
在中,∵,,
∴,,
∴.
在中,,
∴,
∴矩形的面积,
即.
∵,∴时,有最小值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版九年级上册数学 1.2 二次函数的图像 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.关于二次函数的下列结论,不正确的是( )
A.图象的开口向上 B.当时,随的增大而减小
C.图象经过点 D.图象的对称轴是直线
2.关于二次函数,下列说法正确的是( )
A.图像开口向下 B.图像经过点 C.图像的对称轴是直线 D.最小值是
3.已知,是抛物线上两点,则正数( )
A.2 B.4 C.8 D.16
4..已知函数经过A(m,)、B(m 1,),若.则m的取值范围是( )
A. B. C. D.
5.抛物线y=2x2, y=-2x2, y=x2的共同性质是( )
A.开口向上 B.对称轴是y轴 C.都有最高点 D.y随x的增大而增大
6.抛物线的顶点坐标是( )
A.(,1) B.(5,1) C.(,) D.(1,)
7.已知的图象如图所示,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.已知抛物线与二次函数y=-5x2的图象相同,开口方向相同,且顶点坐标为(-1,2020),它对应的函数表达式为( )
A.y=-5(x-1) 2+2020 B.y=5(x-1) 2+2020 C.y=5(x+1) 2+2020 D.y=-5(x+1)2+2020
9.有下列四个函数:①;②;③;④.其中图象经过如图所示阴影部分(包括边界)的函数有( )
A.①② B.①③ C.②③ D.②③④
10.如图,菱形对角线,相交于点,点,分别在线段,上,且.以为边作一个菱形,使得它的两条对角线分别在线段,上,设,新作菱形的面积为,则反映与之间函数关系的图象大致是( )
A.B.C.D.
填空题(本大题共5小题,每小题4分,共20分。)
11.二次函数y=﹣x2﹣2x+2的对称轴是x=__________.
12.若二次函数y=2x2﹣3的图象上有两个点A(﹣3,m)、B(2,n),则m_____n(填“<”或“=”或“>”).
13.若抛物线的顶点在第一象限,则m的取值范围为______.
14.一抛物线的形状,开口方向与相同,顶点在(-2,3),则此抛物线的解析式为_______.
15.二次函数y=x2﹣4x+m的最小值是2,则m=_____.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.已知点A(t,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)与y=x图象的交点.
(1)求t;
(2)若函数y=ax2+bx+4的图象与x轴只有一个交点,求a,b;
(3)若1≤a≤2,设当≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
17.如图,直线y=kx+b(b>0)与抛物线y=x2相交于点A(x1,y1),B(x2,y2)两点,与x轴正半轴相交于点D,于y轴相交于点C,设 OCD的面积为S,且kS+8=0.
(1)求b的值.
(2)求证:点(y1,y2)在反比例函数y=的图像上.
18.一条抛物线的顶点和形状都与抛物线相同,但开口方向相反,求此抛物线解析式,并画出它的图像.
19.二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x … -4 -3 -2 -1 0 1 …
… 5 0 -3 -4 -3 m …
(1)m= ;
(2)在图中画出这个二次函数的图象;
(3)当时,x的取值范围是 ;
(4)当时,y的取值范围是 .
20.如图,在平面直角坐标系中,为原点,四边形是矩形,点、的坐标分别是和,点为对角线上一动点(不与、重合),连结,作,交轴于点,以线段、为邻边作矩形.
(1)填空:点的坐标为______;
(2)当是等腰三角形时,试求出的长;
(3)设,矩形的面积为,求关于的函数关系式,并求出的最小值.
浙教版九年级上册数学 1.2二次函数的图像 同步练习(解析版)
考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.关于二次函数的下列结论,不正确的是( )
A.图象的开口向上 B.当时,随的增大而减小
C.图象经过点 D.图象的对称轴是直线
【答案】D
【分析】
根据二次函数图象性质解题.
【详解】
二次函数,,二次函数开口向上,故A正确;
顶点坐标为,对称轴为,故D错误;
当时,随的增大而减小,故B正确;
当时,,经过点,故C正确,
故选:D.
2.关于二次函数,下列说法正确的是( )
A.图像开口向下 B.图像经过点 C.图像的对称轴是直线 D.最小值是
【答案】D
【分析】
根据二次函数的解析式得到它的图象和性质,选出正确选项.
【详解】
A选项错误,二次项系数大于0,开口向上;
B选项错误,把点代入函数解析式不成立;
C选项错误,对称轴是直线;
D选项正确.
故选:D.
3.已知,是抛物线上两点,则正数( )
A.2 B.4 C.8 D.16
【答案】C
【分析】
根据二次函数的对称性可得,代入二次函数解析式即可求解.
【详解】
解:∵,是抛物线上两点,
∴,
∴且n为正数,
解得,
故选:C.
4.已知函数经过A(m,)、B(m 1,),若.则m的取值范围是( )
A. B. C. D.
【答案】B
【分析】
由图像开口向下,对称轴为y=0知,要使,需使A点更靠近对称轴y轴,由此列出关于m的不等式解之即可 .
【详解】
解:∵图像开口向下,对称轴为y=0且
∴,下面解此不等式.
第一种情况,当m<0时,得,解得m<0;
第二种情况,当时,得,解得;
第三种情况,当时,得,解得,无解;
综上所述得.
故选:B.
5.抛物线y=2x2, y=-2x2, y=x2的共同性质是( )
A.开口向上 B.对称轴是y轴 C.都有最高点 D.y随x的增大而增大
【答案】B
【分析】
根据二次函数的图象与性质解题.
【详解】
抛物线y=2x2, y=x2 开口向上,对称轴是对称轴是y轴,有最低点,在y轴的右侧,y随x的增大而增大,y=-2x2,开口向下,对称轴是对称轴是y轴,有最高点,在y轴的左侧,y随x的增大而增大,
故抛物线y=2x2, y=-2x2, y=x2的共同性质是对称轴是y轴,
故选:B.
6..抛物线的顶点坐标是( )
A.(,1) B.(5,1) C.(,) D.(1,)
【答案】B
【分析】
根据二次函数的顶点求解即可.
【详解】
解:抛物线y=-(x-5)2+1的顶点坐标是(5,1),
故选:B.
7.已知的图象如图所示,则点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】C
【分析】
根据图像判断二次函数的系数a、b、c的正负性,即可求得.
【详解】
∵二次函数图像开口向下
∴a<0
又∵二次函数图形与y轴交点在y正半轴上
∴c>0
∵对称轴在y轴左侧
∴
∴b<0
∴ac<0,bc<0
∴点在第三象限
故选C
8.已知抛物线与二次函数y=-5x2的图象相同,开口方向相同,且顶点坐标为(-1,2020),它对应的函数表达式为( )
A.y=-5(x-1) 2+2020 B.y=5(x-1) 2+2020 C.y=5(x+1) 2+2020 D.y=-5(x+1)2+2020
【答案】D
【分析】
根据题意及二次函数的图像与性质可直接进行排除选项.
【详解】
由已知抛物线与二次函数y=-5x2的图象相同,开口方向相同,且顶点坐标为(-1,2020),则有该抛物线解析式为:y=-5(x+1)2+2020;
故选D.
9.有下列四个函数:①;②;③;④.其中图象经过如图所示阴影部分(包括边界)的函数有( )
A.①② B.①③ C.②③ D.②③④
【答案】D
【分析】
根据阴影部分顶点坐标,结合函数图像,作出判断即可.
【详解】
解:①;图像经过(0,0)、(1,2)两点,如图1
②;图像经过(0,4)、(3,2)两点,如图2
③;图像经过(1,4)、(4,1)两点,如图3
④;图像开口向下,顶点为,经过点,,如图4.
∴图象经过如图所示阴影部分(包括边界)的函数有②③④
故选:D.
10.如图,菱形对角线,相交于点,点,分别在线段,上,且.以为边作一个菱形,使得它的两条对角线分别在线段,上,设,新作菱形的面积为,则反映与之间函数关系的图象大致是( )
A.B.C.D.
【答案】C
【分析】
,即可求解.
【详解】
解:设OB=a,则OP=a-x,
则OQ=OPtan∠QPO=(a-x)tan∠QPO,
故
∵2tan∠QPO为大于0的常数,
故上述函数为开口向上的抛物线,且x=a时,y取得最大值0,
故选:C.
填空题(本大题共5小题,每小题4分,共20分。)
11.二次函数y=﹣x2﹣2x+2的对称轴是x=__________.
【答案】-1
【分析】
利用抛物线配方变为顶点式来解即可.
【详解】
解:∵二次函数y=﹣x2﹣2x+2=﹣(x+1)2+3,
∴该函数的对称轴是直线x=﹣1,
故答案为:﹣1.
12.若二次函数y=2x2﹣3的图象上有两个点A(﹣3,m)、B(2,n),则m_____n(填“<”或“=”或“>”).
【答案】>
【分析】
易得抛物线y=2x2﹣3的对称轴是y轴,然后即可确定点A(﹣3,m)关于y对称的点的坐标是(3,m),再根据抛物线的性质解答即可.
【详解】
解:∵抛物线y=2x2﹣3的对称轴是y轴,
∴点A(﹣3,m)关于y对称的点的坐标是(3,m),
∵当x>0时,y随着x的增大而增大,2<3,
∴m>n.
故答案为:>.
13.若抛物线的顶点在第一象限,则m的取值范围为______.
【答案】
【分析】
直接利用抛物线的顶点形式得出抛物线的顶点坐标,结合第一象限点的坐标特点列出不等式组解答即可.
【详解】
抛物线,
顶点坐标为,
顶点在第一象限,
且,
的取值范围为,
故答案为.
14.一抛物线的形状,开口方向与相同,顶点在(-2,3),则此抛物线的解析式为_______.
【答案】
【分析】
根据二次函数的图象与性质即可得.
【详解】
抛物线的顶点为
可设此抛物线的解析式为
又此抛物线的形状,开口方向与相同
则此抛物线的解析式为
故答案为:.
15.二次函数y=x2﹣4x+m的最小值是2,则m=_____.
【答案】6
【分析】
先把y=x2﹣4x+m配成顶点式得到y=(x﹣2)2+m﹣4,根据二次函数的性质得到当x=2时,y有最小值为m﹣4,根据题意得m﹣4=2,然后解方程即可.
【详解】
解:y=x2﹣4x+m=(x﹣2)2+m﹣4,
∵a=1>0,
∴当x=2时,y有最小值为m﹣4,
∴m﹣4=2,
∴m=6.
故答案为:6.
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.已知点A(t,1)为函数y=ax2+bx+4(a,b为常数,且a≠0)与y=x图象的交点.
(1)求t;
(2)若函数y=ax2+bx+4的图象与x轴只有一个交点,求a,b;
(3)若1≤a≤2,设当≤x≤2时,函数y=ax2+bx+4的最大值为m,最小值为n,求m﹣n的最小值.
【答案】(1)t=1;(2)或;(3)m﹣n的最小值
【分析】
(1)把A(t,1)代入y=x即可得到结论;
(2)根据题意得方程组,解方程组即可得到结论;
(3)把A(1,1)代入y=ax2+bx+4得,b= 3 a,得到y=ax2 (a+3)x+4的对称轴为直线x=,根据1≤a≤2,得到对称轴的取值范围≤x≤2,当x=时,得到m= ,当x=2时,得到n= ,即可得到结论.
【详解】
解:(1)把A(t,1)代入y=x得t=1;
(2)∵y=ax2+bx+4的图象与x轴只有一个交点,
∴,
∴或;
(3)把A(1,1)代入y=ax2+bx+4得,b=﹣3﹣a,
∴y=ax2﹣(a+3)x+4=a(x﹣)2﹣,
∴对称轴为直线x=,
∵1≤a≤2,
∴≤x=≤2,
∵≤x≤2,
∴当x=时,y=ax2+bx+4的最大值为m=﹣,
当x=2时,n=﹣,
∴m﹣n=,
∵1≤a≤2,
∴当a=2时,m﹣n的值最小,
即m﹣n的最小值.
17.如图,直线y=kx+b(b>0)与抛物线y=x2相交于点A(x1,y1),B(x2,y2)两点,与x轴正半轴相交于点D,于y轴相交于点C,设 OCD的面积为S,且kS+8=0.
(1)求b的值.
(2)求证:点(y1,y2)在反比例函数y=的图像上.
【答案】(1)b=4(b>0) ;(2)见解析
【分析】
(1)根据直线解析式求OC和OD长,依据面积公式代入即可得;
(2)联立方程,根据根与系数的关系即可证明.
【详解】
(1)∵D(0,b),C(-,0)
∴由题意得OD=b,OC= -
∴S=
∴k ()+8=0 ∴b=4(b>0)
(2)∵
∴
∴
∴
∴点(y1,y2)在反比例函数y=的图像上
18.一条抛物线的顶点和形状都与抛物线相同,但开口方向相反,求此抛物线解析式,并画出它的图像.
【答案】,图见解析.
【分析】
根据二次函数的图像性质直接求解即可.
【详解】
解:所求抛物线的顶点和形状与抛物线相同,但开口方向相反,
∴为的相反数,
解析式为
19.如图,在平面直角坐标系中,为原点,四边形是矩形,点、的坐标分别是和,点为对角线上一动点(不与、重合),连结,作,交轴于点,以线段、为邻边作矩形.
(1)填空:点的坐标为______;
(2)当是等腰三角形时,试求出的长;
(3)设,矩形的面积为,求关于的函数关系式,并求出的最小值.
【答案】(1);(2)满足条件的的长为2或;(3),有最小值.
【解析】
【分析】
(1)求出AB、BC的长即可解决问题;
(2)存在.连接BE,取BE的中点K,连接DK、KC.首先证明B、D、E、C四点共圆,可得∠DBC=∠DCE,∠EDC=∠EBC,由tan∠ACO=∠ACO=,推出∠ACO=30°,∠ACD=60°由△DEC是等腰三角形,观察图象可知,只有ED=EC,推出∠DBC=∠DCE=∠EDC=∠EBC=30°,推出∠DBC=∠BCD=60°,可得△DBC是等边三角形,推出DC=BC=2,由此即可解决问题;
(3)①由(2)可知,B、D、E、C四点共圆,推出∠DBC=∠DCE=30°,由此即可解决问题;
②作DH⊥AB于H.想办法用x表示BD、DE的长,构建二次函数即可解决问题;
解答
【详解】
(1)∵四边形是矩形,∴,,,∴.
(2)如图1,在中,.∵是等腰三角形,故有如下三种情况:
①若,则.
②若,过作于,则.在中,由,得,∵,∴.在中,,∴.
③若,则,∴,这与矛盾,∴.
综上所述,满足条件的的长为2或.
(3)如图2,连结,取的中点,连结、.
∵,∴,以为圆心,为直径作圆,则、、、四点在同一圆上,∴,∴.则.
如图3,作于.
在中,∵,,
∴,,
∴.
在中,,
∴,
∴矩形的面积,
即.
∵,∴时,有最小值.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
