浙教版数学八年级上册 第一章三角形的初步认识—第二章 特殊三角形综合复习(含答案)
文档属性
| 名称 | 浙教版数学八年级上册 第一章三角形的初步认识—第二章 特殊三角形综合复习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 377.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 09:00:45 | ||
图片预览

文档简介
浙教版数学八年级上册第一章-第二章
一、单选题
1.以下是回收、绿色包装、节水、低碳四个标志,其中是轴对称图形的是( )
A. B.
C. D.
2.下列是真命题的是( )
A.有一个角等于60°的三角形是等边三角形
B.在同一平面内,,则
C.同旁内角互补角
D.对顶角相等么?
3.下列长度的三根小木棒,不能摆成三角形的是( )
A.,, B.,,
C.,, D.,,
4.如图,两把相同的直尺的一边分别与射线重合,另一边相交于点P,则平分的依据是( )
A.在角的内部到角两边距离相等的点在这个角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.角平分线的性质
D.角是轴对称图形
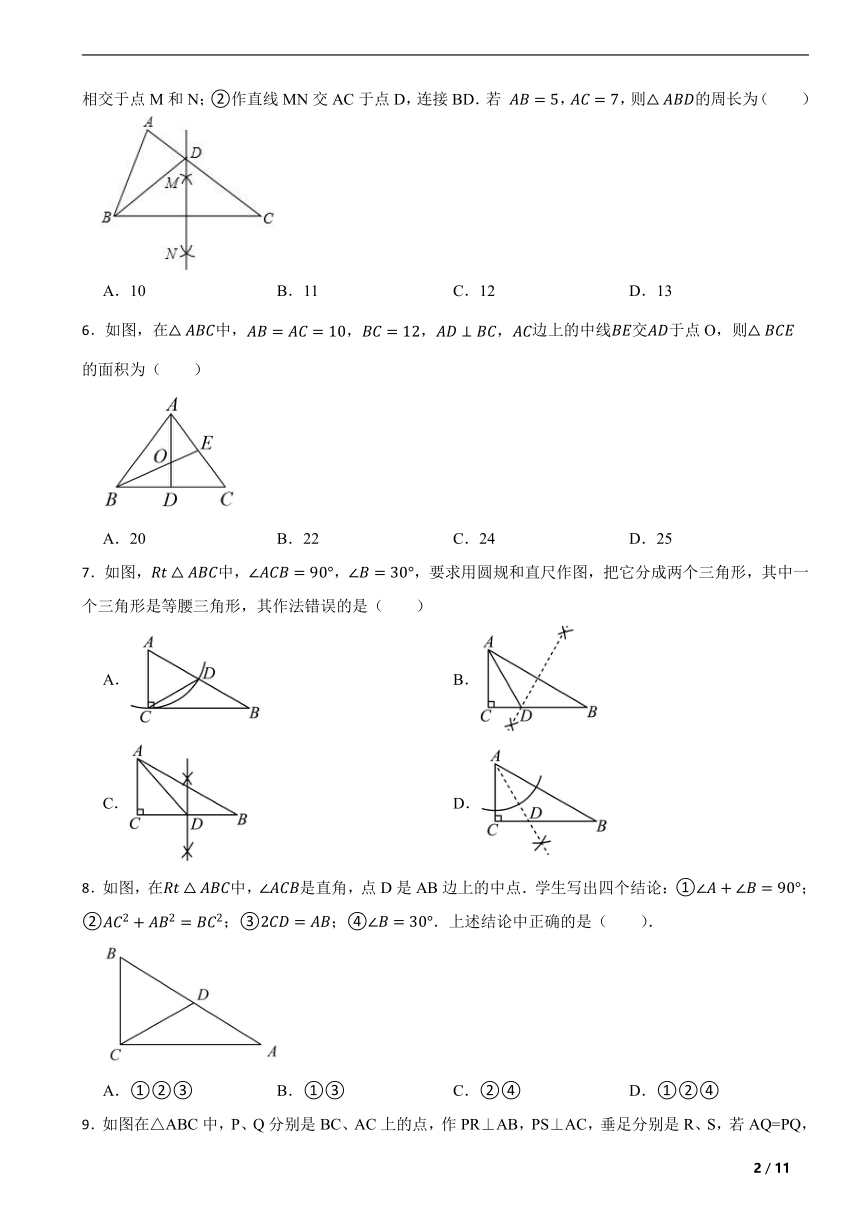
5.如图,在中,按以下步骤作图:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若 ,,则的周长为( )
A.10 B.11 C.12 D.13
6.如图,在中,边上的中线交于点O,则的面积为( )
A.20 B.22 C.24 D.25
7.如图,中,,,要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形,其作法错误的是( )
A. B.
C. D.
8.如图,在中,是直角,点D是AB边上的中点.学生写出四个结论:①;②;③;④.上述结论中正确的是( ).
A.①②③ B.①③ C.②④ D.①②④
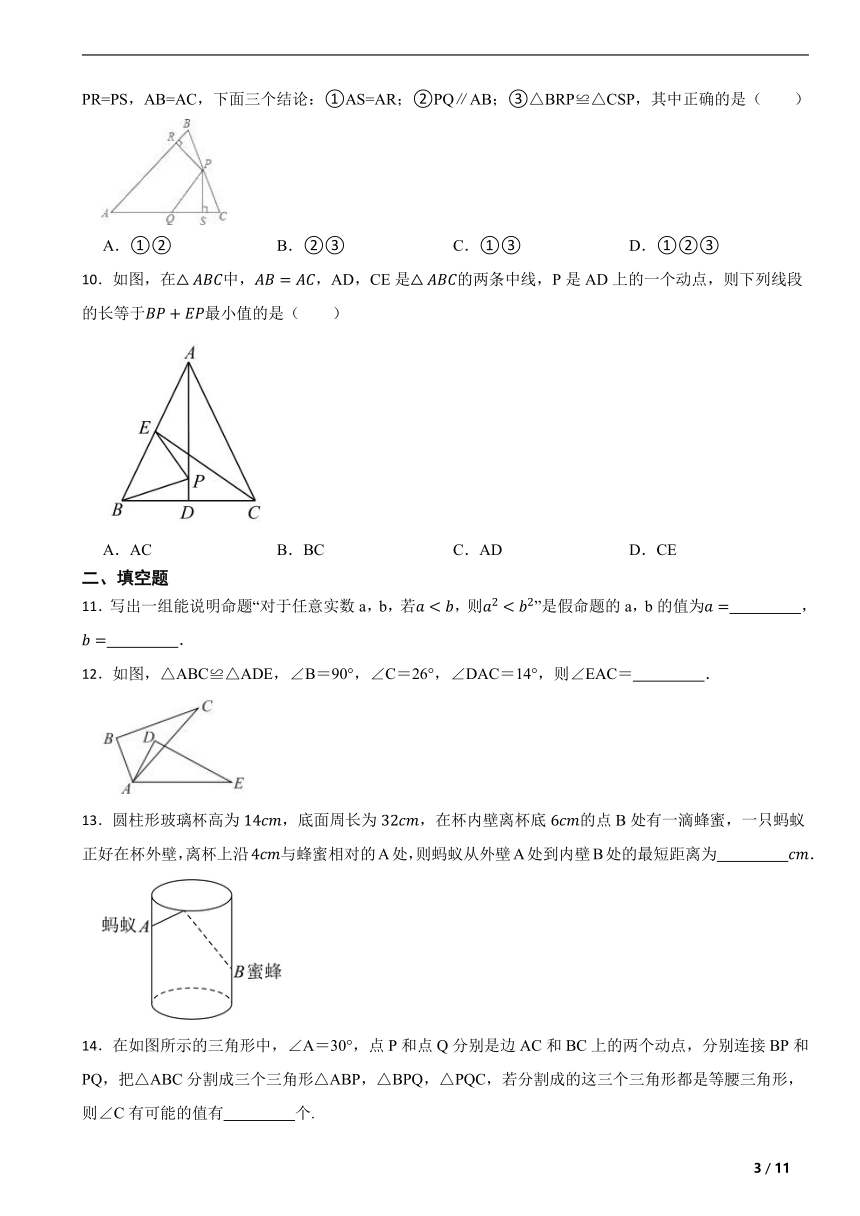
9.如图在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,AB=AC,下面三个结论:①AS=AR;②PQ∥AB;③△BRP≌△CSP,其中正确的是( )
A.①② B.②③ C.①③ D.①②③
10.如图,在中,,AD,CE是的两条中线,P是AD上的一个动点,则下列线段的长等于最小值的是( )
A.AC B.BC C.AD D.CE
二、填空题
11.写出一组能说明命题“对于任意实数a,b,若,则”是假命题的a,b的值为 , .
12.如图,△ABC≌△ADE,∠B=90°,∠C=26°,∠DAC=14°,则∠EAC= .
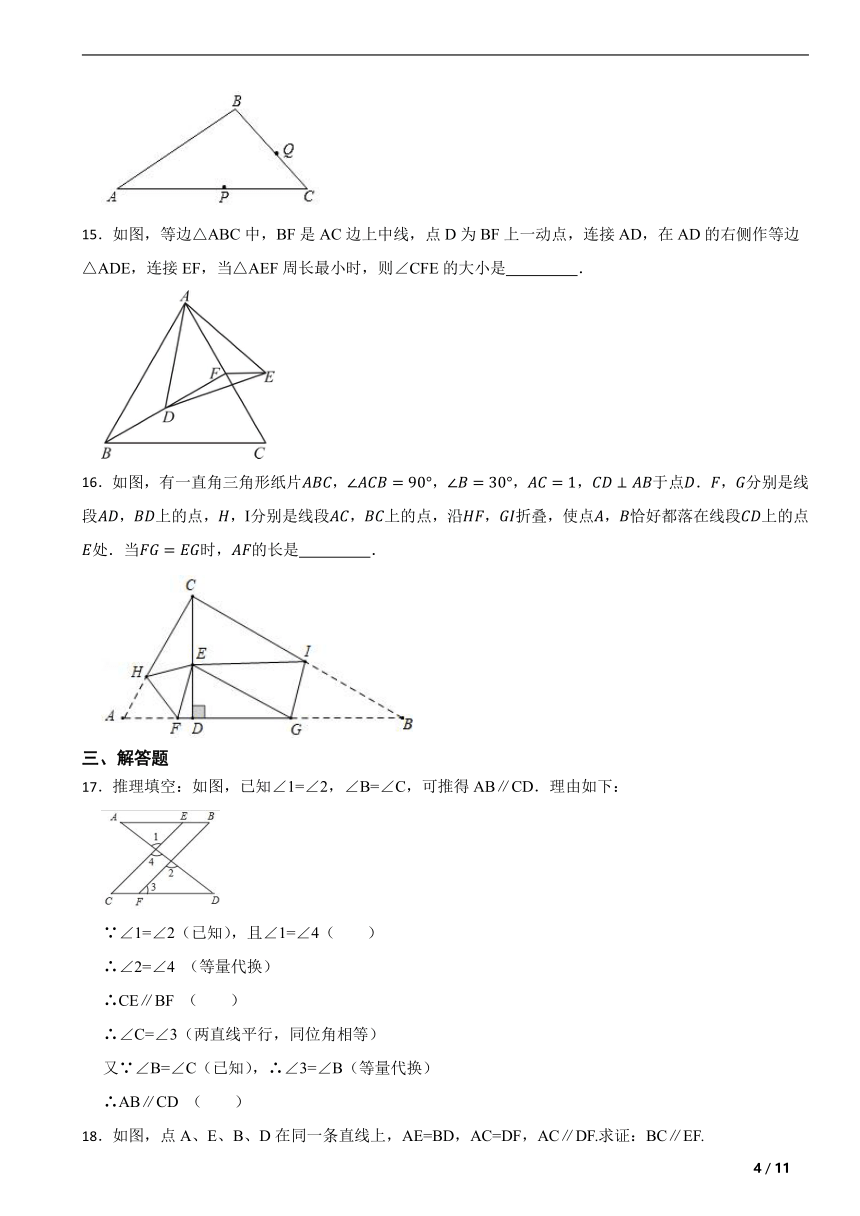
13.圆柱形玻璃杯高为,底面周长为,在杯内壁离杯底的点B处有一滴蜂蜜,一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的A处,则蚂蚁从外壁A处到内壁B处的最短距离为 .
14.在如图所示的三角形中,∠A=30°,点P和点Q分别是边AC和BC上的两个动点,分别连接BP和PQ,把△ABC分割成三个三角形△ABP,△BPQ,△PQC,若分割成的这三个三角形都是等腰三角形,则∠C有可能的值有 个.
15.如图,等边△ABC中,BF是AC边上中线,点D为BF上一动点,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,则∠CFE的大小是 .
16.如图,有一直角三角形纸片,,,,于点.,分别是线段,上的点,,Ⅰ分别是线段,上的点,沿,折叠,使点,恰好都落在线段上的点处.当时,的长是 .
三、解答题
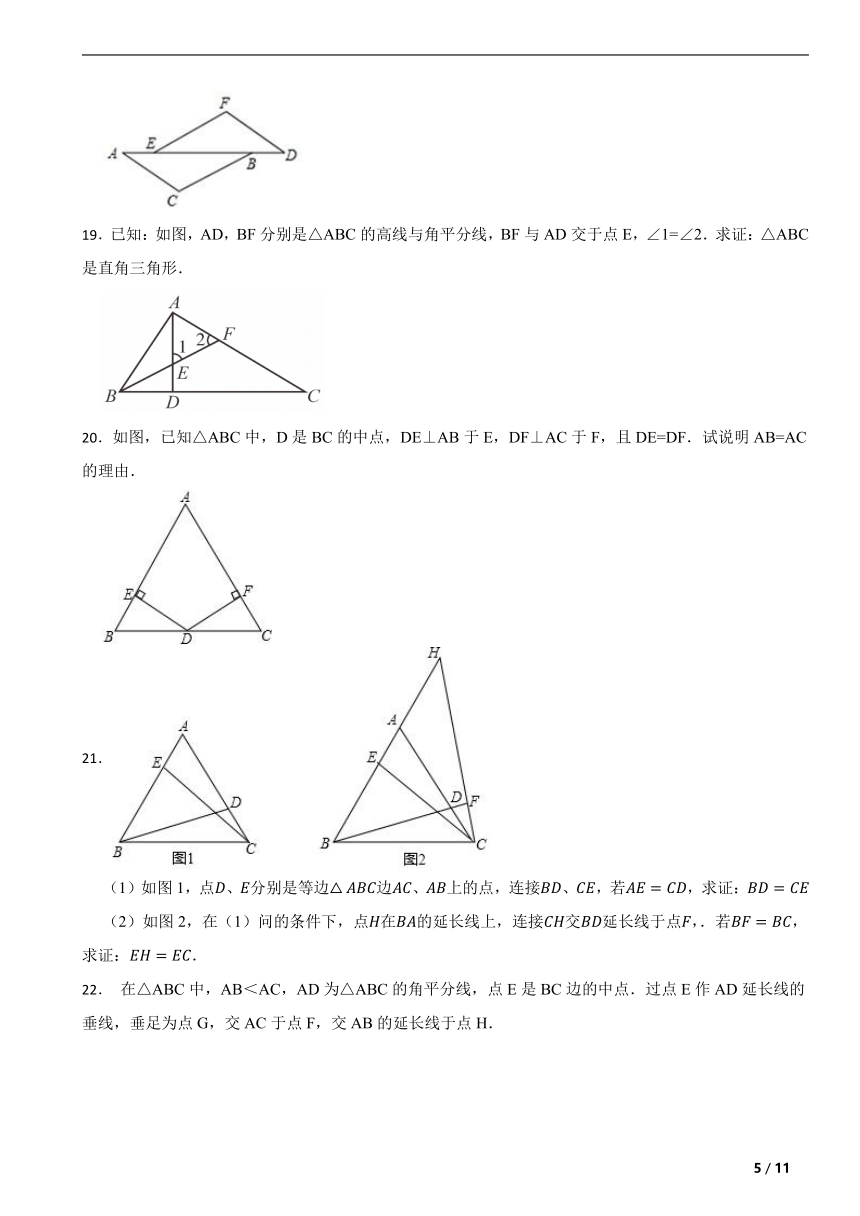
17.推理填空:如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠C=∠3(两直线平行,同位角相等)
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )
18.如图,点A、E、B、D在同一条直线上,AE=BD,AC=DF,AC∥DF.求证:BC∥EF.
19.已知:如图,AD,BF分别是△ABC的高线与角平分线,BF与AD交于点E,∠1=∠2.求证:△ABC是直角三角形.
20.如图,已知△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,且DE=DF.试说明AB=AC的理由.
21.
(1)如图1,点、分别是等边边、上的点,连接、,若,求证:
(2)如图2,在(1)问的条件下,点在的延长线上,连接交延长线于点,.若,求证:.
22. 在△ABC中,AB<AC,AD为△ABC的角平分线,点E是BC边的中点.过点E作AD延长线的垂线,垂足为点G,交AC于点F,交AB的延长线于点H.
(1)求证:∠AHF=∠AFH;
(2)探究:在线段EH上是否能找到一点P,使得△BEP≌△CEF.如果能够,请找出并证明之;
(3)证明:BH=CF.
23.如图,在四边形中,,交于点,交的延长线于点,点为的中点.
(1)求证:点也是的中点;
(2)若,且,,,求的长;
(3)在(2)的条件下,若线段上有一点,使得是等腰三角形,求的长.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】D
10.【答案】D
11.【答案】-2;-1
12.【答案】50°
13.【答案】20
14.【答案】4
15.【答案】
16.【答案】
17.【答案】解:∵∠1=∠2(已知),且∠1=∠4(对顶角相等)
∴∠2=∠4 (等量代换)
∴CE∥BF (同位角相等,两直线平行)
∴∠C=∠3(两直线平行,同位角相等)
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换)
∴AB∥CD (内错角相等,两直线平行)
故答案为:对顶角相等;同位角相等,两直线平行;内错角相等,两直线平行
18.【答案】证明:∵ , ,
∴
∵
∴
在 和 中
∴ ≌
∴
∴
19.【答案】解:由∵AD,BF 分别是 △ABC 的高线与角平分线,
∴∠ABF= ∠CBF,∠ADB= 90°,
∴∠CBF+∠BED=90°.
∵∠1=∠2=∠BED,
∴ ∠ABF+∠2=90°, 即∠BAC=90°,
∴ △ABC 是直角三角形.
20.【答案】解:∵DE⊥AB,DF⊥AC,
∴△DBE与△DCF是直角三角形.
∵在Rt△DBE与Rt△DCF中,,
∴Rt△DBE≌Rt△DCF(HL),
∴∠B=∠C,
∴AB=AC.
21.【答案】(1)证明:∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠ABC=∠BCA.
∴在△AEC和△CDB中
∴△AEC≌△CDB(SAS)
∴BD=CE.
(2)证明:如图:
由(1)△AEC≌△CDB,
∴∠ACE=∠CBD.
∴60°-∠ACE=60°-∠CBD,
即∠ABD=∠ECB.
∵BC=CF,
∴∠BCF=∠BFC,
又∵∠BCF=∠ECB+∠ECH,∠BFC=∠ABD+∠H,
∴∠ECH=∠H,
∴EH=EC.
22.【答案】(1)证明:∵AD为△ABC的角平分线,
∴∠HAG=∠FAG,
∵FH⊥AD,
∴∠AGH=∠AGF=90°,
在△AHG和△AFG中,
,
∴△AHG≌△AFG(ASA),
∴∠AHF=∠AFH.
(2)解:在线段EH上能找到一点P,使得△BEP≌△CEF,理由如下:
作BP∥AC,交EH于点P,则△BEP≌△CEF,
证明:∵点E是BC边的中点,
∴BE=CE,
∵BP∥AC,
∴∠EBP=∠C,
在△BEP和△CEF中,
,
∴△BEP≌△CEF(ASA);
(3)证明:∵△BEP≌△CEF,
∴BP=CF,
∵BP∥AC,
∴∠BPH=∠AFH,
∵∠AHF=∠AFH,
∴∠BPH=∠AHF,
∴BH=BP,
∴BH=CF.
23.【答案】(1)证明:,
,,
点为的中点,
,
在和中,,
,
,
点也是的中点;
(2)解:,,
,
在中,,
由(1)得:,
在中,;
(3)解:①当时,;
②当时,过点作于,如图1所示:
则,
,
即,
,
在中,,
;
③当时,如图2所示:
,
,
,,
,
,
,
;
综上所述,是等腰三角形,的长为4或或.
1 / 1
一、单选题
1.以下是回收、绿色包装、节水、低碳四个标志,其中是轴对称图形的是( )
A. B.
C. D.
2.下列是真命题的是( )
A.有一个角等于60°的三角形是等边三角形
B.在同一平面内,,则
C.同旁内角互补角
D.对顶角相等么?
3.下列长度的三根小木棒,不能摆成三角形的是( )
A.,, B.,,
C.,, D.,,
4.如图,两把相同的直尺的一边分别与射线重合,另一边相交于点P,则平分的依据是( )
A.在角的内部到角两边距离相等的点在这个角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.角平分线的性质
D.角是轴对称图形
5.如图,在中,按以下步骤作图:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若 ,,则的周长为( )
A.10 B.11 C.12 D.13
6.如图,在中,边上的中线交于点O,则的面积为( )
A.20 B.22 C.24 D.25
7.如图,中,,,要求用圆规和直尺作图,把它分成两个三角形,其中一个三角形是等腰三角形,其作法错误的是( )
A. B.
C. D.
8.如图,在中,是直角,点D是AB边上的中点.学生写出四个结论:①;②;③;④.上述结论中正确的是( ).
A.①②③ B.①③ C.②④ D.①②④
9.如图在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R、S,若AQ=PQ,PR=PS,AB=AC,下面三个结论:①AS=AR;②PQ∥AB;③△BRP≌△CSP,其中正确的是( )
A.①② B.②③ C.①③ D.①②③
10.如图,在中,,AD,CE是的两条中线,P是AD上的一个动点,则下列线段的长等于最小值的是( )
A.AC B.BC C.AD D.CE
二、填空题
11.写出一组能说明命题“对于任意实数a,b,若,则”是假命题的a,b的值为 , .
12.如图,△ABC≌△ADE,∠B=90°,∠C=26°,∠DAC=14°,则∠EAC= .
13.圆柱形玻璃杯高为,底面周长为,在杯内壁离杯底的点B处有一滴蜂蜜,一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的A处,则蚂蚁从外壁A处到内壁B处的最短距离为 .
14.在如图所示的三角形中,∠A=30°,点P和点Q分别是边AC和BC上的两个动点,分别连接BP和PQ,把△ABC分割成三个三角形△ABP,△BPQ,△PQC,若分割成的这三个三角形都是等腰三角形,则∠C有可能的值有 个.
15.如图,等边△ABC中,BF是AC边上中线,点D为BF上一动点,连接AD,在AD的右侧作等边△ADE,连接EF,当△AEF周长最小时,则∠CFE的大小是 .
16.如图,有一直角三角形纸片,,,,于点.,分别是线段,上的点,,Ⅰ分别是线段,上的点,沿,折叠,使点,恰好都落在线段上的点处.当时,的长是 .
三、解答题
17.推理填空:如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠C=∠3(两直线平行,同位角相等)
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )
18.如图,点A、E、B、D在同一条直线上,AE=BD,AC=DF,AC∥DF.求证:BC∥EF.
19.已知:如图,AD,BF分别是△ABC的高线与角平分线,BF与AD交于点E,∠1=∠2.求证:△ABC是直角三角形.
20.如图,已知△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于F,且DE=DF.试说明AB=AC的理由.
21.
(1)如图1,点、分别是等边边、上的点,连接、,若,求证:
(2)如图2,在(1)问的条件下,点在的延长线上,连接交延长线于点,.若,求证:.
22. 在△ABC中,AB<AC,AD为△ABC的角平分线,点E是BC边的中点.过点E作AD延长线的垂线,垂足为点G,交AC于点F,交AB的延长线于点H.
(1)求证:∠AHF=∠AFH;
(2)探究:在线段EH上是否能找到一点P,使得△BEP≌△CEF.如果能够,请找出并证明之;
(3)证明:BH=CF.
23.如图,在四边形中,,交于点,交的延长线于点,点为的中点.
(1)求证:点也是的中点;
(2)若,且,,,求的长;
(3)在(2)的条件下,若线段上有一点,使得是等腰三角形,求的长.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】B
9.【答案】D
10.【答案】D
11.【答案】-2;-1
12.【答案】50°
13.【答案】20
14.【答案】4
15.【答案】
16.【答案】
17.【答案】解:∵∠1=∠2(已知),且∠1=∠4(对顶角相等)
∴∠2=∠4 (等量代换)
∴CE∥BF (同位角相等,两直线平行)
∴∠C=∠3(两直线平行,同位角相等)
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换)
∴AB∥CD (内错角相等,两直线平行)
故答案为:对顶角相等;同位角相等,两直线平行;内错角相等,两直线平行
18.【答案】证明:∵ , ,
∴
∵
∴
在 和 中
∴ ≌
∴
∴
19.【答案】解:由∵AD,BF 分别是 △ABC 的高线与角平分线,
∴∠ABF= ∠CBF,∠ADB= 90°,
∴∠CBF+∠BED=90°.
∵∠1=∠2=∠BED,
∴ ∠ABF+∠2=90°, 即∠BAC=90°,
∴ △ABC 是直角三角形.
20.【答案】解:∵DE⊥AB,DF⊥AC,
∴△DBE与△DCF是直角三角形.
∵在Rt△DBE与Rt△DCF中,,
∴Rt△DBE≌Rt△DCF(HL),
∴∠B=∠C,
∴AB=AC.
21.【答案】(1)证明:∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠ABC=∠BCA.
∴在△AEC和△CDB中
∴△AEC≌△CDB(SAS)
∴BD=CE.
(2)证明:如图:
由(1)△AEC≌△CDB,
∴∠ACE=∠CBD.
∴60°-∠ACE=60°-∠CBD,
即∠ABD=∠ECB.
∵BC=CF,
∴∠BCF=∠BFC,
又∵∠BCF=∠ECB+∠ECH,∠BFC=∠ABD+∠H,
∴∠ECH=∠H,
∴EH=EC.
22.【答案】(1)证明:∵AD为△ABC的角平分线,
∴∠HAG=∠FAG,
∵FH⊥AD,
∴∠AGH=∠AGF=90°,
在△AHG和△AFG中,
,
∴△AHG≌△AFG(ASA),
∴∠AHF=∠AFH.
(2)解:在线段EH上能找到一点P,使得△BEP≌△CEF,理由如下:
作BP∥AC,交EH于点P,则△BEP≌△CEF,
证明:∵点E是BC边的中点,
∴BE=CE,
∵BP∥AC,
∴∠EBP=∠C,
在△BEP和△CEF中,
,
∴△BEP≌△CEF(ASA);
(3)证明:∵△BEP≌△CEF,
∴BP=CF,
∵BP∥AC,
∴∠BPH=∠AFH,
∵∠AHF=∠AFH,
∴∠BPH=∠AHF,
∴BH=BP,
∴BH=CF.
23.【答案】(1)证明:,
,,
点为的中点,
,
在和中,,
,
,
点也是的中点;
(2)解:,,
,
在中,,
由(1)得:,
在中,;
(3)解:①当时,;
②当时,过点作于,如图1所示:
则,
,
即,
,
在中,,
;
③当时,如图2所示:
,
,
,,
,
,
,
;
综上所述,是等腰三角形,的长为4或或.
1 / 1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
