1.1 认识三角形(2)同步练习2024-2025学年浙教版数学八年级上册(无答案)
文档属性
| 名称 | 1.1 认识三角形(2)同步练习2024-2025学年浙教版数学八年级上册(无答案) | 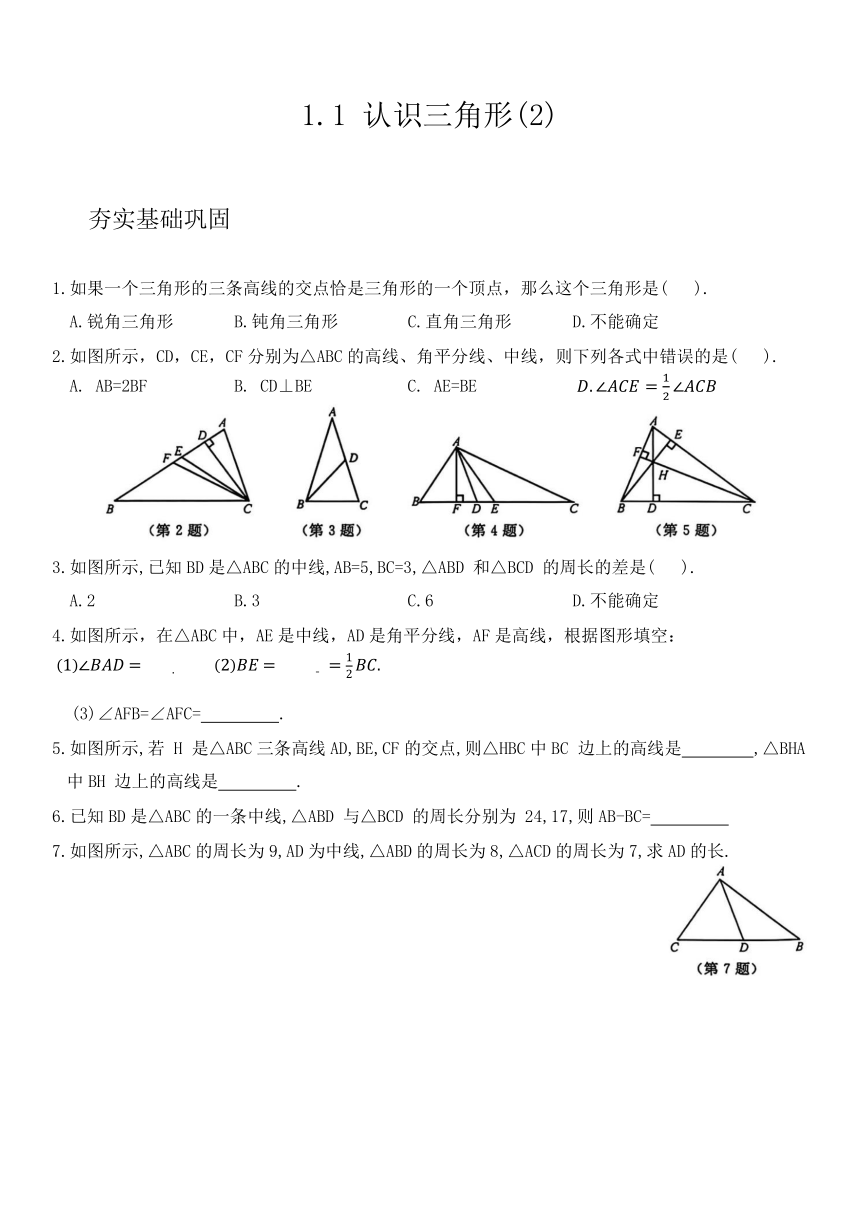 | |
| 格式 | docx | ||
| 文件大小 | 338.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-23 21:56:26 | ||
图片预览

文档简介
1.1 认识三角形(2)
夯实基础巩固
1.如果一个三角形的三条高线的交点恰是三角形的一个顶点,那么这个三角形是( ).
A.锐角三角形 B.钝角三角形 C.直角三角形 D.不能确定
2.如图所示,CD,CE,CF分别为△ABC的高线、角平分线、中线,则下列各式中错误的是( ).
A. AB=2BF B. CD⊥BE C. AE=BE
3.如图所示,已知BD是△ABC的中线,AB=5,BC=3,△ABD 和△BCD 的周长的差是( ).
A.2 B.3 C.6 D.不能确定
4.如图所示,在△ABC中,AE是中线,AD是角平分线,AF是高线,根据图形填空:
(3)∠AFB=∠AFC= .
5.如图所示,若 H 是△ABC三条高线AD,BE,CF的交点,则△HBC中BC 边上的高线是 ,△BHA中BH 边上的高线是 .
6.已知BD是△ABC的一条中线,△ABD 与△BCD 的周长分别为 24,17,则AB-BC=
7.如图所示,△ABC的周长为9,AD为中线,△ABD的周长为8,△ACD的周长为7,求AD的长.
8.如图所示,AD,CE是△ABC的两条高线, ,求AD的长.
能力提升培优
9.如图所示,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别为 D,C,F.下列说法中错误的是( ).
A.△ABC中,AD 是边BC上的高线
B.△ABC中,GC 是边BC 上的高线
C.△GBC中,GC是边BC 上的高线
D.△GBC中,CF 是边 BG 上的高线
10.如图所示,AD,BE,CF 依次为△ABC的高线、中线和角平分线.下列式子中错误的是( ),
A. AE=CE B.∠ADC=90° C.∠CAD=∠CBE D.∠ACB=2∠ACF
11.如图所示,AD,BE 是△ABC 的中线,给出下列结论:①S△AOE =S△COE;②S△OOB=S四边形EODC;③S△BOC=2S△BCE;④S△ABC=4S△BOC.其中正确的有( ).
A.1 个 B.2个 C.3个 D.4 个
12.如图所示,在△ABC中,AD为中线,DE⊥AB于点E,DF⊥AC于点F,AB=3,AC=4,DF=1.5,则DE= .
13.如图所示,在△ABC中,点D,E,F 分别在三边上,E是AC 的中点,AD,BE,CF 交于一点G,BD=2DC,S△GCD=3,S△BGD=4,则△ABC的面积是 .
14.在△ABC中,AB:AC=3:2,BC=AC+1.若△ABC的中线BD把△ABC的周长分成的两部分的比是8: 7,求边AB,AC的长.
15.已知在△ABC中,∠A=45°,高线 BD和高线CE 所在的直线交于点 H,求∠BHC的度数.
中考实战演练
16.如图所示,在△ABC中,AC边上的高线是( ).
A.线段 DA B.线段 BA C.线段 BC D.线段 BD
17.如图所示,在△ABC中,∠1=∠2,G为AD 中点,延长BG交AC 于点E,且BE⊥AC,F为AB上一点,且CF⊥AD 于点 H,下列判断:①线段 AD 是△ABE 的角平分线;②△ABG与△DBG 的面积相等;③线段 AE 是△ABG 的边 BG 上的高线;④∠1+∠FBC+∠FCB=90°.其中正确的有( ).
A.4个 B.3个 C.2个 D.1个
开放应用探究
18.如图所示,某市有三个车站A,B,C成三角形,一辆公共汽车从 B 站前往C 站.
(1)当汽车行驶到点D时,刚好 BD=CD,连结线段AD,AD是什么线段 这样的线段在△ABC中有几条呢 此时有面积相等的三角形吗
(2)汽车继续向前行驶,当行驶到点 E时,发现∠BAE=∠CAE,则AE 是什么线段 这样的线段在△ABC中有几条呢
(3)汽车继续向前行驶,当行驶到点 F时,发现∠AFB=∠AFC=90°,则AF是什么线段 这样的线段在△ABC中又有几条呢
夯实基础巩固
1.如果一个三角形的三条高线的交点恰是三角形的一个顶点,那么这个三角形是( ).
A.锐角三角形 B.钝角三角形 C.直角三角形 D.不能确定
2.如图所示,CD,CE,CF分别为△ABC的高线、角平分线、中线,则下列各式中错误的是( ).
A. AB=2BF B. CD⊥BE C. AE=BE
3.如图所示,已知BD是△ABC的中线,AB=5,BC=3,△ABD 和△BCD 的周长的差是( ).
A.2 B.3 C.6 D.不能确定
4.如图所示,在△ABC中,AE是中线,AD是角平分线,AF是高线,根据图形填空:
(3)∠AFB=∠AFC= .
5.如图所示,若 H 是△ABC三条高线AD,BE,CF的交点,则△HBC中BC 边上的高线是 ,△BHA中BH 边上的高线是 .
6.已知BD是△ABC的一条中线,△ABD 与△BCD 的周长分别为 24,17,则AB-BC=
7.如图所示,△ABC的周长为9,AD为中线,△ABD的周长为8,△ACD的周长为7,求AD的长.
8.如图所示,AD,CE是△ABC的两条高线, ,求AD的长.
能力提升培优
9.如图所示,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别为 D,C,F.下列说法中错误的是( ).
A.△ABC中,AD 是边BC上的高线
B.△ABC中,GC 是边BC 上的高线
C.△GBC中,GC是边BC 上的高线
D.△GBC中,CF 是边 BG 上的高线
10.如图所示,AD,BE,CF 依次为△ABC的高线、中线和角平分线.下列式子中错误的是( ),
A. AE=CE B.∠ADC=90° C.∠CAD=∠CBE D.∠ACB=2∠ACF
11.如图所示,AD,BE 是△ABC 的中线,给出下列结论:①S△AOE =S△COE;②S△OOB=S四边形EODC;③S△BOC=2S△BCE;④S△ABC=4S△BOC.其中正确的有( ).
A.1 个 B.2个 C.3个 D.4 个
12.如图所示,在△ABC中,AD为中线,DE⊥AB于点E,DF⊥AC于点F,AB=3,AC=4,DF=1.5,则DE= .
13.如图所示,在△ABC中,点D,E,F 分别在三边上,E是AC 的中点,AD,BE,CF 交于一点G,BD=2DC,S△GCD=3,S△BGD=4,则△ABC的面积是 .
14.在△ABC中,AB:AC=3:2,BC=AC+1.若△ABC的中线BD把△ABC的周长分成的两部分的比是8: 7,求边AB,AC的长.
15.已知在△ABC中,∠A=45°,高线 BD和高线CE 所在的直线交于点 H,求∠BHC的度数.
中考实战演练
16.如图所示,在△ABC中,AC边上的高线是( ).
A.线段 DA B.线段 BA C.线段 BC D.线段 BD
17.如图所示,在△ABC中,∠1=∠2,G为AD 中点,延长BG交AC 于点E,且BE⊥AC,F为AB上一点,且CF⊥AD 于点 H,下列判断:①线段 AD 是△ABE 的角平分线;②△ABG与△DBG 的面积相等;③线段 AE 是△ABG 的边 BG 上的高线;④∠1+∠FBC+∠FCB=90°.其中正确的有( ).
A.4个 B.3个 C.2个 D.1个
开放应用探究
18.如图所示,某市有三个车站A,B,C成三角形,一辆公共汽车从 B 站前往C 站.
(1)当汽车行驶到点D时,刚好 BD=CD,连结线段AD,AD是什么线段 这样的线段在△ABC中有几条呢 此时有面积相等的三角形吗
(2)汽车继续向前行驶,当行驶到点 E时,发现∠BAE=∠CAE,则AE 是什么线段 这样的线段在△ABC中有几条呢
(3)汽车继续向前行驶,当行驶到点 F时,发现∠AFB=∠AFC=90°,则AF是什么线段 这样的线段在△ABC中又有几条呢
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
