浙教版数学九年级上册3.8弧长及扇形的面积 精品同步练习(含解析)
文档属性
| 名称 | 浙教版数学九年级上册3.8弧长及扇形的面积 精品同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-24 13:33:52 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙教版九年级上册数学 3.8弧长及扇形的面积 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径AA′的长为( )
A.π B.2π C.4π D.8π
2.如图,放置在直线l上的扇形OAB,由①图滚动(无滑动)到图②,在由图②滚动到图③,若半径,,则点的路径长为( )
A. B. C. D.
3.如图,点A,B,C在⊙O上,若,,则图中阴影部分的面积为( )
A. B. C. D.
4.如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D、C.若∠ACB=30°,AB=,则阴影部分的面积( )
A. B. C. D.
5.如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上.将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.2cm B.12cm C.6cm D.3cm
6.下列说法中,错误的有( )
①任意三点确定一个圆
②相等的圆心角所对的弧相等
③各边相等的圆内接多边形是正多边形
④若点C是线段AB的黄金分割点,且AB=10,则AC=5-5
A.1个 B.2个 C.3个 D.4个
7.已知,则把它改写成比例式后,错误的是( )
A. B. C. D.
8.有以下命题:
①如果线段是线段,,的第四比例项,则有;
②如果点是线段的中点,那么是、的比例中项;
③如果点是线段的黄金分割点,且,那么是与的比例中项;
④如果点是线段的黄金分割点,,且,则.
其中正确的判断有( )
A.②④ B.①②③④ C.①③④ D.②③④
9.已知线段a,b,c,d是比例线段,其中,,,则d等于( )
A. B. C. D.
10.若,则的值为( )
A.5 B. C.5 D.
填空题(本大题共5小题,每小题4分,共20分。)
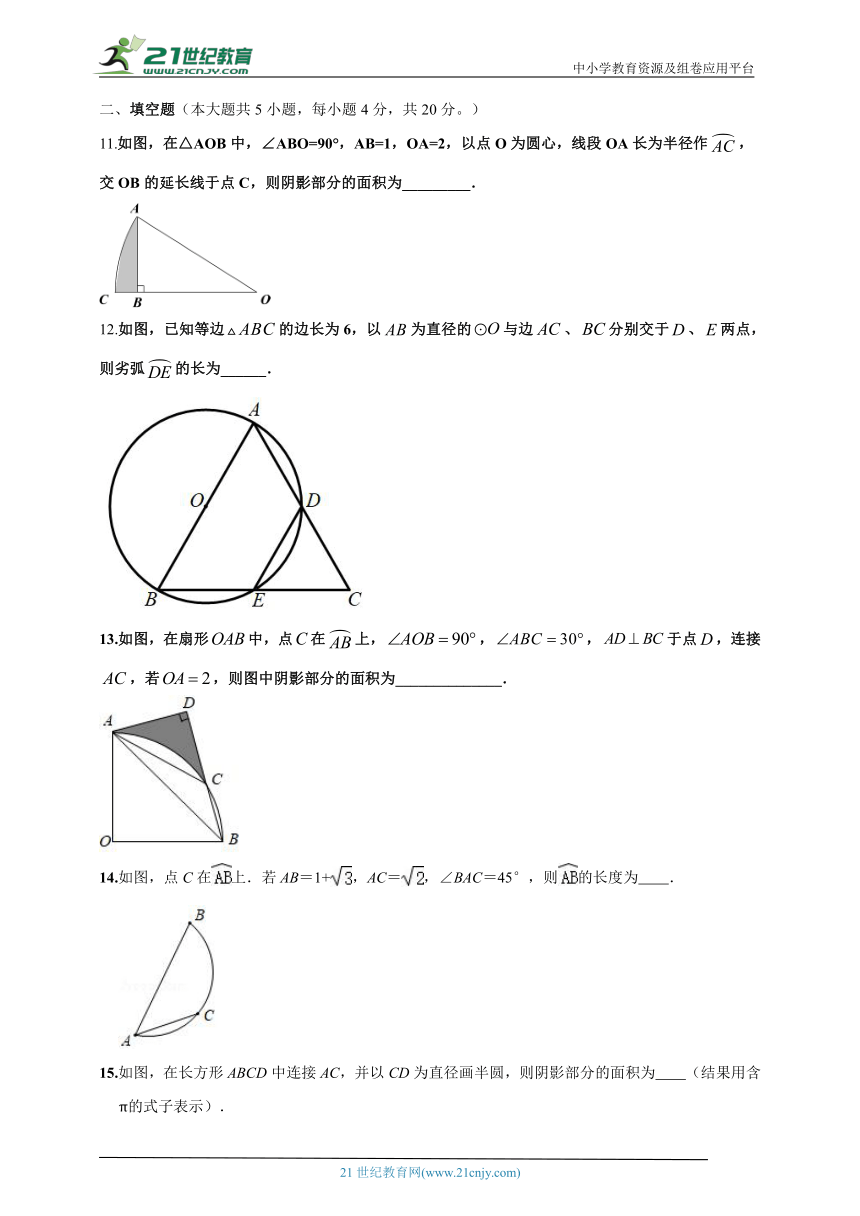
11.如图,在△AOB中,∠ABO=90°,AB=1,OA=2,以点O为圆心,线段OA长为半径作,交OB的延长线于点C,则阴影部分的面积为_________.
12.如图,已知等边的边长为6,以为直径的与边、分别交于、两点,则劣弧的长为______.
13.如图,在扇形中,点在上,,,于点,连接,若,则图中阴影部分的面积为______________.
14.如图,点C在上.若AB=1+,AC=,∠BAC=45°,则的长度为 .
15.如图,在长方形ABCD中连接AC,并以CD为直径画半圆,则阴影部分的面积为 (结果用含π的式子表示).
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
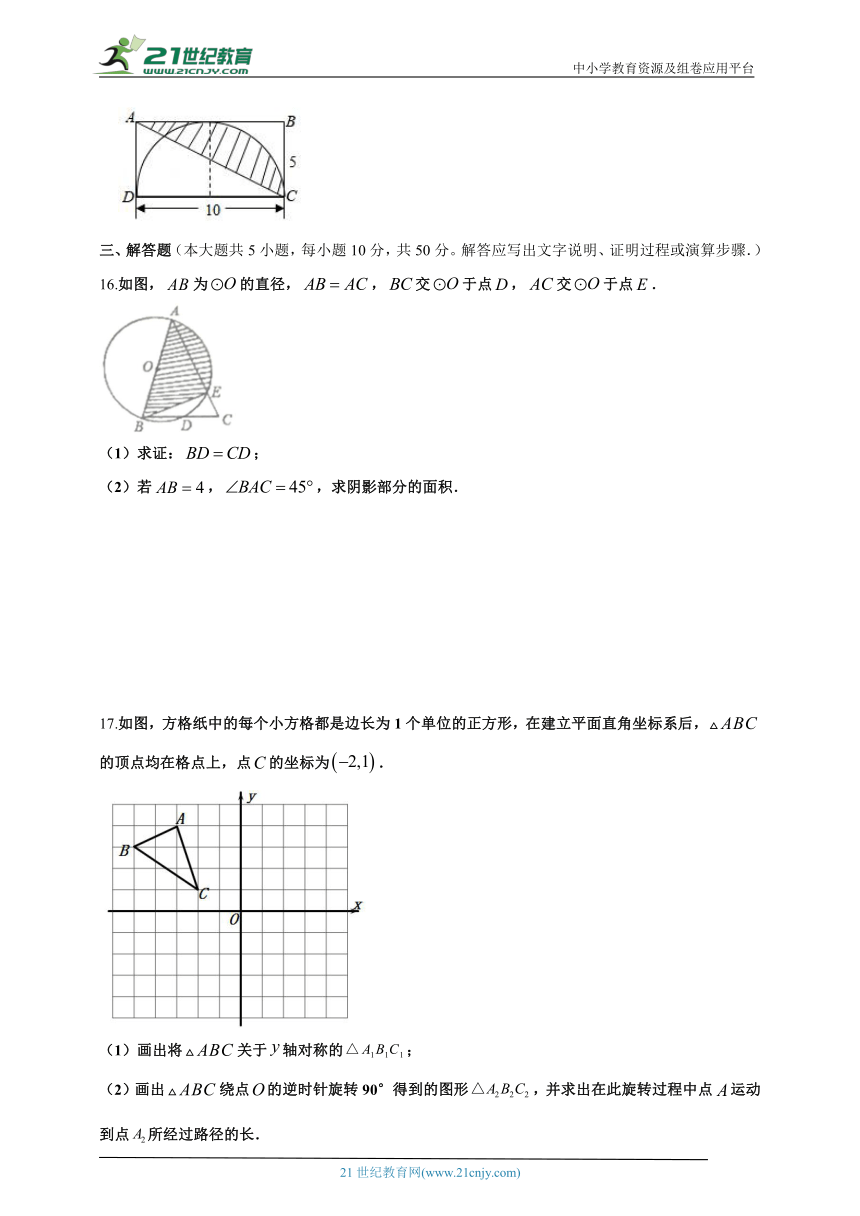
16.如图,为的直径,,交于点,交于点.
(1)求证:;
(2)若,,求阴影部分的面积.
17.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上,点的坐标为.
(1)画出将关于轴对称的;
(2)画出绕点的逆时针旋转90°得到的图形,并求出在此旋转过程中点运动到点所经过路径的长.
18.如图,已知是的直径,C,D是上的点,,交于点E,连结.
(1)求证:;
(2)若,,求图中阴影部分的面积.
19.如图,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2).
(1)画出△OAB关于绕着点O逆时针旋转180°得到的△OA1B1,并写出点B1的坐标;
(2)点A旋转到点A1所经过的路径长为__________(结果保留π).
20.数学活动小组对学校400米的跑道进行规划设计,跑道由两段直道和两端是半圆的弯道组成(如图).其中400米跑道最内圈周长为400米,两端弯道最内圈的半径R=36米.
(1)求跑道中一段直道的长度(π取3.14);
(2)在活动中发现跑道最外圈周长y(米)随跑道总宽度x(米)的变化而变化,请求出y与x的函数关系式;
(3)若跑道最外圈周长为460米,那么最多能铺设道宽为1.2米的跑道多少条?
参考答案
选择题
1.【答案】B
【分析】
由每个小正方形的边长都为1,可求得OA长,然后由弧长公式,求得答案.
【详解】
解:由图可知,OA=4,
∴ O的周长为:8π;
∵∠AO A′=90°,
∴路径AA′为:=2π.
故:选B
2.【答案】B
【分析】
根据题意可画出点的路径图形,利用弧长公式分别表示出三段路线,三段路线相加即可得解.
【详解】
解:∵根据题意可画出图形,如图:
∴通过观察图形可知,
点的路径长为
.
故选:B
3.【答案】C
【分析】
根据圆周角定理求出,再利用扇形面积公式计算即可;
【详解】
..
故答案选C.
4.【答案】C
【分析】
首先求出∠AOB,OB,然后利用S阴=S△ABO S扇形OBD计算即可.
【详解】
连接OB.
∵AB是⊙O切线,
∴OB⊥AB,
∵OC=OB,∠C=30°,
∴∠C=∠OBC=30°,
∴∠AOB=∠C+∠OBC=60°,
在Rt△ABO中,∵∠ABO=90°,AB=,∠A=30°,
∴OB=ABtan30°=1,
∴S阴=S△ABO S扇形OBD=×1× =.
故选:C.
5.【答案】D
【分析】
由圆的直径为,,求出AB的长度,用弧长公式可求得的长度,圆锥的底面圆的周长是的长度列方程求解,即可得到答案.
【详解】
解:
的长度
故选:
6.【答案】A
【分析】
根据确定圆的条件、圆周角定理、圆内接四边形、黄金分割的性质一一判断即可.
【详解】
解:①任意三点确定一个圆;错误,应该的不在同一直线上的三点可以确定一个圆;
②相等的圆心角所对的弧相等;错误,应该是在同圆或等圆中相等的圆心角所对的弧相等;
③各边相等的圆内接多边形是正多边形;正确;
④若点C是线段AB的黄金分割点,且AB=10,则AC=5-5,错误,若点C是线段AB的黄金分割点,且AB=10,则AC=5-5或BC=5-5.;
故选:A.
7.【答案】A
【分析】
根据比例的性质逐项分析即可;
【详解】
A.由交叉相乘得:,与题干不符,故A错误.
B.由交叉相乘得:,与题干一致,故B正确.
C.由交叉相乘得:,与题干一致,故C正确.
D.由交叉相乘得:,与题干一致,故D正确.
故选A.
8.【答案】C
【分析】
根据比例线段、黄金分割的定义逐个判断即可得.
【详解】
①如果线段是线段,,的第四比例项,则有,正确;
②如果点是线段的中点,则,
所以,
所以不是、的比例中项,错误;
③如果点是线段的黄金分割点,且,
则,
所以,即,
所以是与的比例中项,正确;
④如果点是线段的黄金分割点,,且,
则,即,
所以,正确;
综上,正确的判断有①③④,
故选:C.
9.【答案】D
【分析】
根据比例线段的定义得到,然后把,,,代入进行计算即可.
【详解】
解:线段、、、是成比例线段,
,
而,,,
.
故选:D.
10.【答案】C
【分析】
设,则,,,然后代入求值即可.
【详解】
解:设,则,,,
∴===﹣5,
故选:C.
填空题
11.【答案】
【分析】
用扇形面积减去三角形OAB的面积即可.
【详解】
解:∵∠ABO=90°,AB=1,OA=2,
∴OB=,∠O=30°,
∴阴影部分的面积==.
故答案为:.
12.【答案】
【分析】
连接、,由等边三角形的性质得到,再根据含有60角的等腰三角形判定,是等边三角形,最后由等边三角形的性质及弧长公式解题即可.
【详解】
如解图,连接、,∵是等边三角形,∴,∵,,∴,是等边三角形,∴∴,∵,∴的长.
故答案为:
13.【答案】
【分析】
连接OC,过点C作CM⊥OB于点M,分别求出S△ABD、 S△AOB、S△OBC、S扇形AOC,再计算即可求解.
【详解】
解:连接OC,
∵∠AOB=90°
∴△AOB是等腰直角三角形
∵OA=2∴
∵,于点,
∴AD=AB=,BD==
∴S△ABD=
S△AOB=
过点C作CM⊥OB于点M,
∵∠ABC=30°,∴∠AOC=60°
∴∠COB=30°
∴CM=OC=1
∴S△OBC==1
S阴影=S△AOB+S△ABD﹣S△OBC﹣S扇形AOC=2+-1-=
14.
【解答】解:如图,设圆心为O,连接OA,OB,OC,BC,过点C作CT⊥AB于T.
∵∠CTA=90°,∠CAT=45°,AC=,
∴AT=TC=1,
∵AB=1+,
∴BT=,
∴tan∠CBT==,
∴∠CBT=30°,
∴∠AOC=2∠CBT=60°,∠COB=2∠CAB=90°,
∵OA=OC,
∴△AOC是等边三角形,
∴OA=,∠AOB=150°,
∴的长==π,
故答案为:π.
15.【解答】解:设CD的中点为O,半圆与AB相切于点E,AC交OE于J.
∵S△AEJ=S△COJ,
∴S阴=S阴==,
故答案为:.
解答题
16.【答案】(1)见解析;(2)
【分析】
(1)连接AD,由直径得到,然后再由等腰三角形“三线合一”即可得证;
(2)连接OE,阴影部分的面积为扇形AOE和三角形OBE的面积之和.
【详解】
(1)证明:连接,
∵为直径,
∴,
又∵,
∴;
(2)解:连接,
∵,,
∴,,,
∴.
17.【答案】(1)见解析;(2)图见解析,
【分析】
(1)依据轴对称的性质,即可得到△ABC关于y轴对称的△A1B1C1;
(2)依据旋转中心、旋转方向和旋转角度,即可得到△A2B2C2,再根据弧长计算公式,即可得出旋转过程中点A运动到点A2所经过路径的长.
【详解】
解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求;
∵OA=,∠AOA2=90°,
∴在此旋转过程中点A运动到点A2所经过路径的长为:.
18.【答案】(1)见解析;(2)
【分析】
(1)根据圆周角定理得到∠ADB=90°,根据平行线的性质得到∠AEO=∠ADB=90°,即OC⊥AD,于是得到结论;
(2)连接CD,OD,根据等腰三角形的性质得到∠OCB=∠OBC=30°,根据平行线的性质得到∠OCB=∠CBD=30°,求得∠AOD=120°,根据扇形和三角形的面积公式即可得到结论.
【详解】
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,即OC⊥AD,
又∵OC为半径,
∴AE=ED;
(2)解:连接CD,OD,
∵OC=OB,
∴∠OCB=∠OBC=30°,
∴∠AOC=∠OCB+∠OBC=60°,
∵OC∥BD,
∴∠OCB=∠CBD=30°,
∴∠COD=2∠CBD=60°,∠ABD=60°,
∴∠AOD=120°,
∵AB=6,
∴BD=3,AD=3,
∵OA=OB,AE=ED,
∴OE=BD=,
∴S阴影=S扇形AOD-S△AOD==.
19.【答案】(1)作图见解析,B1(-4,-2);(2)4π.
【分析】
(1)将点A和点B分别绕点O逆时针旋转90°后所得对应点,再顺次连接即可得;
(2)根据弧长公式计算可得.
【详解】
解:(1)∴△OA1B1即为所求作三角形,
如图,点B1(-4,-2).
(2)∵OA=4,∠=180°,
∴点A旋转到点A1所经过的路径长为
=4π.
20.【解答】解:(1)设直道的长度为x米,
由题意可得,2π×36+2x=400,
即2×3.14×36+2x=400,
解得x=86.96,
即跑道中一段直道的长度是86.96米;
(2)由题意可得,
y=2π(36+x)+86.96×2=2×3.14×(36+x)+173.92=400+6.28x,
即y与x的函数关系式是y=6.28x+400;
(3)当y=406时,
460=6.28x+400,
解得x≈9.55,
9.55÷1.2≈7.96,
即最多能铺设道宽为1.2米的跑道7条.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版九年级上册数学 3.8弧长及扇形的面积 同步练习
(考试时间:60分钟 满分:100分)
选择题(本大题共10小题,每小题3分,共30分。下列各题的备选答案中,只有一项是最符合题意的,请选出。)
1.如图,在5×5的正方形网格中,每个小正方形的边长都为1,若将△AOB绕点O顺时针旋转90°得到△A′OB′,则A点运动的路径AA′的长为( )
A.π B.2π C.4π D.8π
2.如图,放置在直线l上的扇形OAB,由①图滚动(无滑动)到图②,在由图②滚动到图③,若半径,,则点的路径长为( )
A. B. C. D.
3.如图,点A,B,C在⊙O上,若,,则图中阴影部分的面积为( )
A. B. C. D.
4.如图,AB是⊙O的切线,B为切点,AC经过点O,与⊙O分别相交于点D、C.若∠ACB=30°,AB=,则阴影部分的面积( )
A. B. C. D.
5.如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上.将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是( )
A.2cm B.12cm C.6cm D.3cm
6.下列说法中,错误的有( )
①任意三点确定一个圆
②相等的圆心角所对的弧相等
③各边相等的圆内接多边形是正多边形
④若点C是线段AB的黄金分割点,且AB=10,则AC=5-5
A.1个 B.2个 C.3个 D.4个
7.已知,则把它改写成比例式后,错误的是( )
A. B. C. D.
8.有以下命题:
①如果线段是线段,,的第四比例项,则有;
②如果点是线段的中点,那么是、的比例中项;
③如果点是线段的黄金分割点,且,那么是与的比例中项;
④如果点是线段的黄金分割点,,且,则.
其中正确的判断有( )
A.②④ B.①②③④ C.①③④ D.②③④
9.已知线段a,b,c,d是比例线段,其中,,,则d等于( )
A. B. C. D.
10.若,则的值为( )
A.5 B. C.5 D.
填空题(本大题共5小题,每小题4分,共20分。)
11.如图,在△AOB中,∠ABO=90°,AB=1,OA=2,以点O为圆心,线段OA长为半径作,交OB的延长线于点C,则阴影部分的面积为_________.
12.如图,已知等边的边长为6,以为直径的与边、分别交于、两点,则劣弧的长为______.
13.如图,在扇形中,点在上,,,于点,连接,若,则图中阴影部分的面积为______________.
14.如图,点C在上.若AB=1+,AC=,∠BAC=45°,则的长度为 .
15.如图,在长方形ABCD中连接AC,并以CD为直径画半圆,则阴影部分的面积为 (结果用含π的式子表示).
三、解答题(本大题共5小题,每小题10分,共50分。解答应写出文字说明、证明过程或演算步骤.)
16.如图,为的直径,,交于点,交于点.
(1)求证:;
(2)若,,求阴影部分的面积.
17.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上,点的坐标为.
(1)画出将关于轴对称的;
(2)画出绕点的逆时针旋转90°得到的图形,并求出在此旋转过程中点运动到点所经过路径的长.
18.如图,已知是的直径,C,D是上的点,,交于点E,连结.
(1)求证:;
(2)若,,求图中阴影部分的面积.
19.如图,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2).
(1)画出△OAB关于绕着点O逆时针旋转180°得到的△OA1B1,并写出点B1的坐标;
(2)点A旋转到点A1所经过的路径长为__________(结果保留π).
20.数学活动小组对学校400米的跑道进行规划设计,跑道由两段直道和两端是半圆的弯道组成(如图).其中400米跑道最内圈周长为400米,两端弯道最内圈的半径R=36米.
(1)求跑道中一段直道的长度(π取3.14);
(2)在活动中发现跑道最外圈周长y(米)随跑道总宽度x(米)的变化而变化,请求出y与x的函数关系式;
(3)若跑道最外圈周长为460米,那么最多能铺设道宽为1.2米的跑道多少条?
参考答案
选择题
1.【答案】B
【分析】
由每个小正方形的边长都为1,可求得OA长,然后由弧长公式,求得答案.
【详解】
解:由图可知,OA=4,
∴ O的周长为:8π;
∵∠AO A′=90°,
∴路径AA′为:=2π.
故:选B
2.【答案】B
【分析】
根据题意可画出点的路径图形,利用弧长公式分别表示出三段路线,三段路线相加即可得解.
【详解】
解:∵根据题意可画出图形,如图:
∴通过观察图形可知,
点的路径长为
.
故选:B
3.【答案】C
【分析】
根据圆周角定理求出,再利用扇形面积公式计算即可;
【详解】
..
故答案选C.
4.【答案】C
【分析】
首先求出∠AOB,OB,然后利用S阴=S△ABO S扇形OBD计算即可.
【详解】
连接OB.
∵AB是⊙O切线,
∴OB⊥AB,
∵OC=OB,∠C=30°,
∴∠C=∠OBC=30°,
∴∠AOB=∠C+∠OBC=60°,
在Rt△ABO中,∵∠ABO=90°,AB=,∠A=30°,
∴OB=ABtan30°=1,
∴S阴=S△ABO S扇形OBD=×1× =.
故选:C.
5.【答案】D
【分析】
由圆的直径为,,求出AB的长度,用弧长公式可求得的长度,圆锥的底面圆的周长是的长度列方程求解,即可得到答案.
【详解】
解:
的长度
故选:
6.【答案】A
【分析】
根据确定圆的条件、圆周角定理、圆内接四边形、黄金分割的性质一一判断即可.
【详解】
解:①任意三点确定一个圆;错误,应该的不在同一直线上的三点可以确定一个圆;
②相等的圆心角所对的弧相等;错误,应该是在同圆或等圆中相等的圆心角所对的弧相等;
③各边相等的圆内接多边形是正多边形;正确;
④若点C是线段AB的黄金分割点,且AB=10,则AC=5-5,错误,若点C是线段AB的黄金分割点,且AB=10,则AC=5-5或BC=5-5.;
故选:A.
7.【答案】A
【分析】
根据比例的性质逐项分析即可;
【详解】
A.由交叉相乘得:,与题干不符,故A错误.
B.由交叉相乘得:,与题干一致,故B正确.
C.由交叉相乘得:,与题干一致,故C正确.
D.由交叉相乘得:,与题干一致,故D正确.
故选A.
8.【答案】C
【分析】
根据比例线段、黄金分割的定义逐个判断即可得.
【详解】
①如果线段是线段,,的第四比例项,则有,正确;
②如果点是线段的中点,则,
所以,
所以不是、的比例中项,错误;
③如果点是线段的黄金分割点,且,
则,
所以,即,
所以是与的比例中项,正确;
④如果点是线段的黄金分割点,,且,
则,即,
所以,正确;
综上,正确的判断有①③④,
故选:C.
9.【答案】D
【分析】
根据比例线段的定义得到,然后把,,,代入进行计算即可.
【详解】
解:线段、、、是成比例线段,
,
而,,,
.
故选:D.
10.【答案】C
【分析】
设,则,,,然后代入求值即可.
【详解】
解:设,则,,,
∴===﹣5,
故选:C.
填空题
11.【答案】
【分析】
用扇形面积减去三角形OAB的面积即可.
【详解】
解:∵∠ABO=90°,AB=1,OA=2,
∴OB=,∠O=30°,
∴阴影部分的面积==.
故答案为:.
12.【答案】
【分析】
连接、,由等边三角形的性质得到,再根据含有60角的等腰三角形判定,是等边三角形,最后由等边三角形的性质及弧长公式解题即可.
【详解】
如解图,连接、,∵是等边三角形,∴,∵,,∴,是等边三角形,∴∴,∵,∴的长.
故答案为:
13.【答案】
【分析】
连接OC,过点C作CM⊥OB于点M,分别求出S△ABD、 S△AOB、S△OBC、S扇形AOC,再计算即可求解.
【详解】
解:连接OC,
∵∠AOB=90°
∴△AOB是等腰直角三角形
∵OA=2∴
∵,于点,
∴AD=AB=,BD==
∴S△ABD=
S△AOB=
过点C作CM⊥OB于点M,
∵∠ABC=30°,∴∠AOC=60°
∴∠COB=30°
∴CM=OC=1
∴S△OBC==1
S阴影=S△AOB+S△ABD﹣S△OBC﹣S扇形AOC=2+-1-=
14.
【解答】解:如图,设圆心为O,连接OA,OB,OC,BC,过点C作CT⊥AB于T.
∵∠CTA=90°,∠CAT=45°,AC=,
∴AT=TC=1,
∵AB=1+,
∴BT=,
∴tan∠CBT==,
∴∠CBT=30°,
∴∠AOC=2∠CBT=60°,∠COB=2∠CAB=90°,
∵OA=OC,
∴△AOC是等边三角形,
∴OA=,∠AOB=150°,
∴的长==π,
故答案为:π.
15.【解答】解:设CD的中点为O,半圆与AB相切于点E,AC交OE于J.
∵S△AEJ=S△COJ,
∴S阴=S阴==,
故答案为:.
解答题
16.【答案】(1)见解析;(2)
【分析】
(1)连接AD,由直径得到,然后再由等腰三角形“三线合一”即可得证;
(2)连接OE,阴影部分的面积为扇形AOE和三角形OBE的面积之和.
【详解】
(1)证明:连接,
∵为直径,
∴,
又∵,
∴;
(2)解:连接,
∵,,
∴,,,
∴.
17.【答案】(1)见解析;(2)图见解析,
【分析】
(1)依据轴对称的性质,即可得到△ABC关于y轴对称的△A1B1C1;
(2)依据旋转中心、旋转方向和旋转角度,即可得到△A2B2C2,再根据弧长计算公式,即可得出旋转过程中点A运动到点A2所经过路径的长.
【详解】
解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C2即为所求;
∵OA=,∠AOA2=90°,
∴在此旋转过程中点A运动到点A2所经过路径的长为:.
18.【答案】(1)见解析;(2)
【分析】
(1)根据圆周角定理得到∠ADB=90°,根据平行线的性质得到∠AEO=∠ADB=90°,即OC⊥AD,于是得到结论;
(2)连接CD,OD,根据等腰三角形的性质得到∠OCB=∠OBC=30°,根据平行线的性质得到∠OCB=∠CBD=30°,求得∠AOD=120°,根据扇形和三角形的面积公式即可得到结论.
【详解】
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AEO=∠ADB=90°,即OC⊥AD,
又∵OC为半径,
∴AE=ED;
(2)解:连接CD,OD,
∵OC=OB,
∴∠OCB=∠OBC=30°,
∴∠AOC=∠OCB+∠OBC=60°,
∵OC∥BD,
∴∠OCB=∠CBD=30°,
∴∠COD=2∠CBD=60°,∠ABD=60°,
∴∠AOD=120°,
∵AB=6,
∴BD=3,AD=3,
∵OA=OB,AE=ED,
∴OE=BD=,
∴S阴影=S扇形AOD-S△AOD==.
19.【答案】(1)作图见解析,B1(-4,-2);(2)4π.
【分析】
(1)将点A和点B分别绕点O逆时针旋转90°后所得对应点,再顺次连接即可得;
(2)根据弧长公式计算可得.
【详解】
解:(1)∴△OA1B1即为所求作三角形,
如图,点B1(-4,-2).
(2)∵OA=4,∠=180°,
∴点A旋转到点A1所经过的路径长为
=4π.
20.【解答】解:(1)设直道的长度为x米,
由题意可得,2π×36+2x=400,
即2×3.14×36+2x=400,
解得x=86.96,
即跑道中一段直道的长度是86.96米;
(2)由题意可得,
y=2π(36+x)+86.96×2=2×3.14×(36+x)+173.92=400+6.28x,
即y与x的函数关系式是y=6.28x+400;
(3)当y=406时,
460=6.28x+400,
解得x≈9.55,
9.55÷1.2≈7.96,
即最多能铺设道宽为1.2米的跑道7条.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
