浙教版数学七年级上册第一章-第三章 综合练习(含答案)
文档属性
| 名称 | 浙教版数学七年级上册第一章-第三章 综合练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 131.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-25 15:23:09 | ||
图片预览


文档简介
浙教版数学七年级上册第一章-第三章
一、单选题
1.北京冬奥村是2022年北京冬季奥运会、冬残奥会最大的非竞赛类场馆之一,总建筑面积约38.66万平方米,其中38.66万用科学记数法可表示为( )
A. B. C. D.
2.-6的相反数是( )
A. B.-6 C. D.6
3.下列各数中,是无理数的是( )
A.2 B. C.3.14159 D.
4.4的平方根是x,27的立方根是y,则的值为( )
A.2 B.3 C.5或1 D.5或-1
5.对4袋标注质量为 的食品的实际质量进行检测,检测结果(用正数记超过标准质量的克数,用负数记不足标准质量的克数)如下表:
袋数 第1袋 第2袋 第3袋 第4袋
检测结果/ -2 +3 -5 +4
最接近标准质量的是( )
A.第1袋 B.第2袋 C.第3袋 D.第4袋
6.如图,在做浮力实验时,小华用一根细线将一个正方体铁块拴住,完全浸入盛满水的圆柱形烧杯中,并用一个量筒量得溢出水的体积为,由此可估计该正方体铁块的棱长位于哪两个相邻的整数之间( )
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
7.下列每对数中,不相等的一对是( )
A.(﹣2)4和﹣24 B.(﹣2)3 和﹣23
C.(﹣2)2和 22 D.|﹣2|3和 23
8.已知 为实数,下列说法:①若 互为相反数,则 ;②若 ,则 ;③若 , ,则 ;④若 ,则 ;⑤若 且 ,则 ,其中正确的是( ).
A.①② B.②③ C.③④ D.④⑤
9.若a、b、c、d四个数满足 ,则a、b、c、d四个数的大小关系为( )
A.a>c>b>d B.b>d>a>c C.d>b>a>c D.c>a>b>d
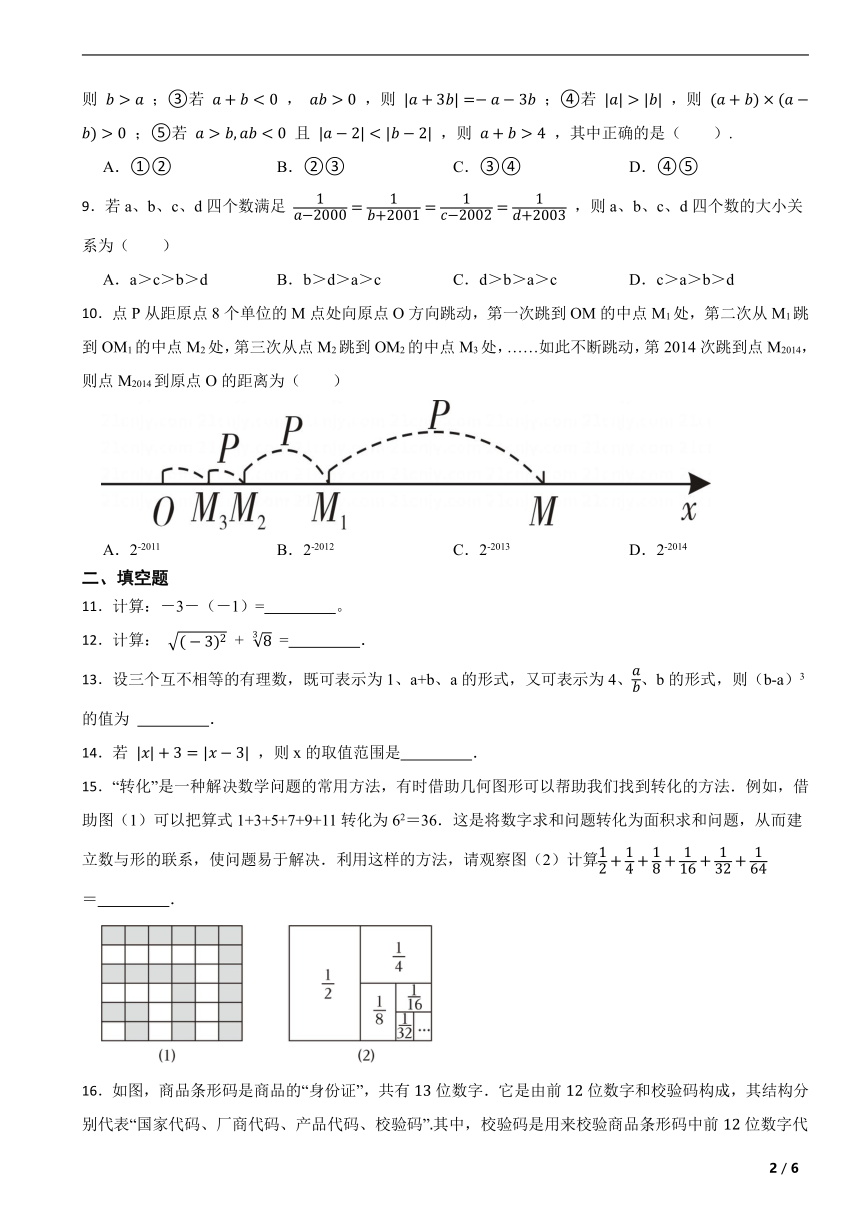
10.点P从距原点8个单位的M点处向原点O方向跳动,第一次跳到OM的中点M1处,第二次从M1跳到OM1的中点M2处,第三次从点M2跳到OM2的中点M3处,……如此不断跳动,第2014次跳到点M2014,则点M2014到原点O的距离为( )
A.2-2011 B.2-2012 C.2-2013 D.2-2014
二、填空题
11.计算:-3-(-1)= 。
12.计算: + = .
13.设三个互不相等的有理数,既可表示为1、a+b、a的形式,又可表示为4、、b的形式,则(b-a)3的值为 .
14.若 ,则x的取值范围是 .
15.“转化”是一种解决数学问题的常用方法,有时借助几何图形可以帮助我们找到转化的方法.例如,借助图(1)可以把算式1+3+5+7+9+11转化为62=36.这是将数字求和问题转化为面积求和问题,从而建立数与形的联系,使问题易于解决.利用这样的方法,请观察图(2)计算= .
16.如图,商品条形码是商品的“身份证”,共有位数字.它是由前位数字和校验码构成,其结构分别代表“国家代码、厂商代码、产品代码、校验码”其中,校验码是用来校验商品条形码中前位数字代码的正确性.它的编制是按照特定的算法得来的.其算法为:
步骤:计算前位数字中偶数位数字的和,即;
步骤:计算前位数字中奇数位数字的和,即;
步骤:计算与的和,即;
步骤:取大于或等于且为的整数倍的最小数,即;
步骤:计算与的差就是校验码,即.
如图,若条形码中被污染的两个数字的和是,则被污染的两个数字中右边的数字是 .
三、解答题
17.把下列各数在数轴上表示出来,并用“<”把它们连接起来.3.5,0,-4,2,.
18.若a>0,b<0,且|x-a|+|x-b|=a-b,求x的取值范围.
19.已知的平方根是,的立方根是2.
(1)求和的值;
(2)若,是整数,求的算术平方根.
20.今年以来,由于受国际天然气形势的影响,我国天然气市场总体呈现量紧价高的态势,为确保天然气保供稳价,提高居民生活用气的保障,某地决定从今年11月开始调整居民用气价格,调整前后价格如表(每月用气量为a立方米):
用气类别
第一档(0<a≤60) 第二档(60<a≤80) 第三档(a>80)
调整前 2.60 2.90 3.65
调整后 2.95 3.25 4.10
注:该地天然气收费按月实行阶梯收费
(1)某用户10月(调整前)缴天然气费91元,求该用户这月用气量;
(2)若该用户11月(调整后)用气量与10月相同,则该用户11月比10月多缴费多少元?
(3)因天气转冷,该用户今年12月因取暖用气量急剧增加,缴天然气费283元,该用户今年12月用气量是多少立方米?
21.阅读材料,解答问题:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,将这个数减去其整数部分,差就是小数部分,因为的整数部分是1,于是用来表示的小数部分.又例如:∵,即
∴的整数部分是2,小数部分为.
(1)的整数部分是 ,小数部分是 ;
(2)若,其中是整数,且,求的值.
22.先观察下列等式,再解答下列问题:
①;
②;
③.
(1)请你根据上面三个等式提供的信息,直接写出第五个等式:________;
(2)请你按照上面各等式反映的规律,试写出第n个等式(用含n的式子表示,n为正整数);
(3)设(n为正整数),当时,求S的值.
23.在数轴上,我们可以利用线段端点表示的两个数进行减法运算的方法,即大的数减去小的数,求线段的长度.如图,在数轴上,点A、B、C示的数分别是-2、0、3.线段AB= 0 - (-2) =2;线段BC = 3 - 0 = 3;线段AC = 3 - (-2) = 5.
(1)若点E、F表示的数分别是-8 和2,则线段EF的长为 .
(2)点M、N为数轴上的两个动点.点N在点M的左边,点M表示的数是-5,若线段MN的长为 12,则点 N表示的数是 .
(3)点 P、Q为数轴上的两个动点.动点 P从点A 出发,以每秒2个单位长度的速度沿A一C一A 运动.动点Q从点 C出发,以每秒1个单位长度的速度沿数轴向终点A运动.设点P、Q的运动时间为t(t>0)秒.
①当点P沿A一C运动时,求点P、Q相遇时t的值
②当点B将线段PQ分成的两部分的比为1:4时,直接写出t的值.
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】D
4.【答案】C
5.【答案】A
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】D
10.【答案】A
11.【答案】-2
12.【答案】5
13.【答案】0或-8
14.【答案】
15.【答案】
16.【答案】4
17.【答案】解:各数在数轴上表示如下
用 “<” 连接
18.【答案】解:∵a>0,b<0,
∴a-b>0,
又∵|x-a|+|x-b|=a-b,
即a-x+x-b=a-b
∴x-a<0且x-b>0,
∴b<x<a;
当x=a时, a-x+x-b = a-a+a-b =a-b,成立;
当x=b时, a-x+x-b = a-b+b-b =a-b,成立;
∴ b≤x≤a
19.【答案】(1),
(2)3
20.【答案】(1)解:调整前第一档的最高收费为2.6×60=156(元),
∴该用户是第一档用气量,
91÷2.6=35 (m3),
该用户10月的用气量为35m3;
(2)解:由题知:该用户11月的用气量为35m3需要缴费的金额为:35×2.95=103.25,
103.25﹣91=12.25(元),
故该用户11月比10月多缴费12.25元;
(3)解:调整后第1档的最高收费为:2.95×60=177(元),
调整后第2档的最高收费为:3.25×20=65(元),
177+65=242(元),
故该用户12月的用气量超过了80m3,(283﹣242)÷4.1=10(m3),
∴12月用气量为80+10=90(m3).
21.【答案】(1)5,
(2)
22.【答案】(1)
(2)
(3)
23.【答案】(1)10
(2)-17
(3)解: ①; ② t的值为或或
1 / 1
一、单选题
1.北京冬奥村是2022年北京冬季奥运会、冬残奥会最大的非竞赛类场馆之一,总建筑面积约38.66万平方米,其中38.66万用科学记数法可表示为( )
A. B. C. D.
2.-6的相反数是( )
A. B.-6 C. D.6
3.下列各数中,是无理数的是( )
A.2 B. C.3.14159 D.
4.4的平方根是x,27的立方根是y,则的值为( )
A.2 B.3 C.5或1 D.5或-1
5.对4袋标注质量为 的食品的实际质量进行检测,检测结果(用正数记超过标准质量的克数,用负数记不足标准质量的克数)如下表:
袋数 第1袋 第2袋 第3袋 第4袋
检测结果/ -2 +3 -5 +4
最接近标准质量的是( )
A.第1袋 B.第2袋 C.第3袋 D.第4袋
6.如图,在做浮力实验时,小华用一根细线将一个正方体铁块拴住,完全浸入盛满水的圆柱形烧杯中,并用一个量筒量得溢出水的体积为,由此可估计该正方体铁块的棱长位于哪两个相邻的整数之间( )
A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间
7.下列每对数中,不相等的一对是( )
A.(﹣2)4和﹣24 B.(﹣2)3 和﹣23
C.(﹣2)2和 22 D.|﹣2|3和 23
8.已知 为实数,下列说法:①若 互为相反数,则 ;②若 ,则 ;③若 , ,则 ;④若 ,则 ;⑤若 且 ,则 ,其中正确的是( ).
A.①② B.②③ C.③④ D.④⑤
9.若a、b、c、d四个数满足 ,则a、b、c、d四个数的大小关系为( )
A.a>c>b>d B.b>d>a>c C.d>b>a>c D.c>a>b>d
10.点P从距原点8个单位的M点处向原点O方向跳动,第一次跳到OM的中点M1处,第二次从M1跳到OM1的中点M2处,第三次从点M2跳到OM2的中点M3处,……如此不断跳动,第2014次跳到点M2014,则点M2014到原点O的距离为( )
A.2-2011 B.2-2012 C.2-2013 D.2-2014
二、填空题
11.计算:-3-(-1)= 。
12.计算: + = .
13.设三个互不相等的有理数,既可表示为1、a+b、a的形式,又可表示为4、、b的形式,则(b-a)3的值为 .
14.若 ,则x的取值范围是 .
15.“转化”是一种解决数学问题的常用方法,有时借助几何图形可以帮助我们找到转化的方法.例如,借助图(1)可以把算式1+3+5+7+9+11转化为62=36.这是将数字求和问题转化为面积求和问题,从而建立数与形的联系,使问题易于解决.利用这样的方法,请观察图(2)计算= .
16.如图,商品条形码是商品的“身份证”,共有位数字.它是由前位数字和校验码构成,其结构分别代表“国家代码、厂商代码、产品代码、校验码”其中,校验码是用来校验商品条形码中前位数字代码的正确性.它的编制是按照特定的算法得来的.其算法为:
步骤:计算前位数字中偶数位数字的和,即;
步骤:计算前位数字中奇数位数字的和,即;
步骤:计算与的和,即;
步骤:取大于或等于且为的整数倍的最小数,即;
步骤:计算与的差就是校验码,即.
如图,若条形码中被污染的两个数字的和是,则被污染的两个数字中右边的数字是 .
三、解答题
17.把下列各数在数轴上表示出来,并用“<”把它们连接起来.3.5,0,-4,2,.
18.若a>0,b<0,且|x-a|+|x-b|=a-b,求x的取值范围.
19.已知的平方根是,的立方根是2.
(1)求和的值;
(2)若,是整数,求的算术平方根.
20.今年以来,由于受国际天然气形势的影响,我国天然气市场总体呈现量紧价高的态势,为确保天然气保供稳价,提高居民生活用气的保障,某地决定从今年11月开始调整居民用气价格,调整前后价格如表(每月用气量为a立方米):
用气类别
第一档(0<a≤60) 第二档(60<a≤80) 第三档(a>80)
调整前 2.60 2.90 3.65
调整后 2.95 3.25 4.10
注:该地天然气收费按月实行阶梯收费
(1)某用户10月(调整前)缴天然气费91元,求该用户这月用气量;
(2)若该用户11月(调整后)用气量与10月相同,则该用户11月比10月多缴费多少元?
(3)因天气转冷,该用户今年12月因取暖用气量急剧增加,缴天然气费283元,该用户今年12月用气量是多少立方米?
21.阅读材料,解答问题:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,将这个数减去其整数部分,差就是小数部分,因为的整数部分是1,于是用来表示的小数部分.又例如:∵,即
∴的整数部分是2,小数部分为.
(1)的整数部分是 ,小数部分是 ;
(2)若,其中是整数,且,求的值.
22.先观察下列等式,再解答下列问题:
①;
②;
③.
(1)请你根据上面三个等式提供的信息,直接写出第五个等式:________;
(2)请你按照上面各等式反映的规律,试写出第n个等式(用含n的式子表示,n为正整数);
(3)设(n为正整数),当时,求S的值.
23.在数轴上,我们可以利用线段端点表示的两个数进行减法运算的方法,即大的数减去小的数,求线段的长度.如图,在数轴上,点A、B、C示的数分别是-2、0、3.线段AB= 0 - (-2) =2;线段BC = 3 - 0 = 3;线段AC = 3 - (-2) = 5.
(1)若点E、F表示的数分别是-8 和2,则线段EF的长为 .
(2)点M、N为数轴上的两个动点.点N在点M的左边,点M表示的数是-5,若线段MN的长为 12,则点 N表示的数是 .
(3)点 P、Q为数轴上的两个动点.动点 P从点A 出发,以每秒2个单位长度的速度沿A一C一A 运动.动点Q从点 C出发,以每秒1个单位长度的速度沿数轴向终点A运动.设点P、Q的运动时间为t(t>0)秒.
①当点P沿A一C运动时,求点P、Q相遇时t的值
②当点B将线段PQ分成的两部分的比为1:4时,直接写出t的值.
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】D
4.【答案】C
5.【答案】A
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】D
10.【答案】A
11.【答案】-2
12.【答案】5
13.【答案】0或-8
14.【答案】
15.【答案】
16.【答案】4
17.【答案】解:各数在数轴上表示如下
用 “<” 连接
18.【答案】解:∵a>0,b<0,
∴a-b>0,
又∵|x-a|+|x-b|=a-b,
即a-x+x-b=a-b
∴x-a<0且x-b>0,
∴b<x<a;
当x=a时, a-x+x-b = a-a+a-b =a-b,成立;
当x=b时, a-x+x-b = a-b+b-b =a-b,成立;
∴ b≤x≤a
19.【答案】(1),
(2)3
20.【答案】(1)解:调整前第一档的最高收费为2.6×60=156(元),
∴该用户是第一档用气量,
91÷2.6=35 (m3),
该用户10月的用气量为35m3;
(2)解:由题知:该用户11月的用气量为35m3需要缴费的金额为:35×2.95=103.25,
103.25﹣91=12.25(元),
故该用户11月比10月多缴费12.25元;
(3)解:调整后第1档的最高收费为:2.95×60=177(元),
调整后第2档的最高收费为:3.25×20=65(元),
177+65=242(元),
故该用户12月的用气量超过了80m3,(283﹣242)÷4.1=10(m3),
∴12月用气量为80+10=90(m3).
21.【答案】(1)5,
(2)
22.【答案】(1)
(2)
(3)
23.【答案】(1)10
(2)-17
(3)解: ①; ② t的值为或或
1 / 1
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
