2.2二次函数的图象（一）

课件14张PPT。2.2 二次函数的图象(1)回顾知识:一、正比例函数y=kx（k ≠ 0）其图象是什么？二、一次函数y=kx+b（k ≠ 0）其图象又是什么？是一条经过原点的直线.是一条直线.是双曲线.三、反比例函数 （k ≠ 0）其图象又是什么？ 二次函数y=ax2+ bx+c（a ≠ 0）
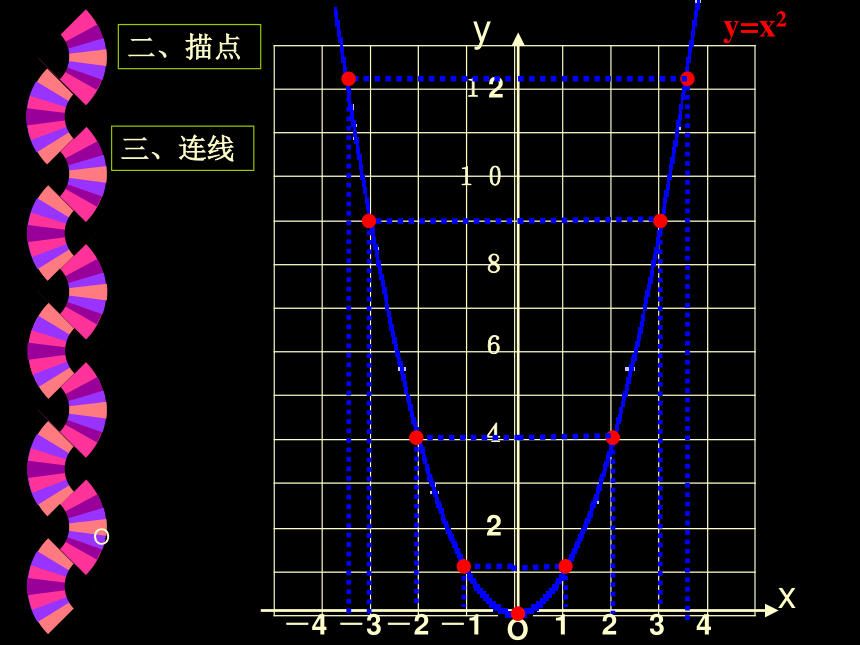
其图象又是什么呢？.二次函数y=ax2的图像一、列表 4 9 12.25 1 49 12.25用 描点法画二次函数 的图象O－4二、描点三、连线x y y=x2－4在同一坐标系中画二次函数 与 的图像。二次函数 的图像是一条关于y轴对称，过坐标原点并向上伸展的曲线，像这样的曲线通常叫做抛物线，抛物线与它的对称轴的交点叫做抛物线的顶点。观察发现1、二次函数 的图像与
的图像关于什么对称？2、如果已知 的图像，怎样更方便地得到 的图像？－2－1－321O312345－1－2－3－4－5Oyxy=2x2............0-1.5-1-0.511.50.500.524.50.524.5y=-2x2...-4.5-2-0.50-0.5-2-4.5...xy=2x2y=-2x2（0，0）（0，0）y轴y轴在x轴的上方（除顶点外）在x轴的下方（除顶点外）向上向下当x=0时，最小值为0。当x=0时，最大值为0。观察左图，并完成填空。y=2x2y=-2x21、抛物线y=ax2的顶点是原点，对称轴是y轴。2、当a>0时，抛物线的开口向上，顶点是抛物线上的最低点，在对称轴的左侧，y随着x的增大而减小；在对称轴右侧，y随着x的增大而增大。当x=0时函数y的值最小；
当a<0时，抛物线的开口向下，顶点是抛物线上的最高点，在对称轴的左侧，y随着x的增大而增大；在对称轴右侧，y随着x的增大而减小。当x=0时函数y的值最大；
二次函数y=ax2的性质 例1、已知二次函数y=ax2(a≠0)的图像经过点(-2,-3).(1)求a的值，并写出这个二次函数的解析式.
(2)说出这个二次函数的顶点坐标、对称轴、开口方向和图像的位置.练习一、若抛物线y=ax2 （a ≠ 0），过点（－1，3）.

（1）则a的值是 ；

（2）对称轴是 ，开口 .
（3）顶点坐标是 ，顶点是抛物线上的 .
抛物线在x轴的 方（除顶点外）.3y轴向上（0，0）最低点上谈收获:1.二次函数y=ax2(a≠0)的图像是一条抛物线.2.图象关于y轴对称,顶点是坐标原点.3.当a>0时,抛物线的开口向上,顶点是抛物线上的最低点;当a<0时,抛物线的开口向下,顶点是抛物线的最高点.1.课本P 31---32 页作业题
2.作业本再见作业：