专题01 运算思维之整式的加减综合应用专练(解析版)-【考点培优尖子生专用】七年级数学(浙教版)
文档属性
| 名称 | 专题01 运算思维之整式的加减综合应用专练(解析版)-【考点培优尖子生专用】七年级数学(浙教版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-31 10:18:59 | ||
图片预览



文档简介
专题01 运算思维之整式的加减综合 专项练习
一、单选题
1.如图,从边长为(a+4)的正方形纸片中剪去一个边长为(a+1)的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形ABCD(不重叠无缝隙),则AD,AB的长分别是( )
A.3,2a+5 B.5,2a+8 C.5,2a+3 D.3,2a+2
2.如果和互为相反数,那么多项式的值是( )
A.-3 B.-1 C.1 D.3
3.某水果商店在甲批发市场以每千克元的价格购进30千克的橘子,又在乙批发市场以每千克元()的价格购进同样的50千克橘子.如果以每千克元的价格全部卖出这种橘子,那么这家商店( )
A.盈利了 B.亏损了 C.不盈不亏 D.盈亏不能确定
4.如图,两个长方形的面积分别为20,6,两阴影部分的面积分别为a,b,且,则等于( )
A.6 B.7 C.14 D.16
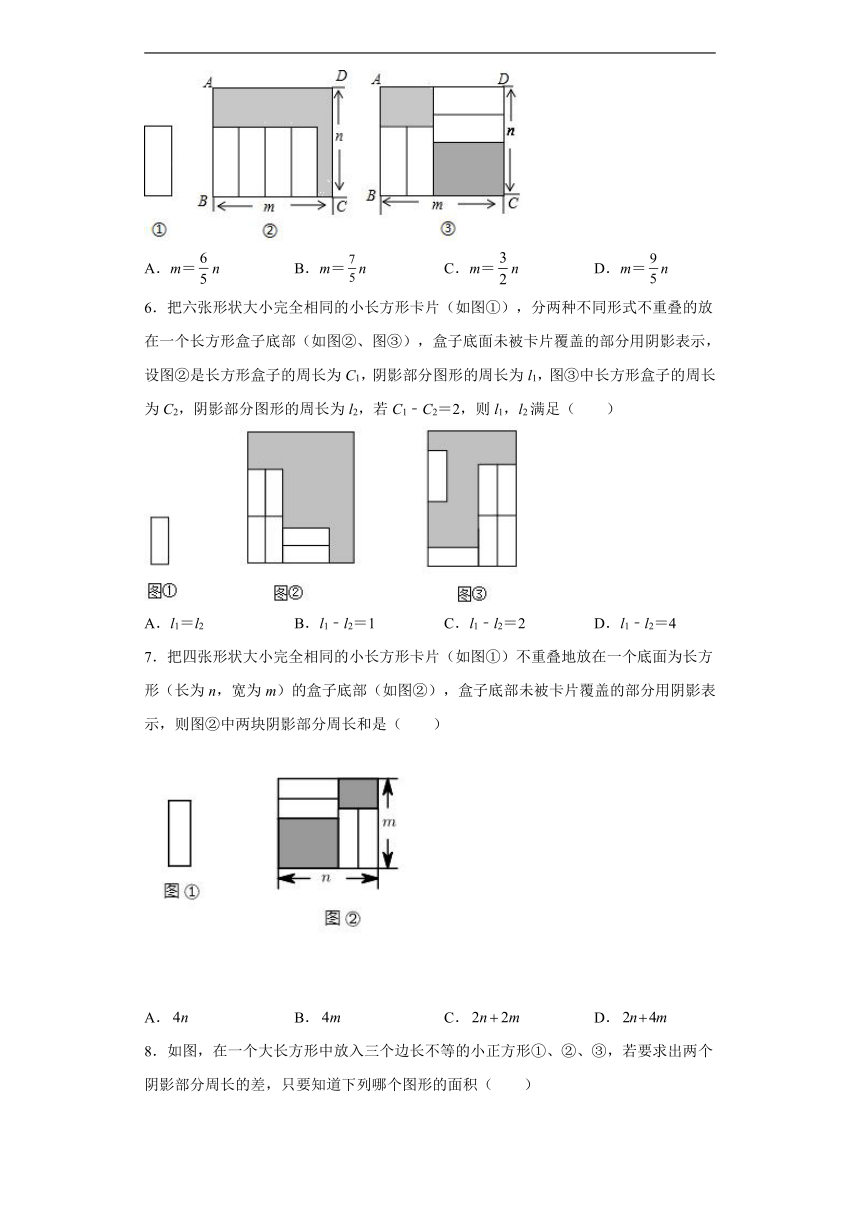
5.把四张形状大小完全相同的小长方形卡片(如图①),分两种不同形式不重叠的放在一个底面长为m,宽为n的长方形盒子底部(如图②、图③),盒子底面未被卡片覆盖的部分用阴影表示,设图②中阴影部分图形的周长为l1,图③中两个阴影部分图形的周长和为l2,若,则m,n满足( )
A.m=n B.m=n C.m=n D.m=n
6.把六张形状大小完全相同的小长方形卡片(如图①),分两种不同形式不重叠的放在一个长方形盒子底部(如图②、图③),盒子底面未被卡片覆盖的部分用阴影表示,设图②是长方形盒子的周长为C1,阴影部分图形的周长为l1,图③中长方形盒子的周长为C2,阴影部分图形的周长为l2,若C1﹣C2=2,则l1,l2满足( )
A.l1=l2 B.l1﹣l2=1 C.l1﹣l2=2 D.l1﹣l2=4
7.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为n,宽为m)的盒子底部(如图②),盒子底部未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分周长和是( )
A. B. C. D.
8.如图,在一个大长方形中放入三个边长不等的小正方形①、②、③,若要求出两个阴影部分周长的差,只要知道下列哪个图形的面积( )
A.正方形① B.正方形② C.正方形③ D.大长方形
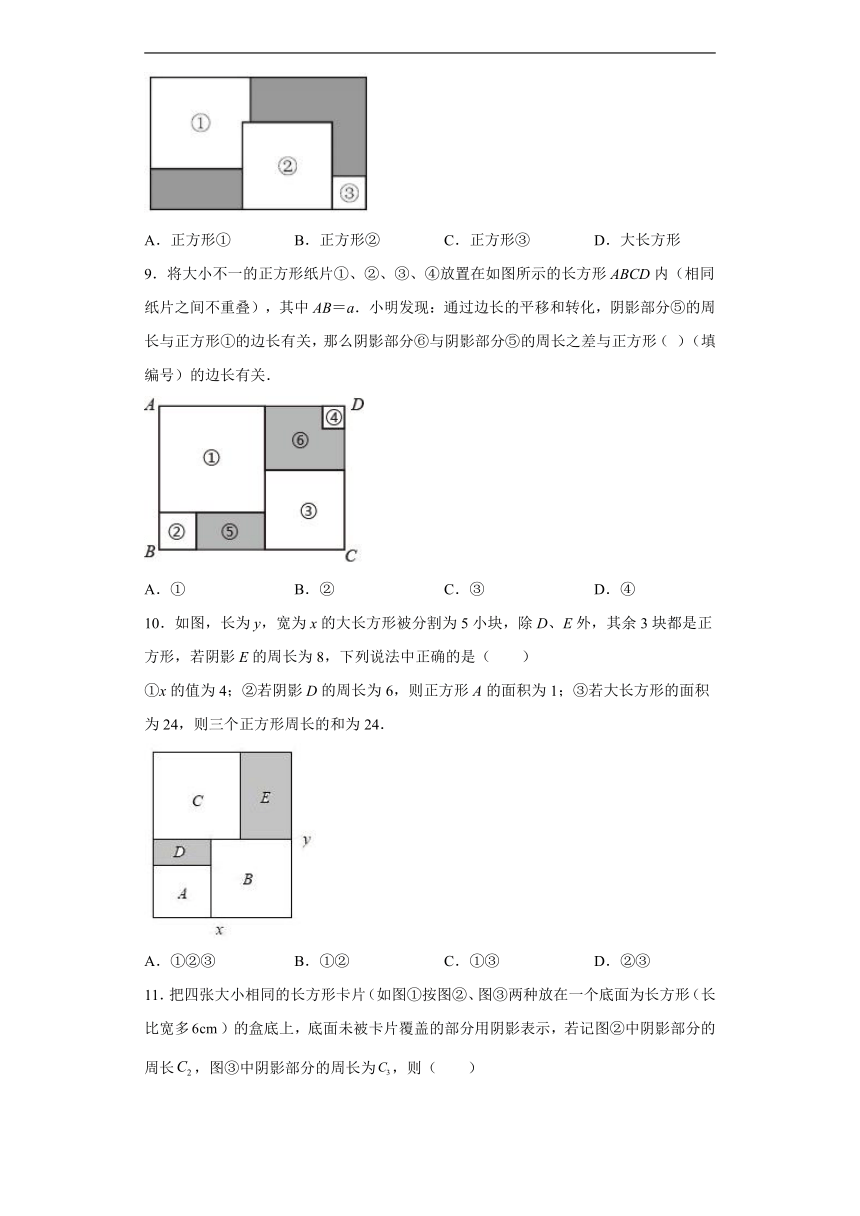
9.将大小不一的正方形纸片①、②、③、④放置在如图所示的长方形ABCD内(相同纸片之间不重叠),其中AB=a.小明发现:通过边长的平移和转化,阴影部分⑤的周长与正方形①的边长有关,那么阴影部分⑥与阴影部分⑤的周长之差与正方形( )(填编号)的边长有关.
A.① B.② C.③ D.④
10.如图,长为y,宽为x的大长方形被分割为5小块,除D、E外,其余3块都是正方形,若阴影E的周长为8,下列说法中正确的是( )
①x的值为4;②若阴影D的周长为6,则正方形A的面积为1;③若大长方形的面积为24,则三个正方形周长的和为24.
A.①②③ B.①② C.①③ D.②③
11.把四张大小相同的长方形卡片(如图①按图②、图③两种放在一个底面为长方形(长比宽多)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长,图③中阴影部分的周长为,则( )
A. B.比大 C.比小 D.比大
12.甲、乙两个油桶中装有体积相等的油.先把甲桶的油倒一半到乙桶(乙桶没有溢出),再把乙桶的油倒出给甲桶(甲桶没有溢出),这时两个油桶中的油的是( )
A.甲桶的油多
B.乙桶的油多
C.甲桶与乙桶一样多
D.无法判断,与原有的油的体积大小有关
二、填空题
13.某数学老师在课外活动中做了一个有趣的游戏:首先发给A、B、C三个同学相同数量的扑克牌假定发到每个同学手中的扑克牌数量足够多,然后依次完成以下三个步骤:
第一步,A同学拿出二张扑克牌给B同学;
第二步,C同学拿出三张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学.
请你确定,最终B同学手中剩余的扑克牌的张数为______.
14.若实数x,y,z满足,则代数式_______.
15.将图①中周长为36的长方形纸片剪成1号,2号,3号,4号正方形和5号长方形,并将它们按图②的方式放入周长为55的长方形中,则没有覆盖的阴影部分的周长为______.
16.如图,在长方形内有三块面积分别是的图形.则阴影部分的面积为______.
三、解答题
17.已知A、B为整式,A的表达式为3a2b﹣2ab2+abc,小明错将“C=2A﹣B”看成“2A+B”,算得结果C=4a2b﹣3ab2+4abc.
(1)求B的表达式;
(2)求正确的结果的表达式.
18.先化简,再求值:,其中.
19.先化简,再求值:,其中,.
20.先化简,再求值:,其中,.
21.先化简,再求值:,其中.
22.先化简,再求值:,其中.
23.先化简,再求值:,其中,.
24.已知.
(1)化简
(2)当,时,求的值.
25.化简求值:,其中,.
26.有长为米(米)的篱笆,利用它和房屋的一面墙(足够长)围成长方形园子,园子的宽为3米.
(1)若围成的园子如图1所示,求园子的面积(用含的代数式表示).
(2)若围成的园子如图2所示,在园子的中间用篱笆隔开,并在上面开一道1米宽的门,此时园子的面积与图1中园子的面积相比,是增大还是减小了?增大或减小了多少?
27.先化简,再求值:,其中,.
28.数学课上,老师设计了一个数学游戏:若两个多项式相减的结果等于第三个多项式,则称这三个多项式为“友好多项式”.甲、乙、丙、丁四位同学各有一张多项式卡片,下面是甲、乙、丙、丁四位同学的对话:
请根据对话解答下列问题:
甲:我的多项式是2x2-3x-2
乙:我的多项式是3x2-x+1
丙:我的多项式是x2+2x+3
丁:我和甲、乙两位同学的多项式是友好多项式
(1)判断甲、乙、丙三位同学的多项式是否为“友好多项式”,并说明理由.
(2)丁的多项式是什么?(请直接写出所有答案).
29.已知多项式M=(2x2+3xy+2y)﹣2(x2+x+yx+1).
(1)当x=1,y=2,求M的值;
(2)若多项式M与字母x的取值无关,求y的值.
30.定义;任意两个数a、b,按规则扩充得到一个新数c,称所得的新数c为“如意数”.
(1)若,直接写出a、b的“如意数”_______;
(2)若,求a、b的“如意数”c,并比较b与c的大小;
(3)已知,且a、b的“如意数”,则_______(用含x的式子表示).
参考答案
一、单选题
1.
【答案】A
【分析】
由题意得知:拼成的长方形的宽是(a+4)- (a+1),长是(a+4)+ (a+1),根据整式的加减运算法则,可得到结论.
【详解】
根据题意可得:
拼成的长方形的宽是:,
拼成的长方形的长是:
故选A.
【点睛】
此题考查了图形的剪拼,关键是根据题意列出式子,运用整式的加减运算法则进行计算.
2.
【答案】B
【分析】
根据相反数的定义以及整式的运算法则即可求出答案.
【详解】
解:由题意可知:a-4b=0,
∴原式=2b-4a+20+7a-14b-21
=3a-12b-1
=3(a-4b)-1
=-0-1
=-1,
故选:B.
【点睛】
本题考查整式的运算,解题的关键是熟练运用整式的运算,本题属于基础题型.
3.
【答案】B
【分析】
先根据题意列出进货的成本与销售额,再作差比较即可.
【详解】
解:由题意得,进货成本=30a+50b,销售额= ×(30+50),
×(30+50)-(30a+50b)
=40(a+b)-(30a+50b)
=40a+40b-30a-50b
=10(a-b),
∵b>a,
∴10(a-b)<0,
∴这家商店亏损了.
故选:B.
【点睛】
本题考查的是整式的加减,熟知整式的加减实质上就是合并同类项是解答此题的关键.
4.
【答案】C
【分析】
设重叠部分面积为c,(a-b)可理解为(a+c)-(b+c),即两个正方形面积的差.
【详解】
解:设重叠部分面积为c,
a-b
=(a+c)-(b+c)
=20-6
=14,
故选:C.
【点睛】
本题考查了等积变换,将阴影部分的面积之差转换成整个图形的面积之差是解题的关键.
5.
【答案】C
【分析】
可先求出两个图形中阴影部分的周长,观察到图②中的可得阴影部分的周长与长方形ABCD的周长相等,再根据长方形周长计算可求出l1,对于图③可设小卡片的宽为x,长为y,则有y+2x=m,再将两阴影部分的周长相加,通过合并同类项即可求解l2,因若,即可求m、n的关系式.
【详解】
解:图②中通过平移,可将阴影部分的周长转换为长为m,宽为n的长方形的周长,即图②中阴影部分的图形的周长l1为2m+2n
图③中,设小长形卡片的宽为x,长为y,则y+2x=m
所求的两个长方形的周长之各为:2m+2(n﹣y)+2(n﹣2x),
整理得,2m+4n﹣2m=4n
即l2为4n
∵,
∴2m+2n=×4n
整理得,m=n
故选:C.
【点睛】
此题主要通过长方形周长计算公式来考查整式加减的运算,灵活运用长方形周长计算公式即可解题.
6.
【答案】C
【分析】
观察图②可得阴影部分的周长与长方形的周长相等,可得l1=C1,观察图③可得阴影部分的周长与长方形的周长相等,可得l2=C2,若C1﹣C2=2,即可求l1,l2满足的关系式.
【详解】
解:观察图②可得阴影部分的周长与长方形的周长相等,可得l1=C1,
观察图③可得阴影部分的周长与长方形的周长相等,可得l2=C2,
∵C1﹣C2=2,
∴l1﹣l2=2.
故选:C.
【点睛】
此题考查整式的加减,关键是灵活运用长方形周长计算公式解题.
7.
【答案】B
【分析】
先设小长方形卡片的长为a,宽为b,再结合图形得出上面的阴影周长和下面的阴影周长,再把它们加起来即可求出答案.
【详解】
解:设小长方形卡片的长为a,宽为b,
∴L上面的阴影=2(n-a+m-a),
L下面的阴影=2(m-2b+n-2b),
∴L总的阴影=L上面的阴影+L下面的阴影=2(n-a+m-a)+2(m-2b+n-2b)=4m+4n-4(a+2b),
又∵a+2b=n,
∴4m+4n-4(a+2b)=4m.
故选:B.
【点睛】
本题主要考查了整式的加减运算,在解题时要根据题意结合图形得出答案是解题的关键.
8.
【答案】B
【分析】
如图,设三个正方形①②③的边长依次为a,b,c,重叠的小长方形的长和宽分别为x,y,表示出阴影部分的周长差即可求解.
【详解】
如图,设三个正方形①②③的边长依次为a,b,c,重叠的小长方形的长和宽分别为x,y,
∴阴影部分的周长差为2(a+b-x-c)+2(b+c-y)-2(b-x)-2(a-y)
=2a+2b-2x-2c+2b+2c-2y -2b+2x-2a+2y
=2b
故只要知道下列图形②的边长或面积即可求解,
故选B.
【点睛】
此题主要考查整式的加减、列代数式、去括号,解题的关键是根据图形的特点列出代数式求解.
9.
【答案】B
【分析】
通过边长的平移和转化,可得阴影部分⑥的周长=2a.设②的边长是m.用m,a表示出⑤的周长,进而即可解决问题.
【详解】
解:通过边长的平移和转化,可得阴影部分⑥的周长=2AB=2a.
设②的边长是m.
∴通过边长的平移和转化,阴影部分⑤的周长是2(a m),
∴阴影部分⑥ 阴影部分⑤=2a 2(a m)=2m.
阴影部分⑥与阴影部分⑤的周长之差与正方形②的边长有关,
故选B.
【点睛】
本题考查正方形的性质,矩形的性质等知识,解题的关键是通过边长的平移和转化,利用未知数表示阴影部分的周长.
10.
【答案】B
【分析】
设正方形A的边长为a, 正方形B的边长为b,正方形C的边长为c,表示出阴影E的长和宽,阴影D的长和宽,然后结合图形逐项分析即可.
【详解】
设正方形A的边长为a, 正方形B的边长为b,正方形C的边长为c,则x=a+b,y=b+c,阴影E的长为c,宽为a+b-c,阴影D的长为a,宽为b-a,
①∵阴影E的周长为8,
∴2(c+a+b-c)=8,
∴a+b=4,
即x=4,故①正确;
②∵阴影D的周长为6,
∴2(a+b-a)=6,
∴b=3,
∵a+b=4,
∴a=1,
∴正方形A的面积为1,故②正确;
③∵大长方形的面积为24,
∴xy=24,
∵x=4,
∴y=6,
∴b+c=6,
假设三个正方形周长的和为24,
则4a+4b+4c=24,
∴a+b+c=6,
∴a=0,不合题意,故③错误;
故选B.
【点睛】
本题考查了整式加减的应用,用a,b,c表示出x,y是解答本题的关键.
11.
【答案】B
【分析】
本题需先设小长方形的长为acm,宽为bcm,再结合图形分别得出图形②的阴影周长和图形③的阴影周长,比较后即可求出答案.
【详解】
解:设小长方形的长为acm,宽为bcm,大长方形的宽为xcm,长为(x+6)cm,
∴②阴影周长为:2(x+6+x)=4x+12;
∴③上面的阴影周长为:2(x-a+x+6-a),
下面的阴影周长为:2(x+6-2b+x-2b),
∴总周长为:2(x-a+x+6-a)+2(x+6-2b+x-2b)=4(x+6)+4x-4(a+2b),
又∵a+2b=x+6,
∴4(x+6)+4x-4(a+2b)=4x.
∴C2比C3大12cm.
故选:B.
【点睛】
本题主要考查了整式的加减运算,在解题时要根据题意结合图形得出答案是解题的关键.
12.
【答案】C
【分析】
根据题意列出代数式进行比较即可求解.
【详解】
解:设甲、乙两个油桶中水的重量为.根据题意,得:
因为先把甲桶的油倒一半至乙桶,
甲桶的油,乙桶的油,
再把乙桶的油倒出三分之一给甲桶,
所以甲桶有油,
乙桶有油,
所以甲乙两桶油一样多.
故选:C.
【点睛】
本题考查用代数式表示实际问题,理解已知条件是关键,用含有字母的式子表示实际问题是重点
二、填空题
13.
【答案】7
【分析】
本题是整式加减法的综合运用,设每人有牌x张,解答时依题意列出算式,求出答案.
【详解】
设每人有牌x张,B同学从A同学处拿来二张扑克牌,又从C同学处拿来三张扑克牌后,
则B同学有张牌,
A同学有张牌,
那么给A同学后B同学手中剩余的扑克牌的张数为:.
故答案为:7.
【点睛】
本题考查列代数式以及整式的加减,解题关键根据题目中所给的数量关系,建立数学模型,根据运算提示,找出相应的等量关系.
14.
【答案】2
【分析】
设,分别用k表示出x,y,z,再代入代数式化简即可.
【详解】
解:设,
∴,,,
∴
=
=2
故答案为:2.
【点睛】
本题考查了整式的加减运算,解题的关键是用k表示出x,y,z.
15.
【答案】46
【分析】
设1号正方形的边长为x,2号正方形的边长为y,则3号正方形的边长为x+y,4号正方形的边长为2x+y,5号长方形的长为3x+y,宽为y-x,根据图1中长方形的周长为36,求得x+y=,根据图2中长方形的周长为55,求得AB=,没有覆盖的阴影部分的周长为四边形ABCD的周长=2(AB+AD),计算即可得到答案.
【详解】
解:设1号正方形的边长为x,2号正方形的边长为y,
则3号正方形的边长为x+y,4号正方形的边长为2x+y,
5号长方形的长为3x+y,宽为yx,
由图1中长方形的周长为36,可得,y+2(x+y)+(2x+y)=18,
解得:x+y=,
如图,图2中长方形的周长为55,
∴AB+2(x+y)+2x+y+y-x=,
∴AB=,
根据题意得:没有覆盖的阴影部分的周长为四边形ABCD的周长,
∴2 (AB+AD)
=2(+x+y+2x+y+y-x)
=2()
=552(x+y)
=559
=46,
故答案为:46.
【点睛】
本题考查整式加减的应用,设出未知数,列代数式表示各线段进而解决问题是关键.
16.
【答案】97
【分析】
所求的影阴部分,恰好是三角形ABC与三角形CDE的公共部分,而面积为13,49,35这三块是长方形中没有被三角形ABC与三角形CDE盖住的部分.因此,△ABC面积+△CDE面积+(13+49+35)=长方形面积+阴影部分面积.而△ABC的底是长方形的长,高是长方形的宽;△CDE的底是长方形的宽,高是长方形的长.因此,三角形ABC面积与三角形CDE面积,都是长方形面积的一半.
【详解】
解:设长方形的面积为S,则S△CDE=S△ABC=S,
由图形可知,S+S阴影=S△CDE+S△ABC+13+49+35
S阴影=S+S+13+49+35-S=97
故答案为:97.
【点睛】
本题考查长方形面积、三角形面积的计算.本题明白所求的影阴部分,恰好是三角形ABC与三角形CDE的公共部分,而面积为13、49、35这三块是长方形中没有被三角形ABC与三角形CDE盖住的部分是解决本题的关键,从而根据S+S阴影=S△CDE+S△ABC+13+49+35建立等量关系求解.
三、解答题
17.
【答案】(1)﹣2a2b+ab2+2abc;(2)8a2b﹣5ab2.
【分析】
(1)根据题意可得B=C﹣2A,然后再代入表示表示C和A的整式,然后去括号,合并同类项即可;
(2)代入表示A、B的整式,然后去括号,合并同类项可得答案.
【详解】
解:(1)∵2A+B=C,
∴B=C﹣2A=4a2b﹣3ab2+4abc﹣2(3a2b﹣2ab2+abc)
=4a2b﹣3ab2+4abc﹣6a2b+4ab2﹣2abc
=﹣2a2b+ab2+2abc;
(2)C=2A﹣B=2(3a2b﹣2ab2+abc)﹣(﹣2a2b+ab2+2abc)
=6a2b﹣4ab2+2abc+2a2b﹣ab2﹣2abc
=8a2b﹣5ab2.
【点睛】
本题考查整式的加减运算,熟练掌握整体代入的思想方法及去括号、合并同类项等运算技能是解题关键.
18.
【答案】;-13.
【分析】
原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.
【详解】
解:
.
当时,原式.
【点睛】
本题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.
19.
【答案】;27
【分析】
先去括号,再合并同类项,然后将值代入计算即可.
【详解】
解:原式
当,时,
原式
.
【点睛】
本题考查整式的加减.去括号时,注意要正确运用去括号法则考虑括号内的符号是否变号.
20.
【答案】;
【分析】
整式的加减混合运算,去括号,然后合并同类项化简,最后代入求值即可.
【详解】
解:
当,时
原式
.
【点睛】
本题考查整式的加减运算,掌握运算法则正确化简计算是解题关键.
21.
【答案】;3
【分析】
利用去括号,合并同类项法则进行化简,再代入求值即可.
【详解】
解:原式
当时,
【点睛】
本题考查了整式的加减运算化简求值问题,掌握去括号法则和合并同类项法则是解题的关键.
22.
【答案】,-9
【分析】
整式的加减运算,先去括号,然后合并同类项化简,最后代入求值
【详解】
解:
=
当时,原式
【点睛】
本题考查整式的加减运算,掌握运算法则正确计算求解是关键
23.
【答案】,-16
【分析】
先去括号,再合并同类项,把字母的值代入计算即可.
【详解】
解:,
,
,
当,时,
原式.
【点睛】
本题考查了整式的化简求值,准确熟练的化简,代入值后的正确计算是解题关键.
24.
【答案】(1);(2)-26
【分析】
(1)将已知代入计算即可;
(2)将,代入(1)所求结果即可解答.
【详解】
解:(1),
;
(2)当时,
.
【点睛】
本题考查了整式的加减-化简求值:先去括号,然后合并同类项,再把满足条件的字母的值代入计算得到对应的整式的值.
25.
【答案】,11
【分析】
先去小括号,然后合并同类项进行计算即可,最后将,代入求值即可;
【详解】
解:原式
当,时,
原式
【点睛】
本题考查了整式的加减运算,属于比较热点一类的题目,要注意去括号时前面是符号时要改变符号;
26.
【答案】(1)园子的面积平方米;(2)面积减小了,减小了6平方米.
【分析】
(1)根据图示1可知园子的长为,宽为3,即可表示院子面积的代数式;
(2)根据图示2可知园子的长为,宽为3,即可表示院子面积的代数式,然后将此代数式与(1)中代数式相减即可得出结果;
【详解】
解:(1)由题意得:
图1中园子长为:(米),
∴图1中园子的面积:(平方米),
∴园子的面积平方米.
(2)由题意得:
图2中园子长为:(米),
∴图2中园子的面积:(平方米),
∴(平方米),
∴此时园子的面积比图1中园子的面积减小了6平方米.
【点睛】
本题考查了列代数式以及利用代入法求代数式的值,涉及到长方形的面积公式,正确读图是解题的关键;
27.
【答案】,1
【分析】
整式的加减计算,先去括号,合并同类项进行化简,然后代入求值即可.
【详解】
解:
当时
原式
【点睛】
本题考查整式的加减运算,掌握运算顺序和计算法则正确计算是解题关键.
28.
【答案】(1)是;见解析;(2)﹣x2﹣2x﹣3 或x2+2x+3或5x2﹣4x﹣1
【分析】
(1)根据定义计算两个多项式的差等于第三个多项式可作判断;
(2)分情况讨论:①丁的多项式=甲的多项式﹣乙的多项式或丁的多项式=乙的多项式﹣甲的多项式;②丁的多项式=甲的多项式+乙的多项式.
【详解】
解:(1)∵(3x2﹣x+1)﹣(2x2﹣3x﹣2),
=3x2﹣x+1﹣2x2+3x+2,
=x2+2x+3,
∴甲、乙、丙三位同学的多项式是“友好多项式”;
(2)∵甲、乙、丁三位同学的多项式是“友好多项式”,
∴分两种情况:
①(2x2﹣3x﹣2)﹣(3x2﹣x+1)或(3x2﹣x+1)﹣(2x2﹣3x﹣2),
(2x2﹣3x﹣2)﹣(3x2﹣x+1)
=2x2﹣3x﹣2﹣3x2+x﹣1
=﹣x2﹣2x﹣3
(3x2﹣x+1)﹣(2x2﹣3x﹣2)
=3x2﹣x+1﹣2x2+3x+2
=x2+2x+3,
②(3x2﹣x+1)+(2x2﹣3x﹣2),
=5x2﹣4x﹣1;
∴丁的多项式是﹣x2﹣2x﹣3 或x2+2x+3或5x2﹣4x﹣1.
【点睛】
本题考查了新定义“友好多项式”,熟练掌握整式的加减法则是本题的关键.
29.
【答案】(1);(2)2
【分析】
(1)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值;
(2)M化简的结果变形后,根据M与字母x的取值无关,确定出y的值即可.
【详解】
解:(1)M=2x2+3xy+2y﹣2x22x﹣2yx2
=xy2x+2y2,
当x,y=2时,
原式;
(2)∵M=xy2x+2y2=(y2)x+2y2,且M与字母x的取值无关,
∴y2=0,
解得:y=2.
【点睛】
此题考查了整式的加减,熟练掌握运算法则是解本题的关键.
30.
【答案】(1)5;(2)c=1-x2,b≥c;(3)-x3-3x2+3
【分析】
(1)将已知a、b的值直接代入c=a+b-ab即可;
(2)将已知a、b的值直接代入c=a+b-ab,利用作差法比较b、c的大小;
(3)将c、a的值代入c=a+b-ab即可求b.
【详解】
解:(1)将a=2,b=-3代入c=a+b-ab,
∴c=2-3+6=5;
(2)将a=2,b=x2+1代入c=a+b-ab,
∴c=2+x2+1-2(x2+1)=1-x2,
∵b-c=x2+1-1+x2=2x2≥0,
∴b≥c;
(3)由c=a+b-ab,a=2,
∴x3+3x2-1=2+b-2b=2-b,
∴b=-x3-3x2+3;
故答案为:-x3-3x2+3.
【点睛】
本题考查整式的运算;熟练掌握整式的加法与减法运算法则,代数式的求值方法是解题关键
一、单选题
1.如图,从边长为(a+4)的正方形纸片中剪去一个边长为(a+1)的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形ABCD(不重叠无缝隙),则AD,AB的长分别是( )
A.3,2a+5 B.5,2a+8 C.5,2a+3 D.3,2a+2
2.如果和互为相反数,那么多项式的值是( )
A.-3 B.-1 C.1 D.3
3.某水果商店在甲批发市场以每千克元的价格购进30千克的橘子,又在乙批发市场以每千克元()的价格购进同样的50千克橘子.如果以每千克元的价格全部卖出这种橘子,那么这家商店( )
A.盈利了 B.亏损了 C.不盈不亏 D.盈亏不能确定
4.如图,两个长方形的面积分别为20,6,两阴影部分的面积分别为a,b,且,则等于( )
A.6 B.7 C.14 D.16
5.把四张形状大小完全相同的小长方形卡片(如图①),分两种不同形式不重叠的放在一个底面长为m,宽为n的长方形盒子底部(如图②、图③),盒子底面未被卡片覆盖的部分用阴影表示,设图②中阴影部分图形的周长为l1,图③中两个阴影部分图形的周长和为l2,若,则m,n满足( )
A.m=n B.m=n C.m=n D.m=n
6.把六张形状大小完全相同的小长方形卡片(如图①),分两种不同形式不重叠的放在一个长方形盒子底部(如图②、图③),盒子底面未被卡片覆盖的部分用阴影表示,设图②是长方形盒子的周长为C1,阴影部分图形的周长为l1,图③中长方形盒子的周长为C2,阴影部分图形的周长为l2,若C1﹣C2=2,则l1,l2满足( )
A.l1=l2 B.l1﹣l2=1 C.l1﹣l2=2 D.l1﹣l2=4
7.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为n,宽为m)的盒子底部(如图②),盒子底部未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分周长和是( )
A. B. C. D.
8.如图,在一个大长方形中放入三个边长不等的小正方形①、②、③,若要求出两个阴影部分周长的差,只要知道下列哪个图形的面积( )
A.正方形① B.正方形② C.正方形③ D.大长方形
9.将大小不一的正方形纸片①、②、③、④放置在如图所示的长方形ABCD内(相同纸片之间不重叠),其中AB=a.小明发现:通过边长的平移和转化,阴影部分⑤的周长与正方形①的边长有关,那么阴影部分⑥与阴影部分⑤的周长之差与正方形( )(填编号)的边长有关.
A.① B.② C.③ D.④
10.如图,长为y,宽为x的大长方形被分割为5小块,除D、E外,其余3块都是正方形,若阴影E的周长为8,下列说法中正确的是( )
①x的值为4;②若阴影D的周长为6,则正方形A的面积为1;③若大长方形的面积为24,则三个正方形周长的和为24.
A.①②③ B.①② C.①③ D.②③
11.把四张大小相同的长方形卡片(如图①按图②、图③两种放在一个底面为长方形(长比宽多)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图②中阴影部分的周长,图③中阴影部分的周长为,则( )
A. B.比大 C.比小 D.比大
12.甲、乙两个油桶中装有体积相等的油.先把甲桶的油倒一半到乙桶(乙桶没有溢出),再把乙桶的油倒出给甲桶(甲桶没有溢出),这时两个油桶中的油的是( )
A.甲桶的油多
B.乙桶的油多
C.甲桶与乙桶一样多
D.无法判断,与原有的油的体积大小有关
二、填空题
13.某数学老师在课外活动中做了一个有趣的游戏:首先发给A、B、C三个同学相同数量的扑克牌假定发到每个同学手中的扑克牌数量足够多,然后依次完成以下三个步骤:
第一步,A同学拿出二张扑克牌给B同学;
第二步,C同学拿出三张扑克牌给B同学;
第三步,A同学手中此时有多少张扑克牌,B同学就拿出多少张扑克牌给A同学.
请你确定,最终B同学手中剩余的扑克牌的张数为______.
14.若实数x,y,z满足,则代数式_______.
15.将图①中周长为36的长方形纸片剪成1号,2号,3号,4号正方形和5号长方形,并将它们按图②的方式放入周长为55的长方形中,则没有覆盖的阴影部分的周长为______.
16.如图,在长方形内有三块面积分别是的图形.则阴影部分的面积为______.
三、解答题
17.已知A、B为整式,A的表达式为3a2b﹣2ab2+abc,小明错将“C=2A﹣B”看成“2A+B”,算得结果C=4a2b﹣3ab2+4abc.
(1)求B的表达式;
(2)求正确的结果的表达式.
18.先化简,再求值:,其中.
19.先化简,再求值:,其中,.
20.先化简,再求值:,其中,.
21.先化简,再求值:,其中.
22.先化简,再求值:,其中.
23.先化简,再求值:,其中,.
24.已知.
(1)化简
(2)当,时,求的值.
25.化简求值:,其中,.
26.有长为米(米)的篱笆,利用它和房屋的一面墙(足够长)围成长方形园子,园子的宽为3米.
(1)若围成的园子如图1所示,求园子的面积(用含的代数式表示).
(2)若围成的园子如图2所示,在园子的中间用篱笆隔开,并在上面开一道1米宽的门,此时园子的面积与图1中园子的面积相比,是增大还是减小了?增大或减小了多少?
27.先化简,再求值:,其中,.
28.数学课上,老师设计了一个数学游戏:若两个多项式相减的结果等于第三个多项式,则称这三个多项式为“友好多项式”.甲、乙、丙、丁四位同学各有一张多项式卡片,下面是甲、乙、丙、丁四位同学的对话:
请根据对话解答下列问题:
甲:我的多项式是2x2-3x-2
乙:我的多项式是3x2-x+1
丙:我的多项式是x2+2x+3
丁:我和甲、乙两位同学的多项式是友好多项式
(1)判断甲、乙、丙三位同学的多项式是否为“友好多项式”,并说明理由.
(2)丁的多项式是什么?(请直接写出所有答案).
29.已知多项式M=(2x2+3xy+2y)﹣2(x2+x+yx+1).
(1)当x=1,y=2,求M的值;
(2)若多项式M与字母x的取值无关,求y的值.
30.定义;任意两个数a、b,按规则扩充得到一个新数c,称所得的新数c为“如意数”.
(1)若,直接写出a、b的“如意数”_______;
(2)若,求a、b的“如意数”c,并比较b与c的大小;
(3)已知,且a、b的“如意数”,则_______(用含x的式子表示).
参考答案
一、单选题
1.
【答案】A
【分析】
由题意得知:拼成的长方形的宽是(a+4)- (a+1),长是(a+4)+ (a+1),根据整式的加减运算法则,可得到结论.
【详解】
根据题意可得:
拼成的长方形的宽是:,
拼成的长方形的长是:
故选A.
【点睛】
此题考查了图形的剪拼,关键是根据题意列出式子,运用整式的加减运算法则进行计算.
2.
【答案】B
【分析】
根据相反数的定义以及整式的运算法则即可求出答案.
【详解】
解:由题意可知:a-4b=0,
∴原式=2b-4a+20+7a-14b-21
=3a-12b-1
=3(a-4b)-1
=-0-1
=-1,
故选:B.
【点睛】
本题考查整式的运算,解题的关键是熟练运用整式的运算,本题属于基础题型.
3.
【答案】B
【分析】
先根据题意列出进货的成本与销售额,再作差比较即可.
【详解】
解:由题意得,进货成本=30a+50b,销售额= ×(30+50),
×(30+50)-(30a+50b)
=40(a+b)-(30a+50b)
=40a+40b-30a-50b
=10(a-b),
∵b>a,
∴10(a-b)<0,
∴这家商店亏损了.
故选:B.
【点睛】
本题考查的是整式的加减,熟知整式的加减实质上就是合并同类项是解答此题的关键.
4.
【答案】C
【分析】
设重叠部分面积为c,(a-b)可理解为(a+c)-(b+c),即两个正方形面积的差.
【详解】
解:设重叠部分面积为c,
a-b
=(a+c)-(b+c)
=20-6
=14,
故选:C.
【点睛】
本题考查了等积变换,将阴影部分的面积之差转换成整个图形的面积之差是解题的关键.
5.
【答案】C
【分析】
可先求出两个图形中阴影部分的周长,观察到图②中的可得阴影部分的周长与长方形ABCD的周长相等,再根据长方形周长计算可求出l1,对于图③可设小卡片的宽为x,长为y,则有y+2x=m,再将两阴影部分的周长相加,通过合并同类项即可求解l2,因若,即可求m、n的关系式.
【详解】
解:图②中通过平移,可将阴影部分的周长转换为长为m,宽为n的长方形的周长,即图②中阴影部分的图形的周长l1为2m+2n
图③中,设小长形卡片的宽为x,长为y,则y+2x=m
所求的两个长方形的周长之各为:2m+2(n﹣y)+2(n﹣2x),
整理得,2m+4n﹣2m=4n
即l2为4n
∵,
∴2m+2n=×4n
整理得,m=n
故选:C.
【点睛】
此题主要通过长方形周长计算公式来考查整式加减的运算,灵活运用长方形周长计算公式即可解题.
6.
【答案】C
【分析】
观察图②可得阴影部分的周长与长方形的周长相等,可得l1=C1,观察图③可得阴影部分的周长与长方形的周长相等,可得l2=C2,若C1﹣C2=2,即可求l1,l2满足的关系式.
【详解】
解:观察图②可得阴影部分的周长与长方形的周长相等,可得l1=C1,
观察图③可得阴影部分的周长与长方形的周长相等,可得l2=C2,
∵C1﹣C2=2,
∴l1﹣l2=2.
故选:C.
【点睛】
此题考查整式的加减,关键是灵活运用长方形周长计算公式解题.
7.
【答案】B
【分析】
先设小长方形卡片的长为a,宽为b,再结合图形得出上面的阴影周长和下面的阴影周长,再把它们加起来即可求出答案.
【详解】
解:设小长方形卡片的长为a,宽为b,
∴L上面的阴影=2(n-a+m-a),
L下面的阴影=2(m-2b+n-2b),
∴L总的阴影=L上面的阴影+L下面的阴影=2(n-a+m-a)+2(m-2b+n-2b)=4m+4n-4(a+2b),
又∵a+2b=n,
∴4m+4n-4(a+2b)=4m.
故选:B.
【点睛】
本题主要考查了整式的加减运算,在解题时要根据题意结合图形得出答案是解题的关键.
8.
【答案】B
【分析】
如图,设三个正方形①②③的边长依次为a,b,c,重叠的小长方形的长和宽分别为x,y,表示出阴影部分的周长差即可求解.
【详解】
如图,设三个正方形①②③的边长依次为a,b,c,重叠的小长方形的长和宽分别为x,y,
∴阴影部分的周长差为2(a+b-x-c)+2(b+c-y)-2(b-x)-2(a-y)
=2a+2b-2x-2c+2b+2c-2y -2b+2x-2a+2y
=2b
故只要知道下列图形②的边长或面积即可求解,
故选B.
【点睛】
此题主要考查整式的加减、列代数式、去括号,解题的关键是根据图形的特点列出代数式求解.
9.
【答案】B
【分析】
通过边长的平移和转化,可得阴影部分⑥的周长=2a.设②的边长是m.用m,a表示出⑤的周长,进而即可解决问题.
【详解】
解:通过边长的平移和转化,可得阴影部分⑥的周长=2AB=2a.
设②的边长是m.
∴通过边长的平移和转化,阴影部分⑤的周长是2(a m),
∴阴影部分⑥ 阴影部分⑤=2a 2(a m)=2m.
阴影部分⑥与阴影部分⑤的周长之差与正方形②的边长有关,
故选B.
【点睛】
本题考查正方形的性质,矩形的性质等知识,解题的关键是通过边长的平移和转化,利用未知数表示阴影部分的周长.
10.
【答案】B
【分析】
设正方形A的边长为a, 正方形B的边长为b,正方形C的边长为c,表示出阴影E的长和宽,阴影D的长和宽,然后结合图形逐项分析即可.
【详解】
设正方形A的边长为a, 正方形B的边长为b,正方形C的边长为c,则x=a+b,y=b+c,阴影E的长为c,宽为a+b-c,阴影D的长为a,宽为b-a,
①∵阴影E的周长为8,
∴2(c+a+b-c)=8,
∴a+b=4,
即x=4,故①正确;
②∵阴影D的周长为6,
∴2(a+b-a)=6,
∴b=3,
∵a+b=4,
∴a=1,
∴正方形A的面积为1,故②正确;
③∵大长方形的面积为24,
∴xy=24,
∵x=4,
∴y=6,
∴b+c=6,
假设三个正方形周长的和为24,
则4a+4b+4c=24,
∴a+b+c=6,
∴a=0,不合题意,故③错误;
故选B.
【点睛】
本题考查了整式加减的应用,用a,b,c表示出x,y是解答本题的关键.
11.
【答案】B
【分析】
本题需先设小长方形的长为acm,宽为bcm,再结合图形分别得出图形②的阴影周长和图形③的阴影周长,比较后即可求出答案.
【详解】
解:设小长方形的长为acm,宽为bcm,大长方形的宽为xcm,长为(x+6)cm,
∴②阴影周长为:2(x+6+x)=4x+12;
∴③上面的阴影周长为:2(x-a+x+6-a),
下面的阴影周长为:2(x+6-2b+x-2b),
∴总周长为:2(x-a+x+6-a)+2(x+6-2b+x-2b)=4(x+6)+4x-4(a+2b),
又∵a+2b=x+6,
∴4(x+6)+4x-4(a+2b)=4x.
∴C2比C3大12cm.
故选:B.
【点睛】
本题主要考查了整式的加减运算,在解题时要根据题意结合图形得出答案是解题的关键.
12.
【答案】C
【分析】
根据题意列出代数式进行比较即可求解.
【详解】
解:设甲、乙两个油桶中水的重量为.根据题意,得:
因为先把甲桶的油倒一半至乙桶,
甲桶的油,乙桶的油,
再把乙桶的油倒出三分之一给甲桶,
所以甲桶有油,
乙桶有油,
所以甲乙两桶油一样多.
故选:C.
【点睛】
本题考查用代数式表示实际问题,理解已知条件是关键,用含有字母的式子表示实际问题是重点
二、填空题
13.
【答案】7
【分析】
本题是整式加减法的综合运用,设每人有牌x张,解答时依题意列出算式,求出答案.
【详解】
设每人有牌x张,B同学从A同学处拿来二张扑克牌,又从C同学处拿来三张扑克牌后,
则B同学有张牌,
A同学有张牌,
那么给A同学后B同学手中剩余的扑克牌的张数为:.
故答案为:7.
【点睛】
本题考查列代数式以及整式的加减,解题关键根据题目中所给的数量关系,建立数学模型,根据运算提示,找出相应的等量关系.
14.
【答案】2
【分析】
设,分别用k表示出x,y,z,再代入代数式化简即可.
【详解】
解:设,
∴,,,
∴
=
=2
故答案为:2.
【点睛】
本题考查了整式的加减运算,解题的关键是用k表示出x,y,z.
15.
【答案】46
【分析】
设1号正方形的边长为x,2号正方形的边长为y,则3号正方形的边长为x+y,4号正方形的边长为2x+y,5号长方形的长为3x+y,宽为y-x,根据图1中长方形的周长为36,求得x+y=,根据图2中长方形的周长为55,求得AB=,没有覆盖的阴影部分的周长为四边形ABCD的周长=2(AB+AD),计算即可得到答案.
【详解】
解:设1号正方形的边长为x,2号正方形的边长为y,
则3号正方形的边长为x+y,4号正方形的边长为2x+y,
5号长方形的长为3x+y,宽为yx,
由图1中长方形的周长为36,可得,y+2(x+y)+(2x+y)=18,
解得:x+y=,
如图,图2中长方形的周长为55,
∴AB+2(x+y)+2x+y+y-x=,
∴AB=,
根据题意得:没有覆盖的阴影部分的周长为四边形ABCD的周长,
∴2 (AB+AD)
=2(+x+y+2x+y+y-x)
=2()
=552(x+y)
=559
=46,
故答案为:46.
【点睛】
本题考查整式加减的应用,设出未知数,列代数式表示各线段进而解决问题是关键.
16.
【答案】97
【分析】
所求的影阴部分,恰好是三角形ABC与三角形CDE的公共部分,而面积为13,49,35这三块是长方形中没有被三角形ABC与三角形CDE盖住的部分.因此,△ABC面积+△CDE面积+(13+49+35)=长方形面积+阴影部分面积.而△ABC的底是长方形的长,高是长方形的宽;△CDE的底是长方形的宽,高是长方形的长.因此,三角形ABC面积与三角形CDE面积,都是长方形面积的一半.
【详解】
解:设长方形的面积为S,则S△CDE=S△ABC=S,
由图形可知,S+S阴影=S△CDE+S△ABC+13+49+35
S阴影=S+S+13+49+35-S=97
故答案为:97.
【点睛】
本题考查长方形面积、三角形面积的计算.本题明白所求的影阴部分,恰好是三角形ABC与三角形CDE的公共部分,而面积为13、49、35这三块是长方形中没有被三角形ABC与三角形CDE盖住的部分是解决本题的关键,从而根据S+S阴影=S△CDE+S△ABC+13+49+35建立等量关系求解.
三、解答题
17.
【答案】(1)﹣2a2b+ab2+2abc;(2)8a2b﹣5ab2.
【分析】
(1)根据题意可得B=C﹣2A,然后再代入表示表示C和A的整式,然后去括号,合并同类项即可;
(2)代入表示A、B的整式,然后去括号,合并同类项可得答案.
【详解】
解:(1)∵2A+B=C,
∴B=C﹣2A=4a2b﹣3ab2+4abc﹣2(3a2b﹣2ab2+abc)
=4a2b﹣3ab2+4abc﹣6a2b+4ab2﹣2abc
=﹣2a2b+ab2+2abc;
(2)C=2A﹣B=2(3a2b﹣2ab2+abc)﹣(﹣2a2b+ab2+2abc)
=6a2b﹣4ab2+2abc+2a2b﹣ab2﹣2abc
=8a2b﹣5ab2.
【点睛】
本题考查整式的加减运算,熟练掌握整体代入的思想方法及去括号、合并同类项等运算技能是解题关键.
18.
【答案】;-13.
【分析】
原式去括号合并得到最简结果,把x与y的值代入计算即可求出值.
【详解】
解:
.
当时,原式.
【点睛】
本题考查了整式的加减-化简求值,熟练掌握运算法则是解本题的关键.
19.
【答案】;27
【分析】
先去括号,再合并同类项,然后将值代入计算即可.
【详解】
解:原式
当,时,
原式
.
【点睛】
本题考查整式的加减.去括号时,注意要正确运用去括号法则考虑括号内的符号是否变号.
20.
【答案】;
【分析】
整式的加减混合运算,去括号,然后合并同类项化简,最后代入求值即可.
【详解】
解:
当,时
原式
.
【点睛】
本题考查整式的加减运算,掌握运算法则正确化简计算是解题关键.
21.
【答案】;3
【分析】
利用去括号,合并同类项法则进行化简,再代入求值即可.
【详解】
解:原式
当时,
【点睛】
本题考查了整式的加减运算化简求值问题,掌握去括号法则和合并同类项法则是解题的关键.
22.
【答案】,-9
【分析】
整式的加减运算,先去括号,然后合并同类项化简,最后代入求值
【详解】
解:
=
当时,原式
【点睛】
本题考查整式的加减运算,掌握运算法则正确计算求解是关键
23.
【答案】,-16
【分析】
先去括号,再合并同类项,把字母的值代入计算即可.
【详解】
解:,
,
,
当,时,
原式.
【点睛】
本题考查了整式的化简求值,准确熟练的化简,代入值后的正确计算是解题关键.
24.
【答案】(1);(2)-26
【分析】
(1)将已知代入计算即可;
(2)将,代入(1)所求结果即可解答.
【详解】
解:(1),
;
(2)当时,
.
【点睛】
本题考查了整式的加减-化简求值:先去括号,然后合并同类项,再把满足条件的字母的值代入计算得到对应的整式的值.
25.
【答案】,11
【分析】
先去小括号,然后合并同类项进行计算即可,最后将,代入求值即可;
【详解】
解:原式
当,时,
原式
【点睛】
本题考查了整式的加减运算,属于比较热点一类的题目,要注意去括号时前面是符号时要改变符号;
26.
【答案】(1)园子的面积平方米;(2)面积减小了,减小了6平方米.
【分析】
(1)根据图示1可知园子的长为,宽为3,即可表示院子面积的代数式;
(2)根据图示2可知园子的长为,宽为3,即可表示院子面积的代数式,然后将此代数式与(1)中代数式相减即可得出结果;
【详解】
解:(1)由题意得:
图1中园子长为:(米),
∴图1中园子的面积:(平方米),
∴园子的面积平方米.
(2)由题意得:
图2中园子长为:(米),
∴图2中园子的面积:(平方米),
∴(平方米),
∴此时园子的面积比图1中园子的面积减小了6平方米.
【点睛】
本题考查了列代数式以及利用代入法求代数式的值,涉及到长方形的面积公式,正确读图是解题的关键;
27.
【答案】,1
【分析】
整式的加减计算,先去括号,合并同类项进行化简,然后代入求值即可.
【详解】
解:
当时
原式
【点睛】
本题考查整式的加减运算,掌握运算顺序和计算法则正确计算是解题关键.
28.
【答案】(1)是;见解析;(2)﹣x2﹣2x﹣3 或x2+2x+3或5x2﹣4x﹣1
【分析】
(1)根据定义计算两个多项式的差等于第三个多项式可作判断;
(2)分情况讨论:①丁的多项式=甲的多项式﹣乙的多项式或丁的多项式=乙的多项式﹣甲的多项式;②丁的多项式=甲的多项式+乙的多项式.
【详解】
解:(1)∵(3x2﹣x+1)﹣(2x2﹣3x﹣2),
=3x2﹣x+1﹣2x2+3x+2,
=x2+2x+3,
∴甲、乙、丙三位同学的多项式是“友好多项式”;
(2)∵甲、乙、丁三位同学的多项式是“友好多项式”,
∴分两种情况:
①(2x2﹣3x﹣2)﹣(3x2﹣x+1)或(3x2﹣x+1)﹣(2x2﹣3x﹣2),
(2x2﹣3x﹣2)﹣(3x2﹣x+1)
=2x2﹣3x﹣2﹣3x2+x﹣1
=﹣x2﹣2x﹣3
(3x2﹣x+1)﹣(2x2﹣3x﹣2)
=3x2﹣x+1﹣2x2+3x+2
=x2+2x+3,
②(3x2﹣x+1)+(2x2﹣3x﹣2),
=5x2﹣4x﹣1;
∴丁的多项式是﹣x2﹣2x﹣3 或x2+2x+3或5x2﹣4x﹣1.
【点睛】
本题考查了新定义“友好多项式”,熟练掌握整式的加减法则是本题的关键.
29.
【答案】(1);(2)2
【分析】
(1)原式去括号合并得到最简结果,把x与y的值代入计算即可求出值;
(2)M化简的结果变形后,根据M与字母x的取值无关,确定出y的值即可.
【详解】
解:(1)M=2x2+3xy+2y﹣2x22x﹣2yx2
=xy2x+2y2,
当x,y=2时,
原式;
(2)∵M=xy2x+2y2=(y2)x+2y2,且M与字母x的取值无关,
∴y2=0,
解得:y=2.
【点睛】
此题考查了整式的加减,熟练掌握运算法则是解本题的关键.
30.
【答案】(1)5;(2)c=1-x2,b≥c;(3)-x3-3x2+3
【分析】
(1)将已知a、b的值直接代入c=a+b-ab即可;
(2)将已知a、b的值直接代入c=a+b-ab,利用作差法比较b、c的大小;
(3)将c、a的值代入c=a+b-ab即可求b.
【详解】
解:(1)将a=2,b=-3代入c=a+b-ab,
∴c=2-3+6=5;
(2)将a=2,b=x2+1代入c=a+b-ab,
∴c=2+x2+1-2(x2+1)=1-x2,
∵b-c=x2+1-1+x2=2x2≥0,
∴b≥c;
(3)由c=a+b-ab,a=2,
∴x3+3x2-1=2+b-2b=2-b,
∴b=-x3-3x2+3;
故答案为:-x3-3x2+3.
【点睛】
本题考查整式的运算;熟练掌握整式的加法与减法运算法则,代数式的求值方法是解题关键
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
