第三章 圆的基本性质 单元测试卷 (含答案)2024-2025学年浙教版九年级上册数学
文档属性
| 名称 | 第三章 圆的基本性质 单元测试卷 (含答案)2024-2025学年浙教版九年级上册数学 |

|
|
| 格式 | docx | ||
| 文件大小 | 697.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-08-01 00:00:00 | ||
图片预览


文档简介
圆的基本性质单元测试卷
一、选择题(每题3分,共30分)
1.下列说法正确的是( )
A.三个点可以确定一个圆
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.长度相等的弧是等弧
2.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
第2题图 第3题图 第4题图
A.28° B.30° C.36° D.56°
3.如图,是的直径,是的切线,连接,若,则的大小为( )
A. B. C. D.
4.如图,OA,OC是⊙O的半径,点B在⊙O上,若AB∥OC,∠BCO=21°,则∠AOC的度数是( )
A.42° B.21° C.84° D.60°
5.如图,点,,在上,,过点作的切线交的延长线于点,则的大小为( )
A. B. C. D.
6.如图中,,以C为圆心,为半径的圆交于点D,则的度数为( )
第5题图 第6题图 第7题图
A. B. C. D.
7.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,半径OA交小圆于点D,若OD=3, = ,则劣弧AB的长是( )
A.2π B.3π C.4π D.6π
8. 如图,CD为⊙O直径,CD⊥AB于点F,AE⊥BC于E,AE过圆心O,且AO=1.则四边形BEOF的面积为( )
第8题图 第9题图 第10题图
A. B. C. D.
9.如图,△ABC内接于⊙O,DE,FG是⊙O的弦,AB=DE,FG=AC.下列结论:①DE+FG=BC;②+=;③∠DOE+∠FOG=∠BOC;④∠DEO+∠FGO=∠BAC.其中所有正确结论的序号是( )
A.①②③④ B.②③ C.②④ D.②③④
10.如图,在扇形中,平分交于点,点为半径上一动点.若,则阴影部分周长的最小值为( )
A. B. C. D.
二、填空题(每题4分,共24分)
11.在中,已知cm,cm,P是BC的中点,以点P为圆心,3cm为半径画☉P,则点A与☉P的位置关系是 .
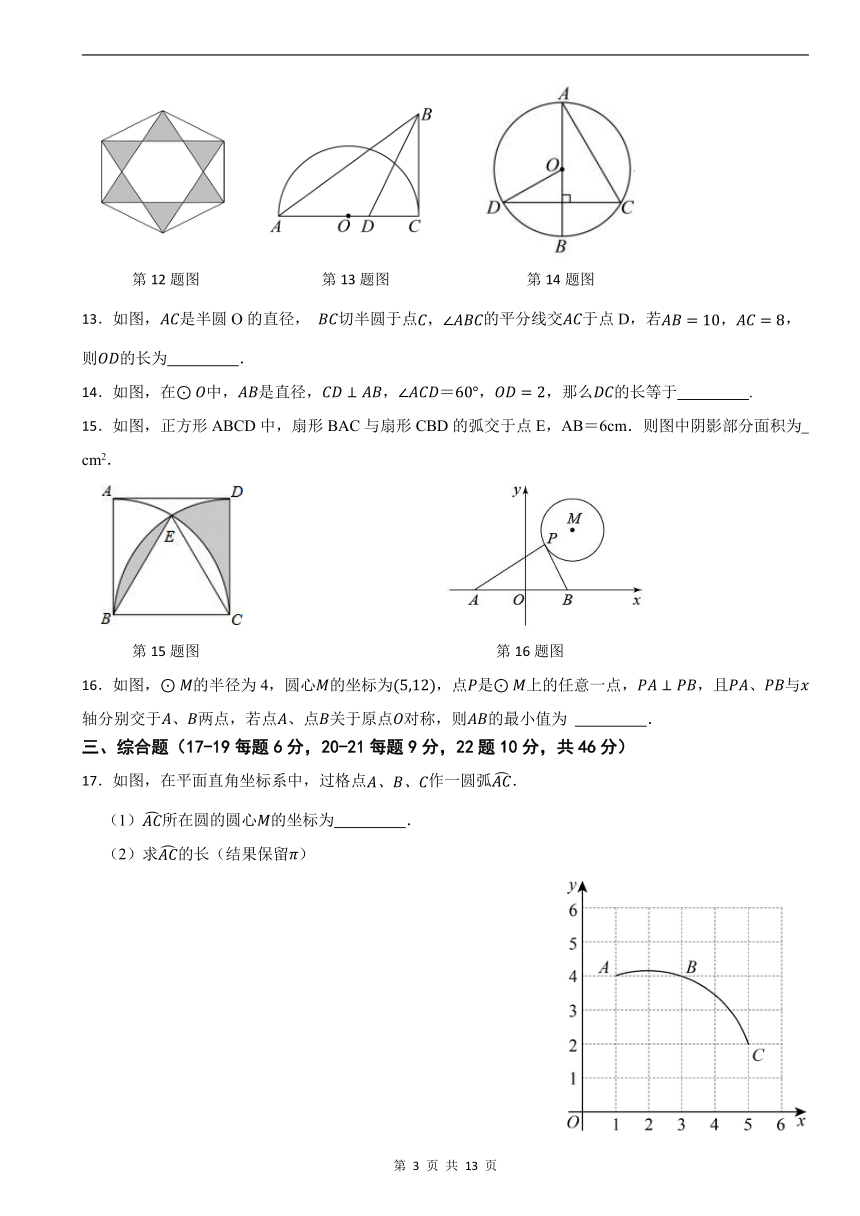
12.将一枚飞镖任意投掷到如图所示的正六边形镖盘上,若飞镖落在镖盘上各点的机会相等,则飞镖落在阴影区域的概率为 .
第12题图 第13题图 第14题图
13.如图,是半圆O的直径, 切半圆于点的平分线交于点D,若,则的长为 .
14.如图,在中,是直径,,=,,那么的长等于 .
15.如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=6cm.则图中阴影部分面积为 cm2.
第15题图 第16题图
16.如图,的半径为4,圆心的坐标为,点是上的任意一点,,且、与轴分别交于、两点,若点、点关于原点对称,则的最小值为 .
三、综合题(17-19每题6分,20-21每题9分,22题10分,共46分)
17.如图,在平面直角坐标系中,过格点作一圆弧.
(1)所在圆的圆心的坐标为 .
(2)求的长(结果保留)
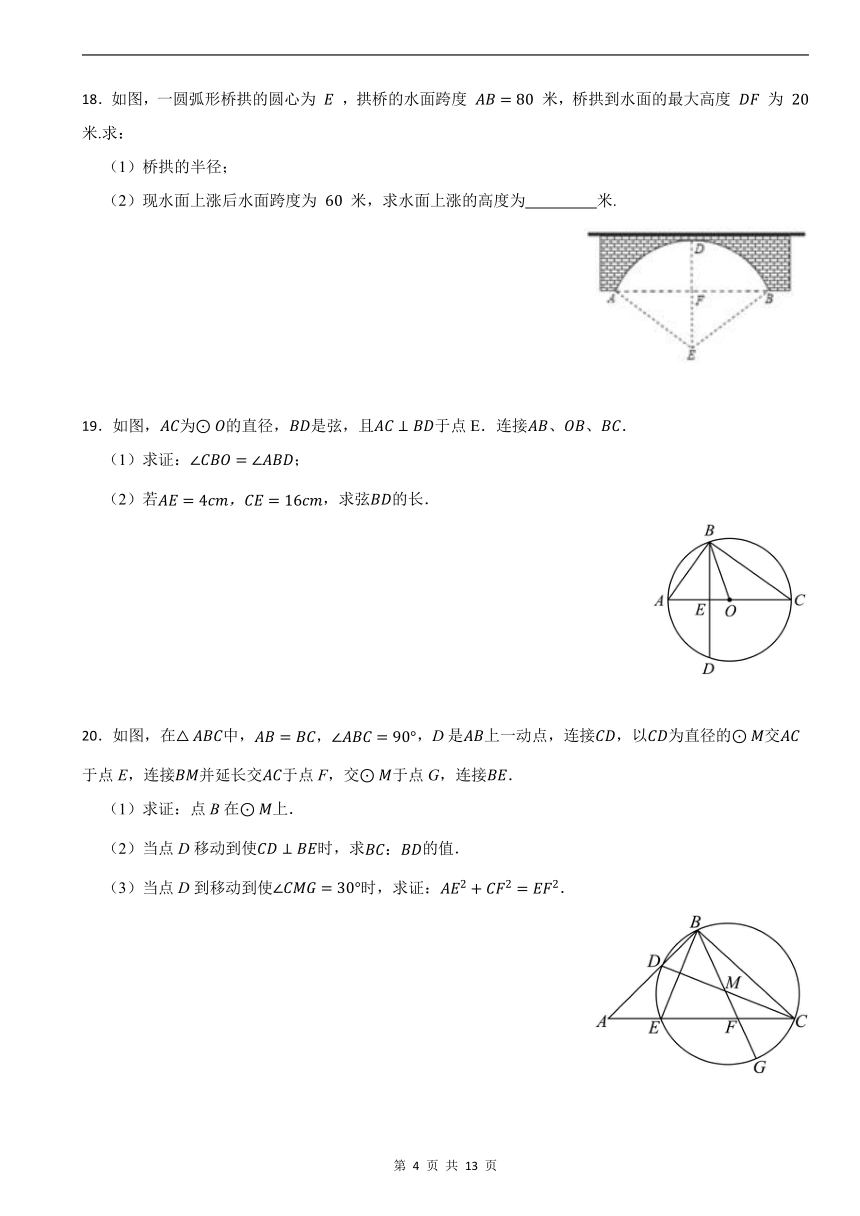
18.如图,一圆弧形桥拱的圆心为 ,拱桥的水面跨度 米,桥拱到水面的最大高度 为 米.求:
(1)桥拱的半径;
(2)现水面上涨后水面跨度为 米,求水面上涨的高度为 米.
19.如图,为的直径,是弦,且于点E.连接、、.
(1)求证:;
(2)若,求弦的长.
20.如图,在中,,D是上一动点,连接,以为直径的交于点E,连接并延长交于点F,交于点G,连接.
(1)求证:点B在上.
(2)当点D移动到使时,求的值.
(3)当点D到移动到使时,求证:.
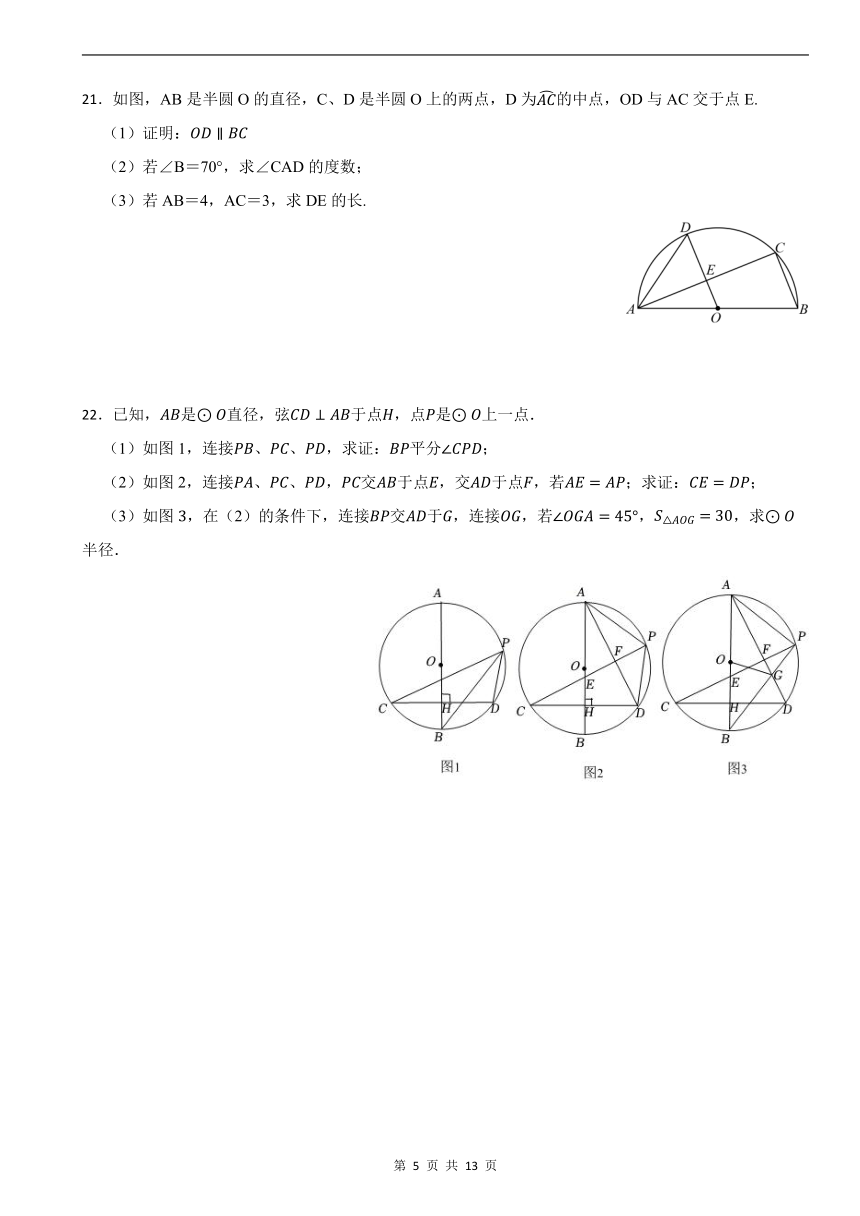
21.如图,AB是半圆O的直径,C、D是半圆O上的两点,D为的中点,OD与AC交于点E.
(1)证明:
(2)若∠B=70°,求∠CAD的度数;
(3)若AB=4,AC=3,求DE的长.
22.已知,是直径,弦于点,点是上一点.
(1)如图1,连接、、,求证:平分;
(2)如图2,连接、、,交于点,交于点,若;求证:;
(3)如图,在(2)的条件下,连接交于,连接,若,,求半径.
答案解析部分
1-5.【答案】BACAD
6-10.【答案】BCCDA
11.【答案】点A在圆P内
12.【答案】
13.【答案】
14.【答案】
15.【答案】3π
16.【答案】18
17.【答案】(1)
(2)解:连接MA、MC,如图所示:
,,
∴,
∴是等腰直角三角形,且,
所以的长:.
18.【答案】(1)如图,
设点E是拱桥所在的圆的圆心,作EF⊥AB于F,延长EF交圆于点D,
则由垂径定理知,点F是AB的中点,AF=FB= AB=40,EF=ED-FD=AE-DF,
由勾股定理知,AE2=AF2+EF2=AF2+(AE-DF)2,
设圆的半径是r,
则:r2=402+(r-20)2,
解得:r=50;
即桥拱的半径为50米;
(2)10
19.【答案】(1)证明:∵AC是直径,AC⊥BD
∴
∴∠ABD=∠C
又∵OB=OC
∴∠OBC=∠C
∴∠CBO=∠ABD
(2)解:∵AE=4cm,CE=16cm
∴直径AC=AE+CE=20cm
∴OA=OB=10cm
∴OE=OA-AE=10-4=6cm
∵AC是直径,AC⊥BD
∴BE=ED= cm
∴BD=2BE=16cm
20.【答案】(1)证明:根据题意得,
∵,
∴,
∴,
∴点B在上.
(2)解:连接,如图,
∵,为直径,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
(3)证明:过点B作,过点A作,交于点N,连接,
∵,
∴,
∴,
∵M为的中点,
∴,
∵,
∴,,,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
在中,,
∴.
21.【答案】(1)证明:∵D为的中点,
∴,
∴,
∵AB是直径,
∴∠ACB=90°,即BC⊥AC,
∴;
(2)解:如图所示,连接OC,
∵D为的中点,
∴OD⊥AC,,
∴
∵
∵∠AOD=∠B=70°,
∴;
(3)解:∵AB为直径,
∴∠ACB=90°,
∵AB=4,AC=3,
∴,OA=OD=2,
∵D为的中点,
∴AE=CE,
∵OA=OB,
∴,
∴.
22.【答案】(1)证明: 是 直径, ,
∴ ,
,
平分 ;
(2)证明:设 ,
,
,
,
,
,
,
,
∵ ,
,
,
,
,
,
,
,
如图2,连接 ,
,
∴△DFE≌△DFP(SAS) ,
,
, , ,
∴△CEH≌△DEH(ASA) ,
,
;
(3)解:如图3,连接 EG 、 CO ,
设 ,
为直径, ,
∴ ,
,由 知 ,
, ,
,
,
在 和 中,
,
∴△AFE≌△AFP(SAS) ,
,
,
∴AG为EP的中垂线,
,
,
∵AB为直径,
,
,
,
在 和 中,
, , ,
∴△AEG≌△APG(SSS) ,
,
, ,
,
,
,
,
,
,
设半径为 , ,
则 ,
∵ ,
,
,
,
,
,
,
在 和 中,
, , ,
∴△CHO≌△BGE(AAS) ,
,
,
,
,
,
在 中,由勾股定理得 ,
即 ,
,
,
则 ,
,
即 ,
令 ,
则原式为 ,
即 ,
解得: , 舍 ,
,
负值舍去 .
半径为10.
一、选择题(每题3分,共30分)
1.下列说法正确的是( )
A.三个点可以确定一个圆
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.长度相等的弧是等弧
2.将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为86°,30°,则∠ACB的度数是( )
第2题图 第3题图 第4题图
A.28° B.30° C.36° D.56°
3.如图,是的直径,是的切线,连接,若,则的大小为( )
A. B. C. D.
4.如图,OA,OC是⊙O的半径,点B在⊙O上,若AB∥OC,∠BCO=21°,则∠AOC的度数是( )
A.42° B.21° C.84° D.60°
5.如图,点,,在上,,过点作的切线交的延长线于点,则的大小为( )
A. B. C. D.
6.如图中,,以C为圆心,为半径的圆交于点D,则的度数为( )
第5题图 第6题图 第7题图
A. B. C. D.
7.如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点C,半径OA交小圆于点D,若OD=3, = ,则劣弧AB的长是( )
A.2π B.3π C.4π D.6π
8. 如图,CD为⊙O直径,CD⊥AB于点F,AE⊥BC于E,AE过圆心O,且AO=1.则四边形BEOF的面积为( )
第8题图 第9题图 第10题图
A. B. C. D.
9.如图,△ABC内接于⊙O,DE,FG是⊙O的弦,AB=DE,FG=AC.下列结论:①DE+FG=BC;②+=;③∠DOE+∠FOG=∠BOC;④∠DEO+∠FGO=∠BAC.其中所有正确结论的序号是( )
A.①②③④ B.②③ C.②④ D.②③④
10.如图,在扇形中,平分交于点,点为半径上一动点.若,则阴影部分周长的最小值为( )
A. B. C. D.
二、填空题(每题4分,共24分)
11.在中,已知cm,cm,P是BC的中点,以点P为圆心,3cm为半径画☉P,则点A与☉P的位置关系是 .
12.将一枚飞镖任意投掷到如图所示的正六边形镖盘上,若飞镖落在镖盘上各点的机会相等,则飞镖落在阴影区域的概率为 .
第12题图 第13题图 第14题图
13.如图,是半圆O的直径, 切半圆于点的平分线交于点D,若,则的长为 .
14.如图,在中,是直径,,=,,那么的长等于 .
15.如图,正方形ABCD中,扇形BAC与扇形CBD的弧交于点E,AB=6cm.则图中阴影部分面积为 cm2.
第15题图 第16题图
16.如图,的半径为4,圆心的坐标为,点是上的任意一点,,且、与轴分别交于、两点,若点、点关于原点对称,则的最小值为 .
三、综合题(17-19每题6分,20-21每题9分,22题10分,共46分)
17.如图,在平面直角坐标系中,过格点作一圆弧.
(1)所在圆的圆心的坐标为 .
(2)求的长(结果保留)
18.如图,一圆弧形桥拱的圆心为 ,拱桥的水面跨度 米,桥拱到水面的最大高度 为 米.求:
(1)桥拱的半径;
(2)现水面上涨后水面跨度为 米,求水面上涨的高度为 米.
19.如图,为的直径,是弦,且于点E.连接、、.
(1)求证:;
(2)若,求弦的长.
20.如图,在中,,D是上一动点,连接,以为直径的交于点E,连接并延长交于点F,交于点G,连接.
(1)求证:点B在上.
(2)当点D移动到使时,求的值.
(3)当点D到移动到使时,求证:.
21.如图,AB是半圆O的直径,C、D是半圆O上的两点,D为的中点,OD与AC交于点E.
(1)证明:
(2)若∠B=70°,求∠CAD的度数;
(3)若AB=4,AC=3,求DE的长.
22.已知,是直径,弦于点,点是上一点.
(1)如图1,连接、、,求证:平分;
(2)如图2,连接、、,交于点,交于点,若;求证:;
(3)如图,在(2)的条件下,连接交于,连接,若,,求半径.
答案解析部分
1-5.【答案】BACAD
6-10.【答案】BCCDA
11.【答案】点A在圆P内
12.【答案】
13.【答案】
14.【答案】
15.【答案】3π
16.【答案】18
17.【答案】(1)
(2)解:连接MA、MC,如图所示:
,,
∴,
∴是等腰直角三角形,且,
所以的长:.
18.【答案】(1)如图,
设点E是拱桥所在的圆的圆心,作EF⊥AB于F,延长EF交圆于点D,
则由垂径定理知,点F是AB的中点,AF=FB= AB=40,EF=ED-FD=AE-DF,
由勾股定理知,AE2=AF2+EF2=AF2+(AE-DF)2,
设圆的半径是r,
则:r2=402+(r-20)2,
解得:r=50;
即桥拱的半径为50米;
(2)10
19.【答案】(1)证明:∵AC是直径,AC⊥BD
∴
∴∠ABD=∠C
又∵OB=OC
∴∠OBC=∠C
∴∠CBO=∠ABD
(2)解:∵AE=4cm,CE=16cm
∴直径AC=AE+CE=20cm
∴OA=OB=10cm
∴OE=OA-AE=10-4=6cm
∵AC是直径,AC⊥BD
∴BE=ED= cm
∴BD=2BE=16cm
20.【答案】(1)证明:根据题意得,
∵,
∴,
∴,
∴点B在上.
(2)解:连接,如图,
∵,为直径,
∴,,
∵,
∴,
∴,
∴,
∴,
∴,
∴.
(3)证明:过点B作,过点A作,交于点N,连接,
∵,
∴,
∴,
∵M为的中点,
∴,
∵,
∴,,,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
在中,,
∴.
21.【答案】(1)证明:∵D为的中点,
∴,
∴,
∵AB是直径,
∴∠ACB=90°,即BC⊥AC,
∴;
(2)解:如图所示,连接OC,
∵D为的中点,
∴OD⊥AC,,
∴
∵
∵∠AOD=∠B=70°,
∴;
(3)解:∵AB为直径,
∴∠ACB=90°,
∵AB=4,AC=3,
∴,OA=OD=2,
∵D为的中点,
∴AE=CE,
∵OA=OB,
∴,
∴.
22.【答案】(1)证明: 是 直径, ,
∴ ,
,
平分 ;
(2)证明:设 ,
,
,
,
,
,
,
,
∵ ,
,
,
,
,
,
,
,
如图2,连接 ,
,
∴△DFE≌△DFP(SAS) ,
,
, , ,
∴△CEH≌△DEH(ASA) ,
,
;
(3)解:如图3,连接 EG 、 CO ,
设 ,
为直径, ,
∴ ,
,由 知 ,
, ,
,
,
在 和 中,
,
∴△AFE≌△AFP(SAS) ,
,
,
∴AG为EP的中垂线,
,
,
∵AB为直径,
,
,
,
在 和 中,
, , ,
∴△AEG≌△APG(SSS) ,
,
, ,
,
,
,
,
,
,
设半径为 , ,
则 ,
∵ ,
,
,
,
,
,
,
在 和 中,
, , ,
∴△CHO≌△BGE(AAS) ,
,
,
,
,
,
在 中,由勾股定理得 ,
即 ,
,
,
则 ,
,
即 ,
令 ,
则原式为 ,
即 ,
解得: , 舍 ,
,
负值舍去 .
半径为10.
同课章节目录
